4 Impuls

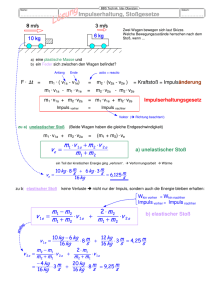
C Dynamik
4
-I.C9-
Impuls
4.1 Impuls und Kraftstoß
4.1.1 Impuls
Die Bewegung eines Körpers wird beispielsweise durch die
Geschwindigkeit beschrieben. Um die Bewegung eines Körpers
zu ändern braucht man eine Kraft (Abb.1). Diese führt zu einer
Änderung der Geschwindigkeit. Die neue Geschwindigkeit
hängt neben der Größe der Kraft auch von der Masse des
Körpers ab:
Um den Bewegungszustand eines Körpers zu beschreiben
verwendet man eine weitere Größe, den Impuls.
Abb.1: Geschwindigkeitsänderungen
beim Billiard
→
Der Impuls p kennzeichnet den
→
→
p =m⋅ v
Bewegungszustand eines Körpers.
Der Impuls ist eine vektorielle
Zustandsgröße.
→
p : Impuls
in Ns
m: Masse in kg
→
v : Geschwindigkeit in m/s
Beispiel:
Ein Meteorit mit der Masse 1 g dringt mit einer Geschwindigkeit von 30 km/s (Umlaufgeschwindigkeit der Erde
um die Sonne) in die Atmosphäre.
Die Geschwindigkeit eines PKWs von 1 t beträgt 110 km/h.
Berechne die kinetischen Energien und die Impulse der beiden Körper.
Lösung:
Sciences naturelles et technologie
I Mechanik
12GI
‘09
C Dynamik
4.1.2
-I.C10-
Kraftstoß
Liegt beim Billiard eine Kugel ruhig auf dem Tisch, hat sie den Impuls p = 0. Der Stoß mit der Queue verändert
den Impuls der Kugel. Der resultierende Impuls ist umso größer, je größer die wirkende Kraft ist und je länger
sie wirkt. Dies wird durch die physikalische Größe Kraftstoß beschrieben.
→
Der Kraftstoß S errechnet sich
aus der Dauer und der Größe einer
Kraftwirkung.
→
→
→
S = F ⋅ ∆t
S : Kraftstoß in Ns
→
F : Kraft in N
∆t: Dauer der Krafteinwirkung in s
Der Kraftstoß ist eine vektorielle
Prozessgröße.
Kraftstoß und Impuls werden in der gleichen Einheit gemessen. Der Impuls kennzeichnet den
Bewegungszustand eines Körpers. Der Kraftstoß beschreibt den Vorgang oder Prozess der Bewegungsänderung.
Der Kraftstoß ist gleich der erzielten Impulsänderung.
4.1.3 Impuls als Erhaltungsgröße
Kraftstöße und Impulsänderungen treten beispielsweise beim Rangieren von Eisenbahnwagen auf.
Betrachten wir zwei Kugeln 1 und 2 mit den Massen m1 bzw. m2 und den Geschwindigkeiten v1 bzw. v2, die
aufeinander prallen (Abb.2). Nach dem Aufprall sollen die Geschwindigkeiten u1 bzw. u2 betragen.
Abb.2: Aufprall von zwei Kugeln
→
→
Entsprechend dem Wechselwirkungsgesetz wirken gleich große, entgegen gesetzte Kräfte F1 und F2 beim
Prall. Die Dauer des Aufpralls ist für beide Kugeln gleich groß.
Es gilt für die Kraftstöße:
Daraus die Impulsänderung:
Man erkennt daß der Gesamtimpuls der Kugeln vor dem Stoß gleich dem Gesamtimpuls nach dem Stoß ist. Es
gilt das allgemein gültige Impulserhaltungsgesetz für mechanische Systeme:
n
Impulserhaltungssatz:
Ist bei einem System die Summe
aller von außen angreifenden Kräfte
gleich null, so ist die Vektorsumme
aller Impulse konstant.
Der
Impuls
Erhaltungsgröße.
ist
→
n
→
∑ m ⋅ vi = ∑ mi ⋅ui
1
1
mi:
Masse des Körpers i in kg
→
v i : Geschwindigkeit vor dem Stoß in m/s
→
u i : Geschwindigkeit nach dem Stoß in m/s
eine
Sciences naturelles et technologie
I Mechanik
12GI
‘09
C Dynamik
-I.C11-
4.2 Stoßprozesse
Stoßprozesse lassen sich nach der Art der Verformung und nach der Richtung, bezogen auf die
Bewegungsrichtung, unterscheiden.
- Bei der Verformung unterscheidet man die Grenzfälle elastischer und unelastischer Stoß:
Unelastische Stöße führen zu bleibenden Verformungen. Bsp.: Einschlagen eines Nagels, Schmieden von
Eisen.
Elastische Stöße treten nur elastische Verformungen auf. Bsp.: Ballspiele
- Die Richtung unterscheidet man zentrale und schiefe Stöße.
4.2.1 Zentraler unelastischer Stoß
Wenn die an einem Stoßvorgang beteiligten Körper unelastisch sind, verformen sie sich an der Berührungsstelle.
Sie bewegen sich dann mit gemeinsamer Geschwindigkeit weiter.
Für die Geschwindigkeiten nach dem Stoß gilt somit: u1 = u2 = u
Zur Vereinfachung wird zukünftig die Vektorschreibweise nicht mehr verwendet. Die Geschwindigkeiten und
Kräfte müssen entsprechend ihrem Richtungssinn mit dem richtigen Vorzeichen versehen werden.
Aus dem Impulserhaltungssatz folgt:
Geschwindigkeit nach dem zentralen unelastischen
Stoß:
u=
m1 ⋅ v1 + m 2 ⋅ v 2
m1 + m 2
Berechnung der kinetischen Energien:
Vor dem Stoß
Nach dem Stoß
Differenz der kinetischen Energien:
Erklärung: Ein Teil der kinetischen Energie wird in Verformungs- und
thermische Energie umgewandelt (Abb.3).
Die kinetische Energie bleibt beim unelastischen Stoß nicht erhalten.
Abb.3: Zentraler unelastischer Stoß
Sciences naturelles et technologie
I Mechanik
12GI
‘09
C Dynamik
4.2.2
-I.C12-
Schiefer unelastischer Stoß
(m1 + m2 ) u
Betrachten wir einen Skateboardfahrer, der schräg zur Fahrtrichtung auf
sein stehendes Brett aufspringt (Abb.4).
Der Impuls des Skaters kann vektoriell in eine Richtung senkrecht und
eine in Fahrtrichtung zerlegt werde. Die entsprechenden Beträge sind
m1 ⋅ vs = m1 ⋅ v ⋅ sinα und m1 ⋅ vp = m1 ⋅ v ⋅ cosα.
Beim Impuls senkrecht zur Fahrtrichtung handelt es sich um einen m1vp
zentralen unelastischen Stoß: das Skateboard kann sich nicht in diese
Richtung bewegen. Die Energie wird von den Gummirädern
aufgenommen.
Abb.4: Schiefer Stoß
m1v
α
m1vs
Der Impuls in Fahrtrichtung stellt ebenfalls einen zentralen unelastischen Stoß dar: Fahrer und Skateboard
bewegen sich gemeinsam mit gleicher Geschwindigkeit weiter.
Daher gilt:
Geschwindigkeit nach dem Aufspringen:
Anmerkung:
Die maximale Geschwindigkeit u erhält man bei α = 0°.
4.2.3
Zentraler elastischer Stoß
Beim zentralen elastischen Zusammenprall findet ein Energie- und Impulsaustausch statt
(Abb.5).
Beide Körper haben nach dem Stoß eine nach Betrag und Richtung veränderte
Geschwindigkeit.
Abb.5: Zentraler elastischer Stoß
Die Summe der kinetischen Energien vor und nach dem Stoß bleiben erhalten. Es gilt:
Aus dem Impulserhaltungssatz folgt:
Gleichung (1) geteilt durch (2):
Sciences naturelles et technologie
I Mechanik
12GI
‘09
C Dynamik
-I.C13-
Die Geschwindigkeit u2 eingesetzt in Gl.(2):
In gleicher Weise berechnet sich die Geschwindigkeit u2.
Geschwindigkeiten nach dem
zentralen elastischen Stoß:
4.2.4
u1 =
2 ⋅ m 2 ⋅ v 2 + (m 1 − m 2 ) ⋅ v 1
m1 + m 2
u2 =
2 ⋅ m 1 ⋅ v 1 + (m 2 − m 1 ) ⋅ v 2
m1 + m 2
Sonderfälle des elastischen Stoßes
Fall 1:
Die Massen der beiden Körper sind gleich groß. Ein Körper (z.B. Index 2) ruht vor dem Zusammenprall
(z.B. zwei Billiardkugeln).
Aus den Gleichungen im Abschnitt 4.2.3 ergibt sich:
Der ruhende Körper übernimmt die Geschwindigkeit des bewegten Körpers, dieser bleibt liegen.
Fall 2:
Die Masse des anfangs ruhenden Körpers (z.B. Index 2) ist sehr klein gegenüber dem bewegten Körper
(z.B. Aufschlag beim Tennis)
Aus den Gleichungen im Abschnitt 4.2.3 ergibt sich:
Der ruhende Körper erhält die doppelte Geschwindigkeit des bewegten Körpers, dieser verändert seine
Geschwindigkeit nicht.
Fall 3:
Die Masse des anfangs ruhenden Körpers (z.B. Index 2) ist viel größer als die des bewegten Körper
(z.B. Aufprall eines Balls gegen eine Wand)
Aus den Gleichungen im Abschnitt 4.2.3 ergibt sich:
Der Geschwindigkeit des bewegten Körpers bleibt erhalten, die Richtung ändert. Der ruhende Körper
bleibt unbewegt.
Sciences naturelles et technologie
I Mechanik
12GI
‘09
C Dynamik
-I.C14-
4.3 Aufgaben zu Stoßprozessen
Aufgabe 1:
Ein Güterwagen der Masse 3,2 t rollt mit 5 m/s unter der Ladevorrichtung durch, in der 10 t Steinkohle auf den
durchrollenden Wagen gekippt werden.
Welche Geschwindigkeit hat der Wagen nach dem Beladen?
Aufgabe 2:
Eine Kugel der Masse 1 g trifft auf einen Pendel der Masse 0,6 kg und prallt ab. Der Pendel schwingt aus und
erreicht eine maximale Höhe von 10 mm.
Welche Geschwindigkeit hatte die Kugel?
Aufgabe 3:
Eine Kugel der Masse 900 g trifft gerade mit 10 m/s gegen eine ruhende Kugel der Masse 10 kg.
Welche Geschwindigkeiten haben beide Kugeln nach einem elastischen Stoß? Berechne den exakten Wert und
berechne mit einer angenäherten Formel.
4.4 Aus Wissenschaft und Technik
Raketen:
Die Verbrennungsgase treten mit hoher Geschwindigkeit aus der Rakete (Abb.6),
aufgrund des Impulserhaltungssatzes bewegt sich die Rakete nach vorne. Da der durch
den Kraftstoß während der gesamten Brennzeit wirkt, ändert sich der Impuls der
Rakete permanent: die Geschwindigkeit nimmt kontinuierlich zu.
Oktopus:
Der Rückstoß-Antrieb der Rakete funktioniert auch im
Wasser. Viele Meerestiere (Quallen, Muscheln,
Tintenfische) nutzen ihn aus.
Der Oktopus beispielsweise (Abb.7) preßt bei Gefahr
blitzartig einen Wasserstrahl durch seinen Siphon und
kann dadurch schnell davon schwimmen.
Abb.7: Oktopus
Abb.6: Arian 6
Feuerwehrschlauch:
Je mehr Wasser in kurzer Zeit in den Brandherd kommt, desto schneller
kommt ein Feuer zum erliegen. Heutzutage pumpen Löschwagen
minütlich bis zu 3200 l Wasser mit ca. 25 m/s. Welche Gegenkraft ist bei
4 angeschlossenen Rohren pro Strahlrohr (Abb.8) erforderlich?
Abb.8: Feuerwehrschlauch
Sciences naturelles et technologie
I Mechanik
12GI
‘09