m v m v v m m m m m v v v m m m m

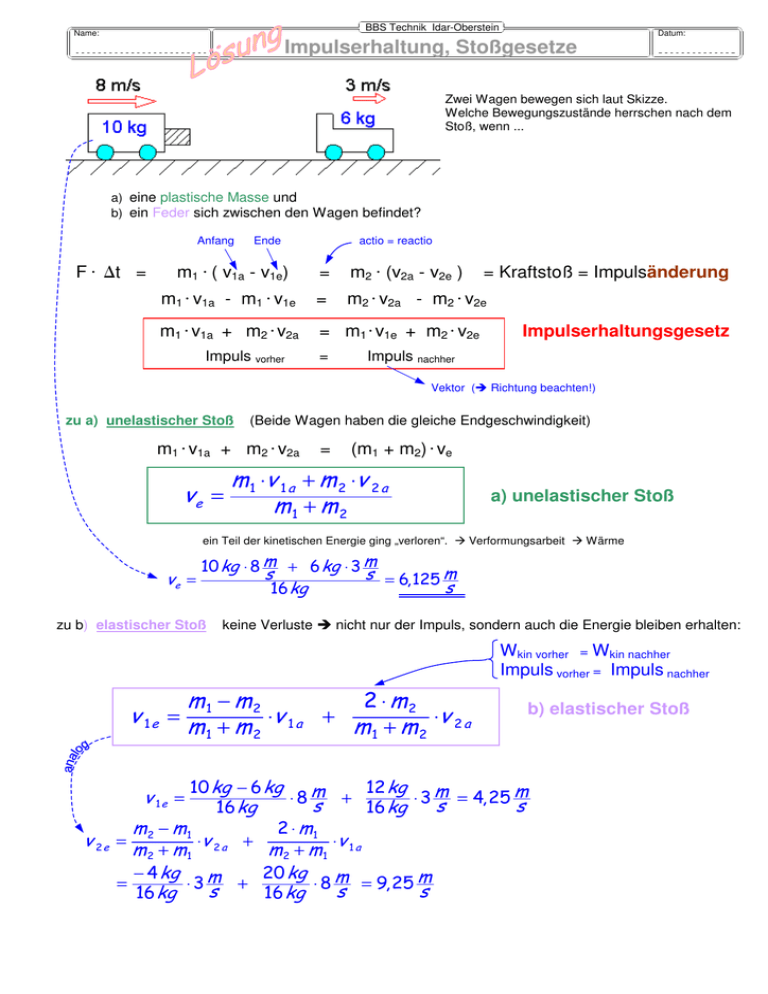
BBS Technik Idar-Oberstein
Name:
Datum:
Impulserhaltung, Stoßgesetze
Zwei Wagen bewegen sich laut Skizze.
Welche Bewegungszustände herrschen nach dem
Stoß, wenn ...
a) eine plastische Masse und
b) ein Feder sich zwischen den Wagen befindet?
Anfang
F ⋅ ∆t =
Ende
actio = reactio
m1 ⋅ ( v1a - v1e)
=
m2 ⋅ (v2a - v2e )
m1 ⋅ v1a - m1 ⋅ v1e
=
m2 ⋅ v2a - m2 ⋅ v2e
m1 ⋅ v1a + m2 ⋅ v2a
= m1 ⋅ v1e + m2 ⋅ v2e
Impuls vorher
=
= Kraftstoß = Impulsänderung
Impulserhaltungsgesetz
Impuls nachher
Vektor ( Richtung beachten!)
zu a) unelastischer Stoß
(Beide Wagen haben die gleiche Endgeschwindigkeit)
m1 ⋅ v1a + m2 ⋅ v2a
ve =
=
(m1 + m2) ⋅ ve
m 1 ⋅ v 1 a + m 2 ⋅v 2 a
m1 + m 2
a) unelastischer Stoß
ein Teil der kinetischen Energie ging „verloren“. Verformungsarbeit Wärme
ve =
10 kg ⋅ 8 m + 6 kg ⋅ 3 m
s
s = 6,125 m
s
16 kg
zu b) elastischer Stoß
keine Verluste nicht nur der Impuls, sondern auch die Energie bleiben erhalten:
Wkin vorher = Wkin nachher
Impuls vorher = Impuls nachher
v 1e
m1 − m 2
2 ⋅ m2
=
m 1 + m 2 ⋅v 1 a + m 1 + m 2 ⋅v 2 a
10 kg − 6 kg
12 kg
⋅8m +
⋅ 3 m = 4,25 m
s
s
s
16 kg
16 kg
m − m1
2 ⋅ m1
= 2
⋅v 2 a +
m 2 + m1
m 2 + m 1 ⋅v 1 a
− 4 kg m
20 kg
=
⋅3
+
⋅ 8 m = 9,25 m
s
s
s
16 kg
16 kg
v 1e =
v 2e
b) elastischer Stoß
BBS Technik Idar-Oberstein
Name:
Impulserhaltung, Stoßgesetze
Datum:
Exkurs:
Herleitung der Formel für den elastischen Stoß
Keine bleibende Verformung Bewegungsenergie bleibt erhalten:
m 1 ⋅v 1 a
Impulserhaltung
+ m 2 ⋅v 2 a = m 1 ⋅v 1 e + m 2 ⋅v 2 e
und
Energieerhaltung
1 m ⋅v
2 1
+ 1 m 2 ⋅v22a = 1 m 1 ⋅v12e + 1 m 2 ⋅v 22e
2
2
2
2
2
2
m 1 ⋅ (v1 a − v1 e ) = m 2 ⋅ (v 2 e − v 22a )
2
1a
m 1 ⋅ (v 1 a − v 1 e ) = m 2 ⋅ (v 2 e − v 2 a )
m 1 ⋅ (v12a − v12e ) m 2 ⋅ (v22e − v22a )
=
m 1 ⋅ (v 1 a − v 1 e ) m 2 ⋅ (v 2 e − v 2 a )
3. Binom:
a 2 −b 2 =(a+b)(a−b)
⋅
⇒
(v1 a + v1 e ) ⋅ (v1 a − v1 e ) (v 2 e + v 2 a ) ⋅ (v 2 e − v 2 a )
=
(v 1 a − v 1 e )
(v 2 e − v 2 a )
(v1 a + v1 e ) = (v 2 e + v 2 a )
v 2 e = v1 a + v1 e − v 2 a
m 1 ⋅ (v 1 a − v 1 e ) = m 2 ⋅ (v1 a + v1 e − v 2 a − v 2 a )
= m 2 ⋅ (v1 a + v1 e − 2 ⋅v 2 a )
m 1 ⋅v 1 a − m 2 ⋅v 1 a + 2 ⋅ m 2 ⋅v 2 a = m 1 ⋅v 1 e + m 2 ⋅v 1 e
v 1 a ⋅ (m 1 − m 2) + 2 ⋅ m 2 ⋅v 2 a = v 1 e ⋅ (m 1 + m 2)
m −m
2⋅m
v 1 e = m 1 + m 2 ⋅v 1 a + m + m2 ⋅v 2 a
1
2
1
2
BBS Technik Idar-Oberstein
Name:
Datum:
Impulserhaltung, Stoßgesetze 2
1. Zwei unterschiedlich große Massen (2 kg, 5 kg) haben zufällig den gleichen Impuls
Haben sie dann auch die gleiche kinetische Energien?.
Da m1 ⋅ v1 = m2 ⋅ v2 , so hat die kleinere Masse eine entsprechend höhere Geschwindigkeit. Bei der
kin. Energie wirkt sich aber die Geschwindigkeit quadratisch aus, d.h. die kleinere Masse hat die
höhere Energie.
m
m
z .B . : m 1 sei x2
⇒ v 1 = x ⋅v 2
denn : m1 ⋅v1 = x2 ⋅ x ⋅v 2
m
m
m
m
Wkin 1 = 1 ⋅v12 = 2 ⋅ (x ⋅v 2)2 = 2 ⋅ x 2 ⋅v 22 = x ⋅ 2 ⋅v 22 = x ⋅Wkin 2
2
2⋅x
2⋅x
2
(
2.
)
Ein Wagen mit der Gesamtmasse von 100 kg bewegt sich laut Skizze mit
gleich bleibender Geschwindigkeit von 4 m/s. Ein zweiter Wagen bewegt
sich mit 12 m/s dem ersten entgegen. Unmittelbar nach dem Stoß sind
beide Wagen in Ruhe.
a) Begründe, warum die Massen unterschiedlich sein müssen!
33,3 kg
b) Berechne die träge Masse m2 .
Da beide Massen ihren Impuls vollständig verlieren, müssen die Impulse (entgegengesetzt) gleich
groß gewesen sein.
m1 ⋅v1 + m2 ⋅ (−v 2) = 0
⇒ m1 ⋅v 1 = m2 ⋅v 2
Da v 2 > v1 ist , muss m2 < m1 sein .
m
m ⋅v 100 kg ⋅ 4 s
m2 = v1 1 =
= 33,3 kg
2
12 m
s
3. Ein Eisenbahnwaggon von 8 t rollt beim Rangieren
eine 60 cm hohe Gefällstrecke herab und stößt dann
laut Skizze (verlustfrei) gegen ein Hindernis.
a) Welche max. Kraft entsteht in jeder der beiden Federn mit D = 48000 N/cm?
480 kN
b) Wie groß ist der Kraftstoß auf das Hindernis?
c) Wie ändern sich die Ergebnis von a) und b), wenn Federn mit 24000 N/cm verwendet werden?
a) geg.: m = 8000 kg
h = 0,6 m
D = 48 000 N/cm
= 4 800 000 N/m
ges.: Fmax in N
Energiebilanz : WPot = 2 ⋅WSpann
m ⋅ g ⋅ h = 2 ⋅ 1 Fmax ⋅ s
2
F2
m ⋅ g ⋅ h = 2 ⋅ 1 ⋅ max
2 D
D = Fs
m
Fmax = D ⋅ m ⋅ g ⋅ h = 4 800 000 N
m ⋅ 8000 kg ⋅ 10 s 2 ⋅ 0, 6 m
Fmax = 480 kN
b)
F ⋅ ∆t = m ⋅ ∆v
F ⋅ ∆t = m ⋅v
ve = 0
v aus kin . Energie :
1 m ⋅v 2 = m ⋅ g ⋅ h
2
m
v = 2 ⋅ g ⋅ h = 2 ⋅ 10 m
s ⋅ 0, 6 m = 3, 45 s
m
F ⋅ ∆t = 8 000 kg ⋅ 3, 45 m
oder Ns
s = 27 712 kg s
Hinweis für physikalisch-technisch Sensible: Da sich die Feder wieder entspannt, ist der Kraftstoß größer als
errechnet (∆v ist größer). Wären die Reibungsverluste Null, dann wäre der Kraftstoß doppelt so groß wie errechnet
und der Waggon rollte wieder den Berg hoch. ;-)
c) Bei Verwendung einer weicheren Feder verringert sich die max. Kraft (um den Faktor 2 ,
Der Kraftstoß ändert sich nicht. (Die Zeit ∆t wird größer, aber m⋅v bleibt unverändert.)
s. 3a)
BBS Technik Idar-Oberstein
Name:
Datum:
Impulserhaltung, Stoßgesetze 2
4.
Zwei zylindrische Körper von m1 = 120 g und m2 = 300 g werden
durch eine plötzlich sich entspannender Feder in entgegen
gesetzter Richtung aus dem Lauf geworfen.
Mit welcher Geschwindigkeit werden sie davon geschleudert, wenn die Feder eine Spannenergie von
7,72 m/s 3.09 m/s
5 Nm abgibt?
geg.: m1 = 0,12 kg
m2 = 0,3 kg
WSpann = 5 Nm
ges.: v1 und v2 in m/s
1 Impulserhaltung: 0 = m1⋅(-v1) + m2⋅v2
m 1 ⋅v 2
v1 = m
2
2 Energieerhaltung: WSpann = ½ ⋅ m1 ⋅ v12 + ½ ⋅ m2 ⋅ v22
2
m
WSpann = 1 m1 22 ⋅v22 + 1 m2 ⋅v22
2 m1
2
2 ⋅WSpann
=
v2 = 2 ⋅ g ⋅ h =
m22
+
m
2
m1
kg ⋅ m
10
m
s2
= 3, 086 m
v2 =
s
1, 05 kg
 m2

= 1 ⋅v22 ⋅  2 + m2 
2
 m1

2 ⋅ 5 Nm
0, 09 kg + 0,3 kg
0,12
⇒ v1 =
m
m2 ⋅v2 0,3 kg ⋅ 3, 086 s
=
= 7, 715 m
m1
s
0,12 kg
5. Eine Masse m1 = 2 kg trifft mit der Geschwindigkeit von 3 m/s unelastisch auf eine ruhende zweite
Masse von m2 = 8 kg.
a) Welche Endgeschwindigkeit entsteht und
0,6 m/s
b) welcher Bruchteil der anfänglichen kinetischen Energie wird in Form von Formänderungsarbeit
in Wärme „verwandelt“?
80 %
a) geg.: m1 = 2 kg
v1a = 3 m/s
m2 = 8 kg
v2a = 0 m/s
ges.: ve in m/s
Verlust in %
b)
m1 ⋅ v1a + m2 ⋅ v2a = (m1 + m2)⋅ve
=0
2 kg ⋅ 3 m
m ⋅v
s = 0, 6 m
ve = m 1+ m1a =
s
10 kg
1
2
2
= 1 2 kg ⋅ 9 m2 = 9 Nm
2
2
s
2
2
1
Wkin nachher = (m 1 + m 2) ⋅ve
= 1 ⋅ 10 kg ⋅ 0,36 m2 = 1,8 Nm
2
2
s
⇒ Differenz = Wärme = 9 Nm − 1, 8 Nm = 7,2 Nm
Wkin vorher = 1 m 1 ⋅v12a
⇒ Wärme =
Wvorher
7,2 Nm
= 0,8 = 80%
9 Nm
6. Ein Auto (m1 = 1,6 t) soll ein anderes (m2 = 0,9 t) abschleppen.
Welche Geschwindigkeiten treten nach dem Ruck auf, der entsteht, wenn das ziehende Auto beim
Straffen des elastischen Abschleppseiles die Geschwindigkeit von 0,8 m/s besitzt? 0,224 m/s 1,024 m/s
geg.: m1 = 1,6 t
v1a = 0,8 m/s
m2 = 0,9 t
v2a = 0 m/s
ges.: v1e und v1e in m/s
m −m
2⋅m
v 1 e = m 1 + m 2 ⋅v 1 a + m + m2 ⋅v 2 a
1
2
1
2
=0
v 1e
1, 6t − 0, 9t
=
⋅ 0,8 m = 0,224 m
s
s
1, 6t + 0, 9t
Impulserhaltung: m1⋅v1a = m1⋅v1e + m2⋅v2e
m
m1 ⋅ (v 1a − v 1e ) 1, 6t ⋅ (0, 8 m
s − 0,224 s )
=
m2
0, 9t
m
= 1, 024
s
v 2e =
v 2e
BBS Technik Idar-Oberstein
Name:
Datum:
Impulserhaltung, Stoßgesetze 2
7. Ballistisches Pendel:
Um die Geschwindigkeit eines Geschosses (m1 = 12 g) zu bestimmen,
wird dieses in eine pendelnd aufgehängte Sandkiste (m2 = 20 kg)
geschossen, die dadurch um h = 2 cm angehoben wird.
1055 m/s
Welche Geschwindigkeit hatte das Geschoss?
geg.: m1 = 0,012 kg
m2 = 20 kg
h = 0,02 m
ges.: v1a in m/s
Impulserhaltung:
m1⋅v1a = (m1 + m2 ) ⋅ ve
= aus W kin = W pot
v 1a
1 (m + m ) ⋅v 2 = (m + m ) ⋅ g ⋅ h
2
1
2
e
2 1
m
ve = 2 ⋅ g ⋅ h (= 0,63 s )
(m + m 2)
20, 012 kg
= 1
⋅ 2 ⋅ g ⋅h =
⋅ 2 ⋅ 10 m2 ⋅ 0, 02 m
m1
0, 012 kg
s
v 1 a = 1055 m
s
8.
Begründe, warum α1 = α2 sein muss.
Da die Geschwindigkeit ein Vektor ist, ist auch der Impuls ein Vektor.
Somit kann man seine Komponenten getrennt betrachten: Beim Stoß kehrt
sich nur der senkrecht zur Wand wirkend Impuls um (s. Skizze). Deshalb
bleiben die Winkelverhältnisse gleich: α1 = α2 .
9. Ein Tennisball und ein Tonklumpen haben beide die gleiche Masse und werden mit der gleichen
Geschwindigkeit gegen die Wand geworfen.
Begründe, warum der Kraftstoß auf die Wand dennoch unterschiedlich ist.
Beide Massen haben am Anfang den gleichen Impuls.
Der Tonklumpen verliert den Impuls vollständig, weil am Ende seine Geschwindigkeit gleich bleibt.
P = m⋅∆v = F⋅∆t = I
Kraftstoß I ist hier = m⋅v
Der Tennisball verliert den Impuls (kurzzeitig) vollständig, wird aber sofort (durch die
Spannenergie) in die rückwärtige Bewegung beschleunigt.
Kraftstoß I ist hier = m⋅2v
10. Kreuze die richtigen Antworten an.
Der Impuls hat die gleiche Einheit wie der Kraftstoß.
Auch beim elastischen Stoß bleibt die Summe der Impulse konstant.
Der Impuls eines Körpers ist immer so groß wie der Kraftstoß während des Zusammentreffens.
Beim unelastischen Stoß entsteht Wärme.
Beim elastischen Stoß ist die Kraft während der Berührung konstant.
Impuls und Kraftstoß sind durch das Grundgesetz der Mechanik erklärbar.
Zusätzliche Infos, Beispiele, Aufgaben, Videos:
http://leifi.physik.uni-muenchen.de/web_ph11/materialseiten/m05_erhaltungssatz.htm