Harmonischer Mittelwert (Harmonisches Mittel) - Paul-Ehrlich

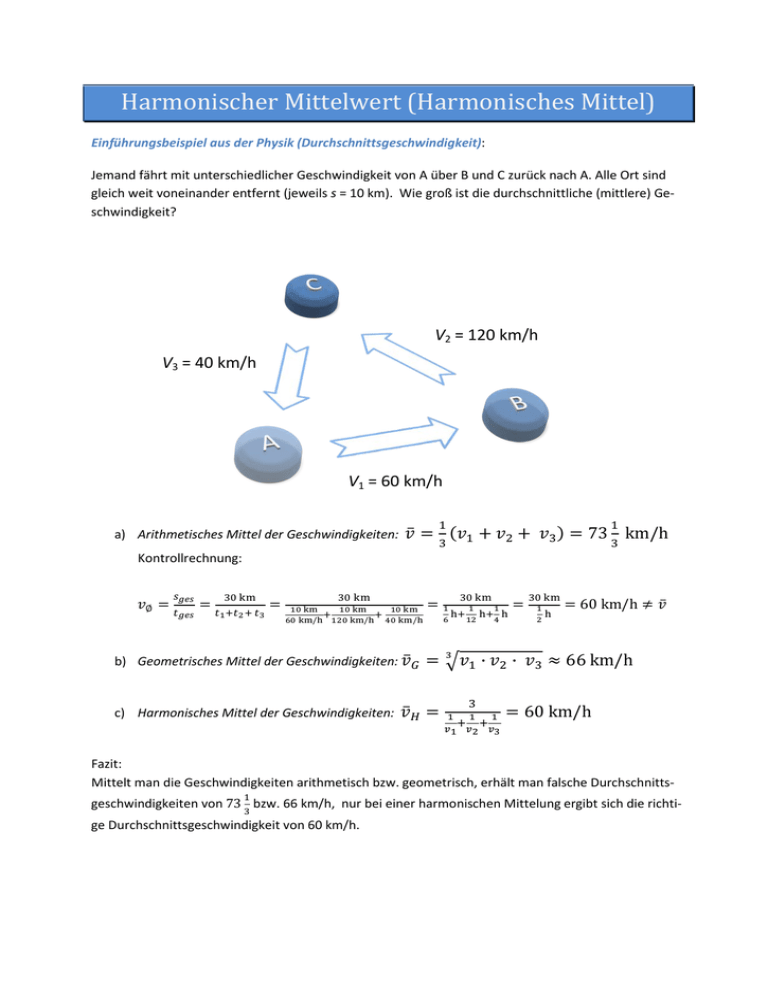
Harmonischer Mittelwert (Harmonisches Mittel)
Einführungsbeispiel aus der Physik (Durchschnittsgeschwindigkeit):
Jemand fährt mit unterschiedlicher Geschwindigkeit von A über B und C zurück nach A. Alle Ort sind
gleich weit voneinander entfernt (jeweils s = 10 km). Wie groß ist die durchschnittliche (mittlere) Geschwindigkeit?
V2 = 120 km/h
V3 = 40 km/h
V1 = 60 km/h
a) Arithmetisches Mittel der Geschwindigkeiten:
Kontrollrechnung:
𝑠𝑔𝑒𝑠
𝑣∅ = 𝑡
𝑔𝑒𝑠
=𝑡
30 km
1 +𝑡2 + 𝑡3
=
1
3
30 km
10 km
10 km
10 km
+
+
60 km/h 120 km/h 40 km/h
b) Geometrisches Mittel der Geschwindigkeiten: 𝑣̅ 𝐺
c) Harmonisches Mittel der Geschwindigkeiten:
1
𝑣̅ = (𝑣1 + 𝑣2 + 𝑣3 ) = 73 km/h
=1
6
3
30 km
h+
1
1
h+ h
12
4
=
30 km
1
h
2
= 60 km/h ≠ 𝑣̅
= 3�𝑣1 ∙ 𝑣2 ∙ 𝑣3 ≈ 66 km/h
𝑣̅𝐻 =
3
1
1
1
+ +
𝑣1 𝑣2 𝑣3
= 60 km/h
Fazit:
Mittelt man die Geschwindigkeiten arithmetisch bzw. geometrisch, erhält man falsche Durchschnitts1
3
geschwindigkeiten von 73 bzw. 66 km/h, nur bei einer harmonischen Mittelung ergibt sich die richtige Durchschnittsgeschwindigkeit von 60 km/h.
Allgemein gilt für den harmonischen Mittelwert von n Werten die Formel: 𝑥̅𝐻
bzw. als Kehrwert geschrieben:
1
𝑥̅ 𝐻
1
1
1
1
= � + +⋯+ �
𝑛 𝑥
𝑥
𝑥
1
2
=
𝑛
1
1
1
+ +⋯+
𝑥1 𝑥2
𝑥𝑛
𝑛
Anwendungsbeispiel aus der Biologie (Mittlerer Überlebenszeit von Versuchstieren):
Bei einem toxikologischen Langzeitversuch wurden 20 Monate nach Versuchsbeginn die Überlebenszeiten von 9 Ratten protokolliert (siehe Tabelle). Berechnen Sie daraus die mittlere Überlebenszeit.
Tier Nr.
Überlebenszeit in d
1
2
3
4
295
318
377
270
5
überlebt
6
109
7
überlebt
8
9
278
114
Lösung:
Die 2 überlebenden Tiere sind irgendwann nach 20 Monaten gestorben. Deren Todeszeitpunkt stand
aber nicht im Zusammenhang mit dem Versuch. Die Überlebenszeiten dieser Tiere werden deshalb
gleich ∞ gesetzt und die zugehörigen Kehrwerte gleich 0 (= 1/∞).
̅ =
𝑡𝐻
𝑛
1 1
1
𝑡1 + 𝑡2 + ⋯ + 𝑡𝑛
=
9𝑑
1
1
1
1
1
1
1
+
+
+
+ 0 + 109 + 0 + 278 + 114
295 318 377 270
≈ 261,4 𝑑
Zusammenhang zwischen arithmetischem, geometrischem und harmonischem Mittel (n=2)
(Höhensatz bzw. Kathetensatz)
𝑥̅𝐺 = √𝑎 ∙ 𝑏
�
𝒙𝑯 =
𝑎
𝟐
𝟏 𝟏
+
𝒂 𝒃
=
𝑥̅𝐻
𝟐𝒂𝒃
<�
𝒙𝑮 < �
𝒙
𝒂+𝒃
𝑥̅ =
𝑎+𝑏
2
𝑏