Document
Werbung
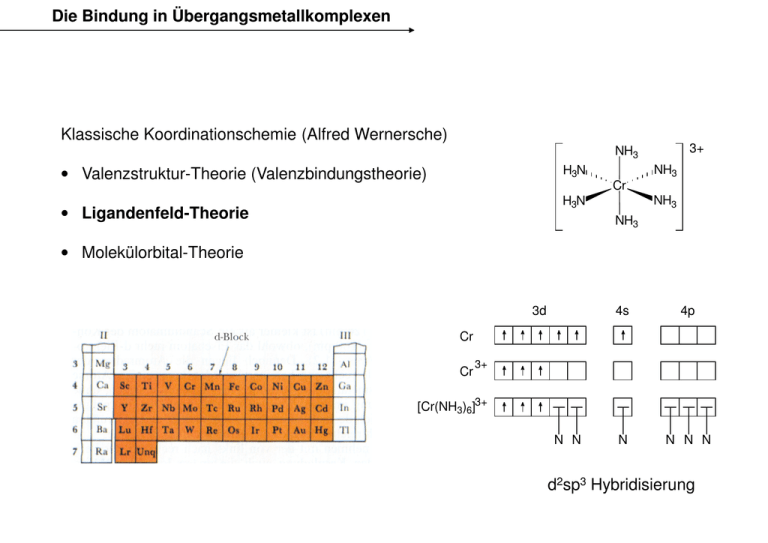
Die Bindung in Übergangsmetallkomplexen Klassische Koordinationschemie (Alfred Wernersche) 3+ NH3 H3N • Valenzstruktur-Theorie Theorie (Valenzbindungstheorie) Cr NH3 H3N • Ligandenfeld-Theorie NH3 NH3 • Molekülorbital-Theorie 3d 4s 4p N N N N Cr Cr 3+ [Cr(NH3)6]3+ N N d2sp3 Hybridisierung Maximierung repulsiver Wechselwirkungen um das Metall Kristallfeld-Theorie Kristallfeld-Theorie Theorie wurde zunächst entwickelt, um die Farbe von Feststoffen zu erklären. O O O Al 3+ O O O O O O C Cr 3+ O O O O 3+ Fe O O O O O Korund (α-Al2O3) Rubin (Al2O3 · x Cr2O3) Topas (Al2O3 · x Fe2O3) Rein elektrostatisches Modell: • Liganden und Zentralatom als sich gegenseitig beeinflussende Punktladungen (keine kovalenten Anteile, keine Orbitalüberlappungen). • Das elektrische Feld der Liganden beeinflusst die Orbitale des Zentralatoms - die Entartung der d-Orbitale Orbitale wird aufgehoben. • Nur Betrachtung der d-Orbitale - restliche Orbitale bilden gefüllte Schalen. Mn+ Oktaederfeld dx2-y2 dxy dz 2 dxz dyz Annäherung der Liganden an das freie Zentralion aus den Richtungen x, -x, y, -y, z, -z: • dx2-y2-, dz2-AO's liegen auf den Achsen → große elektrostatische Abstoßung. • dxy-, dxz-, dyz-AO's AO's liegen zwischen den Achsen → geringe elektrostatische Abstoßung. Orbitalaufspaltung im Oktaederfeld E = hν = h c = hc~ ν λ Die Oktaederfeldaufspaltung ∆O = 10 DqO liegt in der Größenordnung von ∆O = ~ ν = 84 7000 - 480 40000 kJ/mol cm-1 = 1430 - 250 nm λ d1-Elektronenkonfiguration Bei d1-Elektronenkonfigurationen Elektronenkonfigurationen ist die direkte Messung von ∆O= 10 Dq möglich. Absorptionsspektrum von [Ti(H2O)6]3+ Übergang t2g1 eg0 → t2g0 eg1 ~ ν λ ∆O c E = hν = h = hc~ ν λ ≈ ≈ ≈ 20000 cm-1 500 nm 240 kJ/mol [ReF6]: ∆O ≡ 32500 cm-1 Ein etwas genauerer Blick Beispiel: d2 h hv Grundzustand Angeregter Zustand Vorraussage: eine Absorptionsbande Aber Experiment: 2 Banden 10000 Grund: 20000 30000 Wellenzahlen e- e- Vernachlaessigung der elektrostatischen Elektron-Elektron Coulomb Abstossung Elektronenbesetzung der Orbitale beim Oktaeder Ligandenfeldstabilisierungsenergie (LFSE): Energiegewinn gegenüber dem Ion im sphärischen Feld d1 (Ti3+) d2 (V3+) d3 (Cr3+) eg eg eg t2g t2g t2g LFSE = -0,4 ∆O = -4 DqO LFSE = -8 DqO LFSE = -12 DqO 1. Hundsche Regel: Regel der maximalen Multiplizität Elektronenbesetzung der Orbitale beim Oktaeder Spinpaarungsenergie (P): Energie, die aufgebracht werden muss, um zwei Elektronen in einem Orbital unterzubringen (1. Coulombsche Abstoßung; 2. Verlust an Austauschenergie). d5 (Mn2+, Fe3+) d4 (Cr2+) high-spin low-spin eg eg t2g LFSE = -6 DqO ∆O < P high-spin ∆O > P eg eg t2g t2g LFSE = -16 Dq + P low-spin LFSE = 0 ∆O < P t2g LFSE = -20 Dq + 2 P ∆O > P Elektronenbesetzung der Orbitale beim Oktaeder d6 (Fe2+, Co3+) high-spin low-spin t2g LFSE = -4 DqO high-spin eg eg ∆O < P d7 (Co2+) ∆O > P eg eg t2g t2g LFSE = -24 Dq + 2 P low-spin LFSE = -8 DqO ∆O < P t2g LFSE = -18 Dq + P ∆O > P Für d4-, d5-, d6-, d7-Konfigurationen Konfigurationen sind highhigh und low-spin-Anordnungen möglich. Elektronenbesetzung der Orbitale beim Oktaeder d8 (Ni2+) d9 (Cu2+) d10 (Zn2+) eg eg eg t2g t2g t2g LFSE = -12 DqO LFSE = -6 DqO LFSE = 0 DqO Für d1-, d2-, d3- sowie für d8- d9-, d10-Konfigurationen Konfigurationen kann keine Unterscheidung zwischen high- und low-spin spin Anordnung getroffen werden. Für d4-, d5-, d6-, d7-Konfigurationen Konfigurationen sind highhigh und low-spin-Anordnungen möglich. Faktoren, die ∆O beeinflussen 1. Die Oxidationsstufe des Metallions ∆O nimmt mit steigender Oxidationsstufe des Metallions zu. [Ru(H2O)6]2+ [Ru(H2O)6]3+ [CrF6]3- [CrF6]2- ∆O ≡ 19800 cm-1 ∆O ≡ 28600 cm-1 ∆O ≡ 15600 cm-1 ∆O ≡ 22000 cm-1 2. Die Art des Metallions (3d nach unten (5d-Elemente) zu. ∆O nimmt innerhalb einer Gruppe von oben (3d-Elemente) Konsequenz: 4d- und 5d-Elemente Elemente liegen immer (bis auf eine Handvoll Ausnahmen) in der low-spin-Konfiguration vor. [Co(NH3)6]3+ [Rh(NH3)6]3+ [Ir(NH3)6]3+ ∆O ≡ 22870 cm-1 ∆O ≡ 34100 cm-1 ∆O ≡ 41200 cm-1 Irving-Williams Reihe Mn2+ < Ni2+ < Co2+ < Fe2+ < V2+ < Fe3+ < Cr2+ < Co3+ < Ru2+ < Mn4+ < Mo3+ < Rh3+ < Ru3+ < Pd4+ < Ir3+ < Pt4+ Faktoren, die ∆O beeinflussen 3. Die Art der Liganden Spektrochemische Reihe: Messung von ∆O (nicht mit nur einem Metall möglich) I− < Br− < S2−− < SCN− < Cl− < NO3− < F− < OH− < C2O42−− < H2O < NCS− < CH3CN < NH3 < NO2− < PPh3 < CN− < CO FeSO4 · 7 H2O K4[Fe(CN)6] "Gelbes Blutlaugensalz" "Eisenvitriol" H2O Fe OH2 N OH2 H2O O H2 4- N 2+ H2 O N paramagnetisch diamagnetisch C C C C N Fe C C N N Cobaltammine [Co(NH3)5Cl]Cl2 "Purpureosalz" 2+ Cl H3N Co H3N [Co(NH3)5H2O]Cl3 "Roseo Roseosalz" H3N NH3 H3N NH3 λmax = 530 3+ OH2 NH3 Co [Co(NH3)5NH3]Cl3 "Luteosalz" NH3 H3N NH3 H3N NH3 Co NH3 NH3 NH3 λmax = 495 E=h 3+ NH3 λmax = 457 c = hc~ ν λ Gang der Hydratationsenthalpien der M2+-Ionen Ionen [M(OH2)6]2+-Ionen Ionen sind high spin! Werte nach Abzug der jeweiligen LFSE Radien zwei- und dreiwertiger 3d-Ionen offene Kreise: high spin gefüllte Kreise: low spin Beeinflussung der Redoxpotentiale 2+ H2 O H2O Co OH2 OH2 H2O O H2 K3[Co(CN)6] [Co(NH3)6]Cl3 [Co(H2O)6]Cl2 H3N C Co NH3 NH3 H3N N H3 3- N 3+ H3 N N N C C C C N Co C C N N E°(Co2+/Co3+) = E°(Co2+/Co3+) = E°(Co2+/Co3+) = 1,83 V 0,108 V -0,83 V Tetragonale Verzerrung des Oktaeders Sauerstofftransport über Eisen Myoglobin: O2-bindend, im Muskelgewebe 153 Aminosäuren: Globin Prostetische Gruppe: Eisenprotoporphyrin IX CO 2 - Verankerung im Globin über ein Histidin distal N N FeII N CO 2 - N N Fe N N N N HN proximal CO 2 CO 2 - Sauerstofftransport über Eisen Hämoglobin: reversibel O2-bindend, in den Erythrozyten ααββ-Struktur (141 bzw. 146 Aminosäuren) Prostetische Gruppe: Eisenprotoporphyrin IX Sauerstofftransport über Eisen Hämoglobin: UV/vis: 400 – 600 nm (intensiv, Soret-Bande) π→π*-Übergänge des Porphyrins 1105 cm-1 Resonanz-Raman: O-O-Streckschwingung - Superoxid O2 end-on-Bindung Fe(II) → Fe(III) NN NN Fe CO 2CO 2 O2 O NN Fe N HN N HN O NN CO2CO 2 Sauerstofftransport über Eisen NN NN Fe O CO 2CO 2 O2 NN Fe N NN N HN HN paramagnetisch diamagnetisch x2-y2 x2-y 2 2 z2 z O xz,yz xy xy x xz,yz Fe(III) low spin Fe(II) high spin r = 92 pm ∆Ionenradius = 25 % r = 69 pm CO 2CO 2 Tetraederfeld ∆T = 4/9 ∆O Tetraederfeld MO-Diagramm Oktaeder