19 Idealer Wirkwiderstand im Wechselstromkreis

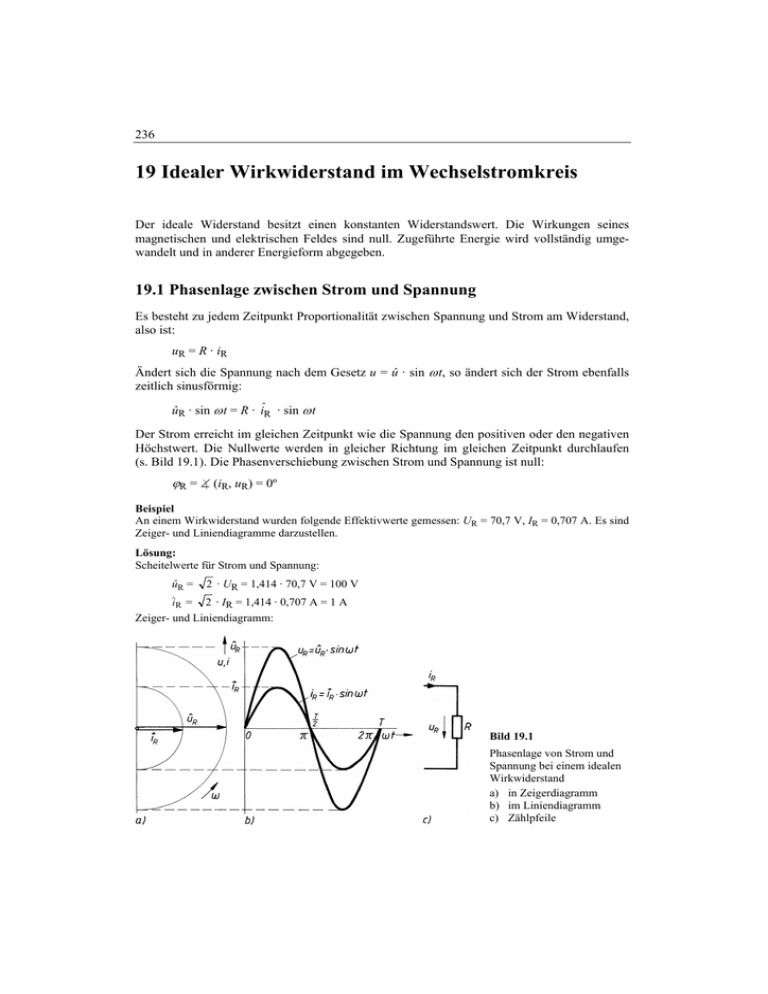
236
19 Idealer Wirkwiderstand im Wechselstromkreis
Der ideale Widerstand besitzt einen konstanten Widerstandswert. Die Wirkungen seines
magnetischen und elektrischen Feldes sind null. Zugeführte Energie wird vollständig umgewandelt und in anderer Energieform abgegeben.
19.1 Phasenlage zwischen Strom und Spannung
Es besteht zu jedem Zeitpunkt Proportionalität zwischen Spannung und Strom am Widerstand,
also ist:
uR = R · iR
Ändert sich die Spannung nach dem Gesetz u = û · sin ω t, so ändert sich der Strom ebenfalls
zeitlich sinusförmig:
ûR · sin ω t = R · îR · sin ω t
Der Strom erreicht im gleichen Zeitpunkt wie die Spannung den positiven oder den negativen
Höchstwert. Die Nullwerte werden in gleicher Richtung im gleichen Zeitpunkt durchlaufen
(s. Bild 19.1). Die Phasenverschiebung zwischen Strom und Spannung ist null:
ϕR = ∠
⎞ (iR, uR) = 0º
Beispiel
An einem Wirkwiderstand wurden folgende Effektivwerte gemessen: UR = 70,7 V, IR = 0,707 A. Es sind
Zeiger- und Liniendiagramme darzustellen.
Lösung:
Scheitelwerte für Strom und Spannung:
ûR =
2 · UR = 1,414 · 70,7 V = 100 V
R = 2 · IR = 1,414 · 0,707 A = 1 A
Zeiger- und Liniendiagramm:
^i
Bild 19.1
Phasenlage von Strom und
Spannung bei einem idealen
Wirkwiderstand
a) in Zeigerdiagramm
b) im Liniendiagramm
c) Zählpfeile
19.2 Leistungen und Energieumsetzung
237
19.2 Leistungen und Energieumsetzung
Betrachtet man die Energieumsetzung eines Verbrauchers (z.B. eines Heizwiderstandes) in
Bild 19.2 innerhalb einer Folge kleinster Zeitabschnitte dt, so erkennt man, dass die je Zeitabschnitt umgewandelte Energiemenge schwankend ist. Die direkte Beobachtung des Heizwiderstandes zeigt dagegen bei ausreichend hoher Frequenz der Wechselspannung eine gleichmäßige Energieabgabe des Verbrauchers. Die Temperatur des Heizwiderstandes richtet sich offensichtlich nach einem Durchschnittswert der Momentanleistungen, der nachfolgend ermittelt
werden soll:
In einem beliebigen Zeitpunkt t besteht eine Momentanspannung uR und ein Momentanstrom
iR am Widerstand. Die in diesem Augenblick bestehende Geschwindigkeit der Energiezuführung – also die Leistung – beträgt:
p(t) = uR · iR
oder
p(t) = ûR · sin ω t · ^i R · sin ω t
p(t) = ûR · ^i R · sin2 ω t
Mit der trigonometrischen Umformung:
sin 2 ω t =
1
(1 − cos 2ω t )
2
wird:
uˆ ⋅iˆ
uˆ ⋅iˆ
p(t ) = R R − R R cos 2 ωt
2
2
Mit den Effektivwerten von Strom und Spannung ergibt sich der zeitliche Verlauf der Leistung zu:
p(t) = UR · IR – UR · IR · cos 2 ω t
Bild 19.2 zeigt anschaulich den zeitlichen Verlauf dieser Funktion. Bei dem Momentanwert
null von Strom und Spannung ist auch die Leistung momentan null. Bei den Maximalwerten
von Strom und Spannung ist die Leistung maximal.
Der Durchschnittswert P aus dem zeitlichen Verlauf der Momentanleistung p(t) über eine volle
Periode des Wechselstromes wird Wirkleistung P genannt:
P=
1T
∫ p(t )⋅dt
T 0
(127)
Speziell für den sinusförmigen Strom im Wirkwiderstand ist die Wirkleistung gleich dem
Durchschnittswert aus dem zeitlichen Verlauf der Momentanleistung. Wie Bild 19.2 zeigt, ist
dieser Durchschnittswert
P = U R ⋅ I R , wenn ϕR = 0º.
Einheit 1 W
(128)
238
19 Idealer Wirkwiderstand im Wechselstromkreis
In Worten: Die Wirkleistung P des idealen Wirkwiderstandes errechnet sich bei sinusförmigen
Wechselstrom aus dem Produkt der Effektivwerte von Wechselspannung und Wechselstrom.
Die Wirkleistung ist die durchschnittliche Arbeitsgeschwindigkeit, mit der elektrische Energie
in andere Energie umgewandelt und an die Umgebung abgegeben wird.
Beispiel
An einem Widerstand wurden gemessen: UR = 70,7 V, IR = 0,707 A.
Es ist die Funktion p(t) = f (ω t) zu ermitteln und daraus die Wirkleistung zu bestimmen.
Lösung: Der zeitliche Verlauf der Leistung wird in einer Tabelle berechnet:
ωt
0
30º
45º
60º
90º
120º
135º
150º
180º
360º
cos 2 ω t
p(t) = UR · IR – UR · IR · cos 2 ω t
+1
0W
+ 0,5
+
25 W
0
+
50 W
– 0,5
+
75 W
–1
+ 100 W
– 0,5
+
75 W
0
+
50 W
+ 0,5
+
25 W
+1
0W
Wiederholung der Werte
+1
0W
∅ = 50 W
Bild 19.2 zeigt den zeitlichen Verlauf der Leistung. Man erkennt eine Leistungsschwingung mit doppelter Frequenz gegenüber der Frequenz des Wechselstromes. Der Durchschnittswert aller Momentanleistungen über eine volle Periode beträgt:
T
P=
1
∫ p(t )⋅dt = 50 W
T 0
Die Wirkleistung kann auch einfach aus
P = UR · IR = 70,7 V · 0,707 A = 50 W errechnet werden.
Bild 19.2
Die Leistung p(t) der dem Wirkwiderstand zugeführten Energie
schwingt mit doppelter Frequenz um
den Mittelwert P = UR · IR
19.3 Ohm’sches Gesetz, Wirkwiderstand
239
Im Liniendiagramm der Momentanleistung wurde ein Flächenstreifen unter der Funktionskurve eingetragen (s. Bild 19.2). Es besitzt eine Grundlinie d(ω t), die bei einer bestimmten Frequenz; der Zeit dt entspricht. Die Höhe des Flächenstreifens ist mit genügender Genauigkeit
p(t). Die Fläche „p(t) · dt“ entspricht einer während der Zeit dt dem Widerstand zugeführten
elektrischen Energie dW. Die Summe aller Flächenstreifen von 0 bis T ist folglich gleich der
während der Zeit einer Periode aufgewendeten elektrischen Energie:
W=
1T
∫ p(t )⋅dt
T 0
Mit dem Mittelwert der Leistung P = UR ⋅ IR und der Zeitdauer t des Bestehens dieser Leistung
über volle Perioden ist die im Wirkwiderstand in Wärme umgesetzte elektrische Energie:
WR = U R ⋅ I R ⋅t
Einheit 1 Ws
(129)
Diese elektrische Arbeit, die durch registrierende Messgeräte (Zähler) gemessen werden
kann, wird Wirkarbeit genannt. Kennzeichen der Wirkarbeit ist die vollständige Umwandlung
und Abgabe der zugeführten elektrischen Energie. Die in Bild 19.2 gerasterte Fläche stellt die
Wirkarbeit dar, die in einer Periodendauer T verrichtet wird.
Wirkarbeit bedeutet jedoch nicht immer Wärmeerzeugung. Ein Motor verrichtet z.B. Wirkarbeit durch Abgabe von mechanischer Energie.
19.3 Ohm’sches Gesetz, Wirkwiderstand
Ein sinusförmiger Strom verursacht an einem idealen Wirkwiderstand einen sinusförmigen
Spannungsabfall:
uR ⋅sin ω t = R⋅i⋅sin ω t
Deshalb ist auch
ûR = R⋅iˆR
und mit den Effektivwerten:
U R = R⋅ I R
(130)
Diese Beziehung ist das Ohm’sche Gesetz für den Widerstand bei Wechselspannung. Der
darin enthaltene Widerstand R wird Wirkwiderstand genannt. Mit dem Begriff Wirkwiderstand
ist verbunden, dass bei Anlegen einer Wechselspannung ein phasengleicher Wechselstrom
auftritt und die gesamte ihm zugeführte elektrische Energie vollständig umgewandelt und in
andere Energieform abgegeben wird. Allgemein gültig ist deshalb die Bestimmung des Wirkwiderstandes über die Wirkleistung:
R=
P
I R2
oder
R=
U R2
P
(131a, b)
240
19 Idealer Wirkwiderstand im Wechselstromkreis
Beispiel
Bei einem Wirkwiderstand an sinusförmiger Wechselspannung werden die Effektivwerte UR = 70,7 V
und IR = 0,707 A gemessen. Ein Leistungsmesser zeigt die Leistungsaufnahme P = 50 W des Wirkwiderstandes an. Wie groß ist der Wirkwiderstand R?
Lösung:
Mit den Effektivwerten von Strom und Spannung:
R=
UR
70,7 V
=
= 100 Ω
IR
0,707 A
Über die Wirkleistung:
R=
P
I R2
=
50 W
(0,707 A) 2
2
= 100 Ω
oder
R=
U R2 ( 70,7 V )
=
= 100 Ω
P
50 W
Der Begriff des Wirkwiderstandes ist jedoch nicht so einfach, wie er im voranstehenden Beispiel erscheint. Dort ist der Wirkwiderstand gleich dem Leitungswiderstand des verwendeten
Drahtwiderstandes. Bei Betrieb an Gleichspannung U = 70,7 V würde sich der Gleichstrom
I = 0,707 A einstellen, da der Widerstand bei Gleichstrom und auch bei niederfrequentem
Wechselstrom durch die Drahtlänge, den Drahtquerschnitt und den spezifischen Widerstand
bestimmt wird.
Wirkwiderstand = Leitungswiderstand, gilt bei Gleichstrom und Wechselstrom sehr
niedriger Frequenz
Bei erhöhten Frequenzen stellt man fest, dass der Wirkwiderstand sich gegenüber dem Leistungswiderstand offensichtlich vergrößert hat. Man führt dies auf den Effekt der Stromverdrängung zurück: Der Strom fließt nicht mehr im vollen Leiterquerschnitt, sondern nur noch
an der Oberfläche des Leiters, wodurch sich die wirksame Drahtquerschnittfläche verringert
hat.
Wirkwiderstand > Leitungswiderstand, gilt bei erhöhten Frequenzen
In einigen Fällen ist der Wirkwiderstand nicht die Eigenschaft eines Drahtwiderstandes, an
dem Messungen durchgeführt werden können, sondern ein Ersatzwiderstand für die Verluste
des magnetischen und elektrischen Feldes. So kann z.B. die Eisenerwärmung eines Transformators infolge ständiger Ummagnetisierung durch einen Ersatzwiderstand schaltungsgemäß
erfasst werden. Neben diesen sog. Ummagnetisierungsverlusten im magnetischen Feld gibt es
bei Kondensatoren und Leitungen sog. dielektrische Verluste. Diese zeigen sich als eine Erwärmung des Dielektrikums infolge ständiger Umpolung der Dipolmoleküle und können ebenfalls durch einen Ersatzwiderstand schaltungsgemäß erfasst werden. Diese Ersatzwiderstände
für die Verluste des magnetischen und elektrischen Feldes sind Wirkwiderstände, die überhaupt nichts mit dem Gleichstromwiderstand von Drähten zu tun haben.
Wirkwiderstand als Ersatzwiderstand für die Verluste des magnetischen und elektrischen Feldes
19.4 Übungsaufgaben
241
Ferner wird der Begriff des Wirkwiderstandes auch so verwendet, dass eine beabsichtigte,
nützliche Energieumwandlung durch einen Wirkwiderstand schaltungsmäßig dargestellt wird
wie z.B. die Energieumwandlung in einer Antenne, bei der elektrische in elektromagnetische
Leistung ungesetzt wird.
Wirkwiderstand als Ersatzwiderstand für eine beabsichtigte, nützliche Leistungsumwandlung
Deshalb gilt: Der Wirkwiderstand R ist der aus der Wirkleistung P und dem Effektivwert I des
Stromes bestimmte Wechselstrom-Widerstandswert eines Bauelementes.
19.4 Übungsaufgaben
Δ Übung 19.1: Leistungsschwingung
In einem Wirkwiderstand R = 100 Ω fließt ein sinusförmiger Wechselstrom mit der Amplitude 50 mA
und Frequenz 500 Hz.
a) Wie groß ist die Wirkleistung?
b) Wie groß sind Maximal- und Minimalwerte der Momentanleistung?
c) Wie groß ist die Frequenz der Leistungsschwingung?
• Übung 19.2: Widerstandsbegriffe
Grenzen Sie die Begriffe
– ohmscher Widerstand,
– Gleichstromwiderstand,
– Wirkwiderstand
gegeneinander ab.
Δ Übung 19.3: Wirkleistung
Welche Leistung müsste ein Leistungsmesser in einer Schaltung anzeigen, bei der ein Wirkwiderstand
von 23 Ω an Netzwechselspannung u = 325 V · sin ω t liegt?
Δ Übung 19.4: Wirkwiderstand und Wirkleistung
Welchen Wirkwiderstand hat ein Heizleiter, der an Netzspannung 230 V ( f = 50 Hz) innerhalb von
t = 1 min die elektrische Energie 10 Wh verbraucht, d.h. in Wärme umwandelt ?
Δ Übung 19.5: Effektivwert
Wie groß ist der Wirkwiderstand des Verbrauchers, wenn ein sinusförmiger Strom der Amplitude 0,4 A
die Leistungsmesseranzeige 50 W verursacht?
Δ Übung 19.6: Ersatz-Wirkwiderstand
Eine 65 W-Leuchtstofflampe wird mit einem
sog. Vorschaltgerät an 230 V Netzwechselspannung betrieben.
Die Aufgaben des Vorschaltgerätes sind das
Zünden der Leuchtstofflampe und die Aufnahme des Spannungsüberschusses während
des Betriebes. Nach erfolgter Zündung wird
eine Stromaufnahme von 0,68 A gemessen.
Wie groß ist der Ersatz-Wirkwiderstand R der
gezündeten Leuchtstofflampe?
Bild 19.3