Präsentation zu Wechselstrom-Grundschaltungen
Werbung

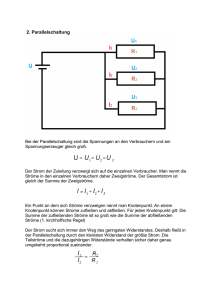
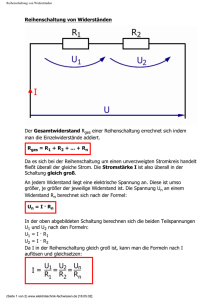
20.03.2009 Grundschaltungen im Wechselstromkreis 1. 2. 3. 4. Reihenschaltung von Wirkwiderstand und idealer Induktivität Reihenschaltung von Wirkwiderstand und idealer Kapazität Parallelschaltung von Wirkwiderstand und idealer Induktivität Parallelschaltung von Wirkwiderstand und idealer Kapazität 5. 6. RCL-Reihenschaltungen RCL-Parallelschaltungen 7. 8. Realer Kondensator Reale Spule 1.Reihenschaltung aus Wirkwiderstand R und induktivem Blindwiderstand XL: Auswertung: der Strom i (I) ist in Phase mit der Spannung uw (Uw) → der Phasenwinkel zwischen der Spannung am Wirkwidersand und dem Strom ist Null ---> φ = 0° der Phasenwinkel zwischen der Gesamtspannung ug (Ug) und dem Strom i (I) ist kleiner 90° ---> φ < 90° ug eilt i voraus der Phasenwinkel zwischen der Spannung uL (UL) und dem Strom i (I) ist 90° ---> φ = 90° eilt i um 90°voraus uL 1 20.03.2009 Zeigerdiagramme und -bilder: Berechnungen : Ug = Uw +UL 2 2 cos ϕ = Uw Ug 2 Ug = Uw +UL → sin ϕ = 2 UL Ug 2 → tan ϕ = UL Uw Auswertung: zeigt die Abhängigkeit des Phasenwinkels φ von der Gesamtspannung Ug und des Stromes I → φ ist abhängig von Verhältnis des Wirkwiderstandes R zum Blindwiderstand XL → R > XL (Uw > UL) → φ ↓ → 0°→ es wirkt nur noch der reine Wirkwiderstand R → R < XL (Uw < UL) → φ ↑ → 90° → es wirkt nur noch der reine Blindwiderstand XL Scheinwiderstand Z (Impedanz) Berechnung en : Scheinwide rs tand : Z= Ug I U Wirkwiders ta n d : R= w I UL Blindwider sta n d : X L = I R XL X cos ϕ = sin ϕ = tan ϕ = L Z Z R 2 20.03.2009 Scheinleistung S → S = U ⋅ I [VA] Auswertung: in der Reihenschaltung von R und XL entsteht sowohl Wirk- [P] als auch Blindleistung [QL] das Produkt aus U und I (Effektivwerte] ist die Scheinleistung [S], in der P und QL enthalten sind Praktische Bedeutung erhält die Scheinleistung im Zusammenhang mit der Auslegung von Leiterquerschnitten bei Transformatoren und Generatoren in der Energietechnik die Augenblickswerte verlaufen sowohl oberhalb (u und i haben gleiche Richtung) als auch unterhalb der Zeitachse (u und i haben entgegengesetzte Richtung) es werden Wirk- und Blindarbeit verrichtet Berechnung en : Wirkleistu ng : P = U W ⋅ I [W ] Blindleist ung : QL = U L ⋅ I [var ] Scheinleis tung : S = U g ⋅ I [VA ] S 2 = P 2 + QL cos ϕ = S =Ug ⋅I P S 2 S= P 2 + QL QL S P = U g ⋅ I ⋅ cos ϕ sin ϕ = 2 QL P Q L = U g ⋅ I ⋅ sin ϕ tan ϕ = 3 20.03.2009 Messtechnische Ermittlungen von S und P: Scheinleistung S Wirkleistung P Leistungsfaktor : cos ϕ = P S gibt an wie viel Leistung von S in P umgesetzt wird steht z.B. auf Typenschilder von Drehstrommotoren cos φ = 1 → P = S → QL = 0 → Kompensation günstigster Fall! Energietechnik: kleiner cos φ → I ↑ → gewählter Leiterquerschnitt ↑ → höhere Kosten Reihenschaltung aus Wirkwiderstand R und kapazitivem Blindwiderstand XC Auswertung: i ist mit uw in Phase → φ = 0° i eilt ug voraus → φ < 90° i eilt uc voraus → φ = 90° 4 20.03.2009 Reihenschaltung aus Wirkwiderstand R und kapazitivem Blindwiderstand XC Parallelschaltung aus Wirkwiderstand R und kapazitivem Blindwiderstand XC Auswertung: iw ist mit ug in Phase → φ = 0° ig eilt ug voraus → φ < 90° ic eilt ug voraus → φ = 90° 5 20.03.2009 Parallelschaltung aus Wirkwiderstand R und kapazitivem Blindwiderstand XC Berechnungen : I g = I w + IC → I g = I w + IC 2 cosϕ = 2 Iw Ig 2 sin ϕ = 2 IC Ig 2 tan ϕ = IC IW Auswertung: zeigt die Abhängigkeit des Phasenwinkels φ von dem Gesamtstrom Ig und der Spannung U → φ ist abhängig von Verhältnis des Wirkwiderderstandes R zum Blindwiderstand XC → XC > R (Ic < Iw) → φ ↓ → 0°→ es wirkt nur noch der reine Wirkwiderstand R Parallelschaltung aus Wirkwiderstand R und kapazitivem Blindwiderstand XC → XC < R (IC > Iw) → φ ↑ → 90° → es wirkt nur noch der reine Blindwiderstand XC 6 20.03.2009 Parallelschaltung aus Wirkwiderstand R und kapazitivem Blindwiderstand XC Parallelschaltung aus Wirkwiderstand R und kapazitivem Blindwiderstand XC 1 R Wirkleitwert G= Blindleitwert BC = Scheinleitwert Y = Y= 1 XC 1 (Admittanz) Z Ig U Y2 = G2 + BC2 → Y = G2 + BC2 7 20.03.2009 Parallelschaltung aus Wirkwiderstand R und kapazitivem Blindwiderstand XC Parallelschaltung aus Wirkwiderstand R und induktivem Blindwiderstand XL Auswertung: iw ist mit ug in Phase → φ = 0° ig eilt ug nach → φ < - 90° iL eilt ug nach →φ = - 90° 8 20.03.2009 Parallelschaltung aus Wirkwiderstand R und induktivem Blindwiderstand XL Reihenschaltung aus Wirkwiderstand R, induktivem Blindwiderstand XL und kapazitivem Blindwiderstand XC (RLC-Reihenschaltung): Auswertung: UL und UC sind phasenverschoben φ = 180° UL > UC → XL > XC (Reihenschaltung!) Gesamte Schaltung hat ein induktives Verhalten 9 20.03.2009 Reihenschaltung aus R, XL und XC, RLC-Reihenschaltung Gesamte Schaltung hat ein induktives Verhalten Reihenschaltung aus R, XL und XC, Zeigerdiagramm und Zeigerbilder Auswertung: UL < UC → XL < XC Z = Gesamte Schaltung hat ein kapazitives Verhalten R 2 + (X C - X L ) 2 Induktive und kapazitive Blindwiderstände haben entgegengesetzte Wirkungen hinsichtlich der Phasenverschiebung ϕ zwischen der Gesamtspannung Ug und dem Strom I. 10 20.03.2009 Reihenresonanz (Spannungsresonanz) Auswertung: UL = UC → XL = XC Zustand der Resonanz Reihenresonanz (Spannungsresonanz) Auswertung: Imax Bei der Resonanzfrequenz fres (fO) ist der Scheinwiderstand Z gleich dem ohmschen Widerstand R und nimmt dabei den kleinsten Wert an, derStrom I nimmt sein Maximum an. Bei einer RLC - Reihenschaltung können im Resonanzfall die Blindspannungen UC und ULsehr hohe (extreme) Werte annehmen. Die Blindspannungen können die Gesamtspannung dabei um ein Vielfaches übersteigen (Spannungsüberhöhung!!!). R Resonanzkurven von Z, I, UC, UL einer RLC-Schaltung Thomsonsche Schwingungsformel 11 20.03.2009 Reihenresonanz (Spannungsresonanz) Thomsonsche Schwingungsformel UL = UC → XL = XC (Zustand der Resonanz) XL = X C 2 Π fres L = fres = 1 2 Π fres C 1 2 Π L C Resonanzkurven von Z, I, UC, UL einer RLC-Schaltung RLC-Parallelschaltung, Schaltung und Zeigerdiagramm Auswertung: IC und IL sind phasenverschoben φ = 180° Schaltung hat ein kapazitives Verhalten IC > IL → XC < XL (Parallelschaltung!) 12 20.03.2009 RLC-Parallelschaltung, Zeigerbilder Schaltung hat ein kapazitives Verhalten Parallelschaltung aus R, XL und XC, Zeigerdiagramm und Zeigerbilder Auswertung: IC und IL sind phasenverschoben φ = 180° IL > IC → XC > XL Schaltung hat ein induktives Verhalten Y = G2 + ( BL - BC ) 2 13 20.03.2009 Parallelresonanz (Stromresonanz) Auswertung: IC = IL → XC = XL Zustand der Resonanz Parallelresonanz (Stromresonanz) Auswertung: bei fres (f0) ist Z = R (Resonanzwiderstand) am Größsten, daher ist der Strom I am kleinsten! → Stromminimum 14 20.03.2009 Realer (technischer) Kondensator verrichtet nicht nur Blindarbeit sondern auch Wirkarbeit geringere elektrische Leitfähigkeit des Dielektrikums Umpolarisierung der Moleküldipole des Dielektrikums Widerstand der Zuleitung und der Kondensatorplatten ⇒ ist nicht verlustfrei ⇒ endlicher Isolationswiderstand ⇒ dielektrische Verluste Ersatzschaltbild δ = 90° - φ → φ = 90° - δ δ = Verlustwinkel, tan δ = d (der Tangens des Verlustwinkels wird als Verlustfaktor d bezeichnet) 15 20.03.2009 Realer (technischer) Kondensator δ = Verlustwinkel, tan δ = d (der Tangens des Verlustwinkels wird als Verlustfaktor d bezeichnet) Verlustfaktor d : d = tan δ = Gp BC = XC 1 = Rp QC Gütefaktor Q : 1 Rp Q = = = Rp ω C d XC Der Gütefaktor ist um so größer, je kleiner die Verluste des Kondensators sind. Die Verluste können meist vernachlässigt werden ⇒ C wird als reiner XC aufgefasst. Reale (technische) Spule Kupferverluste Eisenverluste ⇒ Stromerwärmung der Wicklung und Stromverdrängungsverluste ⇒ Wirbelstrom- und Hystereseverluste (Ummagnetisierungsverluste) δ = 90° - φ → φ = 90° - δ δ = Verlustwinkel, tan δ = d (der Tangens des Verlustwinkels wird als Verlustfaktor d bezeichnet) 16 20.03.2009 Reale (technische) Spule δ = 90° - φ Verlustfaktor d : RV RV 1 d = tan δ = = = XL ω L QL → φ = 90° - δ Gütefaktor Q : 1 XL ω L Q = = = d RV RV Vollständiges Ersatzschaltbild einer verlustbehafteten Spule ESB.: 17