Physik, Wirtschaftsphysik und Lehramt Physik

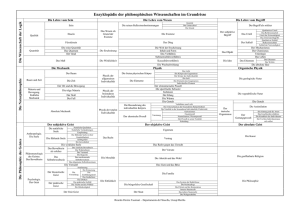
Elektrizitätslehre und Magnetismus
Othmar Marti | 30. 06. 2008 | Institut für Experimentelle Physik
Physik, Wirtschaftsphysik und
Lehramt Physik
Seite 2
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Klausur und Nachklausur
Die Klausur findet am 23. 7. 2008 um 9:00 in H2 und H13 statt
Die Nachklausur findet am 6. 10. 2008 voraussichtlich um 9:00
in H2 statt.
Hilfsmittel: 4 Blätter (8 Seiten) Format A4, von eigener Hand
beschrieben.
Seite 3
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Magnetismus in Materie
Diamagnetische (Bi), paramagnetische (Al) und ferromagnetische
(Fe) Materialien im inhomogenen Magnetfeld.
Seite 4
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Dia-, Para- und Ferromagnetismus
Materie im inhomogenen Magnetfeld zeigt drei verschiedene
Verhalten:
diamagnetisches Verhalten Die Materie wird aus dem starken
magnetischen Feld herausgedrückt.
paramagnetisches Verhalten Die Materie wird in das starke
Feld hineingezogen.
ferromagnetisches Verhalten Die Materie wird in das starke
Feld hineingezogen, aber sehr viel stärker als bei
paramagnetischen Substanzen. Zudem zeigen
diese Substanzen ein remanentes Magnetfeld,
auch wenn das äussere Magnetfeld wieder
verschwunden ist.
Seite 5
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Magnetismus
Wenn der Kreisstrom (die Materie) sich auf der
Symmetrieachse eines rotationssymmetrischen inhomogenen
Magnetfeldes befindet, ist
Fz = mz ·
∂Bz (z, 0)
∂z
wobei mz das induzierte magnetische Moment des
Kreisstromes ist.
Seite 6
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Satz von Larmor
Larmorwinkelgeschwindigkeit
Ω=
e
B
2me
In einem mit der Winkelgeschwindigkeit Ω rotierenden
System sind die Elektronenbahnen im Atom unverändert.
Seite 7
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Larmorfrequenz und Kreisel
Berechnung der Larmorfrequenz mit einem Kreisel
Seite 8
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Satz von Larmor
Man kann den Satz von Larmor aus der Kreiseltheorie ableiten. Das Elektron ist, bei
einer Bahn mit konstantem Radius, ein starrer Körper. Dieser Kreisel hat den
Drehimpuls
L = m · (r × v)
Das magnetische Moment des Kreisstromes ist nach Gleichung (??)
m=−
e
L
2m
Der Kreisel erfährt ein mechanisches Drehmoment
T =m×B
Der Drehimpulssatz bedeutet, dass
dL
e
e
=T =−
L×B =
B×L
dt
2m
2m
Wir erhalten also eine Präzessionsbewegung des Drehimpuslvektors L um B mit der
Winkelgeschwindigkeit Ω
dL
=Ω×L
dt
Seite 9
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Diamagnetismus
Berechnung des Diamagnetismus
mA =
X
j
mj = 0
Seite 10
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Diamagnetismus
Ein einzelner Kreisstrom
Seite 11
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Diamagnetismus
ZR Zπ
ρel = −
Ω=
|mA |
Ze
0
(4/3)πR 3
e
2m
δmA (r , ϕ) drdϕ
=
0
ZR
=
B
π · ρel · Ω ·
Zπ
4
r · dr ·
0
δI = ρel · r · dr · dϕ · v (r , ϕ)
ZR
=
v (r , ϕ) = Ω · r · sin ϕ
π · ρel · Ω ·
4
r · dr ·
0
2
2
δmA (r , ϕ) = Fläche · Strom = πr sin ϕ · δI
=
δmA (r , ϕ)
=
2
2
2
2
4
3
πr sin ϕ · ρel · r · dr · dϕ · v (r , ϕ)
=
πr sin ϕ · ρel · r · dr · dϕ · Ω · r · sin ϕ
=
πr sin ϕ · ρel · Ω · dr · dϕ
π · ρel · Ω ·
=
π·
=
π·
=
Z ·e
4π R 3
3
Z ·e
4π R 3
3
R5
5
·Ω·
·
eB
4
3
4
3
R5
2me
Z · e2 · B · R 2
10me
·
5
·
·
4
3
R5
5
3
sin ϕ · dϕ
0
·
4
3
Seite 12
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Diamagnetismus
mA = −
Z · e2 · R 2
B
10me
Diese diamagnetische Moment ist in allen Atomen
vorhanden. Bei paramagnetischen und ferromagnetischen
Substanzen wird es unterdrückt.
Seite 13
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Atomare Kreisströme
Atomare Kreisströme
j = ma · n = M
Seite 14
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Elektronenspin
sz =
1 h
2 2π
=
1
2
~
Plancksches Wirkungsquantum
−34
Js
−34
Js
h = 6.63 × 10
~=
h
2π
≈ 10
ms = −
e
m
s
e s.
klassische Mechanik: ms = −(1/2) m
e
−23
2
ms,z =
~ ≡ 1µB = 0.927 × 10
A·m
2m
Bohrsches Magneton.
ms = −gµB s
Elektronenspin
Hier ist g der Landé-Faktor , der für die klassische Quantenmechanik g
=
2 ist und
für die Quanten-Elektrodynamik (QED) abhängig von der Atomsorte. Für Wasserstoff (H)
ist gWasserstoff
= 2.002284, für 133 Cs ist
g133 Cs = 2.002540.
Seite 15
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Paramagnetismus
Bei paramagnetischen Atomen hebt sich das magnetische
Bahnmoment der einzelnen Elektronen eines Atoms sowie
deren von den Spins herrührendes magnetisches Moment nicht
vollständig auf.
mA 6= 0
Das magnetische Moment eines paramagnetischen Atoms hat
die Grössenordnung eines Bohrsche Magneton 1µB . Ohne
äusseres Magnetfeld verschwindet die makroskopische
Magnetisierung, da die einzelnen atomaren magnetischen
Momente ungeordnet sind. Im äusseren Magnetfeld ordnen
sich die magnetischen Momente teilweise, da die thermische
Brownsche Bewegung, temperaturabhängig, für Unordnung
sorgt.
Seite 16
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Curie-Gesetz
Schematischer Verlauf der Magnetisierung (Curie-Gesetz für kleine B). MS ist die Sättigungsmagnetisierung.
1 NmA2
C
M=
3 kb T
Hier ist C die Curie-Konstante
C=
B=
mA2
3kb
T
B
Seite 17
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Messung der Magnetisierung
Messung der Hysterese eines Ferromagneten. Rot ist der
Primärkreis, grün der Sekundärkreis.
Seite 18
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Messung der Magnetisierung
Unter Vernachlässigung der Selbstinduktion ist die Differentialgleichung für den
Sekundärkreis
dB(t)
Q(t)
−A ·
−
= R2 · I2 (t)
dt
C
Dabei ist Q(t) die Ladung am Kondensator. Wir schreiben den Strom als zeitliche
Ableitung der Ladung.
A dB(t)
Q(t)
dQ(t)
−
·
=
+
R2
dt
R2 C
dt
Die Anregung in dieser Schaltung ist ein Strom I1 (t), der die Frequenz ω hat. Also ist
auch Q(t) eine periodische Funktion mit der gleichen Frequenz. Bei harmonischen
Funktionen gilt, dass dQ(t)/dt ≈ ωQ(t) ist. Wenn 1/RC ω ist, kann der erste Term
auf der rechten Seite vernachlässigt werden. Dann gilt
Q(t) = const · B(t)
und damit für die Spannung am Kondensator
UC (t) = Q(t)/C ∝ B(t)
Der Ausgangsstrom I(t) selber erzeugt das anregende Feld.
Seite 19
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Hysteresekurve eines Ferromagneten
Hysteresekurve eines Ferromagneten
Seite 20
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Ferromagnetische Domänen
r
Bext = 0
r
Bext
r
Bext
r
M
Änderung der Domänenstruktur bei stärker werdendem äusserem Magnetfeld
Ferromagnetische Domänen ändern die Richtung ihrer
Magnetisierung nicht, sie ändern nur ihre Grösse.
Seite 21
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Löschen des remanenten Magnetismus
Löschen des remanenten Magnetismus
Seite 22
Physik |
Klassische und Relativistische Mechanik |
30. 06. 2008
Gesetze des Elektromagnetismus
Gausssches Gesetz
divE = ρel0
Induktionsgesetz
rotE = − ∂B
∂t
Quellenfreiheit
divB = 0
Durchflutungsgesetz
rotB = µ0 i
Zusätzlich zu den obigen Gleichungen muss die
Kontinuitätsgleichung für Ladungen gelten
divi = −
∂ρel
∂t