Lösungen Ferienaufgaben Mathematik 8 - Gym

Dietrich-Bonhoeffer-Gymnasium Oberasbach
Lösungen Ferienaufgaben Mathematik 8
8.A Funktionen
8.A.1 Begriff
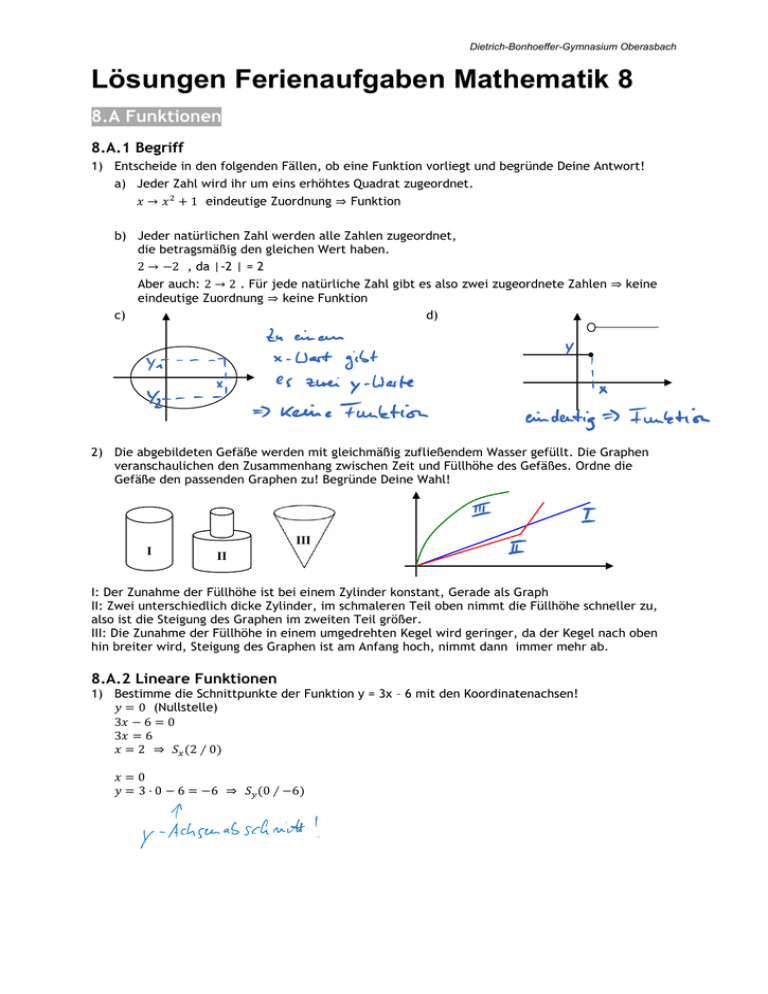
1) Entscheide in den folgenden Fällen, ob eine Funktion vorliegt und begründe Deine Antwort!
a) Jeder Zahl wird ihr um eins erhöhtes Quadrat zugeordnet.
𝑥 → 𝑥 2 + 1 eindeutige Zuordnung ⇒ Funktion
b) Jeder natürlichen Zahl werden alle Zahlen zugeordnet,
die betragsmäßig den gleichen Wert haben.
2 → −2 , da |-2 | = 2
Aber auch: 2 → 2 . Für jede natürliche Zahl gibt es also zwei zugeordnete Zahlen ⇒ keine
eindeutige Zuordnung ⇒ keine Funktion
c)
d)
2) Die abgebildeten Gefäße werden mit gleichmäßig zufließendem Wasser gefüllt. Die Graphen
veranschaulichen den Zusammenhang zwischen Zeit und Füllhöhe des Gefäßes. Ordne die
Gefäße den passenden Graphen zu! Begründe Deine Wahl!
III
I
II
I: Der Zunahme der Füllhöhe ist bei einem Zylinder konstant, Gerade als Graph
II: Zwei unterschiedlich dicke Zylinder, im schmaleren Teil oben nimmt die Füllhöhe schneller zu,
also ist die Steigung des Graphen im zweiten Teil größer.
III: Die Zunahme der Füllhöhe in einem umgedrehten Kegel wird geringer, da der Kegel nach oben
hin breiter wird, Steigung des Graphen ist am Anfang hoch, nimmt dann immer mehr ab.
8.A.2 Lineare Funktionen
1) Bestimme die Schnittpunkte der Funktion y = 3x – 6 mit den Koordinatenachsen!
𝑦 = 0 (Nullstelle)
3𝑥 − 6 = 0
3𝑥 = 6
𝑥 = 2 ⇒ 𝑆𝑥 (2 ∕ 0)
𝑥=0
𝑦 = 3 ⋅ 0 − 6 = −6 ⇒ 𝑆𝑦 (0 ∕ −6)
Dietrich-Bonhoeffer-Gymnasium Oberasbach
2) Zeichne den Graphen von f(x) = ½ x - 3,5 und g(x) = -2,5x + 1 in ein
Koordinatensystem. Bestimme den Schnittpunkt der beiden Graphen
und überprüfe Dein Ergebnis durch Rechnung!
𝑓(𝑥) = 𝑔(𝑥)
1
𝑥 − 3,5 = −2,5𝑥 + 1
2
3𝑥 − 3,5 = 1
3𝑥 = 4,5
𝑥 = 1,5
1
𝑓(1,5) = ⋅ 1,5 − 3,5 = −2,75
2
𝑆(1,5/−2,75)
3) Gib die Zuordnungsvorschrift der linearen Funktion an, die parallel zur x-Achse verläuft und den
Punkt P(1|3) enthält.
Steigung m = 0 => f(x) = 3
4) Ermittle die Funktionsgleichung der linearen Funktion, die durch die Punkte A(-1|4) und B(3|-8)
festgelegt ist.
𝑦2 − 𝑦1
−8 − 4
−12
𝑚=
=
=
= −3
𝑥2 − 𝑥1 3 − (−1)
4
𝑦 = −3𝑥 + 𝑡
𝐴 𝑒𝑖𝑛𝑠𝑒𝑡𝑧𝑒𝑛:
4 = −3 ⋅ (−1) + 𝑡
𝑡=1
𝑓(𝑥) = −3𝑥 + 1
8.A.3 Direkte und indirekte Proportionalität
1) Direkte Proportionalität: 𝑦 = 𝑘 ⋅ 𝑥 ⇒ 𝑘 =
x
20
5
𝑦
𝑥
=
18
20
=
9
10
= 0,9
40
99
y
18
4,5
36
89,1
2) Bestimme die fehlenden Werte der vorliegenden indirekten Proportionalität:
𝑘 = 𝑥 ⋅ 𝑦 = 20 ⋅ 18 = 360
x
20
5
40
27
1
y
18
72
9
13
3
2
9
20
22
3,6
100
3) Entscheide jeweils, ob die Aussage stimmt. Gib bei einer falschen Aussage ein Gegenbeispiel
an!
a) Erhöht sich bei einer direkten Proportionalität die eine Größe um 20, so wird auch die
andere um 20 größer.
Falsch! Erhöhung heißt Zunahme, also Addition (x+20),
Gegenbeispiel: 𝑦 = 3 ⋅ 𝑥, sei 𝑥 = 10 ⇒ 𝑦 = 3 ⋅ 10 = 30
Erhöhung: 𝑥 = 10 + 20 = 30, 𝑦 = 3 ⋅ 30 = 90, y hat sich um 60 erhöht!
b) Verdreifacht sich bei einer direkten Proportionalität die eine Größe, so erhöht sich die
andere um das Doppelte.
Kommt das Doppelte des Ausgangswerts dazu, ist dies eine Verdreifachung! Aussage ist richtig!
Beispiel: Zuordnung Benzinverbrauch v in l → Preis p in € mit 𝑝 = 1,50€ ⋅ 𝑣
v/l
p/€
3
4,50
9
13,50
Dietrich-Bonhoeffer-Gymnasium Oberasbach
c) Halbiert sich bei einer indirekten Proportionalität die eine Größe, so erhöht sich die
andere um 100% ihres Werts.
1
Halbierung bedeutet ⋅ , Erhöhung um 100% heißt Verdopplung, also ⋅ 2 .
2
Aussage ist richtig.
d) Vermindert sich bei einer indirekten Proportionalität die eine Größe um 10, so erhöht
sich die andere um 10.
Aussage ist falsch!
Gegenbeispiel: 360 = 𝑥 ⋅ 𝑦 (Produktgleichheit)
360 = 40 ⋅ 9
360 ≠ 30 ⋅ 19 = 570
8.A.4 Gebrochen-rationale Funktionen und Bruchgleichungen
1
1
 1 . Bestimme ihre
2x  6
2
Definitionsmenge und gib die Gleichungen ihrer waagrechten
und senkrechten Asymptoten an! Skizziere anschließend den
Graphen von f in ein sinnvoll gewähltes Koordinatensystem!
1) Gegeben sei die Funktion f ( x) 
2𝑥 + 6 = 0 ⇒ 𝑥 = −3
⇒ 𝐷 = ℚ\{−3}
Senkrechte Asymptote: 𝑥 = −3
1
Waagrechte Asymptote: 𝑦 = 1 = 1,5
2
2) Gegeben ist der Funktionsgraph einer Funktion der Art
1
g ( x) 
 b (vgl. Abb.1 unten). Bestimme aus der Zeichnung ihre Definitionsmenge und gib
xc
die Gleichungen ihrer waagrechten und senkrechten Asymptote an!
Ermittle dann die Parameter b, c und das richtige Vorzeichen im Zähler des Bruchs!
Senkrechte Asy.: 𝑥 = 1 ⇒ 𝐷 = ℚ\{1} ⇒ 𝑐 = 1
Waagr. Asy.: 𝑦 = 2 ⇒ 𝑏 = 2
Graph befindet sich im 2. Und 4. Quadranten des Asymptotenkreuzes ⇒ negatives Vorzeichen
−1
𝑔(𝑥) =
+2
𝑥−1
1
 1 (vgl. Abb.2 unten). ⇒ 𝐷 = ℚ\{−1}
3) Gegeben ist der Graph der Funktion y 
3x  3
Leider sind in der Zeichnung die Asymptoten und die Koordinatenachsen verschwunden. Zeichne
sie an der richtigen Stelle ein und beschrifte sie passend! (Einheit: 2 Kästchen)
y
4
3
2
1
-2
-1
O
-1
-2
1
2
3 x
Dietrich-Bonhoeffer-Gymnasium Oberasbach
Abb. 1: zu Aufgabe 2
Abb. 2: zu Aufgabe 3
4) Ermittle jeweils die Lösungsmenge der Bruchgleichung!
a)
3
2
5 x  2


2  x x  2 2  x 2  x 
⇒ 𝐷 = ℚ\{−2, 2}
3
−2
−5𝑥 + 2
+
=
2 + 𝑥 (2 − 𝑥) (2 − 𝑥)(2 + 𝑥)
3 ⋅ (2 − 𝑥) − 2(2 + 𝑥) = −5𝑥 + 2
6 − 3𝑥 − 4 − 2𝑥 = −5𝑥 + 2
2 − 5𝑥 = −5𝑥 + 2
−5𝑥 = −5𝑥
⇒ 𝐿 = 𝐷 = ℚ\{−2, 2}
b)
8x  5
1  2 x 2 x  1

1
5

2x 1 2x 1
𝐷 = ℚ\{−0,5; 0,5}
−(8𝑥 − 5)
1(2𝑥 + 1) − 5(2𝑥 − 1)
=
(2𝑥 − 1)(2𝑥 + 1)
(2𝑥 − 1)(2𝑥 + 1)
−8𝑥 + 5 = 2𝑥 + 1 − 10𝑥 + 5
−8𝑥 + 5 = −8𝑥 + 6
5=6
⇒𝐿 ={}
c)
4x  2
2x  2
2 
x 1
2( x  1)
𝐷 = ℚ\{−1}
4𝑥 + 2 2(𝑥 + 1) 2(𝑥 − 1)
−
=
𝑥+1
𝑥+1
2(𝑥 + 1)
4𝑥 + 2 − 2𝑥 − 2 = 𝑥 − 1
2𝑥 = 𝑥 − 1
𝑥 = −1
⇒ 𝐿 = { } , da −1 ∉ 𝐷
8.B Lineare Gleichungssysteme
1) Löse graphisch!
(I)
2x + y = 5 ⇒ 𝑦 = −2𝑥 + 5
(II)
x –y = 1 ⇒𝑦=𝑥−1
⇒ 𝐿 = {(2/1)}
2) Ermittle jeweils die Lösungsmenge!
a)
(I)
(II)
2x + 3y = -2
2x – 8y = 20
c)
(I)
(II)
x=y–4
x = 16 – 3y
⇒ 𝐿 = {(1/5)}
y – 2x = 5
6x + 15 = 3y
⇒ 𝐿 = {(𝑥/𝑦) | 𝑦 = 2𝑥 + 5 }
⇒ 𝐿 = {(2/−2)}
b)
(I)
(II)
d)
(I)
(II)
6y + 7x – 21 = 0
100 – 35x = 30y
⇒𝐿 = {}
Dietrich-Bonhoeffer-Gymnasium Oberasbach
3) Zwei Zahlen unterscheiden sich um 11. Das Quadrat der größeren Zahl ist um 54 kleiner als
das Produkt der Zahlen, die man erhält, wenn man die größere Zahl um 12 verkleinert und
die kleinere Zahl um 45 vergrößert. Wie heißen die beiden Zahlen? Stelle ein
Gleichungssystem auf!
(I)
𝑦 = 𝑥 + 11
(II)
𝑦 2 + 54 = (𝑦 − 12)(𝑥 + 45)
𝐿 = {(10/21)}
4) Die Zehnerziffer einer zweistelligen Zahl ist doppelt so groß wie die Einerziffer. Vertauscht man
die Ziffern, so ist die neue Zahl um 6 größer als die Hälfte der ursprünglichen Zahl. Wie heißt
diese? Stelle ein Gleichungssystem auf!
(I)
(II)
𝑧 =2⋅𝑒
𝑒 ⋅ 10 + 𝑧 − 6 = (𝑧 ⋅ 10 + 𝑒): 2
𝐿 = {(8/4)} Die Zahl heißt 84.
5) Eine Frau verteilt Bonbons unter Kinder. Gibt sie jedem Kind 12 Bonbons, so bleiben 37 Bonbons
übrig. Würde sie aber jedem Kind 15 Bonbons geben, dann fehlten ihr 44 Stück. Wie viele
Bonbons verteilt die Frau an wie viele Kinder? Stelle ein Gleichungssystem auf!
x: Anzahl Kinder
y: Anzahl Bonbons
(I)
(II)
12x = y – 37
15x = y + 44
𝐿 = {(27/361)}
Es sind 27 Kinder und 361 Bonbons.
8.C Strahlensatz
1) Berechne a, b und c! (Skizzen nicht maßstabsgetreu!)
4
8
c
3
a
b
10
2) Berechne jeweils x und y!
Dietrich-Bonhoeffer-Gymnasium Oberasbach
3) Ein Detektiv steht in der Mitte einer Hauseinfahrt verborgen (s. Skizze). Wie viele Meter der
gegenüber liegenden Straßenseite kann er überblicken?
12 m
3m
4m
Er kann 20 m überblicken.
8.D Ähnlichkeit
1)
a) nein; Gegenbeispiel: 1=20°; 1=70°; 1=90° 2=30°; 2=60°; 2=90°
b) nein; Gegenbeispiel: 1=30°; 1=30°; 1=120° 2=50°; 2=50°; 2=80°
c) ja, da alle Winkel in beiden Dreiecken 60° groß sind  ähnlich nach dem Ähnlichkeitssatz
für Dreiecke
d) nein; Gegenbeispiel: 1=1=70°; 1=1=110°
2=2=100°; 2=2=80°
e) nein; Gegenbeispiel: a1=5cm; c1=3cm; h1=2cm; 1=60° a2=5cm; c2=3cm; h2= 2cm; 2=60°
f) nein; Gegenbeispiel; a1=5cm; c1=3cm; h1=2cm;
a2=5cm; c2=3cm; h2=5cm
g) ja
h) ja, da die entsprechenden Winkel in beiden Dreiecken übereinstimmen
i) ja, da alle Winkel gleich groß sind und sie in den Seitenverhältnissen entsprechender Seiten
übereinstimmen
k) nein; Gegenbeispiel: a1=c1=2 cm; b1=d1=5cm a2=c2=3 cm; b2=d2=5cm
l) nein; Gegenbeispiel: Sechseck 1: alle Winkel 120°; Sechseck 2: 5 Winkel 20°, 6. Winkel 620°
m) ja, da alle Winkel gleich groß (120°) und alle Seitenverhältnisse gleich sind (alle Seiten
gleich lang)
2)
a)
50
13
b) hRahmen ≈ 34,6 cm; bRahmen = 62 cm
c) nicht in jedem Fall (s. Teilaufgabe d)
d) Die Rechtecke sind ähnlich, wenn die Seitenverhältnisse gleich sind, d.h. wenn Breite und
Höhe des Rahmen sich 13:9 verhalten.
3) Alle entsprechenden Winkel sind gleich:
∡EDA=∡CBA, da Stufenwinkel
∡AED=∡ACB, da Stufenwinkel
∡DAE=∡BAC
4) Im Dreieck ABC gilt wegen der
Winkelsumme im Dreieck:
α+β+90°=180°,
d.h. α=90°- β
β=90°- α
Das Dreieck AFC hat einen 90°
zu Aufgabe 3
zu Aufgabe 4
Winkel und einen Winkel der
Größe α. Wegen der Winkelsumme muss der dritte Winkel 180°- 90°- α=90°- α = β (s. oben) groß
sein.
Das Dreieck FBC hat einen 90° Winkel und einen Winkel der Größe β. Wegen der Winkelsumme
muss der dritte Winkel 180°- 90°- β=90°- β = α (s. oben) groß sein.
Dietrich-Bonhoeffer-Gymnasium Oberasbach
Damit stimmen alle drei Winkel in den drei Dreiecken überein  ähnlich nach dem
Ähnlichkeitssatz für Dreiecke.
8.E Zufall und Wahrscheinlichkeit
1)
a) Ω={1;2;3;4;5;6;7}
b) P(A)=
1
2
5
3
5
6
; P(B)= ; P(C)= ; P(D)= ; P(E)= ; P(F)=
7
7
7
7
7
7
c) Die Ergebnisse sind nicht mehr gleichwahrscheinlich, da es nun wahrscheinlicher ist eine 5
zu drehen als jede andere Zahl.
2 1
1
; P(5)= 
8
8 4
2 1
2 1
6 3
4 1
6 3
6 3
e) P(A)=  ; P(B)=  ; P(C)=  ; P(D)=  ; P(E)=  ; P(F)= 
8 4
8 4
8 4
8 2
8 4
8 4
d) P(1)= P(2)= P(3)= P(4)= P(6)= P(7)=
2)
Mädchen
Junge
a)
Latein
8
8
16
18
30
b)
Französisch
4
10
14
8
30
c)
12
18
30
10
30
d)
14
30
3)
a) |Ω|=2⋅ 6⋅ 6=72
b)
24
72
18
72
c)
d)
12
72
e)
36
72
f)
18
36
g)
72
72
4)
a) 6!=720
b) 3!⋅ 2=12
c) 3!⋅ 3!=36
d) 4⋅ 3!⋅ 3!=144
e) 4!=24
f) 4⋅ 3!=24
8.F Potenzen mit ganzzahligen Exponenten
1)
a) 23000m=2,3⋅ 104m b) 50000cm=5,0⋅ 104cm
e) 23000m2=2,3⋅ 104m2 f) 0,47m=4,7⋅ 10-1m
i) 3600000g=3,6⋅ 106g k) 0,00001hl=1⋅ 10-5hl
c) 12000l=1,2⋅ 104l
d) 36000m2=3,6⋅ 104m2
-4
g) 0,00056km=5,6⋅ 10 km h) 0,64l=6,4⋅ 10-1l
l) 8,2a
m) 0,00037g=3,7⋅ 10-4g
2)
3
x
8
a) x 7
b)
a) 26  64
b) 2  6 
g)  8a 6
h)
a) 216a 3
b) 16a 2
c) 
1 1
x
12
d) 6b3  12
e) 24a 3b  16a 2  0,5a 1b3
d)  8a 3
e)
k) 56
l) 50 3
d)  3a 2 x 6
e) a 2  8a  16
3)
1 6
a
8
1
1
c) 2  6 
64
64
i)
36 729

64
26
1
8a 3
f)  4a 6
m) 253
4)
g) 4a 2  12a  9
c) 4a 6
h) 36a 2 i)  3a 6 x 3
k)
1
a  2ab  b 2
2
f)
1
x3
l) 8  12b  6b2  b3
Dietrich-Bonhoeffer-Gymnasium Oberasbach
3)
a) x 5
b) x
e) 0,11  10
f) 1
i) 16a 4
k) 35 x
5 2
x
6
5 2
g)
a
2
d) 4a 2b
c)
h) 3a 3
4)
a)
y 3z 4
x2
b5 c 3
b5
 x3y 4
1
c)

 3
6 4
7 4
7
x y
x
a c
a c
b)
d)
b2
16a 6
e)
27a 2bc 2
3c 2

36a5b3
4a 3b 2
8.G Berechnungen am Kreis
1) Die schraffierten Flächen haben allen den Flächeninhalt a 2 
1 2
a 
4
2)
1
(3cm)2   (1,5cm)2   2,25 cm2 ;
2
1
b) A  (3cm)2   4,5 cm2 ;
2
c) A  (2cm)2   (1cm)2   3 cm2
1
d) A  (3cm)2   4,5 cm2
2
a) A 
3)
1
 2  3cm    2  1,5cm    6 cm
2
1
U   2  3cm    2  1,5cm    6 cm
2
U  2  2cm    2  1cm    6 cm
1
U   3cm    2  2  1,5cm    7,5 cm
2
U
1
1
(3,5cm)2   (2,5cm)2  0,5 cm2
12
12
1
1
U
 2  3,5cm   
 2  2,5cm    2cm  1 cm  2cm  5,14 cm
12
12
A
4)
Tag
Tag 1
zur Verfügung stehende Fläche
(2m)   4 m2 = eine Tagesration
Tag 2
(3m)2   (2m)2   5 m2
Tag 3
(4m)2   (3m)2   7 m2
Tag 4
(5m)2   (4m)2   9 m2
Tag x
x2
(2m  xm)2   (1m  xm)2   (3  2x) m2
2
(3  2 x) m2  4 m2
3  2x
4
x  0,5
Gustav wird an jedem Tag satt, da die zur Verfügung stehende Fläche ab dem 2. Tag immer
größer als die Tagesration ist.
5)
URiesenpizza  2  17,5cm    109,9cm
Die Pizza ist 9% kleiner als angegeben.