Ein- und zweidimensionale Stöße mit Computersimulation

Ein- und zweidimensionale Stöße
mit
Computersimulation
Die in dieser Arbeit vorgestellte Physik behandelt Stoßvorgänge in ein- und
zweidimensionalen Systemen. Die Betrachtung erfolgt dabei nur vereinfacht und
modellhaft, gibt jedoch einen guten Einblick über die Vorgänge bei realen
Stoßvorgängen, wie sie zum Beispiel beim Billardspiel auftreten.
Dass in der Physik eine vereinfachte Betrachtung komplizierter Vorgänge sinnvoll sein
kann, ist sehr gut an der kinetischen Gastheorie zu erkennen. In dieser Theorie werden
die Kollisionen einzelner Gasteilchen auf eindimensionale Stoßvorgänge abstrahiert.
Aber auch die komplexen Stoßvorgänge des Billardspiels können mit dem Modell des
zweidimensionalen Stoßes schon recht genau vorherberechnet werden.
Inhaltsverzeichnis
Kapitel:
Seite:
1. Physikalische Betrachtung ein- und zweidimensionaler Stöße
1.1. Impuls und Definition der Impulsgröße
1.2. Beziehung zwischen Impuls und Kraft
1.3. Definition und Herleitung des Kraftstoßes
1.4. Die wichtigen Erhaltungsgrößen in der Physik
3
3
4
5
1.4.1. Begriff des abgeschlossenen Systems
1.4.2. Energieerhaltungssatz
1.4.3. Impulserhaltungssatz
5
5
5
1.5. Einteilung und Behandlung der verschiedenen Stoßarten
1.5.1. Merkmale des zentralen Stoßes
1.5.2. Merkmale des exzentrischen Stoßes
1.5.3. Behandlung des vollelastischen Stoßes
1.5.4. Behandlung des unelastischen Stoßes
1.5.5. Behandlung des wirklichen Stoßes
1.6. Sonderfälle bei Stoßvorgängen
1.6.1. Zentraler elastischer Stoß zweier Körper gleicher Masse
1.6.2. Senkrechter elastischer Stoß eines Körpers auf eine Wand
1.6.3. Schiefer elastischer Stoß eines Körpers auf eine Wand
1.7. Zweidimensionaler Stoß zwischen zwei Kugeln
1.7.1. Ausgangsbedingungen
1.7.2. Vektorielle Kräftedarstellung und Zerlegung
1.7.3. Mathematische Behandlung der Kräfte
6
6
7
7
9
10
10
10
11
11
12
12
12
13
2. Erläuterung bestimmter Quellcodeausschnitte
2.1. Klasse „VECTOR2“ als Kapselung der Vektormathematik
2.2. Verwaltung der Kugeln in einem Listenobjekt
2.3. Berechnung der Simulationsphysik
2.3.1. Kollision einer Kugel mit einer Wand
2.3.2 Kollisionserkennung zwischen zwei Kugeln
2.3.3 Kollisionsberechnungen
2.4. Verwaltung der Kollisionen in einer Zeittabelle
14
15
16
16
17
18
19
3. Anhang
3.1. Quellcode zum Simulationsprogramm
3.2. Inhalt der beigelegten CD-Rom
3.3. Separate Anleitung zum Simulationsprogramm
3.4. Ausdruck der Internetquellen
3.5. Quellenangaben
3.6. Schlusserklärung
20
20
20
20
21
21
-3-
1. Betrachtung ein- und zweidimensionaler Stöße
1.1. Impuls und Definition der Impulsgröße
Der Impuls ist eine physikalische, vektorielle Größe, die der Bewegung eines
Massepunktes zugeordnet werden kann. Jeder bewegte und Masse besitzende Körper
trägt daher einen Impuls. Er kann diesen bei Stößen und anderen Wechselwirkungen
teilweise oder ganz an andere Körper übertragen1.
Der Impuls ist definiert als Produkt von Masse ( m ) und Geschwindigkeit ( v ) eines
Körpers:
p = mv
Die Einheit des Impulses im SI ist
kgm kgm
=
s = Ns . Die Einheit Newtonsekunde (Ns)
s
s²
kann auch unter dem Namen „Huygens“ und dem Einheitenzeichen „Hy“ vorkommen2.
1.2. Beziehung zwischen Impuls und Kraft
Eine auf einen Körper wirkende Kraft F ändert den Impuls p dieses Körpers. Dabei ist
die Impulsänderung pro Zeit gleich der auf den Körper wirkenden Kraft. Dies ist das
zweite Newtonsche Axiom3.
d d F = p → mv
dt
dt
d Bei konstanter Masse also F = m v .
dt
Die Ableitung der Geschwindigkeit v nach der Zeit ist die Beschleunigung a .
F = ma
1
Wikipedia – Impuls (Physik) – Quelle 8
Wikipedia – Impuls (Definition und Bedeutung) – Quelle 8
3
Wikipedia – Impuls (Impuls und Kraft) – Quelle 8
2
-4-
1.3. Definition und Herleitung des Kraftstoßes
Abb. 1: Anstoß einer Billardkugel mit dem Queue als Beispiel für einen Kraftstoß4
Ein Kraftstoß findet statt, wenn in einem geschlossenen System der Impuls durch eine
Krafteinwirkung von außen geändert wird5.
F = ma mit einer konstanten Beschleunigung im Zeitraum △t gilt:
△v
F=m
→△p = m△v
△t
hierbei ist △v die Geschwindigkeitsänderung, die der Körper durch die Krafteinwirkung
erfährt, also die Differenz aus der Geschwindigkeit vor und nach dem Kraftstoß6.
I =△p = F△t
4
http://www.billard-henzgen.de
Wikipedia – Kraftstoß – Quelle 7
6
Wikipedia – Kraftstoß (Herleitung) – Quelle 7
5
-5-
1.4. Die wichtigen Erhaltungsgrößen in der Physik
1.4.1. Begriff des abgeschlossenen Systems
„Als abgeschlossenes System bezeichnet man eine räumlich begrenzte Anordnung von
Körpern, die untereinander in Wechselwirkung stehen, ohne dass die Körper von
außerhalb des Systems durch Impulsaustausch oder Ähnlichem beeinflusst werden“7.
1.4.2. Energieerhaltungssatz
In einem abgeschlossenen System ist die Summe der mechanischen Energien konstant,
solange die Vorgänge im System reibungslos verlaufen.
E = E kin + E pot = const.
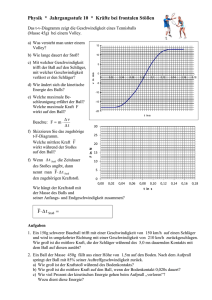
In Abbildung zwei ist der Energieverlauf der kinetischen Energie (blau) und der
potentiellen Energie (gelb) beim freien Fall zu sehen. Dabei wird die potentielle Energie
immer weiter verlustfrei in kinetische Energie umgewandelt, so dass die Gesamtenergie
zu jedem Zeitpunkt konstant bleibt.
Abb. 2: Energieverlauf beim freien Fall8
1.4.3. Impulserhaltungssatz
In einem abgeschlossenen System ist die (vektorielle) Summe der Impulse zeitlich
konstant9.
m1 v1 + m 2 v2 + m3 v3 + ... + m n v n = const.
p1 + p2 + p3 + ... + p n = const.
7
METZLER – Seite 43 – Quelle 1
METZLER – Seite 79 – Quelle 1
9
Physikalische Formeln – Seite 15 – Quelle 4
8
-6-
1.5. Einteilung und Behandlung der verschiedenen Stoßarten
Ein Stoß liegt dann vor, wenn sich zwei Körper während eines sehr kleinen
Zeitabschnittes △t berühren und dabei ihre Geschwindigkeiten ändern. Während der
Berührungszeit △t erfahren beide Körper den Kraftstoß F△t 10.
Die Tangentialebene verläuft durch den Berührungspunkt der beiden Körper zu Beginn
des Stoßes. Die Stoßnormale ist die Wirklinie der beiden Normalkräfte, die während des
Stoßvorganges auf beide Körper wirkt. Sie verläuft senkrecht zur Tangentialebene.
(siehe dazu Abbildung 3).
1.5.1. Merkmale des zentrischen Stoßes
Geht die Stoßnormale durch die Schwerpunkte beider Stoßpartner, so spricht man von
einem zentrischen Stoß.
Liegen die beiden Geschwindigkeitsvektoren v1 und v2 zu Beginn des Stoßes parallel
zur Stoßnormalen vor, so handelt es sich zusätzlich noch um einen geraden Stoß.
Abb. 3: Skizze eines zentrischen Stoßes mit eingezeichneter Stoßnormaler11
10
11
Technische Mechanik – Seite 224 – Quelle 2
Technische Mechanik – Seite 224 – Quelle 2
-7-
1.5.2. Merkmale des exzentrischen Stoßes
Geht die Stoßnormale nicht durch die Schwerpunkte beider Stoßpartner, so liegt ein
exzentrischer Stoß vor.
Liegen zusätzlich noch die beiden Geschwindigkeitsvektoren v1 und v2 zu Beginn des
Stoßes nicht parallel zur Stoßnormalen, so liegt ein schiefer exzentrischer Stoß vor.
1.5.3. Behandlung des vollelastischen Stoßes
Abb. 4: Energiebilanz beim vollelastischen Stoß12
Beim elastischen Stoß verhalten sich die Körper federnd. Das heißt, nach dem Stoß sind
alle Verformungen wieder vollkommen zurückgegangen. Äußere und innere Reibung
werden beim elastischen Stoß vollständig vernachlässigt13. Der elastische Stoß läuft also
in einem abgeschlossenen System ab und es gilt sowohl die Impulserhaltung als auch
die Energieerhaltung.
Der Vorgang kann leichter verfolgt werden, wenn man ihn in zwei Teilabschnitte
unterteilt.
Erster Stoßabschnitt (Zusammendrücken):
Der erste Stoßabschnitt beginnt mit der Berührung der zwei Stoßkörper und endet, wenn
der Abstand der beiden Körper lmin erreicht hat. In diesem Moment liegt die stärkste
Verformung der zwei Körper vor. Diese Verformung hat ihre Energie aus der
12
13
Technische Mechanik – Seite 225 – Quelle 2
Technische Mechanik – Seite 225 – Quelle 2
-8Geschwindigkeit des schnelleren Körpers erhalten. Nun haben also beide Körper die
gleiche Geschwindigkeit c .
Aus dem Impulserhaltungssatz folgt nun:
Vor dem Stoß:
nach dem ersten Stoßabschnitt:
m1v1 + m 2 v 2 = m1c + m 2 c
Daraus erhält man die Geschwindigkeit c beider Körper nach dem ersten Stoßabschnitt:
c=
m1v1 + m 2 v 2
m1 + m 2
(1)
Zweiter Stoßabschnitt (Entspannen):
Der zweite Stoßabschnitt beginnt beim Minimalabstand lmin und endet bei der
vollständigen Trennung der beiden Körper.
Die in der Verformung der Körper gespeicherte Spannungsenergie wird nun verlustfrei
abgegeben. Der Kraftstoß beim Verformen (erster Stoßabschnitt) ist also gleich dem
Kraftstoß beim Freisetzen der Spannungsenergie (zweiter Stoßabschnitt)14.
Daraus folgt nun, dass die Geschwindigkeitsänderung von v1 / v 2 zur gemeinsamen
Geschwindigkeit c gleich der Änderung von c auf die Endgeschwindigkeiten c1 / c2 ist.
v1/ 2 − c = c − c1/ 2
(2)
Aus (1) und (2) erhält man die Gleichungen für den vollelastischen, zentrischen Stoß
zweier Körper15:
c1 =
(m1 − m 2 )v1 − 2m 2 v 2
m1 + m 2
c2 =
(m 2 − m1 )v 2 + 2m1v1
m1 + m 2
Es gilt zu beachten, dass v1 und v 2 , sowie die Ergebnisse c1 / c2 skalare Werte sind.
14
15
Technische Mechanik – Seite 225 – Quelle 2
Physikalische Formeln – Seite 16 – Quelle 4
-9-
1.5.4. Behandlung des unelastischen Stoßes
Abb. 5: Beziehung zwischen Stoßenergie und Verformungsarbeit16
„Unelastische Körper verformen sich beim Stoß plastisch. Sie erhalten also eine
bleibende Formänderung“17.
Erster Stoßabschnitt:
Der erste Stoßabschnitt erfolgt wie beim elastischen Stoß. Am Ende besitzen beide
Körper die gemeinsame Geschwindigkeit c. Die Formänderungsarbeit ist jedoch nicht
als Spannungsenergie gespeichert, sondern wurde in Wärme umgesetzt18.
Zweiter Stoßabschnitt:
Der zweite Stoßabschnitt entfällt beim unelastischen Stoß vollkommen, da keine
gespeicherte Spannungsenergie vorliegt. Es erfolgt also keine Trennung der beiden
Körper nach dem Stoß, da sich beide mit der Geschwindigkeit c weiterbewegen.
Die Endgeschwindigkeit c für beide Körper erhält man analog zur Geschwindigkeit
beider Körper am Ende des ersten Stoßabschnittes des elastischen zentrischen Stoßes:
m1v1 + m 2 v 2
c=
m1 + m 2
16
Technische Mechanik – Seite 227 – Quelle 2
Technische Mechanik – Seite 227 – Quelle 2
18
Technische Mechanik – Seite 227 – Quelle 2
17
- 10 -
1.5.5. Behandlung des wirklichen Stoßes
Die Formänderungsarbeit wird im zweiten Stoßabschnitt nicht vollständig
zurückgegeben, sondern teilweise in Wärme umgewandelt.
Abb. 6: Energieverlust beim wirklichen Stoß durch Wärmeabgabe19
1.6. Sonderfälle bei Stoßvorgängen
1.6.1. Zentraler elastischer Stoß zweier Körper gleicher Masse
Bei diesem Sonderfall des zentralen elastischen Stoßes haben beide Stoßpartner die
gleiche Masse. Also gilt:
m1 = m 2 = m
Setzt man dies nun in die zwei Gleichungen des zentralen elastischen Stoßes ein, so
erhält man:
c1 = v 2 und c 2 = v1
Körper mit gleicher Masse tauschen ihre Impulse gegenseitig aus20:
p1 ' = p 2
19
20
und
p 2 ' = p1
Technische Mechanik – Seite 229 – Quelle 2
METZLER – Seite 43 – Quelle 1
- 11 -
1.6.2. Senkrechter elastischer Stoß eines Körpers auf eine Wand
Beim senkrechten elastischen Stoß auf eine Wand, nimmt man an, dass die Masse des
Stoßkörpers sehr klein gegenüber der Masse der Wand ist ( m1 << m 2 ). Dadurch erhält
man aus der normalen Gleichung für den zentralen elastischen Stoß folgenden
Zusammenhang: c1 = 2v 2 − v1
Da sich die Wand aufgrund ihrer großen Masse nicht bewegt,
kann man v 2 = 0 setzen und erhält so21:
c1 = − v1 und v 2 = 0
Die Geschwindigkeitsänderung des Stoßkörpers ist damit: △ v = v1 − (− v1 ) = 2v1
Der Kraftstoß auf die Wand ist also: I =△p = 2m1v1
Dem Betrag nach ist die Impulsänderung also doppelt so groß wie der Impuls vor oder
nach dem Stoß.
1.6.3. Schiefer elastischer Stoß eines Körpers auf eine Wand
Abb. 7: Vektordarstellung eines schiefen elastischen Stoßes mit einer Wand22
Die Komponente des Impulses, die
parallel zur Wand liegt, bleibt unverändert:
p par ' = p par
Für die senkrechte Komponente des Impulses gilt
analog zum senkrechten elastischen Stoß mit einer Wand:
Für den elastischen Stoß auf eine Wand gilt das
Reflexionsgesetzt der Optik:
21
22
METZLER – Seite 43 – Quelle 1
METZLER – Seite 43 – Quelle 1
psenk ' = − psenk
ppar = p ⋅ cos ( α )
psenk = p ⋅ sin ( α )
- 12 -
1.7. Zweidimensionaler Stoß zwischen zwei Kugeln
1.7.1. Ausgangsbedingungen
Abb. 8: Übersicht über die Lage der Geschwindigkeitskomponenten beim zweidimensionalen Stoß23
Beim zweidimensionalen Stoß zweier Kugeln handelt es sich um einen schiefen
zentrischen Stoß zweier Körper.
Bei diesem liegen die Geschwindigkeitsvektoren der beiden Stoßkörper ( v1 | v 2 ), nicht
entlang der Stoßnormalen (also nicht senkrecht zur Tangentialebene).
1.7.2. Vektorielle Kräftedarstellung und Zerlegung
Als erstes müssen die Geschwindigkeiten in eine Komponente parallel, also in Richtung
der Stoßnormalen ( v p ) und in eine Komponente senkrecht zur Stoßnormalen ( vs )
zerlegt werden.
Nun kann der Stoß als eindimensional, also als zentrisch und gerade betrachtet werden,
indem man nur die parallele Komponente weiter berücksichtig und die senkrechte
Komponente unverändert lässt.
Man berechnet die neue parallele Komponente genauso wie beim zentrischen geraden
elastischen Stoß (siehe 1.5.3. Behandlung des vollelastischen Stoßes). Der
Unterscheidung zwischen Vektoren und Skalaren muss besondere Beachtung geschenkt
werden.
23
The Math and Physics of Billards – Quelle 6
- 13 -
1.7.3. Mathematische Behandlung der Kräfte
Abb. 9: Vektorzerlegung
Um die Betrachtung einfach zu halten, bewegt sich
in diesem Beispiel vor dem Stoßvorgang nur die
Kugel k1 . Die Berechnung der Endgeschwindigkeit
beschränkt sich ebenfalls auf die erste Kugel. Die
Werte der zweiten Kugel können jedoch analog zur
ersten berechnet werden. (Mit vsenk / csenk und
v par / c par sind im Folgenden also immer die
Geschwindigkeitskomponenten der ersten Kugel
gemeint).
Zum Zerlegen der Geschwindigkeiten in die einzelnen Komponenten, berechnet man als
erstes die Stoßnormale n 0 . Diese erhält man, indem man den Verbindungsvektor der
beiden Kugeln k1k 2 auf die Länge 1 normiert24.
0
k 1k 2
k 1 k 2 = k 2 − k 1 → n = | k 1k 2 |
 0 
v n
α = cos −1  1 
0
 v1 n 


Als nächstes kann man den Winkel α zwischen dem
Geschwindigkeitsvektor v1 und der Stoßnormalen
n 0 mit Hilfe des Skalarproduktes berechnen25:
Mit Hilfe des Winkels α und den Winkelfunktionen
0
v par = v1 n cos ( α )
kann man nun die parallele Komponente der
Geschwindigkeit berechnen.
Die senkrechte Komponente erhält man
nun durch Vektorsubtraktion:
vsenk = v1 − v par
Den Betrag der neuen parallelen Komponente
erhält man mit der Gleichung für den
c par =
(m1 − m 2 ) | v par |
m +m
1
2
eindimensionalen zentrischen geraden Stoß:
0
Daraus folgt dann: c par = cpar v par und mit Vektoraddition die Endgeschwindigkeit:
c1 = cpar + vsenk
24
25
The Math and Physics of Billards – Quelle 6
Mathematische Formeln – Seite 79 – Quelle 5
- 14 -
2. Erläuterung bestimmter Quellcodeausschnitte
2.1. Klasse „VECTOR2“ als Kapselung der Vektormathematik
Die Klasse „VECTOR2“ dient der Kapselung der Mathematik von zweidimensionalen
Vektoren. Dazu bietet sie Methoden zum Erstellen und Rechnen mit Vektoren.
Quellcode 1: C_Vector.h (Zeile: 8 - 26)
class VECTOR2
{
public:
VECTOR2();
VECTOR2(float x,float y); // Erstellt einen Vektor mit x und y Komponente
~VECTOR2();
float CompX(void); // x Komponente erhalten
float CompY(void); // y Komponente erhalten
void Set(float x,float y); //x und y Komponente setzen
VECTOR2 operator + (VECTOR2 v); // Addieren von zwei Vektoren
VECTOR2 operator - (VECTOR2 v); // Subtrahieren von zwei Vektoren
VECTOR2 operator * (float fValue); //Multiplikation des Vektors mit einem Skalar
float operator * (VECTOR2 v); // Skalar-Produkt zweier Vektoren (liefert ein Skalar)
float Amount(void); // Betrag eines Vektors
VECTOR2 Normalize(void); // Liefert den Einheitsvektor
protected:
float x; // x Komponente
float y; // y Komponente
};
Durch das Überladen der Operatoren können die Klassenobjekte mit den Operatoren
“+,-,*” untereinander mathematisch verknüpft werden.
Quellcode 2: Beispielcode
// Erstellen von zwei Vektorobjekten
VECTOR2 v1(5.0f,5.0f);
VECTOR2 v2(10.0f,10.0f);
// Addieren der Vektoren mit Hilfe des überladenen Operators „+“
VECTOR2 vResult = v1+v2;
- 15 -
2.2. Verwaltung der Kugeln in einem Listenobjekt
Die Eigenschaften der Kugeln werden in der Struktur „S_Ball“ gespeichert.
Quellcode 3: main.cpp (Zeile: 75 - 90)
// Verwaltung der Kugeleigenschaften
struct S_Ball
{
float x,y; // x und y Komponente des Ortsvektors
float vx,vy; // x und y Komponente des Geschwindigkeitsvektors
int fMass; // Masse der Kugel
int fSize; // Durchmesser der Kugel in Pixel
int iID; // interne ID der Kugel
char cName[128]; // Name der Kugel (max. 128 Zeichen)
int iColor; // Farbwert der Kugel
S_Ball() // Standart-Konstruktor
{
// Alle Variablen auf Standartwerte setzen
x=0;y=0;vx=0;vy=0;fMass=100;fSize=20;iColor=5;
}
};
Eine neue Kugel wird erstellt indem zuerst ein „S_Ball“ Objekt erstellt wird und dieses
mit passenden Werten für die einzelnen Variablen versehen wird. Als nächstes wird
eine Kopie des „S_Ball“ Objektes im Listen-Objekt „BallList“ gespeichert.
Quellcode 4: main.cpp (Zeile: 1772 - 1787)
// Neue Kugel erstellen
S_Ball Ball;
// uniqueID zuweisen
Ball.iID = iCurrID;
// Verfügbare IDs aktualisieren
iCurrID++;
// Namen der Kugel an ID anpassen
char *pBuffer = Ball.cName;
sprintf(pBuffer,"Kugel %d",Ball.iID);
// Position der Kugel auf Simulationsfenstermitte setzen
RECT r = {0,0,0,0};
GetClientRect(hRenderWnd,&r);
Ball.x = r.right/2;
Ball.y = r.bottom/2;
// Ball der Liste hinzufügen
AddBall(&Ball);
- 16 Ein Zugriff auf die einzelnen Kugeln ist nun über das „BallList“ Listen-Objekt möglich:
Quellcode 5: Beispielcode
// Globales Listen-Objekt
std::list<S_Ball>BallList;
// Iterator für das Listen-Objekt
// Mit dem Iterator kann ein Zugriff auf die in der Liste gespeicherten Objekte erfolgen
std::list<S_Ball>::iterator it;
// Liste der Reinfolge nach durchgehen
for(it=BallList.begin();it!=BallList.end();it++)
{
// Zugriff auf das Objekt an der aktuellen Listenposition
it->ObjektZugriff();
}
2.3. Berechnung der Simulationsphysik
2.3.1. Kollision einer Kugel mit einer Wand
Quellcode 6: main.cpp (Zeile: 964 - 968)
// r.right ist die Breite des Fensterbereiches
// r.bottom ist die Höhe des Fensterbereiches
// it ist der Zugriffsiterator für die BallList, und somit zu den einzelnen Kugeln
if(it->x-it->fSize/2 < 15){it->vx = it->vx*-1;}
if(it->y-it->fSize/2 < 15){it->vy = it->vy*-1;}
if(it->x+it->fSize/2+15 > r.right){it->vx = it->vx*-1;}
if(it->y+it->fSize/2+15 > r.bottom){it->vy = it->vy*-1;}
Es wird überprüft, ob die aktuelle Position der Kugel noch innerhalb des
Simulationsfensterbereiches ist. Wenn die Kugel die obere oder untere Bande
überschritten hat, wird die Y-Komponente der Kugelgeschwindigkeit umgekehrt.
Wenn die Kugel dagegen die linke oder rechte Bande überschritten hat, wird die XKomponente der Kugelgeschwindigkeit umgekehrt. (siehe 1.6.3. Schiefer elastischer
Stoß eines Körpers auf eine Wand).
- 17 -
2.3.2 Kollisionserkennung zwischen zwei Kugeln
Quellcode 7: main.cpp (Zeile: 980 - 989)
// it ist wiederum der Iterator für die BallList und erlaubt Zugriff auf die Kugeleigenschaften
// Vektoren für die 2 Kugeln erstellen
VECTOR2 Vb1(it->x+it->vx,it->y+it->vy);
VECTOR2 Vb2(er->x+er->vx,er->y+er->vy);
// Verbindungsvektor erstellen und berechnen
VECTOR2 Vt;
Vt = Vb1-Vb2;
// Wenn der Betrag des Verbin.Vektors kleiner als der Radius
// dann liegt eine Kollision vor
if(Vt.Amount() < (it->fSize+er->fSize)/2)
{
// Kollision berechnen
}
// VECTOR2:: Amount() liefert den Betrag des Vektors
Zuerst wird der Verbindungsvektor der Ortsvektoren der zwei Kugeln berechnet. Ist der
Betrag, also die Länge dieses Verbindungsvektors, kleiner als Summe der Kugelradien,
so liegt eine Kollision der zwei Kugeln vor.
Abb.10: Kollisionserkennung bei zwei Kugeln
- 18 -
2.3.3 Kollisionsberechnungen
Quellcode 8: main.cpp (Zeile: 2723 - 2777)
// Ball1 und Ball2 sind Zeiger auf die an der Kollision beteiligten Kugelobjekte
// Vektor für Kugel 1 erstellen
VECTOR2 k1(Ball1->x,Ball1->y);
VECTOR2 v1(Ball1->vx,Ball1->vy);
// Vektor für Kugel 2 erstellen
VECTOR2 k2(Ball2->x,Ball2->y);
VECTOR2 v2(Ball2->vx,Ball2->vy);
// Verbindungsvektor der zwei Kugeln ist die Stoßnormale
VECTOR2 n = (k2-k1);
// Winkel zwischen Kugel1 und Stoßnormaler
float f1 = (v1*n)/(n*n);
// Paralelle Komponente
VECTOR2 vp1 = n*f1;
// Senkrechte Komponente
VECTOR2 vs1 = v1-vp1;
// Winkel zwischen Kugel2 und Stoßnormaler
float f2 = (v2*n)/(n*n);
// Parallele Komponente
VECTOR2 vp2 = n*f2;
// Senkrechte Komponente
VECTOR2 vs2 = v2-vp2;
// Wenn Massen der zwei Kugeln gleich sind -> Vereinfachung
// Parallele Komponenten werden getauscht, senkrechte bleiben gleich
if(Ball1->fMass == Ball2->fMass)
{
v1 = vs1+vp2;
v2 = vs2+vp1;
// in Geschwindigkeitskomponenten aufteilen
Ball1->vx = v1.CompX();
Ball1->vy = v1.CompY();
Ball2->vx = v2.CompX();
Ball2->vy = v2.CompY();
}
else
{
// wenn Masse nicht gleich, dann: Vsenkrecht bleibt gleich
// Vparalell mit Impulssätzen
float v1x = elStoss(Ball1->fMass,vp1.CompX(),Ball2->fMass,vp2.CompX());
float v1y = elStoss(Ball1->fMass,vp1.CompY(),Ball2->fMass,vp2.CompY());
VECTOR2 vn1(v1x,v1y);
float v2x = elStoss(Ball2->fMass,vp2.CompX(),Ball1->fMass,vp1.CompX());
float v2y = elStoss(Ball2->fMass,vp2.CompY(),Ball1->fMass,vp1.CompY());
VECTOR2 vn2(v2x,v2y);
v1 = vs1+vn1;
v2 = vs2+vn2;
// in Geschwindigkeitskomponenten aufteilen
Ball1->vx = v1.CompX();
Ball1->vy = v1.CompY();
Ball2->vx = v2.CompX();
Ball2->vy = v2.CompY();
}
- 19 -
2.4. Verwaltung der Kollisionen in einer Zeittabelle
Wenn sich zwei Kugeln nach einer Kollisionsberechnung nicht sofort vollständig
voneinander lösen, wird von der Simulation fälschlicherweise eine erneute Kollision
erkannt. Dieser Effekt tritt vor allem bei sehr großen Streuwinkeln auf. Um dieses
Problem zu umgehen, beachtet die Simulation nur Kollisionen zweier Kugeln, die von
der letzen Kollision genau dieser zwei Kugeln einen bestimmten Zeitwert entfernt
liegen.
Im Programm wird hierzu eine Zeittabelle angelegt, die alle Kollisionen zusammen mit
ihrem genauen Zeitpunkt abspeichert. Tritt nun eine Kollision auf, wird in der
Zeittabelle abgelesen, ob die Kollision beachtet werden muss. Dazu wird der
gespeicherte Zeitwert mit dem aktuellen Zeitwert verglichen und somit geprüft ob die
letzte gespeicherte Kollision bereits lange genug vergangen ist.
Quellcode 9: main.cpp (Zeile: 2687 - 1722)
bool PhCheckTimeTable(int iID1,int iID2)
{
// iID1 ist die ID der ersten Kugel die an der Kollision beteiligt ist
// iID2 ist die ID der zweiten Kugel die an der Kollision beteiligt ist
// TimeList ist die Zeittabelle in der die Werte gespeichert liegen
for(tt=TimeList.begin();tt!=TimeList.end();tt++) // Zeittabelle wird durchgegangen
{
// Wenn für die zwei Kugeln, die an der Kollision
// beteiligt sind, ein Eintrag in der Tabelle vorhanden ist
if((tt->iID1==iID2&&tt->iID2==iID2)||(tt->iID2==iID1&&tt->iID1==iID2))
{
// Wenn der Eintrag älter als iWaitTime ist
if(GetTickCount() > (tt->iTime+iWaitTime))
{
tt->iTime = GetTickCount(); // neuen Eintrag erstellen
return true; // Kollision erkennen und später berechnen
}
// Wenn der Eintrag nicht lange genug her ist
else
{
return false; // Kollision übergehen und nicht berechnen
}
}
}
// Wenn noch kein Eintrag in der Tabelle vorhanden war neuen Eintrag erstellen
S_Time Time;
Time.iID1 = iID1; // ID der ersten Kugel
Time.iID2 = iID2; // ID der zweiten Kugel
Time.iTime = GetTickCount(); // "Uhrzeit", zu der der Eintrag erstellt wurde
TimeList.push_back(Time); // Speichern des Eintrages in der Tabelle
return true; // Kollision erkennen und später berechnen
}
- 20 -
3. Anhang
3.1. Quellcode zum Simulationsprogramm
Der Quellcode zum Simulationsprogramm besteht aus den Dateien „C_Vector.h“,
„C_Vector.cpp“, „resource.h“ und „main.cpp“. Die Dateien befinden sich im
Verzeichnis „\Simulation\Quellcode\“ auf der beiligenden CD-Rom. Es ist kein
Ausdruck des Quellcodes beigelegt, da dieser insgesammt über 3000 Zeilen beinhaltet.
3.2. Inhalt der beigelegten CD-Rom
Auf der beigelegten CD-Rom befinden sich:
- eine digitale Version der Facharbeit als pdf-Datei
- eine digitale Version der Anleitung als pdf-Datei
- die Simulation als ausführbare Datei
- der Quellcode des Simulationsprogramms
- VC++ 6.0 zum kompilieren der Quellcodedateien
- Acrobat Reader zum Öffnen der pdf-Dateien
3.3. Separate Anleitung zum Simulationsprogramm
Die Anleitung zum Simulationsprogramm ist sowohl als digitale Version auf der CDRom, als auch als separater Ausdruck der Facharbeit beigelegt.
3.4. Ausdruck der Internetquellen
Die verwendeten Internetquellen (siehe 3.5 Quellenangaben) liegen in ausgedruckter
Form dem Anhang bei.
- 21 -
3.5. Quellenangaben
Literaturquellen:
1) METZLER – Physik 3.Auflage (Joachim Grehn und Joachim Krause)
2) VIEWEG - Technische Mechanik (Alfred Böge)
3) HARRI DEUTSCH - Vorlesungen über Theoretische Physik I (Arnold Sommerfeld)
4) J.LINDAUER – Physikalische Formeln und Tabellen (Hammer und Hammer)
5) J.LINDAUER – Mathematische Formeln und Tabellen (Barth, Wörle und Nikol)
Internetquellen:
6)
The Math and Physics of Billards
http://archive.ncsa.uiuc.edu/Classes/MATH198/townsend/math.html
7)
Wikipedia – Kraftstoß (Version vom 16. Dezember 2006)
http://de.wikipedia.org/wiki/Kraftsto%C3%9F
8)
Wikipedia – Impuls (Physik)
http://de.wikipedia.org/wiki/Impuls_%28Physik%29
3.6. Schlusserklärung
Ich erkläre hiermit, dass ich die Facharbeit ohne fremde Hilfe angefertigt und nur die im
Literaturverzeichnis angeführten Quellen und Hilfsmittel benützt habe.
Bad Neustadt a. d. Saale, den 26.1.2007
.....................................
(Unterschrift)