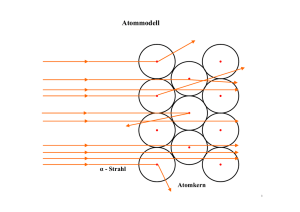
8 Das Bohrsche Atommodell 8. Das Bohrsche
Werbung

8 Das Bohrsche Atommodell 1. Einführung 1.1. Quantenmechanik – versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle: das Rutherfordexperiment 5. Das Photon: Welle und Teilchen 6. Teilchen als Welle (de Broglie) 7. Heisenbergsche Unschärferelation 8. Das Bohrsche Atommodell 8.1. Experimenteller Befund 1: Diskrete Spektren 8.2. Experimenteller Befund 2: Franck Hertz Versuch 8.3. Model: Die Bohrschen Postulate 8.4. Veranschaulichung des Models 1: Rydbergatome 8.5. Korrektur durch endliche Kernmasse 8.6. Veranschaulichung des Models 2: Myonische Atome 8.7. Veranschaulichung des Models 3: Positronium, Antiwasserstoff 8.8. Weitere Korrektur: Sommerfeld 8.9. Bohrmodell und DeBroglie Wellen 8.10. Die Grenzen des Bohrmodells 8 Das Bohrsche Atommodell 8.1. Der Experimentelle Befund 1: Diskrete Spektren Mit 2 Typen der Spektroskopie beobachtet man diskrete Energien im Wasserstoff Atom Schwarzer Strahler 8 Das Bohrsche Atommodell 8.1. Der Experimentelle Befund: Diskrete Spektren Mit 2 Typen der Spektroskopie beobachtet man diskrete Energien im Wasserstoff Atom a) Absorbtionsspektren Schwarzer Strahler Wasserstoff Gas Wasserstoff Absorbtionsspektrum 8 Das Bohrsche Atommodell 8.1. Der Experimentelle Befund: Diskrete Spektren Mit 2 Typen der Spektroskopie beobachtet man diskrete Energien im Wasserstoff Atom a) Absorbtionsspektren b) Emissionsspektren Helium Wasserstoff Emissionsspektrum Wellenlänge nm 8 Das Bohrsche Atommodell H Spektralanalyse Kirchhoff und Bunsen: Jedes Element hat charakteristische Emissionsbanden 8 Das Bohrsche Atommodell 8.1. Experimenteller Befund 1: Diskrete Spektren 8.2. Experimenteller Befund 2: Franck Hertz Versuch Potential 2 unelastische Stösse 1 unelastischer Stoss elastische Stösse C Strom A-B Quecksilber Dampf niedriger Druck Heizdraht (e- Quelle) Beschleunigungsspannung C-A Anregungsenergie von Quecksilber 4.9 eV Rydbergkonstante 109678 cm-1 infrarot sichtbar ganze Zahlen ultaviolett Lyman n1=1 Balmer n1=2 Paschen n1=3 8 Das Bohrsche Atommodell 8.1. Experimenteller Befund 1: Diskrete Spektren 8.3. Experimenteller Befund 2: Franck Hertz Versuch 8.3. Die Bohrschen Postulate Ein Atommodell analog zum Planetensystem (Rutherford) hat mehrere Probleme: 1) es erklärt keine Diskreten Energien 2) Es kann die Stabilität des Atoms nicht erklären, da ein kreisendes Elektron Energie abstrahlt Gleichgewicht zwischen Anziehung und Zentrifugalkraft: Coulomb Anziehung Z=1, e- Zentrifugalkraft: merω2 8 Das Bohrsche Atommodell Die Gesamtenergie des Elektron: E = Ekin + Epot 0 Energy Epot r negativ Energie die frei wird wenn Elektron von unendlich zum Radius r gebracht wird. 8 Das Bohrsche Atommodell Die Gesamtenergie des Elektron: E = Ekin + Epot Widerspruch zur klassichen Mechanik & Maxwellgleichungen: •Bewegte Ladung strahlt Energie ab, Elektron stürzt in Kern! •Strahlung ist nicht quantisiert keine diskreten Linien! 8 Das Bohrsche Atommodell Bohrsche Postulate (Niels Bohr 1913) •Elektronen bewegen sich auf Kreisbahnen •Die Bewegung ist strahlungsfrei n rn •Der Drehimpuls der Bahnen ist quantisiert l=n ħ (Historisch nicht korrekt) Ry = Rydbergkonstante (Ionisierungsenergie n=1) 109678 cm-1 8 Das Bohrsche Atommodell Einige Zahlenwerte: Radius des Wasserstoffatoms rn=1= 0.529 10-10m Ionisierungsenergie des Wasserstoffatoms En=1= 13.59 eV Z2 !! dh. Uran 115 keV Heisenbergsche Unschärfe ∆x ∆px ≥ ħ 8 Das Bohrsche Atommodell 8.4. Veranschaulichung des Models 1: Rydbergatome n=10 000 Radius = 0.6 mm En=10 000= 1.3 10-7 eV 0.01 mm wurde wirklich erreicht! Rydberg Atome Heisenbergsche Unschärfe ∆x ∆px ≥ ħ •rn ∝ n2 n!1 •vn ∝ 1/n Übergang zu klassischer Bahn (Bohrsches Korrespondezprinzip) 8 Das Bohrsche Atommodell 8.4. Veranschaulichung des Models 1: Rydbergatome 8 Das Bohrsche Atommodell 8.4. Veranschaulichung des Models 1: Rydbergatome Heisenbergsche Unschärfe ∆x ∆px ≥ ħ n!1 Übergang zu klassischer Bahn (Bohrsches Korrespondezprinzip) Lebensdauer steigt E3 8 Das Bohrsche Atommodell 8.5. Korrektur durch endliche Kernmasse mproton / melektron = 1836 Korrektur: gemeinsame Bewegung um Massenschwerpunkt Wasserstoff Energie 0.0545 % 10-15m -5 des Atoms! Kerndurchmesser 10 -10m 10 Wasserstoff 3 Isotope: Massenschwerpunkt liegt nicht im Kern H 1 Proton + 1 Elektron D (Deuterium) 1 Proton + 1 Neutron + 1 Elektron T (Tritium)(12.3 y) 1 Proton + 2 Neutronen + 1 Elektron 8 Das Bohrsche Atommodell 8.5. Korrektur durch endliche Kernmasse Folge: Isotope haben verschiedenen Spektrallinien Korrektur: Wasserstoff Energie 0.0545 % mdeuteron / mproton = 2 8 Das Bohrsche Atommodell 8.6. Veranschaulichung des Models 2: Myonische Atome 8.7. Veranschaulichung des Models 3: Positronium, Antiwasserstoff Elektronenmasse! Μyon mµ = 207 me 8 Das Bohrsche Atommodell Erzeugung von Μyonen an Protonenbeschleunigern: Pion (Masse 273 me) p + n -> p + p + π2.5 10-8s µ- + νµ Myon + Myonneutrino 2.2 10-6 s e- + νe + νµ Spektrum 207 fach höhere Energie 8 Das Bohrsche Atommodell 8.6. Veranschaulichung des Models 2: Myonische Atome Anwendung Myonischer Atome zur Messung der Struktur der Atomkerne (Ladungsverteilung, Deformations) Myonen-Bahnen sind teilweise im Kern -> Energie gibt Information über Ladungsverteilung des Kerns 8 Das Bohrsche Atommodell 8.6. Veranschaulichung des Models 2: Myonische Atome 8.7. Veranschaulichung des Models 3: Positronium, Antiwasserstoff Elektron Q=-1.6 10-19 C m=9.1 10-31kg=511keV/c2 E=mc2 Positron =Antiteilchen zum Elektron Q=+1.6 10-19 C m=9.1 10-31kg=511keV/c2 8 Das Bohrsche Atommodell 8.6. Veranschaulichung des Models 2: Myonische Atome 8.7. Veranschaulichung des Models 3: Positronium, Antiwasserstoff 1. Energieerhaltung: Gesamt 2*511keV 2. Impulserhaltung: z.B. 2 Photonen entgegengesetzt 2 Photonen 511 keV Positronium: e+ e- En=1=6.8eV Wasserstoff: p+ e- En=1=13,6eV rn=1=1,06 10-10m rn=1=0,53 10-10m 8 Das Bohrsche Atommodell 8.6. Veranschaulichung des Models 2: Myonische Atome 8.7. Veranschaulichung des Models 3: Positronium, Antiwasserstoff Para Positronium (entgegengesetzer Spin) T=1,25 10-10s Ortho Positronium (gleicher Spin) T=1,4 10-7s WARUM? Zerfällt in 3 oder mehr Photonen (Drehimpulserhaltung) 8 Das Bohrsche Atommodell 8.6. Veranschaulichung des Models 2: Myonische Atome 8.7. Veranschaulichung des Models 3: Positronium, Antiwasserstoff Positronium: e+ e- En=1=6.8eV Wasserstoff: p+ e- En=1=13,6eV Antiwasserstoff: p- e+ Antimaterie: 1995 CERN 1997 Fermilab rn=1=1,06 10-10m rn=1=0,53 10-10m En=1=13,6eV rn=1=0,53 10-10m 9 (!!!) Atome im Flug erzeugt 2002: ATHENA (CERN) 50 000 KALTE Antiwasserstoffatome in Falle http://livefromcern.web.cern.ch/livefromcern/antimatter/factory/AM-factory00.html 8 Das Bohrsche Atommodell 8.7. Veranschaulichung des Models 3: Positronium, Antiwasserstoff Positronium: e+ e- En=1=6.8eV Wasserstoff: p+ e- En=1=13,6eV Antiwasserstoff: p- e+ Fragen: Antimaterie: 1995 CERN 1997 Fermilab rn=1=1,06 10-10m rn=1=0,53 10-10m En=1=13,6eV rn=1=0,53 10-10m 9 (!!!) Atome im Flug erzeugt •Sind2002: die Spektrallinien ATHENA (CERN) exakt gleich? 50 000 KALTE Antiwasserstoffatome in Falle • Ist die Gravitation für Materie und Antimaterie gleich? http://livefromcern.web.cern.ch/livefromcern/antimatter/factory/AM-factory00.html 8 Das Bohrsche Atommodell 8.8. Weitere Korrektur: Sommerfeld Hα ist aufgespalten 8 Das Bohrsche Atommodell Keplerellipsen statt Kreisbahnen histo Nebenquantenzahl k (zu n) beschreibt rkleine g n u ä l k r E e Halbachse h c s ri h c o n t m m o k ) n iBewegung in Kernnähe p relativistische S r e b ü ( g n u r ä l k r E e -> E hängt auch von Elliptizität ab n r e d o M Sommerfeldsche Feinstukturkonstante α Geschwindigkeit auf n=1 Bahn = 1/137 c 8 Das Bohrsche Atommodell 8.8. Weitere Korrektur: Sommerfeld Es gibt eine weitere Aufspaltung, Eine weitere Quantenzahl zusätzlich zu n Hα ist aufgespalten 8 Das Bohrsche Atommodell 8.9. Bohrmodell und DeBroglie Wellen Bohr postulierte n diskret, Drehimpuls ganzzahlig, Kreisbahnen daraus folgt in der klassischen Mechanik ein quantisierter Radius rn Dieser Radius passt zur deBroglie Wellenlänge eines Elektrons mit der jeweiligen Bohrschen Energie: De Broglie Wellenlänge: λ = h/p = h/ √2m0Ekin 8 Das Bohrsche Atommodell 8.10. Die Grenzen des Bohr Modells Das Bohrmodell lässt viele Fragen offen: Wie intensiv sind die Linien? Wie lange lebt der n=2 ??? Wieso zefällt es? Mehrelektronen: Helium 1. Spektrum Erklären 2. Warum zerfällt es nicht? 8 Das Bohrsche Atommodell 8.10. Die Grenzen des Bohr Modells Das Bohrmodell lässt viele Fragen offen: Ein klassisches 2 Elektronenatom wäre nicht stabil Elektron 1 Elektron 2 Farbumschaltung wenn R-e-e klein 8 Das Bohrsche Atommodell 8.10. Die Grenzen des Bohr Modells Das Bohrmodell lässt viele Fragen offen: Wie intensiv sind die Linien? Wie lange lebt der n=2 ??? Wieso zefällt es? Mehrelektronen: Helium 1. Spektrum Erklären 2. Warum zerfällt es nicht? Bohr “The Dilemma of the Helium Atom” J.H. Van Fleck Phil. Mag. 44 (1922)842 Langmiur Lande