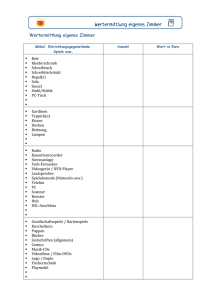
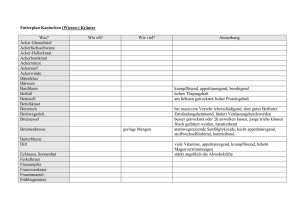
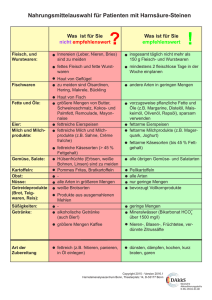
Definition - Satz

Definition — Satz — Beweis
Stephan Lukits
([email protected])
5. September 2013
Zusammenfassung
Eine kompakte Gebrauchsanleitung für die mathematische Vorgehensweise. Es wurde der Spagat versucht auf
so wenig Seiten wie möglich so umfassend und präzise
wie nötig das grundlegende Erkenntnisprinzip der Mathematik darzulegen.
INHALTSVERZEICHNIS
2
Inhaltsverzeichnis
Definition—Satz—Beweis
3
Begriffsbildung
4
Definition . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
Logik
10
Prädikatenlogik
12
Syntax . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
Semantik . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
Satz — Beweis . . . . . . . . . . . . . . . . . . . . . . . .
19
Schluß- und Äquivalenzregeln . . . . . . . . . . . . . .
20
Schlussregeln . . . . . . . . . . . . . . . . . . . . .
21
Äquivalenzregeln . . . . . . . . . . . . . . . . . . .
23
Beispiel
25
Literatur
31
Definition—Satz—Beweis
3
Definition—Satz—Beweis
Definition — Satz — Beweis. Dies ist im Groben das Muster
nach dem mathematische Inhalte dargestellt werden. Wenn
man Glück hat, findet man vor der Definition noch eine Motivation oder ein Beispiel. Das wesentliche aber ist dieses Triumvirat. Im Rahmen der Definition charakterisiert man die
Gegenstände, über die man spreche möchte, indem man deren charakterisierenden Eigenschaften aufzählt. Dabei geht
man in der Regel zunächst von einer Reihe Fakten aus, die
schlicht als wahr vorausgesetzt werden. D.h. man charakterisiert Gegenstände indem man bestimmte Aussagen über
diese formuliert und geht ohne Beweis davon aus, dass Gegenstände existieren, über die das gesagte ausgesagt werden
kann. Diese grundlegenden Aussagen nennt man Axiome.
Das mindeste, was man von Axiomen fordert, ist ihre Widerspruchsfreiheit. Nachdem der Untersuchungsgegenstand
— dessen Motivation ohne weiteres außerhalb der Mathematik liegen kann — definiert ist, wird begonnen diesen zu
untersuchen, indem man die axiomatischen Aussagen miteinander logisch verknüpft und dadurch weitere Aussagen
über den Untersuchungsgegenstand erhält. Durch die logische Verknüpfung wird — stets nur unter der Voraussetzung,
dass die Axiome wahr sind im Sinne von widerspruchsfrei —
ein Beweis für die neuen Eigenschaften geliefert. Das diese logischen Verknüpfungen als Beweis anerkannt werden,
liegt daran, dass sie wahrheitskonservierend sind. D.h. die
(Denk)Regeln, mit denen wir weitere Aussagen erhalten, sind
so gewählt, dass aus wahren Aussagen stets wieder wahre
Aussagen folgen. Die auf diese Weise gefundenen wahren
Aussagen, können nun dazu dienen weitere Begriffe zu defi-
Begriffsbildung
4
nieren und das Prozedere beginnt von neuem. Im Folgenden
werden die einzelnen Aspekte dieser Methode etwas detaillierter dargestellt.
Begriffsbildung
Ein Begriff ist etwas, das sich über einen Gegenstand aussagen lässt. Dabei verstehen wir unter einer Aussage im weiteren einen Aussagesatz in deutscher Sprache, der objektiv
entweder wahr oder falsch ist. Eine Aussage ist genau dann
objektiv wahr, wenn jeder, der über die selben Voraussetzungen verfügt, unter denen die Aussage getroffen wurde, dieser auch den Wahrheitswert wahr zuordnet. Alle Gegenstände über die etwas ausgesagt werden soll, werden im (Diskurs)Universum zusammengefasst. Begriffe können im Subjekt und im Prädikat eines Satzes zu finden sein, sie können
Substantiv, Verb oder Adjektiv sein. Z.B. „Maler streichen ein
Haus weiß“ mit dem Subjekt „Maler“ einem Objekt „Haus“
und dem Prädikat „streichen ein Haus weiß“. Offenbar können wir über einen Gegenstand aussagen, dass er ein Maler,
ein Haus oder weiß ist und, dass er streicht. Also finden
wir in diesem einfachen Satz schon vier Begriffe. Einen im
Subjekt und drei im Prädikat. Zwei sind ein Substantiv, einer ein Verb und einer ein Adjektiv. Keine Begriffe sind z.B.
Bindewörter, Artikel, Eigenname oder Subjekte mit Demonstrativpronomen bzw bestimmten Artikeln, die auf einen gegenstand hinweisen oder einen Eigennamen ersetzen wie z.B.
„dieses Haus“ oder „die Sonne“.
Die ersten Begriffe erlernen wir mit unserer Sprache durch
Begriff
Aussage
Universum
Begriffsbildung
5
„Zeige-Handlungen“ auf Beispielen und Gegenbeispielen für
den zu erlernenden Begriff. So bekommen wir beispielsweise
so lange Pferde und nicht-Pferde gezeigt, bis wir einen entsprechenden Gegenstand als solches identifizieren können.
Diese Begriffsbildung durch Beispiel ist zwar in der Mathematik unüblich, kommt aber vor. Mir scheint diese Vorgehensweise gerade bei Darstellungen verbreitet, die sich den
Anstrich geben wollen besonders „einfach“ zu sein. Diese Anschaulichkeit erkauft man sich allerdings durch ein schwerwiegendes Problem. Über ein Beispiel kann man nicht argumentieren bzw nur über die Beispiele, die man hat, etwas
aussagen. So ist auch das oben geschilderte Erlernen des Begriffs Pferd immer an unsere bisherige Erfahrung (= gesehene Beispiele und Gegenbeispiele) gekoppelt. Wir können
schon seit Jahren korrekt Pferde erkennen, bis wir erstmals
einen Maulesel sehen und plötzlich nach all den Jahren wieder vor der Frage stehen, ist das nun ein Pferd oder nicht.
Wüssten wir dagegen charakterisierende Eigenschaften eines
Pferdes, die wir überprüfen können, dann sollte es auch kein
Problem mehr sein, den Maulesel als nicht-Pferd zu erkennen.
In der Mathematik kommt noch erschwerend hinzu, dass eine mathematische Erkenntnis immer über eine unendliche
Menge mathematischer Gegenstände gewonnen wird. Weshalb Beispiele — wenngleich für die Vorstellung von einem
Begriff unverzichtbar — nicht ausreichen für die Bildung eines Begriffs.
Mit dieser Schwierigkeit hören aber die Probleme der Begriffsbildung durch Beispiel nicht auf. Ein weiteres Problem
ist, dass derjenige, der auf das Pferd zeigt am selben Ort sein
muss wie derjenige, dem das Pferd gezeigt wird. So wird dieses Vorgehen immer schwieriger je spezieller der zu vermit-
Definition
6
telnde Begriff wird, d.h. je weniger um die zu vermittelnden
Bedeutung des Begriffs wissen. Um dem Abhilfe zu verschaffen, führt man Begriffe ein, indem man sie definiert. D.h.
man zählt alle charakterisierenden Eigenschaften von Gegenständen auf, die unter den Begriff fallen sollen. Dabei geht
man natürlich davon aus, dass ein gewisser Vorrat an Begriffen schon vorhanden ist, der mit dem Erlernen der Sprache
erworben wurde. Zum Beispiel ließe sich der Mensch als ungefiederter Zweibeiner definieren. Nun mag es den Anschein
haben, dass Menschen, Krone der Schöpfung, viel mehr sind
als ungefiederte Zweibeiner. Allerdings ist eine zentrale Aufgabe der Begriffsdefinition, dass sie uns dabei helfen soll, bestimmte Gegenstände von allen anderen zu unterscheiden.
Und dafür reicht es in der Tat aus ungefiedert zu sein und auf
zwei Beinen zu gehen, um zweifelsfrei als Mensch identifizierbar zu sein. Definition kommt vom lateinischen Definitio =
Abgrenzung, welches sich zusammensetzt aus de = ab/weg
und finis = Grenze. Interessieren uns allerdings andere Eigenschaften des Menschen, dann wäre es natürlich für unsere Mensch-Theorie nicht sinnvoll Menschen als ungefiederte Zweibeiner zu definieren. Gegenstände, die sich ob ihrer
Gleichartigkeit zusammenfassen lassen, können mehr als nur
einen Satz charakterisierende Eigenschaften haben. Z.B. ist
auch der Quotient von Hirnmasse und Körpergewicht ein Alleinstellungsmerkmal des Durchschnittsmenschen, oder nach
dem Buddhismus ist die „Erkenntnisfähigkeit des Wesens der
Dinge“ eine Eigenschaft, die außer den Menschen niemand
hat.
Definition Eine Begriffsdefinition ordnet einem Wort
B dem sogenannten Definiendum äquivalent eine Reihe von
Begriffsdefinition
Definiendum
Definition
7
schon bekannten Begriffen B1 , . . . , Bn das sog. Definiens zu.
Das Wort B steht dann für einen neuen Begriff. Eingangs
wurde bemerkt, dass ein Begriff etwas ist, das sich von einem
Gegenstand aussagen lässt. Also bedeutet das „äquivalent“
in diesem Zusammenhang: Jeder Gegenstand von dem ich
B1 , . . . , Bn aussagen kann, von dem kann ich auch B aussagen; Jeder Gegenstand von dem ich B aussagen kann, von
dem kann ich auch B1 , . . . , Bn aussagen. Wir definieren z.B.
Mensch(x) :⇔ ungefiedert(x) und zweibeinig(x)
Wobei x für einen Gegenstand unseres Universums steht und
:⇔ die, durch Definition bestehende, Äquivalenzbeziehung
ausdrückt. In Prosa übersetzt also
Ein Gegenstand heißt genau dann Mensch, wenn er ungefiedert und zweibeinig ist.
Wenn diese Definition tatsächlich charakterisierend ist, dann
hat alles, von dem wir aussagen würden, dass es ein Mensch
ist, kein Federkleid und zwei Beine. Außerdem könnten wir
von allem, das keine Federn hat und zweibeinig ist, aussagen, dass es ein Mensch ist. Durch diese äquivalente Charakterisierung vereinbaren wir aber auch, dass alles, was kein
Mensch ist, gefiedert ist oder keine zwei Beine hat. Und Umgekehrt, dass alles, was gefiedert oder nicht zweibeinig ist,
kein Mensch ist.
Noch drei kleine Anmerkungen. In der modernen Mathematik ist es üblich, dass man positiv definiert, also nicht durch
die Abwesenheit einer Eigenschaft wie z.B. ungefiedert. Bei
Euklid findet man z.B. noch: „Ein Punkt ist das, was keine
Teile hat“. Während „undgefiedert sein“ noch in Ordnung
Definiens
Definition
8
ist, weil dies eine unmittelbar sinnlich wahrnehmbare Eigenschaft ist, wird es im Allgemeinen problematisch. Denn damit ein Gegenstand im Allgemeinen eine nicht unmittelbar
wahrnehmbare Eigenschaft zweifelsfrei nicht hat, benötige
wir eine Liste aller Eigenschaften, die dieser Gegenstand hat,
um quasi nachzuschlagen, ob diese Eigenschaft dabei ist oder
nicht. Dies ist erkenntnistheoretisch schon allein deshalb problematisch ist, weil wir von keinem Gegenstand eine solche
Liste besitzen.
Des weiteren fordert man in der Mathematik, dass das Definiendum nicht im Definiens vorkommt. Während diese Forderung in der Umgangssprache zum Scheitern verurteilt ist,
klappt es in der Mathematik bzw. im Rahmen einer Theorie
ganz gut. Um der Problematik gewahr zu werden, nehmen
Sie sich einfach ein Konversationslexikon zur Hand, schlagen
es irgendwo auf und nehmen den ersten Begriff der Ihnen
begegnet. Dann lesen Sie die Erklärung dieses Begriffes und
schlagen jeden Begriff in dieser Erklärung nach, dann jeden
Begriff in der Erklärung eines Begriffs aus der Erklärung des
ursprünglichen Begriffs und so weiter. Es sollte nicht allzulange dauern, bis Sie eine Begriffserklärung finden, in der Ihr
ursprünglicher Begriff steht. Da wir Begriffe durch ihr Definiens ersetzen können, wäre das Definiendum im Definiens
zu finden. Da sich die klassische Mathematik auf die Mengenlehre zurückführen lässt und es in dieser nur genau einen
undefinierten Begriff „ist Element von“ gibt, der nicht erklärt
wird, haben wir hier diese Problematik nicht.
Schließlich formuliert man eine Definition in der Regel wie
folgt
x heißt genau dann B , wenn x B1 , . . . , Bn ist.
Definition
9
An Stelle von „heißt“ schreiben wir auch „nennt man“ und
an Stelle von „genau dann“ formuliert man auch „dann und
nur dann“. Manchmal findet man anstelle von „heißt“ auch
eine Form von Sein, also etwa „ x ist genau dann B , wenn. . . “.
Meines Erachtens ist das schlechter Stil, weil dadurch der Eindruckt erweckt werden könnte, dass durch die Definition etwas ins Seien tritt, also eine Definition ein schöpferischer Akt
ist. Dies ist aber nicht der Fall. Dadurch das ich einen Begriff
definiere, existieren keine Gegenstände, die unter den Begriff
fallen, d.h. Gegenstände über die sich das Definiens aussagen
lässt. Im Gegenteil wird vor oder nach jeder Definition ein
Existenzsatz erwartet, in dessen Beweis die Existenz solcher
Gegenstände gezeigt wird. Außerdem fällt oftmals das „genau dann“ unter den Tisch. In Kombination mit einer Form
von sein, wie z.B. hier
. . . , die Würfe sind unabhängig, falls p(w, w 0 ) = p(w)p(w 0 ) für alle
(w, w 0 ) ∈ Ω2 ist.
([Aig06, S. 19])
könnte nun leicht der Eindruck entstehen, dass das unabhängig sein von „Würfen“ (was auch immer das ist) aus dem Umstand p(w, w 0 ) = p(w)p(w 0 ) gefolgert werden könnte, aber
nicht umgekehrt. Tatsächlich soll hier aber der Begriff unabhängig definiert werden. In solchen Fällen müssen wir
genau auf den Kontext achten, ob im Weiteren der genannten Begriff ebenfalls hinreichend ist, um auf die genannten
hinreichenden Voraussetzungen zu schließen, d.h. im obigen
Beispiel, dass wir darauf achten müssen, ob aus „die Würfe
sind unabhängig“ der Sachverhalt „ p(w, w 0 ) = p(w)p(w 0 )“ im
Weiteren gefolgert wird.
Logik
10
Logik
Die wissenschaft der „Logik“ untersucht die Regeln nach denen wir allein Kraft unseres Denkens von vorhanden Tatsachen weitere Tatsachen folgern können. Es gibt verschiedene Arten des Schließens. Nach Peirce in [Pei02, S. 171 ff]:
Deduktives Schließen, induktives Schließen und apduktives
Schließen. Letzteres findet sich häufig in der Diagnostik. Wir
finden eine Situation vor und versuchen „Rückschlüsse“ auf
deren Ursachen zu ziehen. Beim induktiven Schließen, schließen wir aus einer Beobachtung, dass unter den selben Voraussetzungen immer wieder das selbe beobachtet werden kann.
Typisches Beispiel ist hier der Physikunterricht. Man lässt beispielsweise an einem Punkt der Erde zu einem bestimmten
Zeitpunkt eine Kugel fallen und erhält über Messungen die
Fallbeschleunigung, also die Erdanziehungskraft und glaubt
dann, dass zu allen anderen Zeitpunkten in allen anderen Orten der Welt die selbe Erdanziehung herrscht. Oder wenn
man auf eine heiße Herdplatte fasst; auch hier wird man
induktiv schließen, dass ein weiteres fassen auf eine heiße
Herdplatte wieder zu einer Verbrennung führt. Das deduktive Schließen wird auch ableitendes Schließen genannt. Hier
schließt man von (wahren) Prämissen ausgehend wahrheitserhaltend auf weitere wahre Aussagen. Z.B. sagt A zu B ,
dass A bei schönen Wetter am Nachmittag ins Freibad zum
Schwimmen geht. Später am Tag trifft B auf C und C fragt,
ob B denn wisse wo A ist. Nun ist es Nachmittag und die
Sonne scheint, also wird B , obwohl B nicht (physisch) feststellen kann wo A ist, ohne zu zögern antworten: A ist im
Freibad. Dabei hat B einen sogenannten wahrheitserhaltenden Schluss gezogen:
Logik
11
Wenn es wahr ist, dass A bei Sonnenschein und Nachmittagsstunde im Freibad ist, und wenn es wahr ist, dass die
Sonne scheint und es am Nachmittag ist, dann ist auch
wahr, dass A im Freibad ist.
A könnte natürlich auch gelogen haben, dennoch bleibt der
logische Schluss korrekt auch wenn A nicht im Freibad zu finden ist. In diesem Falle ist schlicht die Voraussetzung „wenn
nachmittags die Sonne scheint, ist A im Freibad“, die beim
Ziehen des Schlusses als wahr angenommen wurde, nicht erfüllt. Für diesen Fall wurde aber gar keine Aussage gemacht,
also insbesondere auch keine falsche.
Induktives und apduktives Schließen sind unsichere Schlussweißen. Dies liegt daran, dass wir im ersteren Fall sicher sein
müssen, dass wir alles wesentliche für unseren Schluss auch
tatsächlich beobachtet haben. Z.B. könnte der erste Radfahrer, den ein Kind sieht, blondhaarig sein. Daraus könnte das
Kind nun induktiv folgern, dass alle Radfahrer blondhaarig
sind. Dieses Beispiel erscheint vermutlich nur deshalb so absurd, weil wir schon so viele Radfahrer anderer Haarfarbe
gesehen haben. Beim apduktiven Schließen müssen wir sicher sein, dass wir alle Voraussetzungen die zur vorgefundenen Kombination von Symptomen führt auch tatsächlich
kennen. Die Unsicherheit dieser beiden Schlussweisen liegt
eben darin sicherzustellen alles wesentliche beobachtet bzw
alle möglichen Voraussetzung zu kennen, was ziemlich unwahrscheinlich ist, da wir im Allgemeinen unvollständig informiert sind. In der deduktiven Logik werden nur sichere
Schlüsse von Wahrem zu Wahrem gezogen. Denn in einem
deduktiven Schluss sind alle Voraussetzung enthalten, unter
denen der Schluss wahrheitserhaltend ist. Vielleicht könn-
Prädikatenlogik
12
te man auch sagen, dass das deduktive Schließen, das einzige Schließen ist, bei dem man bezüglich des zu ziehenden
Schlusses vollständig informiert ist.
Prädikatenlogik
Ein entweder objektiv wahrer oder objektiv falscher Aussagesatz mit unbestimmten Satzgegenstand, heißt (einstellige)
Satzfunktion oder Prädikat; zum Beispiel: „ x ist die kleinste Primzahl“. Ein Platzhalter für einen konkrete Gegenstand,
wie x im vorstehenden Prädikat, wird im weiteren Variable
genannt (Begriffsbildung durch Beispiel!). Dieses Konzept
lässt sich verallgemeinern indem man neben dem Nominativ
weitere (grammatikalische) Objekte unbestimmt lässt. So erhält man mehrstellige Satzfunktionen wie z.B.
Prädikat
Variable
G(x, y) := “x ist größer als y“ oder K(x, y) := x ist die kleinste y,
die eine (unbestimmte) zweistelligen Beziehung ausdrücken
(Begriffsbildung durch Beispiel). Die Reihenfolge der Stellen in einer Beziehung sind signifikant. Allgemein wird die
erste Stelle der Nominativ sein, während die übrigen Stellen
die (grammatikalischen) Objekte sind. Konkrete Gegenstände werden im Weiteren in Abgrenzung zu Variablen Konstanten genannt. Sei P/n ein n-stelliges Prädikat und sei c eine
Konstante (des Universums). P/n heißt genau dann an der
i -ten Stelle instantiiert, wenn die i -te Variable durch c ersetzt
ist. Das Prädikat P/n heißt genau dann atomare Aussage,
wenn es an jeder Stelle instantiiert ist1 . Z.B. ist G(5, 3) =„5 ist
größer als 3.“ eine (wahre) Aussage oder K(Berlin, Stadt) =
„Berlin ist die kleinste Stadt“ eine (falsche) Aussage.
1
n Konstanten ersetzen entsprechend ihrer Reihenfolge die Variablen der
Satzfunktion
Beziehung
Konstante
instantiiert
13
Syntax
Eine weitere Möglichkeit von Prädikaten Aussagen zu gewinnen ist, die Variablen über den Gegenständen des Universums
zu quantifizieren. Wir sprechen dann auch von einem quantifizierten Prädikat und schreiben ∀x i P(. . . , x i , . . .) für eine allquantifizierte Variable in P und ∃x i P(. . . , x i , . . .) für eine existenzquantifizierte Variable in P . Dabei drückt die Allquantifizierung aus, dass wir an dieser Stelle über alle Gegenstände
des Universums etwas aussagen, während wir bei der Existenzaussage nur über mindestens einen gewissen Gegenstand
des Universums etwas aussagen. Nehmen wir exemplarisch
die Prädikate T (x) := „x ist ein Topf“, D(x) := „x ist ein Deckel“ und P(x, y) := „ x passt auf y “. Dann nehmen wir noch
an, dass wir uns im Universum der Töpfe und Deckel befinden
und können nun die Aussage formulieren
quantifizierten Prädikat
allquantifiziert
existenzquantifiziert
∀x : T (x) ⇒ ∃ y D( y) ∧ P( y, x)
In Prosa: Zu jedem Topf gibt es einen passenden Deckel. Im
Falle einer Allquantifizierung kann die quantifizierte Variable
also durch jeden Gegenstand des Universums ersetzt werden,
während bei der Existenzquantifizierung nur zugesichert wird,
dass es im Universum einen Gegenstand gibt, den wir einsetzen können, sodass die Aussage wahr ist. Wir können jetzt
den Begriff atomare Aussage verallgemeinern. Ein n-stelliges
Prädikat P/n heißt genau dann atomare Aussage, wenn jede
Stelle von P entweder instantiiert oder quantifiziert ist.
Syntax Nun können wir rekursiv die (zusammengesetzten) Aussage in voller Allgemeinheit und deren formale Syntax definieren.
• Jede atomare Aussage ist eine Aussage. Seien A1 und
atomare Aussage
Semantik
14
A2 Aussagen, dann ist
• „Es ist nicht der Fall, dass A1 “ — formal: ¬A1 ,
• „A1 und A2 “ — formal: A1 ∧ A2 ,
• „A1 oder A2 “ — formal: A1 ∨ A2 ,
• „Wenn A1 dann A2 “ — formal: A1 ⇒ A2 und
• „A1 ist genau dann der Falle, wenn A2 “ — formal: A1 ⇔
A2
je eine Aussage. Die erste logische Operation heißt Negation die zweite Konjunktion, die dritte Disjunktion, die vierte
materielle Implikation und die fünfte materielle Äquivalenz.
Die Aussagen einer Konjunktion heißen Konjunkt, die der Disjunktion Disjunkt. Die erste Aussage der materiellen Implikation heißt Antezedens und die zweite Konsequenz oder Sukzedens. Im Verlauf dieses Abschnittes werde ich abkürzend
auch nur von der Implikation bzw. Äquivalenz sprechen und
damit eine materielle Implikation bzw. Äquivalenz meinen.
Natürlich sind Aussagesätze nicht immer genau so aufgebaut,
dass ihre logische Struktur sofort offensichtlich ist. Z.B. „Die
Drei ist weder gerade noch ein vielfaches von 5“. Die logische
Struktur dieses Satzes ist „Es ist nicht der Fall, dass die Drei
gerade ist und es ist nicht der Fall, dass die Drei ein vielfaches
von 5 ist“. Ein Satz dessen logische Struktur nicht offensichtlich ist, muss also paraphrasiert werden damit diese zu Tage
tritt.
Semantik Beim logischen Argumentieren interessiert
uns nur der Wahrheitsgehalt von Aussagen, von jeglichem
Aussage
Negation, Konjunktion,
Disjunktion
Implikation, Äquivalenz
Konjunkt, Disjunkt
Antezendens,
Konsequenz, Sukzedens
Semantik
15
anderen Inhalt wird abstrahiert. Die Semantik einer Aussage
reduziert sich also auf Ihren Wahrheitsgehalt. Dies ist aber
auch notwendig, denn unsere „Denkregeln“ sollen ja nicht
nur für einen bestimmten Gegenstand unserer Überlegungen
geeignet sein, sondern sie sollen unabhängig von dem Gegenstand gültig sein, über den Nachgedacht wird. Für die Semantik (atomarer) Aussagen gilt grundsätzlich, dass wir jede
beliebige Aussage als wahr annehmen dürfen. Solche Aussagen heißen dann Prämissen. Die Schlüsse, die wir daraus
ziehen, sind natürlich nur unter der Voraussetzung von erkenntnistheoretischem Nutzen, wenn die als wahr angenommene Aussagen auch wahr sind. Aussagen die per Definition
wahr sind heißen Axiome. Die Semantik zusammengesetzter
Aussagen ist für beliebige Aussagen A1 und A2 wie folgt definiert.
• Eine Negation ¬A1 heißt genau dann wahr, wenn A1
falsch ist.
• Eine Konjunktion A1 ∧ A2 heißt genau dann wahr, wenn
beide Aussagen wahr sind.
• Eine Disjunktion A1 ∨ A2 heißt genau dann wahr, wenn
nicht beide Aussagen falsch sind.
• Eine Implikation A1 ⇒ A2 heißt genau dann wahr, wenn
nicht A1 wahr und A2 falsch ist.
• Eine Äquivalenz A1 ⇔ A2 heißt genau dann wahr, wenn
entweder beide Aussagen falsch sind, oder wenn beide
wahr sind.
• Eine Allquantifizierung ∀xA heißt genau dann wahr, wenn
Semantik
Prämisse
Axiom
Semantik
16
A für alle Instantiierungen von x durch Gegenstände
des Universums wahr ist.
• Eine Existenzquantifizierung ∃xA heißt genau dann wahr,
wenn es im Universum mindestens einen Gegenstand c
gibt, so dass A für c an der Stelle von x wahr ist.
An den Formulierungen der Semantikdefinitionen von Disjunktion, Implikation und Äquivalenz kann man vielleicht
schon erkennen, dass sich diese auf die ersten beiden zurückführen lassen. Während man die Allquantifizierung als fortgesetzte Konjunktion über den Gegenständen des Universums
interpretieren kann, lässt sich die Existenzquantifizierung als
fortgesetzte Disjunktion über den Gegenständen des Universums auffassen. Eine Motivation und Diskussion warum man
den Wahrheitsgehalt zusammengesetzter Aussagen gerade so
definiert ist z.B. in [Buc98] und [Tar66] zu finden.
Die durch die vorstehende Syntax und Semantik definierte
Logik heißt Prädikatenlogik 1. Stufe (ohne Identität) oder
kurz PL-1. Anstatt von Stufe spricht man auch von Ordnung.
Sie hießt Prädikatenlogik, weil in ihr die atomaren Aussagen
Prädikate sind und die Stufen ergeben sich aus dem Gegenstand der Quantifizierung. In der 1. Stufe wird über die
Gegenstände des Universums quantifiziert in der 2. Stufe
über die Eigenschaften der Gegenstände des Universums in
der 3. Stufe über die Eigenschaften der Eigenschaften der
Gegenstände des Universums und so weiter. Um die Identität
(Gleichheit) in einem logischen Sinne definieren zu können,
müsste man über die Eigenschaften der Gegenstände des Universums quantifizieren. Denn nach Leibniz heißen zwei Gegenstände G1 und G2 genau dann gleich, wenn G1 alle Eigenschaften hat, die G2 hat und wenn G2 alle Eigenschaften hat,
PL-1
Semantik
17
die auch G1 hat. Leider muss man bei einer höherstufigen
Prädikatenlogik eine wichtige Eigenschaft von PL-1 aufgeben.
Da man dies in der Mathematik vermutlich nach Möglichkeit
vermeiden möchte, beschränkt man sich meist auf die Prädikatenlogik 1. Stufe ohne Identität und das Universum der
Mengen. Die Identität muss dann für alle mathematischen
Gegenstände ausdrücklich definiert werden.
Eine zusammengesetzte Aussage heißt genau dann logisch
wahr oder Tautologie, wenn Sie so zusammengesetz ist, dass
sie unabhängig vom Wahrheitsgehalt ihrer atomaren Aussagen wahr ist. Sei A eine Aussage. Da A als Aussage nur entweder objektiv wahr oder objektiv falsch sein kann, ist entweder
A oder ¬A wahr, also ist A ∨ ¬A gemäß der vorstehenden Semantikdefinition der Disjunktion logisch wahr. Z.B. ist „Die
Erde ist rund oder sie ist nicht rund“ eine Tautologie. „Die
Erde ist rund oder eine Scheibe“ ist keine Tautologie, weil eine Erde, die nicht rund ist, nicht zwangsläufig eine Scheibe
sein muss. Sie könnte z.B. auch ein Würfel sein. Auch „Eine
Zahl ist positiv oder negativ“ ist keine Tautologie, sondern eine falsche Aussage, da eine Zahl auch die Null sein kann. Wir
formalisieren das logisch wahre mit >.
Eine zusammengesetzte Aussage heißt genau dann logisch
falsch, Kontradiktion oder Widerspruch, wenn sie unabhängig
von den Wahrheitswerten ihrer atomaren Teilaussagen falsch
ist. Ebenso wie wir gerade bemerkten, dass eine der beiden
Aussagen A und ¬A wahr sein muss, können wir feststellen,
dass eine von beiden falsch sein muss. Also ist die (zusammengesetzte) Aussage A ∧ ¬A stets falsch, da eine Konjunktion dann und nur dann wahr ist, wenn beide Konjunkte wahr
sind. Wir formalisieren das logisch falsche mit ⊥.
Tautologie
Kontradiktion
Widerspruch
Semantik
18
Eine zusammengesetzte Aussage A0 ist eine logische Implikation oder logische Folgerung aus einer anderen Zusammengesetzten Aussage A, wenn A0 immer dann wahr ist, wenn auch
A wahr ist. Wobei auch dieser Zusammenhang zwischen A
und A0 aus der logischen Struktur der Teilaussagen von A und
A0 erwächst und nicht aus deren Wahrheitsgehalt. Angenommen A1 und A2 seien Aussagen, dann folgt A1 ∨ A2 logisch aus
A1 . Denn immer wenn A1 wahr ist, ist gemäß der Semantik
der Disjunktion auch A1 ∨A2 wahr, also ist A1 ∨A2 immer dann
wahr wenn A1 wahr ist. Nun ist eine materielle Implikation
gemäß ihrer Semantik nur dann falsch, wenn der Antezedens
wahr und die Konsequenz falsch ist. Das kann aber bei der
Implikation von A1 ⇒ A1 ∨ A2 nicht passieren, da wir gerade
feststellten, dass A1 ∨ A2 immer dann wahr ist, wenn auch A1
wahr ist. Wir können also die logische Implikation auf die
materielle Implikation zurückführen und mit deren Hilfe charakterisieren. A0 folgt genau dann logisch aus A, wenn die
materielle Implikation von A und A0 eine Tautologie ist. Oder
umgekehrt, wenn ¬(A ⇒ A0 ) bzw A ∧ ¬A0 eine Kontradiktion
ist. Letzteres nennt man auch logisches folgern durch Widerspruch.
Da wir als wahr angenommene Aussagen A1 , . . . , An aufgrund
der Semantik der Konjunktion ohne weiteres zu einer einzigen wahren konjunktiv verknüpften Aussage zusammenfassen können und diese auch wieder in ihre Konjunkte zerlegbar ist, können wir die logische Folgerung auf beliebig viele
Aussagen in der Voraussetzung fortsetzen:
A1 , A2 , A3 , . . . |= A :⇔ wahr(A), falls wahr(A1 ), wahr(A2 ), . . .
Ist also A immer dann wahr, wenn es auch die Aussagen A1 ,
A2 , A3 , . . . sind, dann ist A eine logische Folgerung der Aussa-
logische Implikation
logische Folgerung
A |= A0 gdw A ⇒ A0 ≡ >
Satz — Beweis
19
gen A1 , A2 , A3 , . . .
Zwei zusammengesetze Aussagen A und A0 heißen genau dann
logisch äquivalent, wenn die eine genau dann wahr ist, wenn
es die andere ist und zwar unabhängig vom Wahrheitsgehalt der atomaren Aussagen, aus denen sich die Aussagen
zusammensetzen. Sie sind also genau dann logisch äquivalent, wenn A0 eine logische Folgerung aus A ist und wenn A
eine logische Folgerung aus A0 ist. Betrachten wir die beiden
Aussagen A := ¬A1 ∨ A2 , A0 := A1 ⇒ A2 .
logisch äquivalent
A ≡ A0 gdw A |= A0 , A0 |= A
Angenommen erstere währe wahr. Dann gibt es per Definition drei Fälle in denen sie wahr ist. (1) A1 ist falsch; (2) A2
ist wahr; (3) A1 ist falsch und A2 ist wahr. Die zweite Aussage war gemäß der Semantik der Implikation nur dann falsch
wenn A1 wahr und A2 falsch ist. Keiner der drei genannten
Fälle stimmt mit dieser Situation überein. Wenn also A wahr
ist, dann ist auch A0 wahr. Nun gibt es auch drei Fälle in denen A0 wahr ist und Sie werden feststellen, dass sich keiner
dieser Fälle mit der Situation deckt, dass A falsch ist. Wenn
also A0 wahr ist, dann ist auch A wahr. Eine der beiden Aussagen ist also genau dann wahr, wenn es die andere ist, also
sind sie logisch äquivalent und (¬A1 ∨ A2 ) ⇔ (A1 ⇒ A2 ) ist
eine Tautologie.
Satz — Beweis Eine (logische) Argumentation oder
Beweisführung ist nun eine Aneinanderreihung logischer Folgerungen ausgehend von Prämissen oder Axiomen. Seien A1 , . . . ,
An Axiome. Dann heißen alle Aussagen, die sich in PL-1 logisch aus diesen Axiomen folgern lassen, Theorie der Axiome
A1 , . . . , An . Eine Aussage heißt Satz oder Theorem einer Theorie, wenn er sich aus den Axiomen der Theorie logisch folgern
Argumentation
Beweisführung
Theorie
Satz
Theorem
Schluß- und Äquivalenzregeln
20
lässt. Sätze die ohne großen Aufwand unmittelbar aus Definitionen folgen, nennt man Korollar2 . Sätze die eher technischer Natur sind und als Hilfe für folgende Sätze dienen
nennt man (heutzutage) auch Lemma. Noch eine Bemerkung
zur Notation. Mit den formalen Bezeichnungen ≡ und |=
für die logische Äquivalenz bzw. Folgerung und ⇒ sowie ⇔
für die materielle Implikation bzw. Äquivalenz wurde eine
gängige Formalisierungen von PL-1 gewählt. Im Gegensatz
dazu ist es in der Mathematik üblich ⇒ und ⇔ für logische
Umformungen zu verwenden anstelle von ≡ und |=. Dieser
Unterschied fällt allerdings beim Argumentieren im mathematischen Alltagsgeschäft nicht in’s Gewicht.
Schluß- und Äquivalenzregeln Um nun Aussagen
logisch umformen zu können benötigen wir noch ein paar
allgemeine logische Folgerungen und logische Äquivalenzen.
Wir notieren die Schlussregeln wie üblich indem wir die Voraussetzungen auflisten und, durch den sogenannten Schlussstrich getrennt, den ziehbaren Schluss unter die Voraussetzungen schreiben. Z.B.
A
A ∨ A0
Wie oben bereits bemerkt handelt es sich bei dem Vorstehenden genau dann um einen logisch gültigen Schluss, wenn
A ⇒ A ∨ A0 eine Tautologie ist. Lesen kann man vorstehende Schlussregel als „Unter der Annahme, dass die Aussage A
wahr ist, ist auch die Aussage A∨A0 für jede weitere Aussage A0
2
Lat. Kränzchen, das der römische Gastgeber bei einer antiken Party seinen Gästen schenkte. In diesem Sinne ist der Korollar ein geschenkter Satz.
Korollar
Lemma
21
Schluß- und Äquivalenzregeln
wahr.“ Dies lässt sich übrigens meist leicht mit der Wahrheitstafelmethode überprüfen. Dabei belegt man die Teilaussagen
der zu prüfenden Aussage mit allen möglichen Kombinationen von Wahrheitswerten. Z.B.
A A0
0 0
0 1
1 0
1 1
A ∨ A0
0
1
1
1
A ⇒ (A ∨ A0 )
1
1
1
1
Dabei sind in den ersten beiden Spalten alle Wahrheitswertekombinationen aufgelistet und in den übrigen Spalten sind
die aus der Semantikdefinition resultierenden Wahrheitswerte bezüglich der jeweiligen Belegung eingetragen. (Die 0
steht für falsch während 1 für wahr steht.)
Schlussregeln Nach dem sogenannten Gentzen-Kalkül des
natürlichen Schließens.
A
A0
A, A0
A ∧ A0
A
A ∨ A0
A ⇒ A0
Und-Einführung (UE)
Oder-Einführung (OE)
Implikations-Einführung (IE)
Gelingt es also aus einer Aussage A die Aussage A0 zu folgern,
dann kann mit der Implikations-Einführung auf A ⇒ A0 geschlossen werden, denn dann ist A0 immer wahr, wenn es
auch A ist.
A(c)
∀xA(x)
A(c)
∃xA(x)
All-Einführung (AE)
Existenz-Einführung (EE)
A
⊥
¬A
Negations-Einführung (NE)
Reductio ad absurdum
22
Schluß- und Äquivalenzregeln
Die All-Einführung ist nur unter der Voraussetzung gestattet, dass sich keine von c abhängige Aussage in den Prämissen von A(c) befindet, bzw dass c in A nur Folge von AllInstantiierungen ist. Z.B. kann aus ∀xA0 (x) mit der All-Instantiierung A0 (c) gefolgert werden und aus ∀xA0 (x) ⇒ A(x)
kann mit All-Instantiierung und der Implikations-Beseitigung
A(c) gefolgert werden und aus A(c) ohne weiteres ∀xA(x), da
alle Prämissen allquantifiziert waren. Wäre allerdings anstelle von ∀xA0 (x) nur A0 (c) Prämisse gewesen, dann kann man
zwar ebenso A(c) folgern aber nicht mehr ∀xA(x).
A ∧ A0
A
A0
Und-Beseitigung (UB)
∀xA(x)
A(c)
All-Beseitigung (AB)
A1 ∨ A2 ,
A1 A2
,
A A
A
Oder-Beseitigung (OB)
∃xA(x),
A0
A(c)
A0
Existenz-Beseitigung (EB)
A
A ⇒ A0
A0
Implikations-Beseitigung (IB)
A
¬A
⊥
Negations-Beseitigung (NB)
⊥
A
A
A
ex falso quod libet
Annahmeeinführung (AE)
Als weiteres Beispiel für die Wahrheitstafelmethode wird die
Oder-Beseitigung bewiesen. Diese Regel ist genau dann einen
logische Folgerung, wenn folgende Aussage eine Tautologie
ist
((A1 ∨ A2 ) ∧ ((A1 ⇒ A) ∧ (A2 ⇒ A))) ⇒ A
23
Schluß- und Äquivalenzregeln
SP1
SP2
SP3
A1 A2 A A1 ∨ A2 A1 ⇒ A A2 ⇒ A (S P1 ∧ (S P2 ∧ S P3 )) ⇒ A
0 0 0
0
1
1
0
1
1
0 0 1
0
1
1
0
1
1
0 1 0
1
1
0
0
0
1
0 1 1
1
1
1
1
1
1
1
0
1
0
0
1
1 0 0
1 0 1
1
1
1
1
1
1
1 1 0
1
0
0
0
0
1
1 1 1
1
1
1
1
1
1
Äquivalenzregeln Jede der folgenden Äquivalenzen kann
natürlich auch als zwei logische Folgerungen, also als zwei
Schlussregeln interpretiert werden.
Idempotenz:
A∧ A ≡
A∨ A ≡
A
A
Kommutativität:
A ∧ A0
A ∨ A0
A0 ∧ A
A0 ∨ A
Assoziativität:
(A1 ∧ A2 ) ∧ A3
(A1 ∨ A2 ) ∨ A3
Absorption:
A ∧ (A ∨ A0 )
A ∨ (A ∧ A0 )
Distributivität:
A1 ∧ (A2 ∨ A3 )
A1 ∨ (A2 ∧ A3 )
Doppelnegation:
¬¬A ≡ A
DeMorgan:
¬(A ∧ A0 )
¬(A ∨ A0 )
≡
≡
≡
≡
≡
≡
≡
≡
A1 ∧ (A2 ∧ A3 )
A1 ∨ (A2 ∨ A3 )
A
A
≡
≡
(A1 ∧ A2 ) ∨ (A1 ∧ A3 )
(A1 ∨ A2 ) ∧ (A1 ∨ A3 )
¬A ∨ ¬A0
¬A ∧ ¬A0
24
Schluß- und Äquivalenzregeln
Tautologieregeln:
A ∨ A0
A ∧ A0
≡
≡
A
A0
≡
≡
A0
F ≡⊥
A
F ≡>
Kontradiktionregeln:
A ∨ A0
A ∧ A0
Kontraposition:
A ⇒ A0 ≡ ¬A0 ⇒ ¬A
Implikationsregel:
A ⇒ A0 ≡ ¬A ∨ A0
Äquivalenzregel:
A ⇔ A0 ≡ A ⇒ A0 ∧ A0 ⇒ A
Quantifikations-Negation:
¬∀xA ≡
¬∃xA ≡
∃x¬A
∀x¬A
Quantifikation:
(∀xA) ∧ A0
(∀xA) ∨ A0
(∃xA) ∧ A0
(∃xA) ∨ A0
≡
≡
≡
≡
Quantifikationsdistribution:
(∀xA) ∧ (∀xA0 )
(∃xA) ∨ (∃xA0 )
≡
≡
∀x(A ∧ A0 )
∃x(A ∨ A0 )
∀ y∀xA
∃ y∃xA
∀xA ≡ ∀ yA[x/ y]
y nicht in A
∃xA ≡ ∃ yA[x/ y]
Quantifikationskommutation:
gebundenes Umbenennen:
∀x(A ∧ A0 )
∀x(A ∨ A0 )
∃x(A ∧ A0 )
∃x(A ∨ A0 )
∀x∀ yA ≡
∃x∃ yA ≡
Ein letzter hier noch zu erwähnender Sachverhalt erlaubt die
Ersetzung äquivalenter Teilaussagen. Seien A1 und A2 zwei
Aussagen und A01 eine Teilaussage von A1 . Sind A01 und A2
logisch äquivalent, dann kann unter entsprechender (gebundener) Umbenennung von Variablen in A2 die Teilaussage A01
durch A2 ersetzt werden ohne die Semantik (d.h. den Wahrheitsgehalt) von A1 zu ändern. Sei z.B A := A1 ∧ (A2 ⇒ A3 ),
Ersetzung äquivalenter
Teilaussagen
25
Beispiel
dann
A1 ∧ (A2 ⇒ A3 ) ≡ A1 ∧ (¬A2 ∨ A3 ) =: A0
A0 ist also genau deshalb zu A logisch äquivalent, weil A2 ⇒ A3
und ¬A2 ∨ A3 logisch äquivalent sind.
Beispiel
Um dem vorstehenden noch etwas Substanz zu geben, wird
exemplarisch ein verschwindender Teil der Mengenlehre axiomatisch eingeführt. Wie der Name schon sagt sind in unserem Universum nur Mengen. Wenn wir also ein Aussage der
Form ∀xA(x) formulieren, dann sagen wir etwas über alle
Mengen aus. Wir haben genau einen undefinierten Begriff,
der die Beziehung „ist Element von“ zwischen zwei Mengen
ausdrückt. Wir könnten also das zweistellige Prädikat für diese Beziehung wie folgt definieren
∈ (x, y) := x ist Element von y
Durch „:=“ werden zwei Ausdrücke als gleich definiert. D.h.
Wir können die eine Zeichenfolge durch die andere ersetzen.
Es ist üblich eine Infixnotation zu verwenden und die Negation auf den Prädikatsnamen anzuwenden
x ∈ y :=∈ (x, y)
x 6∈ y := ¬ ∈ (x, y)
Auch wird um der Langeweile vorzubeugen nicht immer „ist
Element von“ gesagt. Wir sagen auch z.B. „ x ist in y enthalte“, „ x ist aus y “, „ y enthält x “. Gemeint ist dabei aber immer
x ∈ y . Unsere erste Definition lautet
26
Beispiel
Eine Menge heißt genau dann leer, wenn sie keine andere Menge enthält und wird mit ; oder {} bezeichnet
∀x : leer(x) :⇔ ∀ y : y 6∈ x.
Die Schreibweise „:⇔“ bedeutet „ist definitionsgemäß logisch
äquivalent.“ D.h. wir können also über eine Menge, die keine
andere Menge enthält sagen, dass sie leer ist, ebenso wie wir
über eine leere Menge sagen können, dass keine andere Menge existiert, die ihr Element ist. Üblicherweise reicht es nicht
einen (abstrakten) Begriff zu definieren, man muss auch sicher stellen, dass es einen Gegenstand gibt der unter diesen
Begriff fällt. Dies fordern wir nun axiomatisch in unserem
ersten Axiom
Eine leere Menge existiert.
Das ist noch nicht sehr spannend, also machen wir gleich mit
unserem zweiten Axiom weiter.
Zwei Mengen heißen genau dann gleich, wenn die eine Menge alle Elemente der Anderen enthält und wenn
letztere alle Elemente der ersteren enthält.
Hier springt zum einen die logische Struktur nicht ins Auge
zum anderen kann man von „die eine Menge“ und „die andere Menge“ noch sprechen solange es nur um zwei Mengen
geht, möchte man eine höherstellige Beziehung ausdrücken
wird es schnell unübersichtlich. Nach dem Motto „Name and
conquer3 “ könnte man diesen Satz leichter lesbar aufschrei3
Benenne und herrsche
27
Beispiel
ben indem so viele Gegenstände namentlich eingeführt werden, wie miteinander in Beziehung gesetzt werden sollen. In
diesem Falle wird eine Beziehung zwischen zwei Mengen ausgedrückt. Also ein neuer Versuch
Seien M und M 0 Mengen. M und M 0 heißen genau dann
gleich, wenn jedes Element von M 0 auch ein Element von
M ist, und jedes Element von M auch ein Element von
M 0 ist.
Oder etwas kürzer
Seien M und M 0 Mengen. M und M 0 heißen genau dann
gleich, wenn eine Menge m genau dann Element von M
ist, wenn m eines von M 0 ist.
Dies gilt nun natürlich nicht nur für die genannten Mengen
M und M 0 , denn mit „Seien M und M 0 Mengen“ ist gemeint
„Seien M und M 0 beliebige Mengen“ M und M 0 können also
jedes Paar von Mengen aus dem Universum bezeichnen, weshalb vorstehendes genauso eine Allausage ist, wie die folgende formale Definition dieses zweiten Axioms.
∀X , Y : X = Y :⇔ ∀x : x ∈ X ⇔ x ∈ Y
Für alle Mengen X und Y gilt: X und Y heißen genau dann
gleich, wenn für alle Menge x gilt: x ist genau dann eine
Element von X , wenn es auch eines von Y ist. Damit haben
wir ein neues zweistelliges Prädikat „=“ durch die ElementBeziehung und einer logischen Beziehung definiert. Oben
wurde bemerkt, dass wir uns im Rahmen der Prädikatenlogik
zweiten Axioms
28
Beispiel
erster Ordnung ohne Identität befinden. Deshalb müssen wir
uns die Gleichheit definieren. Wir könnten uns nun überlegen, ob diese Definition sinnvoll ist. Im allgemeinen versteht
man unter dem Konzept der Gleichheit zweier Gegenstände
G1 und G2 , dass jede Eigenschaft die G1 zugeschrieben werden kann, auch bei G2 zu finden ist und umgekehrt. Da wir
nichts weiter über eine Menge aussagen können, als dass eine weitere Menge ein Element von ihr ist oder nicht, folgt,
dass die Elementbeziehung das einzige Kriterium ist, anhand
dessen wir zwei Mengen unterscheiden können. Zwei Mengen sind also verschieden, wenn ich von einer der beiden
aussagen kann, dass sie eine weitere Menge enthält, die in
der anderen der beiden Mengen nicht enthalten ist
∀X , Y : X 6= Y ⇔ ∃x : (x ∈ X ∧ x 6∈ Y ) ∨ (x 6∈ X ∧ x ∈ Y ).
Denn dann kann offenbar über eine der beiden Mengen innerhalb der Mengenlehre etwas ausgesagt werden, was über die
Andere nicht ausgesagt werden kann. Als kleines Intermezzo wird nun gezeigt, dass die rechte Seite der gerade formal
notierte Äquivalenz logisch äquivalent ist zur Negation des
Definiens des zweiten Mengenaxioms
¬(∀x : x ∈ X ⇔ x ∈ Y ) ≡ ∃x : (x ∈ X ∧ x 6∈ Y )∨(x 6∈ X ∧ x ∈ Y )
Mit der Quantifikations-Negation folgt
¬(∀x : x ∈ X ⇔ x ∈ Y )
≡∃x : ¬(x ∈ X ⇔ x ∈ Y )
mit der Äquivalenzregel und der Ersetzung äquivalenter Teilaussagen (EäT) ergibt sich
≡∃x : ¬(x ∈ X ⇒ x ∈ Y ∧ x ∈ Y ⇒ x ∈ X )
29
Beispiel
woraus mit der Implikationsregel und EäT folgt
≡∃x : ¬((x 6∈ X ∨ x ∈ Y ) ∧ (x 6∈ Y ∨ x ∈ X ))
dann wenden wir neben EäT die DeMorgansche Äquivalenz
an
≡∃x : ¬(x 6∈ X ∨ x ∈ Y ) ∨ ¬(x 6∈ Y ∨ x ∈ X )
das selbe nocheinmal in Verbindung mit der Doppelnegation
≡∃x : (x ∈ X ∧ x 6∈ Y ) ∨ (x ∈ Y ∧ x 6∈ X )
unter Anwendung der Kommutativität der Konjunktion erhalten wir den gewünschten Ausdruck
≡∃x : (x ∈ X ∧ x 6∈ Y ) ∨ (x 6∈ X ∧ x ∈ Y )
was zu beweisen war.
Nun haben wir hoffentlich eingesehen, dass die hier definierte Gleichheit mit unserer intuitiven Vorstellung von Gleichheit übereinstimmt: Wir können zwei Mengen die im oben
definierten Sinne gleich sind innerhalb unserer Mengentheorie nicht unterscheiden, d.h. wir können über eine der beiden
Mengen nichts aussagen, was wir nicht auch über die andere
Menge aussagen könnten.
Kommen wir zu unserem ersten Satz. Bei der Begriffsdefinition der leeren Menge hob ich „eine“ hervor und meinte damit
den unbestimmten Artikel, nicht das Zahlwort. Ist das Zahlwort gemeint wird oft „genau eine“ geschrieben, um Missverständnissen vorzubeugen. In der ersten Begriffsdefinition und im ersten Axiom wurde also offen gelassen, ob es
30
Beispiel
im Universum der Mengen nur genau eine leere Menge oder
mehrere leere Mengen gibt. Mit unserem zweiten Axiom können wir die Antwort auf diese Frage als ersten Satz unserer
Mengentheorie beweisen. Bevor wir mit unserem prädikatenlogischen Formalismus zu Werke gehen, (wenn wir das
überhaupt wollen) können wir uns informell überlegen wie
diese Frage wohl entschieden wird. Nehmen wir einmal an,
wir hätten zwei leere Mengen ;1 und ;2 . Dann gilt für die
eine, dass keine der übrigen Mengen ein Element von ihr ist,
was für die andere per Definitionem der leeren Menge auch
gilt. Offenbar unterscheiden Sie sich bezüglich der Elementrelation nicht, also sind sie gleich, also ist die leere Menge
durch ihre charakteristische Eigenschaft eindeutig bestimmt.
Das war einleuchtend — eines der Dinge die Beweise vor allem sein sollten — und ist hoffentlich nicht sehr schwer nachzuvollziehen. Dennoch wollen wir die im vorhergehenden
Abschnitt eingeführten logischen Umformungsmöglichkeiten
anwenden. Denn einfache Sätze einer Theorie beweisen wir
nicht, um tiefgründige Erkenntnis zu erhoffen, sonder als
Prüfstein der Theorie. Naheliegende Aussagen sollten i.d.R.
auch in naheliegender Weise bewiesen werden können, wenn
die Theorie ein nützliches Ausdrucksmittel für das sein soll,
was sie modelliert. Wir setzen voraus
∀x : x 6∈ ;1
sowie
∀x : x 6∈ ;2
(∗)
und wir wollen daraus logisch folgern
∀x : x ∈ ;1 ⇔ x ∈ ;2
()
Wenden wir auf die vorstehende Formel die Äquivalenzregel
und Implikationsregel an, dann ergibt sich die zu () äquiva-
31
Literatur
lente Formel
∀x : (x 6∈ ;1 ∨ x ∈ ;2 ) ∧ (x 6∈ ;2 ∨ x ∈ ;1 )
(˜)
Nun müssen wir uns nur noch an die Oder-Einführung erinnern, um aus (∗) folgern zu können
∀x : x 6∈ ;1 ∨ x ∈ ;2 sowie ∀x : x 6∈ ;2 ∨ x ∈ ;1
Mit Hilfe der Und-Einführung und der Quantifikationsdistribution erhalten wir sofort ˜, das äquivalent zu ist. Was zu
beweisen war.
Mit diesen zwei der insgesamt zehn Axiome der Mengenlehre
ZFC, der einen Definition und dem einen Satz will ich es bewenden lassen. Sollte die Frage aufkommen, was denn nun
eine Menge eigentlich sei, so ist die vielleicht etwas unbefriedigende Antwort darauf: Eine Menge ist einer der Gegenständen, über die sich die axiomatisch definierten Aussagen der
zehn Axiome mache lassen. Und die Mengenlehre ist eine logische Untersuchung der Gegenstände auf die diese Aussagen
zutreffen.
Literatur
Den Anfang macht konkurrenzlos [KL96]. Für einen sanfteren Anstieg kann man nun zunächst [Buc98] und dann
[Lem65] wählen. Oder man geht gleich zum Meister [Tar66].
Zur Vertiefung eignen sich [HB68] und [Sho67]. Für eine Einführung in mathematische Methoden mit mehr Gewicht auf
der Philosophie empfehlen sich [Fre01] und [Fre09] sowie
etwas weniger archaisch [Rus02]. Eine auf das wesentliche
Literatur
32
beschränkte Mengenlehre für das mathematische Alltagsgeschäft ist in [Hal94] zu finden; etwas ausführlicher, umfassender und mit vielen historischen Bezügen wird man von
[Dei04] versorgt. Einen etwas anderen Blick auf die Mathematik ist in [Hil92] zu finden.
Literatur
[Aig06]
Martin Aigner. Diskrete Mathematik. 6. Aufl. Vieweg, 2006 (siehe S. 9).
[Buc98]
Theodor G. Bucher. Einführung in die angewandte
Logik. 2. Aufl. de Gruyter, 1998 (siehe S. 16, 31).
[Dei04]
Oliver Deiser. Einführung in die Mengenlehre. 2. Aufl.
Springer, 2004 (siehe S. 32).
[Fre01]
Gottlob Frege. Die Grundlagen der Arithmetik. Reclam, 2001 (siehe S. 31).
[Fre09]
Gottlob Frege. Die Grundgesetze der Arithmetik I/II.
Olms, 2009 (siehe S. 31).
[Hal94]
Paul R. Halmos. Naive Mengenlehre. 5. Aufl. Vandenhoeck und Ruprecht, 1994 (siehe S. 32).
[HB68]
D. Hilbert und P. Bernays. Grundlagen der Mathematik I. 2. Aufl. Springer, 1968 (siehe S. 31).
[Hil92]
David Hilbert. Natur und mathematisches Erkennen. Birkhäuser, 1992 (siehe S. 32).
[KL96]
Wilhelm Kamlah und Paul Lorenzen. Logische Propädeutik. 3. Aufl. Metzler, 1996 (siehe S. 31).
[Lem65] E. J. Lemmon. Beginning Logic. 2. Aufl. Chapman
& Hall/CRC, 1965 (siehe S. 31).
[Pei02]
Charles S. Peirce. Das Denken und die Logik des
Universums. Suhrkamp, 2002 (siehe S. 10).
[Rus02]
Bertrand Russell. Einführung in die mathematische
Philosophie. Meiner, 2002 (siehe S. 31).
[Sho67]
Joseph R. Shoenfield. Mathematical Logic. AddisonWesley, 1967 (siehe S. 31).
LITERATUR
[Tar66]
34
Alfred Tarski. Einführung in die mathematische Logik. 5. Aufl. Vandenhoeck & Ruprecht, 1966 (siehe
S. 16, 31).