7 Innovation und Marktstruktur

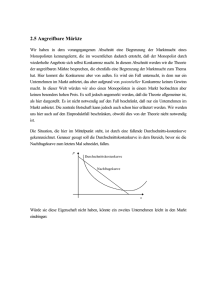
AVWL I Mikro (Sommer 2008)
7
7-1
Prof. Dr. M. Kocher
Innovation und Marktstruktur
Bisher haben wir die Produktionstechnologien stets als gegeben unterstellt. Unser Hauptaugenmerk galt der statischen Effizienz des Marktes und des Marktverhaltens von
Unternehmen, bei gegebenen Produktionsmöglichkeiten. In
diesem Abschnitt wollen wir uns mit der dynamischen Effizienz von Märkten beschäftigen, d.h. mit den Anreizen
von Unternehmen, in Forschung und Entwicklung zu
investieren.
Solow (1957) untersuchte, in welchem Umfang die Zunahme der Arbeitsproduktivität in den Vereinigten Staaten zwischen 1909 und 1949 auf eine Zunahme der Kapitalintensität zurückgeführt werden konnte. Er fand, dass die Zunahme der Kapitalintensität weniger als 20% der Produktivitätszunahme erklären konnte; der Rest musste an verbesserter Ausbildung der Arbeitskräfte und technologischem
Fortschritt liegen.
Denison (1985) schätzte, dass 68% der Produktivitätszuwächse in den Vereinigten Staaten zwischen 1929 und 1982
auf technologischen Fortschritt zurückzuführen sind, 34%
auf verbesserte Ausbildung und 22% auf die Realisierung
von Skalenerträgen.
c Sven Rady und Monika Schnitzer 2008
AVWL I Mikro (Sommer 2008)
7-2
Prof. Dr. M. Kocher
Technologischer Fortschritt ist somit als wichtigster Faktor
für Wachstum und eine Verbesserung der sozialen Wohlfahrt
zu sehen.
Eine heftig umstrittene Frage ist, welche Marktstruktur besonders günstig für die Förderung von technologischem Fortschritt, d.h. Forschung und Entwicklung ist.
Schumpeter (1942) argumentiert wie folgt:
What we have got to accept is that [the large-scale
establishment or unit of control] has come to be
the most powerful engine of [economic] progress...
In this respect, perfect competition is not only impossible but inferior, and has no title to being set up
as a model of ideal efficiency.
Schumpeters Argumentation, dass Monopole unter dem Gesichtspunkt statischer Effizienz nachteilig, unter dem Gesichtspunkt dynamischer Effizienz aber vorteilhaft sein können, spielt in der Wettbewerbspolitik eine wichtige Rolle.
Damit wird zu begründen versucht, warum vollständige Konkurrenz keine ideale Form des Wettbewerbs sei.
AVWL I Mikro (Sommer 2008)
7.1
7-3
Prof. Dr. M. Kocher
Marktstruktur und Innovationsanreiz
Typischerweise unterscheidet man zwei Typen von Innovationen, Produktinnovationen und Prozessinnovationen. Produktinnovationen bedeuten die Entwicklung neuer
Güter, Prozessinnovationen die Verbesserung der Produktionstechnologie und damit die Reduzierung der Produktionskosten.
In diesem Abschnitt untersuchen wir eine Frage, die von
Arrow (1962) aufgeworfen wurde:
Wie groß ist der Anreiz eine Unternehmens, eine
Prozessinnovation durchzuführen, die durch ein Patent geschützt, also keinem anderen Unternehmen
zugänglich ist?
Der Einfachheit halber bedienenen wir uns dabei eines Modells mit linearer Nachfrage und konstanten Grenzkosten
(die Resultate gelten jedoch auch für allgemeine Nachfrageund Kostenstrukturen):
• Nachfragefunktion: D(p) = 1 − p
• Konstante Stückkosten zwischen 0 und 1
AVWL I Mikro (Sommer 2008)
7-4
Prof. Dr. M. Kocher
7.1.1 Monopol
Monopolpreis und -gewinn bei Stückkosten von c:
1+c
pM (c) =
,
2
⎛
⎞
1 − c ⎟2
⎠
πM (c) =
2
⎜
⎝
Betrachten Sie nun eine Prozessinnovation, die die Stückkosten von c auf c < c reduziert.
Die niedrigeren Kosten ergeben einen höheren Gewinn:
⎛
⎞
1 − c ⎟⎟2
πM (c ) =
⎠ > πM (c)
2
⎜
⎜
⎝
Der Anreiz des Monopolisten zur Prozessinnovation ist gleich
dem Gewinnzuwachs:
1
VM = πM (c) − πM (c) = (1 − c)2 − (1 − c)2
4
Der Monopolist wird die Innovation genau dann durchführen,
wenn der Gewinnzuwachs VM die Kosten der Implementierung übersteigt.
AVWL I Mikro (Sommer 2008)
7-5
Prof. Dr. M. Kocher
7.1.2 Sozialer Planer
Ein sozialer Planer maximiert die soziale Wohlfahrt, indem
er den Preis gleich den Grenzkosten setzt.
Bei Stückkosten von c ist die soziale Wohlfahrt (Summe aus
Produzenten- und Konsumentenrente):
(1 − c)2
2
Bei Stückkosten von c ist die soziale Wohlfahrt:
(1 − c)2
2
Der Anreiz des sozialen Planers zur Prozessinnovation ist
gleich dem Zuwachs der sozialen Wohlfahrt:
1
VS = (1 − c)2 − (1 − c)2 > VM
2
Beachten Sie:
Der Monopolist hat im Vergleich zum sozialen Planer einen
zu geringen Anreiz, in die Innovation zu investieren, ist also
dynamisch ineffizient.
Warum ist das so?
AVWL I Mikro (Sommer 2008)
7-6
Prof. Dr. M. Kocher
7.1.3 Bertrand-Wettbewerb
Angenommen, N Unternehmen produzieren ein homogenes
Gut zu Stückkosten c. Bertrand-Wettbewerb führt dann zu
einem Gleichgewichtspreis pB = c.
Um die Innovationsanreize zu untersuchen, müssen wir zwei
Fälle unterscheiden:
• Fall 1: Drastische Innovation
pM (c) < c
In diesem Fall kann eine Unternehmung, die mit Stückkosten c produziert, den Monopolpreis setzen und den
gesamten Markt bedienen, ohne den Preiswettbewerb
der Konkurrenten fürchten zu müssen.
• Fall 2: Nichtdrastische Innovation
pM (c) ≥ c
In diesem Fall bedient die Unternehmung mit Stückkosten c wiederum den ganzen Markt, allerdings nur zum
Preis p = c − (beliebig nahe an c).
AVWL I Mikro (Sommer 2008)
7-7
Prof. Dr. M. Kocher
Fall 1: Drastische Innovation
Die Innovation ist drastisch genau dann, wenn:
1 + c
< c ⇔ c < 2c − 1
pM (c ) =
2
In diesem Fall ist der Anreiz zur Innovation gegeben durch:
VBd = πM (c) − 0 = πM (c) > πM (c) − πM (c) = VM
Ein Monopolist erzielt schon vor der Innovation einen positiven Gewinn, während ein Unternehmen bei BertrandWettbewerb vor der Innovation Nullgewinne erzielt. Da ein
Monopolist durch die Innovation weniger zu gewinnen hat,
ist sein Innovationsanreiz niedriger.
Ferner gilt :
1
1
(1 − c)2 − (1 − c)2 − (1 − c)2
2
4
1
1
= (1 − c)2 − (1 − c)2
4
2
1
1
> (1 − [2c − 1])2 − (1 − c)2
4
2
1
= (1 − c)2 − (1 − c)2 > 0
2
VS − VBd =
AVWL I Mikro (Sommer 2008)
7-8
Prof. Dr. M. Kocher
Auch bei Bertrand-Wettbewerb ist der Innovationsanreiz also kleiner als der eines sozialen Planers. Warum ist das so?
Ergebnis:
VM < VBd < VS
Fall 2: Nichtdrastische Innovation
Die Innovation ist nichtdrastisch genau dann, wenn:
1 + c
pM (c ) =
≥ c ⇔ c ≥ 2c − 1
2
Da der Preis p beliebig nahe an c heran gehoben werden kann, ist der Innovationsanreiz in diesem Fall gegeben
durch:
VBnd = (c − c)D(c) − 0 = (c − c)(1 − c)
Vergleich mit dem Monopolisten:
1
(1 − c)2 − (1 − c)2
VM =
4
1
= (c − c)(2 − c − c)
4
1
≤ (c − c)(2 − c − [2c − 1])
4
3
= (c − c)(1 − c) < VBnd
4
AVWL I Mikro (Sommer 2008)
7-9
Prof. Dr. M. Kocher
Vergleich mit dem sozialen Planer:
1
VS = (1 − c)2 − (1 − c)2
2
1
= (c − c)(2 − c − c)
2
>
1
(c − c)(2 − 2c) = VBnd
2
Wieder finden wir, dass der Innovationsanreiz eines BertrandWettbewerber größer ist als der eines Monopolisten, aber
kleiner als der eines sozialen Planers:
VM < VBnd < VS
Ergebnis:
Nicht nur bei gegebener Technologie (statisch), sondern
auch im Hinblick auf Innovationsanreize (dynamisch) ist
Wettbewerb einem Monopol vorzuziehen.
AVWL I Mikro (Sommer 2008)
7.2
7-10
Prof. Dr. M. Kocher
Wettbewerb um ein Patent
Nun wollen wir untersuchen, wie sich die Marktstruktur entwickelt, wenn mehrere Unternehmen um das Patent für eine
Prozessinnovation konkurrieren können.
Wir betrachten den Fall eines Monopolisten, der durch potentiellen Wettbewerb bedroht ist. Der potentielle Konkurrent hat zunächst prohibitiv hohe Produktionskosten und
kann deshalb nur dann auf den Markt kommen, wenn er
ein Patent erwirbt, das die Reduktion der Kosten erlaubt.
Wenn er das Patent erwirbt und auf den Markt kommt,
konkurrieren er und der Monopolist als Duopolisten.
Frage:
Wenn das Patent von einer dritten Partei gehalten
und dem Meistbietenden zum Verkauf angeboten
wird, wer wird es dann erwerben – der Monopolist
oder der potentielle Konkurrent?
In die Entscheidung des Monopolisten muss nun eingehen,
dass das Patent an den Konkurrenten fallen wird, falls er
selbst es nicht erwirbt. Dies verändert die Anreize im Vergleich zum vorigen Abschnitt.
AVWL I Mikro (Sommer 2008)
7-11
Prof. Dr. M. Kocher
Monopolist:
• Erwirbt er das Patent, ist sein zukünftiger Gewinn πM (c).
• Erwirbt nicht er, sondern der potentielle Konkurrent das
Patent, ist sein zukünftiger Duopolgewinn πD (c, c).
(In diesem Fall produziert der Konkurrent mit Stückkosten c und der Monopolist mit Stückkosten c > c.)
• Der Innovationsanreiz des Monopolisten ist demnach:
VM = πM (c) − πD (c, c)
Potentieller Konkurrent:
• Erwirbt er das Patent, ist sein zukünftiger Gewinn πD (c, c).
• Erwirbt nicht er, sondern der Monopolist das Patent, ist
sein zukünftiger Gewinn 0.
• Sein Innovationsanreiz ist demnach:
VK = πD (c, c)
Beachten Sie:
• Bei homogenen Gütern gilt (“Effizienzeffekt”):
πM (c) ≥ πD (c, c) + πD (c, c)
Warum?
AVWL I Mikro (Sommer 2008)
7-12
Prof. Dr. M. Kocher
Ergebnis:
• Bei Wettbewerb um ein Patent hat der Monopolist einen
stärkeren Anreiz, das Patent zu erwerben, als der potentielle Konkurrent:
VM ≥ VK
• Der Anreiz, Monopolist zu bleiben, ist größer als der
Anreiz, Duopolist zu werden. Im Englischen nennt man
diesen Effekt persistence of monopoly.
Beachten Sie außerdem:
• Angenommen, das Patent beinhaltet eine Technologie,
die der des Monopolisten nicht überlegen ist. In diesem
Fall hat der Monopolist dennoch einen Anreiz, es zu
erwerben (und dann ungenutzt zu lassen). Der einzige
Grund für den Erwerb ist, den Marktzugang des potentiellen Konkurrenten zu verhindern.
• Ähnliches ist möglich, wenn das Patent eine Produktinnovation zum Inhalt hat, die dem vom Monopolisten
produzierten Gut relativ ähnlich ist. Wieder hat der Monopolist einen Anreiz, das Patent zu erwerben, um den
Konkurrenten vom Markt fernzuhalten. Ob er selbst das
Patent nutzt, hängt aber davon ab, wie hoch die Kosten
der Markteinführung sind im Vergleich zum Nachfragezuwachs aufgrund der höheren Produktvielfalt.