Praktikumsversuch der Mikrowellentechnik

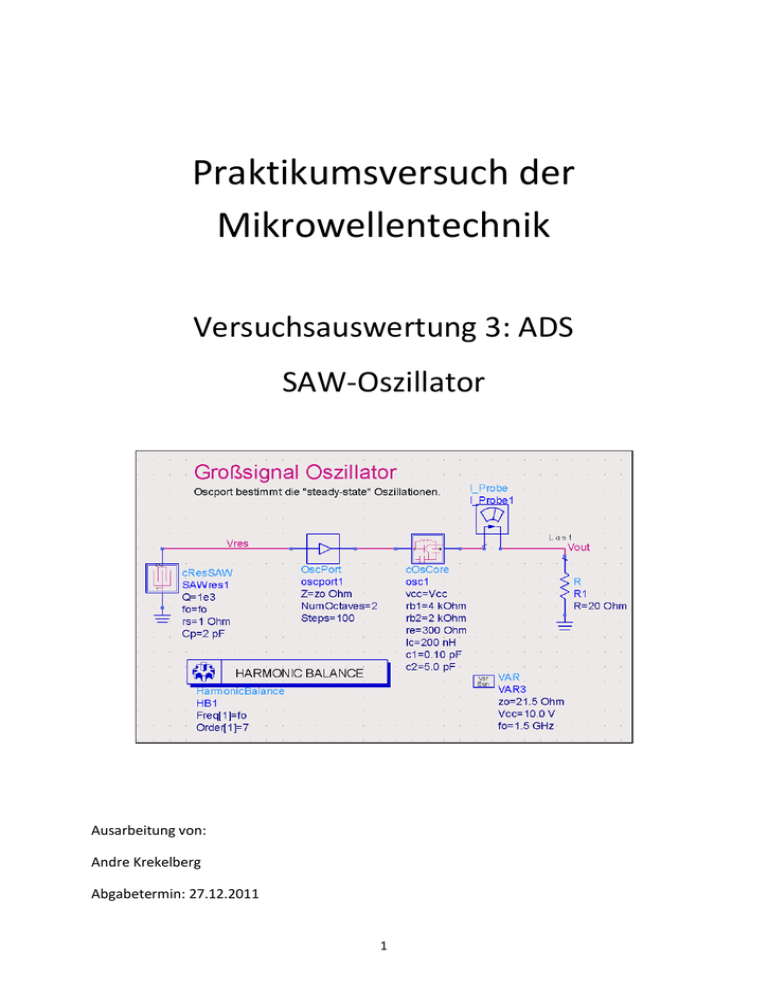
Praktikumsversuch der
Mikrowellentechnik
Versuchsauswertung 3: ADS
SAW-Oszillator
Ausarbeitung von:
Andre Krekelberg
Abgabetermin: 27.12.2011
1
1.
Versuchsbeschreibung
Das Ziel dieses Praktikums ist das Simulieren und Dokumentieren einer vorgegebenen
Schaltung mit Hilfe der Software ADS. Die Titel der erhaltenden Messergebnisse sollen
anschließend ins Deutsche übersetzt werden. In dieser Dokumentation wurde ein SAWOszillator bearbeitet. Da sich das gesamte Beispielprojekt über neun verschiedene
Simulationen erstreckt, kann nicht auf jede dieser Simulationen im Detail eingegangen
werden.
Die folgenden Simulationen wurden durchgeführt und dokumentiert:
1. Fixed Frequency Oscillator (Oszillator mit fester Frequenz)
2. Frequency Pulling (Fehlanpassung des Ausgangs)
3. Frequency Pushing (Schwankung der Versorgungsspannung)
4. Output Load Mapping (Abbildung der Ausgangsbelastbarkeit)
5. Input Load Mapping (Abbildung der Eingangslast)
6. Stability via Nyquist Plot (Stabilität des Schwingungsverhaltens)
7. Single Frequency Dynamik Display (Oszillatordynamik für eine feste Frequenz)
8. Large Signal S-Parameter (Großsignal S-Parameter)
9. Single Frequency Phase Noise (Phasenrauschen bei einer bestimmten Frequenz)
2.
2.1
Versuchsbeschreibungen und Auswertungen
Versuch „Oszillator mit fester Frequenz“
Der SAW-Oszillator (Surface Acoustic Wave, Oberflächenwellen) besteht im Wesentlichen
aus einem SAW-Resonator, dem Oszillatorport und dem Oszillatorkern. Für diese Simulation
wurden weiterhin ein Strommessgerät und ein Abschlusswiderstand verwendet. Die
Beschreibung „Harmonic Balance“ in der Umrandung unten links zeigt die verwendete
Simulationsart an.
2
SAW-Resonatoren haben durch Ihren physikalischen Aufbau die Eigenschaft bei Ihrer
definierten Resonanz auch für sehr hohe Frequenzen in der Grundschwingung zu schwingen.
Das Oszillatorport OscPort fungiert als Einrichtung um reelle Bedingungen für die Simulation
zu schaffen. Im Folgenden ein kurzer Auszug aus der Modulbeschreibung:
This is a special device used for an oscillator analysis.
3
Der Oszillatorkern besteht aus einer aktiven Stufe, die über eine frequenzselektive Stufe
rückgekoppelt ist.
Als aktives Element wird eine einstufige Transistorschaltung (Basisschaltung) verwendet.
Diese hat die Eigenschaft, durch nichtlineares Verhalten für eine Amplitudenstabilisierung zu
sorgen. Für die Phasenbedingung ist das rückkoppelnde Netzwerk von entscheidender
Bedeutung.
Diese Baugruppe wird in den folgenden Simulationsaufbauten in identischem Aufbau
verwendet.
Die ermittelten Simulationsergebnisse:
4
Die Simulation wurde bei 1.524GHz im HarmonicBalance-Verfahren durchgeführt. Im oberen
linken Plot ist das Frequenzspektrum als Verhältnis von Eingangsspannung Vres zu
Ausgangsspannung Vout im Frequenzbereich abgebildet. Zu sehen ist, dass die Spannung mit
steigender Frequenz sinkt. Rechts oben sind die gleichen Spannungen im Zeitbereich
abgebildet. Dort kann man das Schwingverhalten des Oszillators verfolgen.
Die Werte in der Mitte des Bildes wurden automatisch berechnet und geben neben dem
Leistungsverlust der Schaltung auch die Ausgangsleistung der Grundschwingung in Watt und
dBm an.
Die Plots darunter zeigen die Spannungen (Kollektor, Basis und Emitter) des Transistors in
dem Oszillatorkern an. Als letztes ist die Eingangs- zu Ausgangsleistung im Frequenz- und
Zeitbereich abgebildet.
2.2
Versuch „Frequenz Pulling“
Die Vorgehensweise des Versuchs Frequency Pulling ist das bewusste Fehlanpassen der
Ausgangslast und gleichzeitige Auswerten der damit verbundenen Frequenzabweichung. Die
Lastphase wird dabei im Bereich von 0 bis 2*π variiert.
Zusätzlich kommt hier ein Pufferverstärker cAmpBuffS zum Einsatz, dessen innerer Aufbau in
der folgenden Abbildung beschrieben ist.
5
Die ermittelten Simulationsergebnisse:
Der linke Plot zeigt den Zusammenhang zwischen der variierten Last (0 – 2* π) und der
ermittelten Frequenzabweichung an. Dabei ist eine nur sehr geringe und nicht ablesbare
Abweichung zu verzeichnen.
Im unteren Plot ist der Betrag der Ausgangsspannung über die Verstimmung der Last
dargestellt.
6
2.3
Versuch „Frequenz Pushing“
Bei diesem Versuch wird nicht die Last, sondern die Versorgungsspannung verändert und
dabei die Abweichung der Frequenz aufgenommen.
Die ermittelten Simulationsergebnisse:
Im Plot oben links ist die Frequenz in Abhängigkeit von der Abweichung der
Versorgungsspannung aufgezeichnet. Im Plot daneben ist der Bereich zwischen den Markern
im vorherigen Bild vergrößert angezeigt. Zu erkennen ist eine Frequenzabweichung von
0,8MHz im Bereich von 7,4V bis 9,8V. Im unteren Plot ist die Ausgangsspannung im Bezug
auf die Versorgungsspannung abgebildet. Eine Amplitudenabweichung von ca. 14 dB ist
abzulesen.
7
2.4
Versuch „Abbildung der Ausgangsbelastbarkeit“
Um eine Abbildung der Last zu simulieren wird der Eingang des Oszillatorkerns mit einem
Terminierungswiderstand auf Masse gelegt und der Ausgang mit einer variierbaren Last
beschaltet. Der Widerstand definiert die Portimpedanz. Es wird von 1-2 GHz gesweept.
Die ermittelten Simulationsergebnisse:
Nach Ausführung der Simulation können mit Hilfe einer interaktiven Ergebnisseite die
Messergebnisse nachgespielt werden. Durch Positionsveränderung der Marker in den beiden
folgenden Smith Charts können Ein- und Ausgangswiderstand verändert werden. Zusätzlich
kann durch Bewegung des FRQ-Markers die Frequenz variiert werden.
8
2.5
Versuch „Abbildung der Eingangslast“
Hierbei werden die Reflexionskoeffizienten des Ausgangs für verschiedene Terminierungen
simuliert indem der Oszillatorkern mit einem variierbaren Eingangswiderstand und einem
Terminierungswiderstand beschaltet wird.
Die ermittelten Simulationsergebnisse:
Hier können wiederrum mit Hilfe einer interaktiven Ergebnisseite die Messergebnisse
nachgespielt werden. Durch Positionsveränderung der Marker Zs und Zout können die
Beziehungen des Ausgangs zur Eingangslast simuliert werden.
9
3.6
Versuch „Stabilität des Schwingungsverhaltens“
In diesem Versuch wurde die Stabilität des Schwingungsverhaltens des Oszillators mit Hilfe
der Nyquistdarstellung ermittelt.
Die ermittelten Simulationsergebnisse:
Der linke Plot bietet eine Darstellung mit Nyquist-Ortskurve. Rechts daneben sind Betrag und
Phase in Abhängigkeit der Frequenz aufgetragen.
10
2.7
Versuch „Darstellung der Dynamik bei einer festen Frequenz“
Mit dieser Simulation wird die Dynamik des Oszillators dargestellt.
Die ermittelten Simulationsergebnisse:
Im linken Plot ist die Spannung Vce über die Zeit und im rechten Plot der Strom Ic über die
Zeit abgebildet. Zu erkennen ist, dass die Spannung (währende der Transistor durchschaltet)
abnimmt, während der Strom im gleichen Moment deutlich zunimmt. Im unteren Plot
wurden diese beiden Ergebnisse noch einmal überlagert dargestellt.
11
2.8
Versuch „Großsignal S-Parameter“
Die Frequenz und die Leistung der Oszillatoren werden von den S-Parametern bestimmt. Für
diese Simulation wird der Eingang des Oszillatorkerns über ein Strommessgerät auf eine
Quelle gelegt, die durch Variation der Frequenz fr und der Variablen VS eingestellt werden
kann.
Die ermittelten Simulationsergebnisse:
Der Kurokawa-Plot dient in dieser Simulation als Anzeigeinstrument. Die Werte der Größen
fr und der Variablen VS können hier durch Verschieben von Markern verändert werden,
wodurch sich die Graphen in den beiden Plots verändern. Der linke Plot zeigt das 1/Sn im
Bezug auf die Amplitude einer bestimmten Eingangsfrequenz an. Der Plot daneben zeigt das
1/Sn in Bezug auf eine Frequenz bei einem bestimmten Quellpegel an.
12
2.9
Versuch „Phasenrauschen bei einer bestimmten Frequenz“
Um das Phasenrauschen zu simulieren wurde das Rauschen über den Frequenzbereich von
10Hz bis 1MHz durchlaufen. Die Grundfrequenz fo wurde auf 1.5GHz gesetzt.
13
Die ermittelten Simulationsergebnisse:
In den folgenden Plots wurde das Phasen- und Amplitudenrauschen für Vres und Vout über
den Frequenzbereich geplottet. Deutlich zu erkennen sind die fallenden Kurven in beiden
Diagrammen bei steigender Frequenz. Für die Oszillatorfrequenz von 1.524GHz wurden die
Simulationswerte tabellarische aus den Diagrammen der Phasen- und Amplitudenrauschen
dargestellt. Der größte signifikante Beitrag des Rauschens ergibt sich im Bereich von 15dB.
(oben rechts angezeigt)
3 Fazit
Dieses Praktikum bat in recht kurzer Zeit einen guten Einblick in die Funktionalität und
verschiedenen Simulationsmöglichkeiten des Programms ADS. Aufgrund der vorgefertigten
Beispielsimulationen war es möglich sich in diesem Zeitrahmen effektiv und schnell mit den
Simulationsmethoden vertraut zu machen.
14