1 Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1

1
Matur-/Abituraufgaben Analysis
√
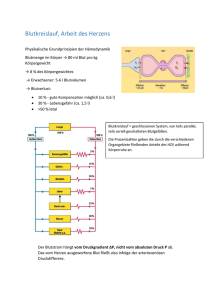
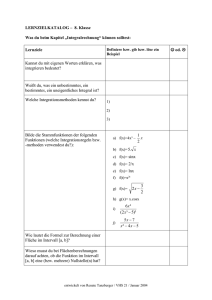
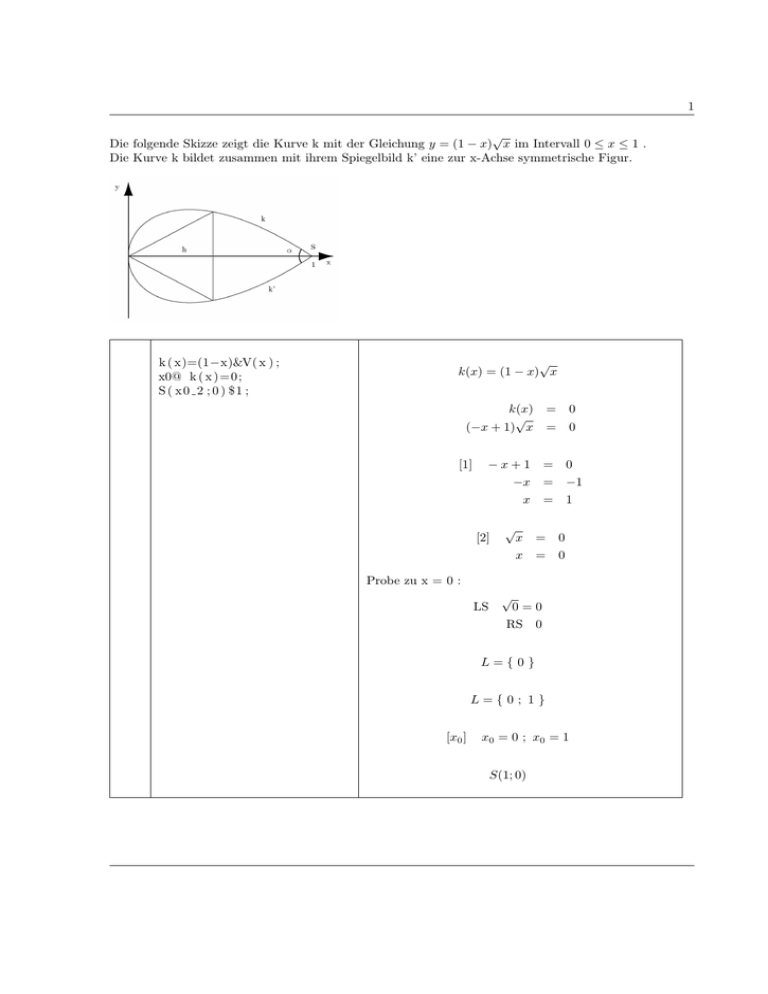
Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 − x) x im Intervall 0 ≤ x ≤ 1 .
1. Tropfen
p
Die folgende Skizze zeigtDie
die Kurve
k mitkder
Gleichung
y = (1 x) mit
x im ihrem
Intervall Spiegelbild
0  x  1. Die k’ eine zur x-Achse symmetrische Figur.
Kurve
bildet
zusammen
Kurve k bildet zusammen mit ihrem Spiegelbild k’ eine zur x-Achse symmetrische Figur.
(a) Wie gross ist der Winkel ↵ bei der Spitze S?
(b) Welches ist die grösste Breite (parallel
zur y-Achse gemessen)
k ( x)=(1−x)&V(
x )des
; Tropfens?
(c) Bei der Rotation der Kurve k um x0@
die x-Achse
k ( entsteht
x )=0;ein 3-dimensionaler tropfenförmiger Körper.
Wie gross ist sein Volumen?
S ( x 0 2 ; 0 ) $1 ;
√
k(x) = (1 − x) x
(d) Diesem Körper wird ein Kreiskegel mit der Spitze im Ursprung und der Höhe h auf der x-Achse
einbeschrieben (vgl. Skizze). Für welche Höhe h wird das Volumen des Kegels maximal?
2. Untersuchungen
Gegeben ist die Funktion f (X) = (2x
k(x) = 0
√
(−x + 1) x = 0
1) · eax , mit a 2 IR.
(a) Gesicht sind die Nullstellen, Extremal- und Wendestellen der Funktion.
(b) Wie gross ist die Fläche, die f (x) mit der x-Achse einschliesst?
[1]
(c) Für welchen Wert von u (u < 0) hat das Dreieck mit den Eckpunkten O( 0 | 0 ), P ( u | 0 ) und
Q( u | f (u) ) maximalen Flächeninhalt?
−x+1
=
x
=
−x
3. Kurvendiskussion, Rotationskörper und ein Extremum
p
Für jeden Parameterwert a > 2 ist durch f (x) = a x 2 a x eine Kurve gegeben.
(a) Diskutiere und skizziere die Kurve für a = 3. Verlangt sind Definitionsbereich, Nullstellen und
Hochpunkt.
[2]
√
(b) Die Fläche zwischen der Kurve und der x-Achse rotiert um die x-Achse. Berechne das Volumen
des entstehenden Rotationskörpers in Abhängigkeit des Parameters a.
(c) Bestimme a > 2 so, dass das Volumen des vorher berechneten Rotationskörpers extremal wird.
Handelt es sich um ein Minimum oder um ein Maximum?
Probe zu
0
= −1
1
x =
0
x =
0
x=0:
4. Polynomfunktion 3. Grades
Eine Poynomfunktion 3. Grades hat im Ursprung einen Wendepunkt und geht durch die Punkte
A( 1 | 3 ) und B( 2 | 0 ).
LS
√
0=0
RS
(a) Wie lautet die Funktionsgleichung?
0
(b) Welche Gleichung hat die Wendetangente?
L={0}
L={0; 1}
[x0 ]
x0 = 0 ; x0 = 1
S(1; 0)
2
a
Wie gross ist der Winkel α bei der
Spitze S?
√
Ableitung von k(x) = (−x + 1) x
u = −x + 1
u0 = −1
√
1
√
v= x
v0 =
2· x
√
1
k 0 (x) = − x + (−x + 1) √
2· x
k ’ @ak$−;
@@D;
m2=k ’ ( 1 ) ;
&a =2∗| a r c t a n (m2 ) | ;
√
m2 = k 0 (1) = − 1 + (−1 + 1)
1
√
2· 1
1
1
= −1 + (−1 + 1)
= −1 + (−1 + 1)
2·1
2
1
= −1 + 0 · = −1 + 0 = −1
2
α = 2 · |arctan(m2)| = 2 · |arctan(−1)| = 2 · | − 45|
= 2 · 45 = 90
b
Welches ist die grösste Breite (parallel zur y-Achse gemessen) des
Tropfens?
x1@ k ’ ( x)<>0;
b=2∗k ( x1 ) ; % ;
wesentlich einfachere Lösung :
−2 ·
√
x·
√
k 0 (x) <> 0
√
1
− x + (−x + 1) √ <> 0
2· x
√
1
− x + (−x + 1) √
2· x
√
x
x + (−x + 1) = 0
−3x = −1
1
x=
3
=
0
=
(x − 1)
1
√ )2
x
1
x = (x2 − 2x + 1)( √ )2
2· x
1
x = (x2 − 2x + 1)
4·x
1
x = (x2 − 2x + 1)
4x
x2 − 2x + 1
x =
4x
(x − 1)2 · (
x =
Nenner :
2·
4x
x · 4x
4x
2
3x2 + 2x − 1
2
3x + 2x
= x2 − 2x + 1
= x2 − 2x + 1
=
0
=
1
2·
1
√
x
3
2
x2 + x
3
2
1 2
2
x + x+( )
3
3
1
(x + )2
3
1
x+
3
x
Probe zu x = −1 :
LS
−
√
−1 + (1 + 1)
1
3
1 1
=
+
3 9
4
=
9
2
= ±
3
=
= −1 ; x =
1
√
1
3
= @ + (1 + 1)
1
2·@
2 · −1
1
1
= @ + (1 + 1) = @ + 2 ·
=@+2·@=@+@=@
@
@
RS 0
Probe zu x =
1
3
:
r
LS
−
1
1
1
1
1
1√
√
+ (− + 1) q = −
3 + (− + 1)
1
3
3
3
3
2 · ( 3 3)
2· 1
3
1√
1
1
1√
2
1
=−
3 + (− + 1) 2 √ = −
3 + · 2√
3
3
3
3
3 3
3 3
1√
2 1√
1√
1√
=−
3+ ·(
3) = −
3+
3=0
3
3 2
3
3
RS 0
L={
+]
[x1 ]
1
}
3
1
[−
3
x1 =
1
3
Warnung : Definitionsmenge?
"
r #
1
1
1
1
1√
b = 2 · k(x1 ) = 2 · k( ) = 2 (− + 1)
= 2 (− + 1) · (
3)
3
3
3
3
3
2√
1
2√ 2
4√
=
3(− + 1) =
3· =
3
3
3
3
3
9
4
b =
c
Bei der Rotation der Kurve k
um die x-Achse entsteht ein
3-dimensionaler
tropfenförmiger Körper. Wie gross ist sein
Volumen?
k ” ( x)=−k ( x ) $g ;
V@IXk [ 0 ; 1 ] ; % ;
0, 770
√
k 00 (x) = −k(x) = −(−x + 1) x
Volumen zu k bei Rotation um die x-Achse
von 0 bis 1
√
q(x) = ((−x + 1) x)2 = (x2 − 2x + 1)x = x3 − 2x2 + x
Stammfunktion zu q(x) = x3 − 2x2 + x
q0 (x) =
1 4 2 3 1 2
x − x + x
4
3
2
q0 (0) = 0
1
1 2 1
q0 (1) = − + =
4 3 2
12
V = π(
1
1
1
− 0) = π ·
=
π
12
12
12
V =
V
d
Diesem Körper wird ein Kreiskegel mit der Spitze im Ursprung und
der Höhe h auf der x-Achse einbeschrieben (vgl. Skizze). Für welche
Höhe h wird das Volumen des Kegels maximal?
v ( x)=1/3&P ∗ [ k ( x ) ˆ 2 ] ∗ x$c ;
v ’ @av$−;
x2@ v ’ ( x)<>0;
v ( x2 2 );%;
1
π
12
=
0, 262
√ 2
1 1
π · k(x)2 · x = π · (−x + 1) x · x
3
3
√ 2
1
1 = πx · (−x + 1) x = πx (x2 − 2x + 1)x
3
3
1 2 2
1 4 2 3 1 2
= πx (x − 2x + 1) = πx − πx + πx
3
3
3
3
v(x) =
Ableitung von v(x) = 13 πx4 − 23 πx3 + 31 πx2
v 0 (x) =
4 3
2
πx − 2πx2 + πx
3
3
v 0 (x) <> 0
4 3
2
πx − 2πx2 + πx <> 0
3
3
2
πx(2x − 1)(x − 1) =
3
0
5
1
; 1}
2
L={0;
1
[−]1[+
2
−]0[+]
[x2 ]
x2 = 0 ; x2 =
1
; x2 = 1
2
1
1
1
1
1
v( ) =
π− π+ π=
π
2
48
12
12
48
≈ 0, 0654
r=k ( 0 , 5 ) ; % ;
O( 0 ; 0 ) ;
P1 ( 0 , 5 ; r ) ;
P2 (0 ,5; − r ) ;
@@ OP1$r ;
@@ P1P2$r ;
@@ P2O$r
r = k(0, 5) = (−0, 5 + 1)
r
P1 (0, 5; r)
P2 (0, 5; −r)
1/2
1/10
1/10
-1/2
1/2
S
1
p
1√
0, 5 = (−0, 5 + 1) · (
2)
2
1√
1√
=
2 · 0, 5 =
2
2
4
=
0, 354
O(0; 0)
1√
P1 (0, 5;
2)
4
1√
P2 (0, 5; −
2)
4