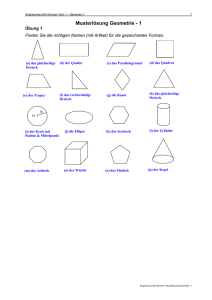
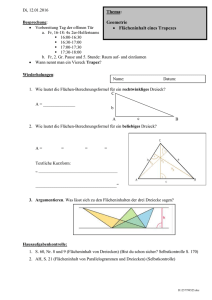
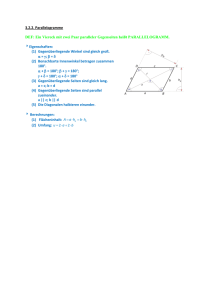
parallel heißt auch
Werbung

4.1 Parallelogramm
Mathematik
7 – G8
Ein Viereck,Grundwissen
bei dem je zwei
Gegenseiten
Ortenburg-Gymnasium Oberviechtach
parallel sind, heißt Parallelogramm.
4 Besondere Vierecke
Grundwissen Mathematik
7 – G8
Jede der3. folgenden
Aussagen ist gleichwertig:
1. Innenwinkel bei Dreiecken und Vierecken
Besondere
Vierecke
4.1 Parallelogramm
ist punktsymmetrisch.
Grundwissen Mathematik
7 – G8 • Das Parallelogramm
Ein Viereck, bei
dem je zwei Gegenseiten
Die Summe der (Innen-)Winkel ergibt in jedem Dreieck 180°, in jedem Viereck 360°.
a) Besondere
Parallelogramm:
4
Vierecke
• Im Parallelogramm
halbieren
sichparallel
die Diagonalen
gegenseitig.
Ein
Viereck,
bei
dem
je
Gegenseiten
sind, heißt Parallelogramm.
parallel sind, heißtzwei
Parallelogramm.
4.1 Jede
Parallelogramm
3 Besondere Dreiecke
Sonderfälle:
derder
folgenden
Aussagen
ist gleichwertig:
2. Besondere Dreiecke
Jede
folgenden
Aussagen
ist gleichwertig:
• Das Parallelogramm ist punktsymmetrisch.
Die
Raute
ist
ein
Parallelogramm
mit
4 gleich langen Seiten.
Ein Viereck,
bei demhalbieren
je zwei
Parallelogramm
istGegenseiten
punktsymmetrisch.
• • ImDas
Parallelogramm
sich
die Diagonalen
3.1 Das gleichschenklige Dreieck
a) Das gleichschenklige Dreieck:
• gegenseitig.
Im
halbierenmit
sich 4die
Diagonalen
gegenseitig.
parallel
sind,
heißt
Parallelogramm.
Das Rechteck
ist Parallelogramm
ein
Parallelogramm
gleich
großen
Ein
mit zwei
gleich gleich
langen Seiten
(Schenkel)
EinDreieck
Dreieck
mit zwei
langen
Seiten heißt
gleichschenklig. Die dritte Seite heißt Basis.
Sonderfälle:
Winkeln.
(Schenkel)
heißt halbiert
gleichschenklig.
Die dritte Seite
Jede •Sonderfälle:
der
Aussagen ist
Die
Höhe im Dreieck
die Basis (Mittelsenkrechte)
Diefolgenden
Raute istist
einein
Parallelogramm
mit gleichwertig:
vier gleich
Seiten.
Die
Raute
Parallelogramm
mit4 4langen
gleich
langen
Seiten.
und
halbiert
den Winkel γ
heißt
Basis.
Das Quadrat
ist
ein
Parallelogramm
mit
gleich
langen
•
Das
Rechteck
ist
ein
Parallelogramm
mit
vier
gleich
großen
Winkeln. Seiten
• Das
Parallelogramm
ist
punktsymmetrisch.
istParallelogramm
ein Parallelogramm
mitlangen
4 gleich
• Das
Das Rechteck
Quadrat ist ein
mit vier gleich
Seitengroßen
und vier gleich
und 4 gleich
großen
Winkeln.
Jede
folgenden
Aussagen
ist gleichwertig:
Jedederder
folgenden
Aussagen
ist gleichwertig:
• ImWinkeln.
Parallelogramm
halbieren sich die Diagonalen gegenseitig.
großen Winkeln.
7. Klasse Grundwissen
#
•• Das
Dreieck
ist gleichschenklig.
Das
Dreieck
ist gleichschenklig.
• Das Dreieck ist achsensymmetrisch bezügl. der Höhe.
Das
Dreieck
achsensymmetrisch.
•• Das
Dreieck
besitztist
zwei
gleich große Basiswinkel.
!
Basis
• Das Dreieck besitzt zwei gleich große
Winkel.
3.2 Das gleichseitige Dreieck
b) Das gleichseitige Dreieck:
Ein
mit drei
langen Seiten
heißtSeiten
EinDreieck
Dreieck
mit gleich
drei gleich
langen
gleichseitiges Dreieck. Seine Innenwinkel betragen
heißt 60°.
gleichseitig. Seine Innenwinkel
jeweils
betragen jeweils 600.
Das Quadrat ist ein Parallelogramm mit 4 gleich langen Seiten
Sonderfälle:
und 4 ist
gleich
Winkeln. mit 4 gleich langen Seiten.
Die Raute
ein großen
Parallelogramm
4.2 Trapez
Dasb) Rechteck
ist ein Parallelogramm mit 4 gleich großen
Trapez:
Basis
Ein
Viereck,
bei
dem zwei Seiten parallel sind, heißt
Winkeln.
4.2
Trapez.
Ein Viereck,
beiTrapez
dem zwei Seiten parallel
Das Quadrat ist ein Parallelogramm mit 4 gleich langen Seiten
60°
sind, heißt Trapez.
Ein
Viereck,
bei Winkeln.
dem
zwei
Seiten
achsensymmetrisches
Trapez
heißt
auch parallel
und 4Ein
gleich
großen
gleichschenkliges Trapez.
"
60°
3.3 Das rechtwinklige Dreieck
c) Das rechtwinklige Dreieck:
Ein
ABCABC
hat genau
dann beidann
C einen
EinDreieck
Dreieck
hat genau
beirechten
C
Winkel,
wenn C auf
dem Halbkreis
[AB]
liegt
einen rechten
Winkel,
wennüber
C auf
dem
(Thaleskreis).
Halbkreis über [AB] liegt. (Thaleskreis)
Die Schenkel des rechten Winkels sind die
Die Schenkel
des rechten
Winkels
sind
Katheten,
die Gegenseite
des rechten
Winkels
ist
dieHypothenuse
Katheten,(längste
die Gegenseite
des
die
Seite).
rechten Winkels ist die Hypotenuse (längste Seite).
sind, heißt Trapez.
Ein achsensymmetrisches
Trapez heißt auch
Ein achsensymmetrisches
Trapez heißt auch
gleichschenkliges
Trapez.
60°
gleichschenkliges Trapez.
4.2 Trapez
Ein Viereck, bei dem zwei Seiten parallel
c) Drachenviereck:
4.3 Drachenviereck
4.3 Drachenviereck
sind, heißt Trapez.
Ein Viereck heißt Drachenviereck, wenn es eine
Symmetrieachse
Gegenecken
Ein Viereck durch
heißtzwei
Drachenviereck,
achsensymmetrisches
Trapez hat.
heißtwenn
auches
Ein heißt Drachenviereck, wenn es
Ein Viereck
eine Symmetrieachse
durch zwei Gegenecken
gleichschenkliges
Trapez.
eine Symmetrieachse
durch
zwei
Gegenecken
hat.
hat.
4.3 Drachenviereck
Seite 4 von 12
Seite 4 von
12
Ein Viereck
heißt Drachenviereck, wenn es
Seite 3 von 12
eine Symmetrieachse durch zwei Gegenecken
hat.
7 – G8
Grundwissen Mathematik
9 Lineare Gleichungen
4. Termumformungen
a) Gleichartige Termglieder zusammenfassen:
Beispiele:
x − y2 + 2x + y2 = x + 2x − y2 + y2 = 3x
5. Lineare
Die Lösungsmenge
einer Gleichungen
Gleichung ändert sich nicht, wenn man
auf beiden Seiten
Zahl oder
Die dieselbe
Lösungsmenge
einerdenselben
Gleichung Term
ändert addiert
sich nicht, wenn man auf beiden Seiten
dieselbe
Zahl oder
denselben
Term addiert
(subtrahiert) oder auf beiden Seiten mit
(subtrahiert) oder
auf beiden
Seiten
mit derselben
von Null
derselben
von Null (dividiert).
verschiedenen
Zahl multipliziert (dividiert).
verschiedenen Zahl
multipliziert
Solche
Umformungen sind Äquivalenzumformungen.
Umformungen Solche
sind Äquivalenzumformungen.
Beispiel:
3x + (5x) + 3x = 3x + 25x + 3x = 28x + 3x
2
2
2
2
2
3x ⋅ 4x + 2x ⋅ 5x = 12x 2 + 10x 2 = 22x 2
b) Klammern auflösen:
Beispiele:
Plus vor der Klammer:
5 – 0,5x
5
2
1,6
L
=
=
=
=
=
3 + 0,75x
3 +1,25x
1,25x
x
{1,6}
L = {}
Grundwissen Mathematik
3x + (5x − 2y) = 3x + 5x − 2y = 8x − 2y
Minus vor der Klammer: x − (y2 − 2x) + y2 = x − y2 + 2x + y2 = x
falls G =
falls G =
7 – G8
Eine lineare Gleichung
hat Gleichung
entweder hat
genau
eine Zahl
keine
Eine lineare
entweder
keine,oder
genau
eine oder alle Zahlen der Grundmenge
Zahl (unerfüllbare
Gleichung)
oder
alle
Zahlen
der
Grundmenge
10
Daten
und
Diagramme
als Lösung.
(allgemeingültige
Gleichung)
als Lösung.
Das
arithmetische
Mittel (=Mittelwert) einer Datenreihe erhält
6. Mittelwert
man, wenn man alle Werte addiert und den Summenwert dann
Den
Mittelwert
(arithmetisches
Mittel) einer Datenreihe erhält man, wenn man alle Werte
durch
die Anzahl
der Werte dividiert.
addiert und den Summenwert dann durch die Anzahl der Werte dividiert.
Beispiel: Notenverteilung bei einer Mathematikschulaufgabe
Note
1
2
3
4
5
6
Anzahl
2
7
8
7
5
1
c) Multiplizieren von Summen (Ausmultiplizieren):
Allgemein: (a + b) ⋅ (c + d) = ac + ad + bc + bd
Beispiele:
(3x − 2y) ⋅ (4x − 10) = 12x 2 − 30x − 8xy + 20y
(1· 2 + 2· 7 + 3· 8 + 4 · 7 + 5· 5 + 6 · 1) : 30 = 3,3 (Mittelwert)
(a + b) ⋅ (a + b) = a 2 + ab + ba + b2 = a 2 + 2ab + b2
(m − n) ⋅ (m − n) = m 2 − mn − nm + n 2 = m 2 − 2mn + n 2
! + 0,5x
!-3
! : 1,25
Verschiedene Diagrammtypen zu obigem Beispiel:
7. Besondere Linien im Dreieck
Säulendiagramm
(2x + 3y) ⋅ (2x − 3y) = 4x 2 − 6xy + 6xy − 9y2 = 4x 2 − 9y2
Balkendiagramm
d) Faktorisieren (Ausklammern gemeinsamer Faktoren):
Beispiele:
−4a + 4b = −4 ⋅ (a − b)
ac + bc − ad − bd = c ⋅ (a + b) − d ⋅ (a + b) = (c − d) ⋅ (a + b)
Seite 11 von 12
Liniendiagramm
In jedem
Dreieck schneiden
sich die Seitenhalbierenden
sa, sb, sc in einem Punkt S.
Dieser Punkt S heißt
Schwerpunkt des Dreiecks.
Seite 12 von 12
Kreisdiagramm
In jedem
Dreieck schneiden
sich die Mittelsenkrechten
ma, mb, mc der Dreiecksseiten
in einem Punkt U, der von
den drei Ecken des Dreiecks
den gleichen Abstand hat.
U ist der Umkreismittelpunkt
des Dreiecks.
Die drei Winkelhalbierenden
wα, wβ, wγ eines Dreiecks
schneiden sich in einem
Punkt I, der von allen drei
Seiten des Dreiecks den
gleichen Abstand ϱ hat.
I ist der Inkreismittelpunkt
des Dreiecks.