2016_01_12, Geometrie, Flächeninhalt eines Trapezes

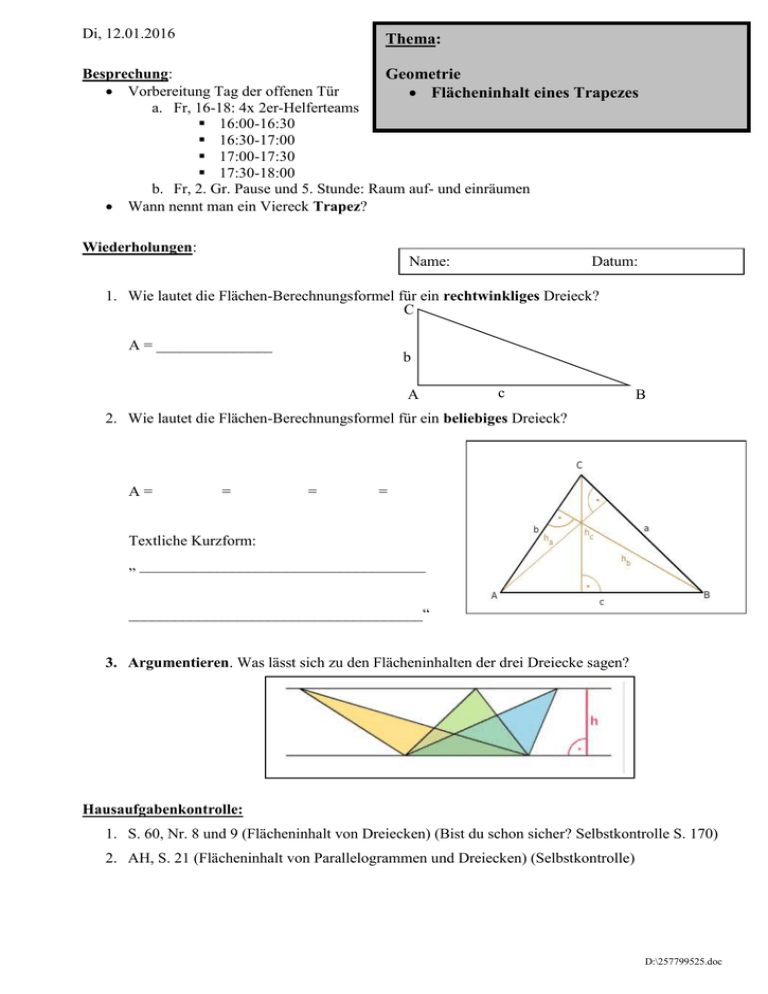
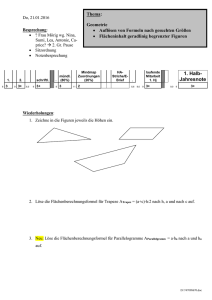
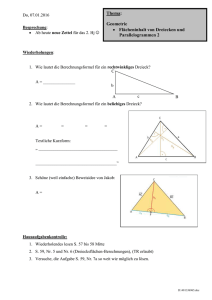
Di, 12.01.2016
Thema:
Besprechung:
Geometrie
 Vorbereitung Tag der offenen Tür
 Flächeninhalt eines Trapezes
a. Fr, 16-18: 4x 2er-Helferteams
 16:00-16:30
 16:30-17:00
 17:00-17:30
 17:30-18:00
b. Fr, 2. Gr. Pause und 5. Stunde: Raum auf- und einräumen
 Wann nennt man ein Viereck Trapez?
Wiederholungen:
Name:
Datum:
1. Wie lautet die Flächen-Berechnungsformel für ein rechtwinkliges Dreieck?
C
A = _______________
b
A
c
B
2. Wie lautet die Flächen-Berechnungsformel für ein beliebiges Dreieck?
A=
=
=
=
Textliche Kurzform:
„ _____________________________________
______________________________________“
3. Argumentieren. Was lässt sich zu den Flächeninhalten der drei Dreiecke sagen?
Hausaufgabenkontrolle:
1. S. 60, Nr. 8 und 9 (Flächeninhalt von Dreiecken) (Bist du schon sicher? Selbstkontrolle S. 170)
2. AH, S. 21 (Flächeninhalt von Parallelogrammen und Dreiecken) (Selbstkontrolle)
D:\257799525.doc
Thema: Flächeninhalt eines Trapezes
1. Wann nennt man Viereck Trapez?
2. Wie mag wohl die Höhe in einem Trapez definiert sein?
3. Bezeichnungen bei einem Trapez:
4. Leite aus der dir bekannten Flächen-Berechnungsformel für beliebige Dreiecke die
Flächenberechnungsformel A = ½ (a+c)h für Trapeze ab. Einen Beweis (eine Herleitung) dazu
findest du auf S. 124.
5. S. 125, Nr. 1 (Berechnungen)
a. A =
6. S. 125, Nr. 2b (Berechnungen im Koordinatensystem)
Hausaufgaben:
1. S. 125, Nr. 2c, 2d (Koordinatensystem), Nr. 4 (Tipp: Kästchenzählen)
2. Versuche bei Aufgabe 3c die Höhe h zu berechnen und eine Berechnungsformel anzugeben.
3. S. 125, Nr. 7 (einf. Flächenberechnungen bei Trapezen) (Bist du schon sicher? Selbstkontrolle)
4. S. 126, Nr. 13 (Textaufgabe, bei der Rechnung
müssen
die verwendeten
Formeln angegeben
Nr. 13 ist nicht
lösbar,
da die
Höhenangeben
fehlen.
werden, denke an den Antwortsatz und die richtigen Einheiten!)
D:\257799525.doc
Name:
Datum:
1. Wie lautet die Flächen-Berechnungsformel für ein rechtwinkliges Dreieck?
C
A = _______________
b
A
c
B
2. Wie lautet die Flächen-Berechnungsformel für ein beliebiges Dreieck?
A=
=
=
=
Textliche Kurzform:
„ _____________________________________“
3. Argumentieren. Was lässt sich zu den Flächeninhalten der drei Dreiecke sagen?
Name:
Datum:
1. Wie lautet die Flächen-Berechnungsformel für ein rechtwinkliges Dreieck?
C
A = _______________
b
A
c
B
2. Wie lautet die Flächen-Berechnungsformel für ein beliebiges Dreieck?
A=
=
=
=
Textliche Kurzform:
„ _____________________________________“
3. Argumentieren. Was lässt sich zu den Flächeninhalten der drei Dreiecke sagen?
D:\257799525.doc
Wiederholungen
1. Geldanlage bei der Bank für ein Jahr: Zinsen = 42,00 €, Zinssatz = 6%
a. Guthaben zu Beginn:
b. Guthaben nach 46 Tagen:
c. Guthaben nach 1 Jahr:
d. Guthaben nach 2 Jahren (Zinseszins):
e. Guthaben nach 3 Jahren (Zinseszins):
f. Guthaben nach n Jahren (Zinseszins):
2. Rechteck:
a. Umfangsformeln
b. Flächenberechnungsformel
3. Quader:
a. Volumenberechnungsformel
b. Oberflächenberechnungsformel
4. Parallelogramm
a. Umfangsformeln
b. Flächenberechnungsformel
c. Bestimme die fehlenden Größen des Parallelogramms
a
5 cm
b
2,5 cm
ha
2 cm
hb
A
8 cm
4 cm
7 cm
2,5 cm
5 cm
14 cm²
U
5. Winkel mit dem Geodreieck messen/zeichnen (Demo am Smartboard)
Zeichne den Winkel 120° in diesem Kasten.
D:\257799525.doc
6.
7. Welche beiden Haupteigenschaften hat ein Parallelgramm?
8. Beschriftung eines Parallelogramms (Eckpunkte, Winkel)
9. Definition der Höhen in einem Parallelogramm.
10. Rechtecke sind auch Parallelgramme. Wie sieht es dort mit den Höhen aus?
11. Einzeichnen der Höhen in einem Parallelogramm.
12. In welcher Beziehung stehen die 4 Winkel in einem Parallelogramm?
13. Was lässt sich zu den Flächeninhalten der drei Parallelogramme sagen? (Argumentieren)
D:\257799525.doc