2016_01_05, Geometrie, Flächeninhalt von Dreiecken 1

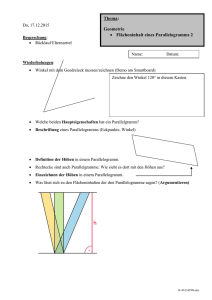
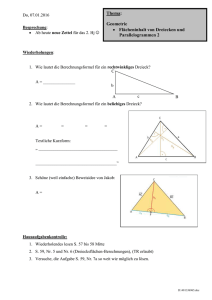
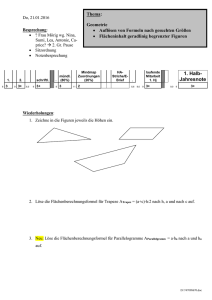
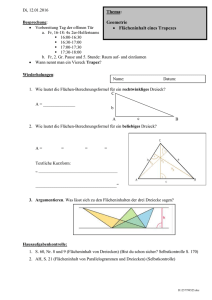
Thema:
Di, 05.01.2016
Geometrie
 Flächeninhalt von Dreiecken 1
Besprechung:

Name:
Datum:
Wiederholungen:
1. Beschriftung eines Parallelogramms (Eckpunkte, Winkel)
2. Neu: In welcher Beziehung stehen die 4 Winkel in einem Parallelogramm?
3. Definition der Höhen in einem Parallelogramm.
4. Einzeichnen der Höhen in einem Parallelogramm.
5. Wie berechnet man den Flächeninhalt eines Parallelogramms?
a
5 cm
b
2 cm
ha
3 cm
hb
A
8 cm
4 cm
7 cm
3 cm
5 cm
14 cm²
U
6. Was lässt sich zu den Flächeninhalten der drei Parallelogramme sagen? (Argumentieren)
Hausaufgabenkontrolle:
Sieh dir zur Wiederholung alles zum Thema Flächeninhalte von Parallelogrammen an.
D:\582641274.doc
Thema: Flächeninhalt von Dreicken 1
Name:
Datum:
1. Whg.: Beschrifte die drei Dreiecke (siehe 3.)
2. Die drei Höhen in einem Dreieck
Definition: In einem Dreieck ABC bezeichnet man das Lot vom Eckpunkt C auf
die gegenüberliegende Seite c als Höhe hc des Dreiecks zur Seite c. Entsprechend
werden die die Höhen hb, ha definiert.
3. Zeichen jeweils die drei Höhen ein.
A
A
A
4. Wenn du alle drei Höhen richtig eingetragen hast, fällt auf, dass _______________________
__________________________________________________________________________
5. Der Höhenschnittpunkt kann innerhalb, _____________________ und _________________
______________________________________________________________________ liegen.
6. Der Flächeninhalt eines rechtwinkligen Dreiecks.
A
7. Der Flächeninhalt eines (beliebigen) Dreiecks.
8. Berechne die Dreiecksflächen in Aufgabe Nr. 3.
D:\582641274.doc
Hausaufgaben:
1. Wiederholendes lesen S. 57 bis 58 Mitte
2. S. 59, Nr. 5 und Nr. 6 (Dreiecksflächen-Berechnungen), (TR erlaubt)
3. Versuche, die Aufgabe S. 59, Nr. 7a so weit wie möglich zu lösen.
D:\582641274.doc
Wiederholungen
1. Geldanlage bei der Bank für ein Jahr: Zinsen = 42,00 €, Zinssatz = 6%
a. Guthaben zu Beginn:
b. Guthaben nach 46 Tagen:
c. Guthaben nach 1 Jahr:
d. Guthaben nach 2 Jahren (Zinseszins):
e. Guthaben nach 3 Jahren (Zinseszins):
f. Guthaben nach n Jahren (Zinseszins):
2. Rechteck:
a. Umfangsformeln
b. Flächenberechnungsformel
3. Quader:
a. Volumenberechnungsformel
b. Oberflächenberechnungsformel
4. Parallelogramm
a. Umfangsformeln
b. Flächenberechnungsformel
c. Bestimme die fehlenden Größen des Parallelogramms
a
5 cm
b
2,5 cm
ha
2 cm
hb
A
8 cm
4 cm
7 cm
2,5 cm
5 cm
14 cm²
U
5. Winkel mit dem Geodreieck messen/zeichnen (Demo am Smartboard)
Zeichne den Winkel 120° in diesem Kasten.
D:\582641274.doc
6.
7. Welche beiden Haupteigenschaften hat ein Parallelgramm?
8. Beschriftung eines Parallelogramms (Eckpunkte, Winkel)
9. Definition der Höhen in einem Parallelogramm.
10. Rechtecke sind auch Parallelgramme. Wie sieht es dort mit den Höhen aus?
11. Einzeichnen der Höhen in einem Parallelogramm.
12. Was lässt sich zu den Flächeninhalten der drei Parallelogramme sagen? (Argumentieren)
D:\582641274.doc