2016_02_16, Rechnen mit Wahrscheinlichkeiten

Di, 16.02.2016
Thema:
Rechnen mit Wahrscheinlichkeiten
 Einfache Zufallsexperimente, Wahrscheinlichkeiten schätzen
und/oder berechnen
Besprechung:
1. Arbeit Nr. 3 nächste Wo Dienstag  Wiederholungszettel siehe unten, heute ohne Kopie
2. Das Zehntel
3. Sport am Donnerstag: BeachCenter!!!
Wiederholungen:
Zufallsexperiment: Befragen eines Schülers nach dem Wochentag, an dem er Geburtstag hat.
a. Ergebnismenge: S = {
b. P(
c. P (Mo, Di) =
d. Überprüfung der theoretischen Überlegungen anhand der Klassendaten.
Mo
Di
Mi
0,143
0,143
0,143
Do
Fr
Sa
So
0,143
0,143
0,143
Kontrolle
Abs. H
Rel. H.
WK, P
0,143
Hausaufgabenkontrolle:
1. S. 93, Nr. 1 (Münzwurf)
2. S. 93, Nr. 4, (12er-Würfel, Dodekaeder)
Bsp.: P(durch 3 teilbar) = P(3,6,9,12) = 4 von 12 =
4 1
 =0,333…. = 33,3… %
12 3
3. S. 94, Nr. 5, (Glücksräder)
D:\748898801.doc
Thema:
Tafel: Einfache Zufallsexperimente, Wahrscheinlichkeiten schätzen und/oder berechnen
1. Erkunden, S. 88, Einführungsaufgabe(n) oben. Bestimme (ohne wiederholtes Experimentieren)
jeweils P(6) und vergleiche. P(6) ist die Wahrscheinlichkeit dafür, dass eine 6 als Ergebnis
auftritt.
Zufallsexperiment: Glücksrad:
S={
PGlücksrad (6) =
Zufallsexperiment: besonderer Würfel:
S={
PWürfel (6)
=
Zufallsexperiment: Doppelwürfel:
S={
PDoppelwürfel (6) =
D:\748898801.doc
2. S. 90, Nr. 11 Zufallsexperiment Skatspiel, Ziehen einer Karte
S={
a. P(Herz) =
Vermutung für Anzahl bei einem zehnfachen Experiment: ______
Überprüfung:
b. P(Bildkarte) =
Vermutung für Anzahl bei einem zehnfachen Experiment: ______
Überprüfung:
c. P(Bube) =
d. P(Bube oder 7) =
e. P(nicht Dame) =
f. P(Pik) =
g. P(
D:\748898801.doc
3. Übung: S. 94, Nr. 7 (Kugeln ziehen)
a. S = {
P(weiß) =
b. S = {
P(gerade) =
4. Übung: S. 94, Nr. 6 („Buchstaben-Kugeln“ ziehen)
a. S =
b. P(„IN“) =
5. Übung: S. 94, Nr. 9 (Kugeln ziehen)
S={
a. P(rot) =
b. P(rot beim 2. Zug, nach weiß im ersten Zug) =
6. Übung: S. 94, Nr. 10 (Würfeln)
Übungen/Hausaufgaben:
1. S. 110, Nr. 2a (Roulette)
2. S. 115, Runde 1, Nr. 1, Nr. 2 (Selbstkontrolle, S. 179)
3. Bereite dich auf die Arbeit Nr. 3 vor.
D:\748898801.doc
Wiederholungen
1. Geldanlage bei der Bank für ein Jahr: Zinsen = 42,00 €, Zinssatz = 6%. Berechne:
a. Guthaben zu Beginn:
b. Guthaben nach 46 Tagen:
c. Guthaben nach 1 Jahr:
d. Guthaben nach 2 Jahren (Zinseszins):
e. Guthaben nach 3 Jahren (Zinseszins):
f. Guthaben nach n Jahren (Zinseszins):
2. Rechteck:
a. Umfangsformeln
b. Flächenberechnungsformel
3. Quader:
a. Volumenberechnungsformel
b. Oberflächenberechnungsformel
4. Parallelogramm
a. Umfangsformeln
b. Flächenberechnungsformel
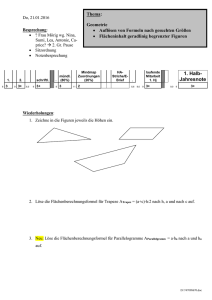
c. Bestimme die fehlenden Größen des Parallelogramms
a
5 cm
b
2,5 cm
ha
2 cm
hb
A
8 cm
4 cm
7 cm
2,5 cm
5 cm
14 cm²
U
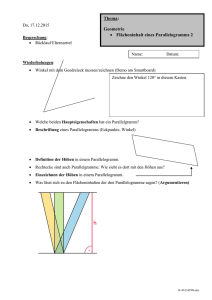
5. Winkel mit dem Geodreieck messen/zeichnen (Demo am Smartboard)
Zeichne den Winkel 120° in diesem Kasten.
D:\748898801.doc
6.
7. Welche beiden Haupteigenschaften hat ein Parallelgramm?
8. Beschriftung eines Parallelogramms (Eckpunkte, Winkel)
9. Definition der Höhen in einem Parallelogramm.
10. Rechtecke sind auch Parallelgramme. Wie sieht es dort mit den Höhen aus?
11. Einzeichnen der Höhen in einem Parallelogramm.
12. In welcher Beziehung stehen die 4 Winkel in einem Parallelogramm?
13. Was lässt sich zu den Flächeninhalten der drei Parallelogramme sagen? (Argumentieren)
14. Wann nennt man ein Viereck Trapez?
15. Wie lautet die Flächen-Berechnungsformel für Parallelogramme? A = ___________________
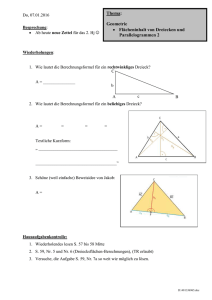
16. Wie lautet die Flächen-Berechnungsformel für ein rechtwinkliges Dreieck?
C
A = _______________
b
A
c
B
D:\748898801.doc
17. Wie lautet die Flächen-Berechnungsformel für ein beliebiges Dreieck?
A=
=
=
=
Textliche Kurzform:
„ _____________________________________
______________________________________“
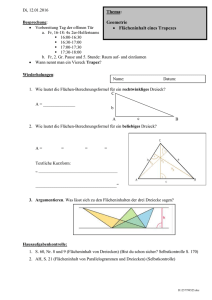
18. Argumentieren. Was lässt sich zu den Flächeninhalten der drei Dreiecke sagen?
19. Wie lautet die Flächen-Berechnungsformel für ein Trapez? A = _______________________
20. Zeichne in die Figuren jeweils alle Höhen ein.
D:\748898801.doc
21. Löse die Flächenberechnungsformel für Trapeze ATrapez = (a+c)∙h:2 nach h, a und nach c auf.
22. Löse die Flächenberechnungsformel für Parallelogramme AParallelgramm = a∙ha nach a und ha auf.
23. Löse die Flächenberechnungsformel für beliebige Dreicke ADreieck = a∙ha:2 nach a und ha auf.
24. Löse m = (a+c):2 nach a auf.
25. Löse AT = (a+c)∙h:2 nach a auf.
26. Berechne a für AT = 20cm², c = 6cm, h = 2cm
27.
A1 =
D:\748898801.doc
A4 =
28. Welches sind die Haupteigenschaften eines Prismas?
29. Entscheide, ob die folgenden Körper Prismen sind.
30. Wie lautet die Volumen-Berechnungsformel für Prismen?
31. Wie lautet die Volumen-Berechnungsformel für Prismen mit rechtwinkligem Dreieck als
Grundfläche?
32. Wie lautet die Volumen-Berechnungsformel für Prismen mit Parallelogramm als Grundfläche?
33. Bei einem Prisma ist die Form der Grundfläche nicht bekannt. Man weiß aber, dass die
Grundfläche 14cm² groß ist und die Höhe des Prismas 14cm beträgt. Kann man das Volumen
des Prismas berechnen?
34. Wie berechnet man die Fläche eines beliebigen Vielecks?
D:\748898801.doc
35. Was versteht man bei einem Prisma unter einem Mantel und wie wird er berechnet?
36. Wie lautet die Oberflächen-Berechnungsformel für Prismen?
Löse die Oberflächen-Berechnungsformel für Prismen nach M auf.
37. Das Volumen eines Quaders mit der Kantenlänge a = 2cm und der Höhe h = 5dm beträgt V =
500cm³. Berechne den Oberflächeninhalt des Quaders. (Buch S. 138, Nr. 9)
38. S. 138, Nr. 10
Bei einem Haus mit Hanglage wird die Baugrube nicht quaderförmig ausgehoben, sondern so,
dass die Betonplatte waagerecht verläuft.
a. Gib die notwendige Volumenberechnungsformel an.
b. Berechne, wie viele Kubikmeter Erde für die Baugrube ausgebaggert werden müssen.
39.
D:\748898801.doc