Mo, 07

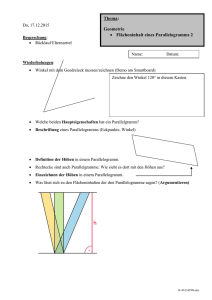
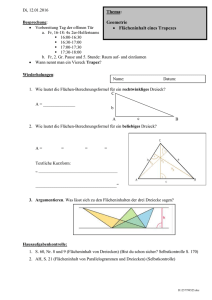
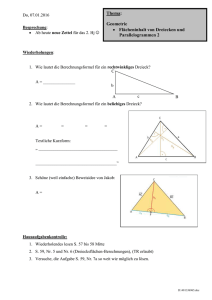
Thema:
Do, 21.01.2016
Geometrie
 Auflösen von Formeln nach gesuchten Größen
 Flächeninhalt geradlinig begrenzter Figuren
Besprechung:
 ? Frau Mörig wg. Nina,
Sumi, Lea, Antonie, Caprice?  2. Gr. Pause
 Sitzordnung
 Notenbesprechung
1.
8
3
2.
9
3+
Mindmap
Zuordnungen
(20%)
mündl.
schriftl. . . (80%)
8,5
9
3+
8
3
11
HAStriche/EBrief
2
laufende
Mitarbeit
1. Hj
.
.
8,6
8,6
9
3+
1. HalbJahresnote
9,0
9
3+
Wiederholungen:
1. Zeichne in die Figuren jeweils die Höhen ein.
2. Löse die Flächenberechnungsformel für Trapeze ATrapez = (a+c)∙h:2 nach h, a und nach c auf.
3. Neu: Löse die Flächenberechnungsformel für Parallelogramme AParallelgramm = a∙ha nach a und ha
auf.
D:\747098670.doc
4. Neu: Löse die Flächenberechnungsformel für beliebige Dreicke ADreieck = a∙ha:2 nach a und ha
auf.
Übung: S. 125, Nr. 3 (fehlende Größen bei Trapezen berechnen)
D:\747098670.doc
Hausaufgabenkontrolle:
1. S. 125, Nr. 4 (alt)
2. S. 126, Nr. 15a (Textaufgabe, bei der Rechnung müssen die verwendeten Formeln angegeben
werden, denke an den Antwortsatz und die richtigen Einheiten!)
3. S. 127, Nr. 20, 21 (Kannst du noch Gleichungen lösen? Selbstkontrolle auf S. 181)
4. AB Zweiter Beweis der Berechnungsformel für Trapeze A = ½ (a+c)h
Ausgang ist der Text auf S. 124 oben. Ein Trapez wird doppelt ausgeschnitten.
5. Lies S. 130 und S. 131 oben. Du musst deinen Mitschülern jeweils an einem Beispiel die
Zerlegungs- bzw. die Ergänzungsmethode erklären können.
Thema: Flächeninhalt geradling begrenzter Figuren
1. Was ist eine geradlinig begrenzte Figur?
2. S. 130, oben, Einstiegsaufgabe „Haus verklinkern“.
3. Lies S. 130 und S. 131 oben. Du musst deinen Mitschülern jeweils an einem Beispiel die
Zerlegungs- bzw. die Ergänzungsmethode erklären können
Übungen/Hausaufgaben:
1. S. 131, Nr. 1, 2a, 2e, 2f, 3b, 4
2. Reste von S. 125, Nr. 3
D:\747098670.doc
Wiederholungen
1. Geldanlage bei der Bank für ein Jahr: Zinsen = 42,00 €, Zinssatz = 6%
a. Guthaben zu Beginn:
b. Guthaben nach 46 Tagen:
c. Guthaben nach 1 Jahr:
d. Guthaben nach 2 Jahren (Zinseszins):
e. Guthaben nach 3 Jahren (Zinseszins):
f. Guthaben nach n Jahren (Zinseszins):
2. Rechteck:
a. Umfangsformeln
b. Flächenberechnungsformel
3. Quader:
a. Volumenberechnungsformel
b. Oberflächenberechnungsformel
4. Parallelogramm
a. Umfangsformeln
b. Flächenberechnungsformel
c. Bestimme die fehlenden Größen des Parallelogramms
a
5 cm
b
2,5 cm
ha
2 cm
hb
A
8 cm
4 cm
7 cm
2,5 cm
5 cm
14 cm²
U
5. Winkel mit dem Geodreieck messen/zeichnen (Demo am Smartboard)
Zeichne den Winkel 120° in diesem Kasten.
D:\747098670.doc
6.
7. Welche beiden Haupteigenschaften hat ein Parallelgramm?
8. Beschriftung eines Parallelogramms (Eckpunkte, Winkel)
9. Definition der Höhen in einem Parallelogramm.
10. Rechtecke sind auch Parallelgramme. Wie sieht es dort mit den Höhen aus?
11. Einzeichnen der Höhen in einem Parallelogramm.
12. In welcher Beziehung stehen die 4 Winkel in einem Parallelogramm?
13. Was lässt sich zu den Flächeninhalten der drei Parallelogramme sagen? (Argumentieren)
14. Wann nennt man ein Viereck Trapez?
15. Wie lautet die Flächen-Berechnungsformel für Parallelogramme? A = ___________________
16. Wie lautet die Flächen-Berechnungsformel für ein rechtwinkliges Dreieck?
C
b
D:\747098670.doc
A = _______________
17. Wie lautet die Flächen-Berechnungsformel für ein beliebiges Dreieck?
A=
=
=
=
Textliche Kurzform:
„ _____________________________________
______________________________________“
18. Argumentieren. Was lässt sich zu den Flächeninhalten der drei Dreiecke sagen?
19. Wie lautet die Flächen-Berechnungsformel für ein Trapez? A = _______________________
20.
D:\747098670.doc