Einführung in die Elektrotechnik für Medienwissenschaftler

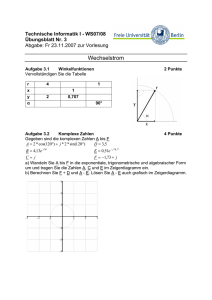
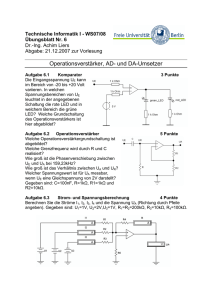
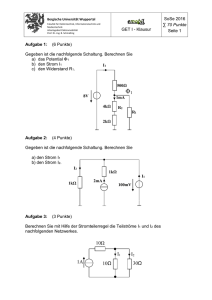
Einführung in die Elektrotechnik für Medienwissenschaftler
Elektrotechnische Grundlagen der Technischen Informatik
Übungsblatt 4
Aufgabe 1: Die Ausgangsstufe eines logischen Schaltkreises kann vereinfacht durch den gestrichelt
umrandeten Schaltungsteil im obigen Netzwerk dargestellt werden. Der Schalter S
repräsentiert in Stellung 1 eine logische Null und in Stellung 2 eine logische Eins.
An den Klemmen a und b ist eine Induktivität L und ein Widerstand R3 angeschlossen.
Der Schalter S befindet sich seit sehr langer Zeit in Stellung 1, so daß sich ein eingeschwungener Zustand eingestellt hat.
R1
a
2
1
L
iL (t)
S
U0 = 5V
R1 = 1kΩ
U0
R2
R3
u1 (t)
R2 = 1kΩ
R3 = 4kΩ
L = 0.5H
b
Netzwerk
Zum Zeitpunkt t = 0 wird der Schalter S in Stellung 2 gebracht.
a) Wie groß ist der Strom iL (t = 0) unmittelbar nach dem Umschalten des Schalters?
b) Zeichnen Sie das LAPLACE-Ersatzschaltbild der gesamten Schaltung für die
Zeiten t ≥ 0.
c) Berechnen Sie U 1 (s), die LAPLACE-Transformierte von u1 (t).
d) Berechnen Sie u1 (t) als invers LAPLACE-Transformierte von U 1 (s).
Nachdem sich der Schalter S sehr lange Zeit in Stellung 2 befunden hat (eingeschwungener Zustand), wird er zum Zeitpunkt t=T wieder in Stellung 1 gebracht.
e) Wie groß ist der Strom iL (t = T ) unmittelbar nach dem Umschalten des Schalters S?
1
f) Zeichnen Sie das LAPLACE-Ersatzschaltbild der gesamten Schaltung für die
Zeiten t ≥ T .
g) Berechnen Sie (für die Zeiten t ≥ T ) U 1 (s), die LAPLACE-Transformierte von
u1 (t).
h) Berechnen Sie (für die Zeiten t ≥ T ) u1 (t) als invers LAPLACE-Transformierte
von U 1 (s).
i) Zeichen Sie den Verlauf der Spannung u1 (t) für Zeiten t ≥ 0 unter Angabe charakteristischer Amplituden- und Zeitwerte.
2
Aufgabe 2: Zur Messung der Größen eines unbekannten RL-Gliedes wird folgende Schaltung aufgebaut:
Ri
2
1
S
U0 = 6V
U0
u(t)
R
L
Ri = 10Ω
Netzwerk
Beim Umschalten des Schalters von Stellung 1 nach Stellung 2 zum Zeitpunkt t = 0 (das
System befindet sich vor dem Umschalten in Ruhe) wird der Verlauf der Spannung u(t)
mit einem Oszilloskop aufgezeichnet und es werden die unten im Bild 1 angegebenen
Werte gemessen.
u(t) in V
4
3
2
1
0
0
0.9
1.8
2.7
Bild 1
3.6
4.5
t in ms
a) Zeichnen Sie das vollständige LAPLACE-Ersatzschaltbild der Schaltung für Zeiten
t ≥ 0.
b) Bestimmen Sie die LAPLACE-Transformierte U (s) der Spannung u(t) für t ≥ 0.
c) Bestimmen Sie die u(t) als invers LAPLACE-Transformierte von U (s).
d) Bestimmen Sie die Größen der Bauelemente R und L allgemein und zahlenmäßig.
3
Aufgabe 3: Gegeben ist die unten dargestellte Schaltung, bestehend aus der Gleichspannungsquelle
U0 , den Widerständen R1 , R2 , der Kapazität C und dem Schalter S. Der Schalter S ist
seit sehr langer Zeit geöffnet; zum Zeitpunkt t = 0 wird er geschlossen.
R1
S
U0 = 20V
ic (t)
U0
uc (t)
C
R1 = 2kΩ
R2
R2 = 2kΩ
C = 1µF
Netzwerk
a) Wie groß ist die Spannung uc (t = 0) unmittelbar nach dem Schließen des Schalters
S?
b) Zeichnen Sie das LAPLACE-Ersatzschaltbild der gegebenen Schaltung für Zeiten
t ≥ 0.
c) Berechnen Sie U c (s) (die LAPLACE-Transformierte von uc (t) ).
d) Berechnen Sie uc (t) als invers LAPLACE-Transformierte von U c (s).
e) Berechnen Sie den Strom ic (t).
f) Skizzieren Sie die Verläufe des Stromes ic (t) und der Spannung uc (t) unter Angabe
charakteristischer Werte.
4
replacemen
10+10*exp(-1000*x)
20
uc (t) in V
18
16
14
12
10
0
0.001
0.002
0.003
0.004
0.005
0.006
0.007
t in s
uc (t) zu (f)
0
-0.01*exp(-1000*x)
ic (t) in A
-0.002
-0.004
-0.006
-0.008
-0.01
0
0.001
0.002
0.003
ic (t) zu (f)
5
0.004
0.005
0.006
0.007
t in s