Protokoll 03 (harald)

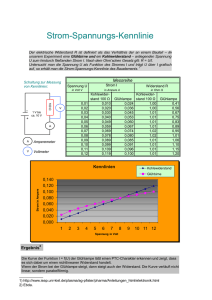
Versuch Nr. 03: Widerstandsmessung mit der Wheatstone-Brücke
Versuchsdurchführung: Donnerstag, 28. Mai 2009 von Sven Köppel / Harald Meixner
Protokollant: Harald Meixner
Tutor: Batu Klump
Inhalt
1. Aufgabenstellung und physikalischer Hintergrund
1.1. Was ist ein elektrischer Widerstand?
1.2. Aufgabenstellung
2. Messmethode und Schaltbilder
3. Messergebnisse
3.1. Drahtwiderstand
3.2. Platin-Präzisionswiderstand
3.3. Thermistor
4. Bestimmung des Temperaturkoeffizienten
5. Herleitung der Abgleichbedingung
6. Fehlerbetrachtung
6.1. Genauigkeit der Wheatstoneschen Brücke
6.2. Wann wird der Fehler von R minimal?
7. Wheatstonebrücke als Thermometer
1. Aufgabenstellung und physikalischer Hintergrund
1.1. Was ist ein elektrischer Widerstand?
Elektrischer Strom besteht aus relativ frei beweglichen Elektronen, die sich durch einen Leiter
bewegen. Je mehr Elektronen fließen, desto größer ist die Stromstärke. Da sich beim Fließen eines
Stroms immer sehr viele Elektronen bewegen, führen sie viele elastische Stöße dabei aus, sowohl
mit anderen Elektronen als auch mit bestimmten atomaren Bestandteilen des Leitermaterials. Durch
diese Stoßprozesse wird die eigentlich gerichtete Bewegung gestreut und behindert. Die Elektronen
müssen nun eine bestimmte elektrische Energie besitzen (=Spannung) um gegen diese
„Behinderung“, also den elektrischen Widerstand, anzukommen.
Will man also einen bestimmten elektrischen Strom durch einen Leiter fließen lassen, so ist der
elektrische Widerstand ein Maß dafür, wie viel elektrische Spannung man dafür benötigt.
1.2. Aufgabenstellung
In diesem Versuch werden nun folgende Aufgaben durchgeführt:
1. Die Abhängigkeit von der Temperatur wird bei 3 unterschiedlichen Widerständen im
Bereich von 20°C bis 100°C gemessen und graphisch dargestellt.
2. Der Temperaturkoefffizient β, definiert durch die Gleichung
R= R0∗1 βθ
3.
4.
5.
6.
7.
wobei R0 der Widerstand bei 0°C und θ die Temperatur in Grad Celsius ist.
Die Abgleichbedingung wird hergeleitet.
Fehlerbetrachtung
Die Messunsicherheit der Wheatstonebrücke wird mit der Messunsicherheit verglichen, die
sich ergibt, wenn man den Widerstand aus dem ohmschen Gesetz durch I und U errechnet.
Die Wheatstonebrücke soll als Thermometer verwendet werden.
Es wird untersucht, wie man die Widerstände in Aufgabe 6 dimensionieren muss, um eine
möglichst optimale Linearität zu erhalten.
2. Messmethode und Schaltbilder
Zur Bestimmung wird die sogenannte Wheatstonesche Brücke verwendet. Das Prinzipschaltbild der
Wheatstonschen Brücke ist unter Schaltbild 1 dargestellt. Das Voltmeter im Zentrum der Schaltung
bezeichnet man als Nullinstrument. Es zeigt unabhängig von der angelegten Spannung keinen
Ausschlag, wenn
R 1 R3
=
R 2 R4
gilt. Dies ist die sogenannte Abgleichbedingung. Setzt man nun für einen der bekannten
Widerstanden einen unbekannten Widerstand R x ein und hat man die Möglichkeit, einen der
bekannten Widerstände zu variieren, so kann man R x bestimmen, indem man durch variieren des
veränderbaren Widerstandes dafür sorgt, dass das Nullinstrument keinen Ausschlag mehr anzeigt
(„Brückenabgleich“). Nun braucht man die Abgleichbedingung nur noch nach R x auflösen und
hat damit den Widerstand bestimmt.
In durchgeführten Experiment wurden die Widerstände R1 und R2 durch einen ausgespannten
Draht ersetzt, auf dem sich ein Schleifkontakt bewegt (dargestellt in Schaltbild2). Anstelle der
Widerstandswerte geht nun also das Verhältnis der Längen der Drahtabschnitte, bezeichnet mit
a
in die Abgleichbedingung ein. Mithilfe des Schleifkontakts kann man nun den
b
Brückenabgleich herbeiführen. Der unbekannte Widerstand R x berechnet sich nun aus dem
Produkt des bekannten Widerstands mit dem Verhältnis der Drahtabschnitte:
a
R x =Rn
(Herleitung folgt in 5.)
b
Als bekannten Widerstand Rn wird ein Stöpselwiderstand verwendet. Dieser besteht aus
mehreren in Reihe geschalteten Präzisionswiderständen von unterschiedlicher Größe, welche man
gezielt zuschalten und überbrücken kann, um unterschiedliche Gesamtwerte für den Widerstand zu
erhalten.
Schaltbilder
Prinzipieller Aufbau der Wheatstoneschen Brücke:
Schaltbild1
Praktische Ausführung im Versuch:
Schaltbild2
3. Messergebnisse
3. 1. Für den Drahtwiderstand wurden folgende Werte gemessen:
Temp [°C]
22,5
36
42
48,6
54,7
59,9
65,9
72,1
79,4
94
a [cm]
23,7
23,6
23,2
23,1
23,05
22,95
22,85
22,1
22,1
22,1
b [cm]
76,3
76,4
76,8
76,9
76,95
77,05
77,15
77,9
77,9
77,9
Rn [Ohm]
100
100
100
100
100
100
100
100
100
100
Rx [Ohm]
31,06
30,89
30,21
30,04
29,95
29,79
29,62
28,37
28,37
28,37
Δ Temp [°C]
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
Δ Rx
0,79
0,79
0,77
0,77
0,77
0,76
0,76
0,73
0,73
0,73
Graphische Darstellung:
40
Anfängerpraktikum 2
Versuch 3, Aufgabe 1
Drahtwiderstand
38
Linear Regression for DRAHTWIDERSTA_RX:
Y=A+B*X
Parameter
Value Error
-----------------------------------------------------------A
32,21586
0,32464
B
-0,04433
0,00532
------------------------------------------------------------
36
34
R
32
30
28
26
24
22
20
10
20
30
40
50
60
70
80
90
100
Temp
Der Widerstandswert schwankt im Bereich zwischen 20°C und 100°C nur um ungefähr 3Ω. In
kleinen Temperaturbereichen kann der Drahtwiderstand also als konstant angenommen werden.
3. 2. Für den Platin-Präzisionswiderstand ergaben sich folgende Messwerte:
Temp [°C]
26,6
33,7
39,7
48
55,4
63,8
71,7
82,3
86,7
92,5
a [cm]
54
54,3
54,9
55,35
55,9
56,4
56,8
57,3
57,65
58
b [cm]
46
45,7
45,1
44,65
44,1
43,6
43,2
42,7
42,35
42
Rn [Ohm]
100
100
100
100
100
100
100
100
100
100
Rx [Ohm]
117,39
118,82
121,73
123,96
126,76
129,36
131,48
134,19
136,13
138,1
Δ Temp [°C]
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
Δ Rx
1,26
2,86
2,93
2,98
3,05
3,11
3,17
3,23
3,28
3,33
Graphische Darstellung:
Anfängerpraktikum 2
Versuch 3, Aufgabe 1
Platin-Präzisionswiderstand
R / Ohm
140
Linear Regression for PLATINPRÄZIS_RX:
Y=A+B*X
120
Parameter
Value Error
-----------------------------------------------------------A
108,95769
0,37172
B
0,31369
0,00582
------------------------------------------------------------
20
30
40
50
60
70
80
90
100
t / Cel
Der Platin-Präzisionswiderstand zeigt eine sehr lineare Abhängigkeit von der Temperatur.
3. 3. Messergebnisse für den Thermistor aus Halbleitermaterial:
Temp [°C]
94,7
82,3
73,4
64,6
56,1
49,6
44,3
39,4
34,4
27,6
a [cm]
34,2
40,8
45,7
50
54,7
58,6
62
43,5
46,4
50,1
b [cm]
65,8
59,2
54,3
50
45,3
41,4
38
56,5
53,6
49,9
Rn [Ohm]
100
100
100
100
100
100
100
300
300
300
Rx [Ohm]
51,98
68,92
84,16
100
120,75
141,55
163,16
230,97
259,7
301,2
Δ Temp [°C]
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
Δ Rx
1,27
1,66
2,02
2,4
2,9
3,41
3,96
5,56
6,24
7,23
Graphische Darstellung:
Anfängerpraktikum 2
Versuch 3, Aufgabe 1
Thermistor aus Halbleitermaterial
350
300
Data: Thermistor_Rx
Model: ExpDec1
Equation: y = A1*exp(-x/t1) + y0
Weighting:
y
Instrumental
R / Ohm
250
Chi^2/DoF
= 7.84615
R^2
= 0.98622
200
y0
A1
t1
150
34.45074
813.78864
25.41327
±2.86449
±42.9654
±1.04864
100
50
20
30
40
50
60
70
80
90
100
t / Cel
Der Thermistor zeigt eine exponentielle Temperaturabhängigkeit. Dies ist ein deutliches Zeichen
dafür, dass es sich hier nicht um einen Ohmschen Widerstand handelt.
4. Bestimmung des Temperaturkoeffizienten
Der Temperaturkoeffizient ist definiert über
R= R0 1 βθ 
β berechnet sich also über
β=
R−R0
θR0
Man benötigt zur Bestimmung von β den Widerstand bei 0°C. Diesen kann man aus den linearen
Regressionen der graphischen Darstellungen entnehmen.
Bei den Widerständen, die einen linearen Verlauf zeigen, gibt es außerdem einen Zusammenhang
zwischen der Steigung der Geraden und dem Temperaturkoeffizienten:
Die Steigung der Regressionsgeraden ist einfach:
a=
R− R0
θ
und damit lässt β sich nun berechnen durch
β=
a
R0
Es ergeben sich nun folgende Temperaturkoeffizienten:
Widerstand
Drahtwiderstand
Platin-Präzisionswiderstand
R bei 0° [Ohm] Steigung a
32,21
0,044
108,95
0,313
Temperaturkoeffizient
0,00137
0,00287
Für den Thermistor lässt sich keine lineare Regression durchführen.
Der maximale Fehler ließe sich nun Berechnen durch:
Δβ =
Δa a
 ΔR0
R 0 R20
Schaut man sich einmal den zweiten Term dieser Gleichung an, so sieht man leicht, dass dieser
Fehler extrem klein sein wird.
5. Herleitung der Abgleichbedingung
Für die Herleitung der Abgleichbedingung schaut man sich Schaltbild 2 an. Es seien nun
Ux
Un
Ua
Ub
= An Widerstand R x abfallende Spannung
= An Widerstand Rn abfallende Spannung
= An Drahtabschnitt a ( = Ra ) abfallende Spannung
= An Drahtabschnitt b (= Rb ) abfallende Spannung
Geht man zunächst davon aus, dass alle Widerstände gleich sind, so ergibt sich für die
entsprechenden Ströme:
U x =U a ⇒ R x∗I 2=Ra∗I 2
U n=U b ⇒ R n∗I 1=Rb∗I 1
Diese Gleichungen lassen sich nun so umstellen, dass die Ströme nicht mehr in Ihnen auftauchen:
R x Ra
=
R n Rb
Die Widerstände Ra und Rb standen für den durch die Drahtabschnitte a und b verursachten
Widerstände. Da es nur auf das Verhältnis der Widerstände zueinander ankommt, können wir sie
nun in der Gleichung die Längen a und b ersetzen. Nun braucht man nur noch nach R x
aufzulösen und erhält die Abgleichbedingung:
R x =Rn
a
b
6. Fehlerbetrachtungen
6. 1. Genauigkeit der Wheatstonebrücke
Der Fehler von R x lässt sich berechnen durch
ΔR x =ΔR n
a
l
R n
Δa
2
l −a
l−a
(1)
Um nun die Messunsicherheit bei der Wheatstonebrücke mit der Messunsicherheit bei Bestimmung
des Widerstandes mithilfe des Ohmschen Gesetzes zu vergleichen schauen wir nun exemplarisch
auf den Drahtwiderstand. Aus der unter Messergebnisse angegebenen Tabelle kann man entnehmen,
dass der durchschnittliche Fehler von R etwa 0,76 Ohm entspricht. Der Drahtwiderstand war
während der Messung relativ konstant. Gehen wir nun davon aus dass der Widerstand im Mittel
29,6 Ohm groß war, so ergibt sich ein Fehler pro Ohm von ungefähr 2%.
Würde man den Widerstand bestimmen, indem man Spannung und Stromstärke mit Geräten mit je
1,5% Fehler misst, so erhält man einen maximalen Fehler von 3% pro Ohm. Die Wheatstonebrücke
ist also genauer.
6. 2. Wann wird der Fehler von R x minimal?
Ausgangsformel ist nochmal (1). Zur Vereinfachung der folgenden Rechnung nehmen wir nun an,
der Fehler des Vergleichswiderstandes Rn sei vernachlässigbar klein, sodass für den Fehler nun
gilt:
ΔR x =Rn
l
Δa
l−a2
Der Fehler ist nun also eine Funktion die von Rn und a abhängt, da sowohl l als auch der Fehler
von a konstant sind. Diese Funktion muss nun also minimal werden. Löst man die
Abgleichbedingung nach a auf und setzt ein, so kann man a aus der Gleichung elminieren und
erhält:
2
 Rn R x 
ΔR x =
l −Rn
Leiten wir nun partiell nach Rn ab, so ergibt die Nullstelle, dass das Minimum des Fehler bei
Rn = R x . Der Fehler wird also am kleinsten, wenn der Vergleichswiderstand möglichst so
groß ist, wie der zu messende Widerstand.
7. Wheatstonesche Brücke als Thermometer
Wie die Messergebnisse zeigen, hat der Platin-Präsizionswiderstand eine sehr lineare Abhängigkeit
von der Temperatur. Gleicht man mit diesem Widerstand also die Brücke bei einer bestimmten
Temperatur so an, dass das Nullinstrument nichts mehr anzeigt, so lässt sich anschließend jede
Temperaturänderung mit einem Ausschlag des Instruments registrieren. Da die Abhängigkeit des
Widerstands linear ist, ist auch der Ausschlag des Instruments linear und man kann die
Wheatsonebrücke als Thermometer nutzen.
Im Versuch wurde die Wheatstonebrücke bei 60° angeglichen und dann die Temperatur variiert. Es
wurden folgende Ergebnisse gemessen:
Temp [°C]
40
45
50
60
73
80
90
U [mv]
32
24
12
0
-24
-36
-52
Δ Temp [°C]
0,1
0,1
0,1
0,1
0,1
0,1
0,1
Δ U [mv]
0,64
0,48
0,24
0
-0,48
-0,72
-1,04
Graphische Darstellung:
90
Temperatur C°
80
70
60
50
40
-60
-40
-20
0
20
40
Spannung mV
Eine Variation des Messgerätes von „empfindlich“ und „unempfindlich“ brachte bei den
Messwerten keine ablesbaren Änderungen.
Man erkennt gut die lineare Abhängigkeit im Bereich zwischen 60° und 90°. Im Bereich zwischen
50° und 60° allerdings ist ein deutliches Abweichen der Linearität festzustellen. Schaut man sich
allerdings die Tabelle mit den Messergebnissen an, so beruht dieses Abweichen von der Linearität
nur auf einem einzigen Messwert und ist vermutlich die Folge eines Ablesefehlers.
Auch hier ist es ideal, wenn die verwendeten Widerstände etwa dieselbe Größe haben, damit der
Fehler am geringsten und somit die Linearität am besten wird.