Ausführliche Anleitung

Grundlagen der Elektrotechnik
1
Übungsaufgaben zur Wechselstromtechnik mit Lösung
Aufgabe 1
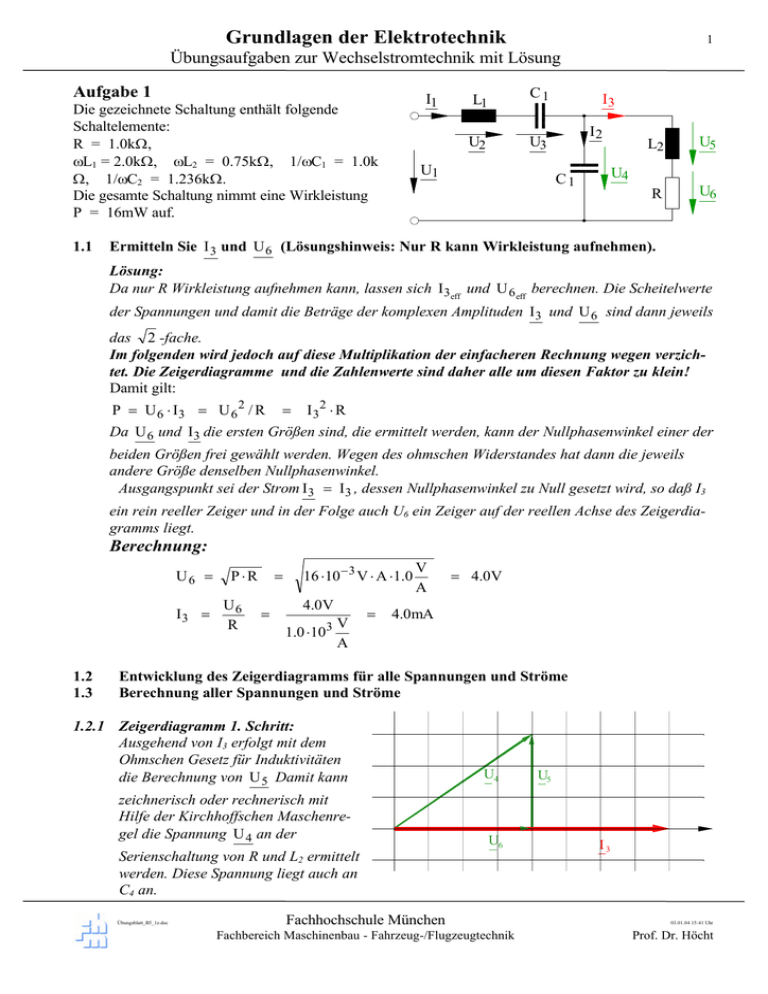
I1
Die gezeichnete Schaltung enthält folgende
Schaltelemente:
R = 1.0kΩ,
ωL1 = 2.0kΩ, ωL2 = 0.75kΩ, 1/ωC1 = 1.0k
Ω, 1/ωC2 = 1.236kΩ.
Die gesamte Schaltung nimmt eine Wirkleistung
P = 16mW auf.
1.1
L1
C1
U2
U3
U1
I3
I2
L2
U5
R
U6
U4
C1
Ermitteln Sie I 3 und U 6 (Lösungshinweis: Nur R kann Wirkleistung aufnehmen).
Lösung:
Da nur R Wirkleistung aufnehmen kann, lassen sich I3eff und U 6 eff berechnen. Die Scheitelwerte
der Spannungen und damit die Beträge der komplexen Amplituden I3 und U 6 sind dann jeweils
das 2 -fache.
Im folgenden wird jedoch auf diese Multiplikation der einfacheren Rechnung wegen verzichtet. Die Zeigerdiagramme und die Zahlenwerte sind daher alle um diesen Faktor zu klein!
Damit gilt:
P = U 6 ⋅ I3 = U 6 2 / R = I 32 ⋅ R
Da U 6 und I3 die ersten Größen sind, die ermittelt werden, kann der Nullphasenwinkel einer der
beiden Größen frei gewählt werden. Wegen des ohmschen Widerstandes hat dann die jeweils
andere Größe denselben Nullphasenwinkel.
Ausgangspunkt sei der Strom I3 = I3 , dessen Nullphasenwinkel zu Null gesetzt wird, so daß I3
ein rein reeller Zeiger und in der Folge auch U6 ein Zeiger auf der reellen Achse des Zeigerdiagramms liegt.
Berechnung:
U6 =
I3 =
1.2
1.3
P⋅R
U6
R
=
=
16 ⋅10 − 3 V ⋅ A ⋅1.0
4.0V
1.0 ⋅103
V
A
=
V
A
= 4.0V
4.0mA
Entwicklung des Zeigerdiagramms für alle Spannungen und Ströme
Berechnung aller Spannungen und Ströme
1.2.1 Zeigerdiagramm 1. Schritt:
Ausgehend von I3 erfolgt mit dem
Ohmschen Gesetz für Induktivitäten
die Berechnung von U 5 Damit kann
U
_4
zeichnerisch oder rechnerisch mit
Hilfe der Kirchhoffschen Maschenregel die Spannung U 4 an der
U
_6
Serienschaltung von R und L2 ermittelt
werden. Diese Spannung liegt auch an
C4 an.
Übungsblatt_B5_1z.doc
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
U
_5
_I 3
03.01.04 15:41 Uhr
Prof. Dr. Höcht
Grundlagen der Elektrotechnik
2
Übungsaufgaben zur Wechselstromtechnik mit Lösung
Berechnung mit Hilfe des Zeigerdiagramms
U 5 = U 5 = R ⋅ I3 = 1.0kΩ ⋅ 4.0mA = 4.0V
Wegen des ohmschen Widerstands haben I3 und U6 gleiche Phasenlage.
U 5 = U 5 = ωL 2 ⋅ I3 = 0.75kΩ ⋅ 4.0mA = 3.0V
Da bei der Induktivität die Spannung um 90° vorauseilt, steht dieser Zeiger nach oben.
U 4 = U5 + U 6
Die Maschenregel liefert:
Die Länge U4 des Zeigers U 4 , also der Betrag U 4 = U 4 ergibt sich mit Hilfe des Satzes von
Pythagoras zu
U4 =
U 52 + U 6 2 =
4.0 2 + 3.0 2 V = 5.0V
Berechnung mit Hilfe der komplexen Darstellung:
Da als Ausgangspunkt der gesamten Darstellung der Nullphasenwinkel des Stroms I3 zu Null
gewählt wurde, ist der komplexe Zeiger I3 = 4.0mA rein reell ohne Imaginärteil. Damit lassen
sich die komplexen Spannungen U 5 , U 6 und mit der Kirchhoffschen Maschenregel U 4
berechnen:
U 6 = I3 ⋅ R
U 5 = I 3 ⋅ jωL 2
= 4.0mA ⋅ 1.0kΩ
= 4. 0V
= 4.0mA ⋅ j0.75kΩ
= j3.0V
U 4 = U 6 + U 5 = 4.0V + j3.0V
Auch hier ergibt sich der Betrag U4 der Spannung an der Kapazität C mit Hilfe von Pythagoras:
U4 = U4
=
[Re(U 4 )]2
+
[Im(U 4 )]
=
4.0 2 + 4.0 2 V
=
5.0V
1.2.2 Zeigerdiagramm 2. Schritt:
Mit Hilfe der Spannung U 4 läßt
sich der Strom I 2 durch die Kapazität C ermitteln. Der Strom
durch eine Kapazität kommt ja um
eine Viertelperiode früher, als die
Spannung. Deswegen muß der
Stromzeiger I 2 senkrecht zu U 4
_I 2
nach oben zeigen. Die Länge des
Zeigers muß mit Hilfe des Betrags
U4 der Spannung U 4 an der
U
_4
U
_6
U
_5
_I 3
Kapazität berechnet werden.
Übungsblatt_B5_1z.doc
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
03.01.04 15:41 Uhr
Prof. Dr. Höcht
Grundlagen der Elektrotechnik
3
Übungsaufgaben zur Wechselstromtechnik mit Lösung
Berechnung mit Hilfe des Zeigerdiagramms
Die Länge I2 des Stromzeigers I 2 ergibt sich aus der Länge U4 des Spannungszeigers und des
Betrags des kapazitiven Widerstandes 1 ωC :
1
I 2 = I 2 = U 4 ⋅ ωC = 5.0V ⋅
= 4.05mA
1.236kΩ
Berechnung mit Hilfe der komplexen Darstellung:
Der Stromzeiger I 2 ergibt sich aus der Division des Spannungszeigers
U 4 = 4.0V + j ⋅ 3.0V und des kapazitiven Widerstandes von C2 mit
1
1
= ⋅1.236kΩ = − j ⋅1.236kΩ
j ⋅ ωC 2
j
I2 =
U4
1 j ⋅ ωC 2
=
4.0V + j ⋅ 3.0V
= − 2.43mA
− j ⋅1.236kΩ
+
j ⋅ 3.24mA
Dies ist die Koordinate der Spitze des I 2 -Zeigers im obigen Zeigerdiagramm. Die Länge des
Stromzeigers (= Betrag des Stroms I2) ergibt sich mit Pythagoras zu
I 2 = I 2 = 2.432 + 3.24 2 mA = 4.05mA
und liefert dasselbe Ergebnis, wie die Berechnung mit Hilfe der Zeigerdarstellung.
1.2.3 Zeigerdiagramm 3.
Schritt:
Aus den bekannten
Strömen I 2 und I3
_I 3
_I 2
_I 1
läßt sich mit der Kirchhoffschen Knotenpunktregel der Eingangsstrom I1 in die GesamtU
_4
schaltung ermitteln.
Dazu müssen lediglich
die beiden Zeiger addiert werden.
U
_6
U
_5
_I 3
Berechnung mit Hilfe des Zeigerdiagramms
Der resultierende Stromzeiger I1 kann zwar leicht gezeichnet werden. Da aber hier keine rechten
Winkel mehr auftauchen, ist die Berechnung des Betrags I1 unmittelbar nicht möglich. Bestenfalls
läßt sich die Länge direkt aus der Zeichnung ablesen. Hier ist daher für die weiteren Berechnungen der Weg über die komplexe Rechnung erforderlich.
Übungsblatt_B5_1z.doc
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
03.01.04 15:41 Uhr
Prof. Dr. Höcht
Grundlagen der Elektrotechnik
4
Übungsaufgaben zur Wechselstromtechnik mit Lösung
Berechnung mit Hilfe der komplexen Darstellung:
Die komplexe Darstellung der Ströme I1 und I 2 ist von oben her bekannt. Damit läßt sich die
Koordinate der Spitze des I1 -Zeigers berechnen:
I1 =
I 2 + I3
=
− 2.43mA + j ⋅ 3.24mA
+
4.0mA
= 1.57mA + j ⋅ 3.24mA I
Der Betrag I1 ergibt sich mit Pythagoras zu
I1 = I1
=
1.57 2 + 3.24 2 mA
=
3.60mA
Der Nullphasenwinkel ϕ I1 von I1 folgt aus Real- und Imaginärteil mit der Tangensfunktion:
Im I1
3.24
ϕ I1 = arctg
= arctg
= 64.15°
1.57
Re I1
{}
{}
1.2.4 Zeigerdiagramm 4. Schritt:
Nachdem nun der Eingangsstrom I1 nach Betrag und Phase bekannt
ist, lassen sich auch mit
Hilfe des Zeigerdiagramms die Spannungen
an der Induktivität L1 und
der Kapazität C1 ermitteln. Gegenüber dem eben
ermittelten Stromzeiger
I1 eilt die Spannung U 2
_I 3
_I 1
_I 2
U
_2
U
_4
U
_5
U
_6
an der Induktivität um 90°
_I 3
U
vor, die Spannung an der
_3
Kapazität um 90° nach.
Mit dem Ergebnis für
I1 = I1 = 3.60mA und den Widerstandswerten für L1 und C1 lassen sich auch die Längen der
beiden Spannungszeiger berechnen und in das Zeigerdiagramm eintragen.
Berechnung mit Hilfe des Zeigerdiagramms
Die Länge U2 des Spannungszeigers U 2 an der Induktivität L1 wird berechnet aus dem Betrag
des Eingangsstroms I1 und dem induktiven Widerstand ωL1 :
U 2 = U 2 = I1 ⋅ ωL 2 = 3.60mA ⋅ 2.0kΩ = 7.20V
Analog ergibt sich der Spannungsabfall U3 längs der Kapazität C1:
I1
U 3 = U3 =
= 3.60mA ⋅1.0kΩ = 3.60V
ωC1
Übungsblatt_B5_1z.doc
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
03.01.04 15:41 Uhr
Prof. Dr. Höcht
Grundlagen der Elektrotechnik
5
Übungsaufgaben zur Wechselstromtechnik mit Lösung
Berechnung mit Hilfe der komplexen Darstellung:
Die Koordinaten der Zeigerspitzen von U 2 und U 3 ergeben sich aus der Multiplikation des
komplexen Eingangsstroms I1 mit den Blindwiderständen j ⋅ ωL1 und 1 j ⋅ ωC1 :
U 2 = I1 ⋅ j ⋅ ωL1 = (1.57 mA + j ⋅ 3.24mA ) ⋅ j ⋅ 2.0kΩ
U 3 = I1 ⋅
=
1
1
= (1.57mA + j ⋅ 3.24mA ) ⋅ 1.0kΩ
j
j ⋅ ωC1
=
− 6.48V + j ⋅ 3.14V
+ 3.24V − j ⋅1.57V
1.2.5 Zeigerdiagramm 5. Schritt:
Die Eingangsspannung U1 folgt aus der Kirchhoffschen Maschengleichung
U1 = U 2 + U 3 + U 4
_I 3
_I 2
_I 1
U
_3
U
_4
U
_1
U
_4
U
_2
U
_5
U
_6
_I 3
U
_3
Berechnung mit Hilfe des Zeigerdiagramms:
Die Eingangsspannung U1 läßt sich nur im Rahmen der Zeichengenauigkeit graphisch ermitteln.
Dazu werden die Zeiger U 2 , U 3 und U 4 aneinandergehängt. Die Länge des Zeigers muß gemessen und mit dem Zeichnungsmaßstab in den Betrag U1 der Eingangsspannung
U1 umgerechnet
werden. Ebenso kann die Phasenlage ϕ U1 der Eingangsspannung als Winkel zwischen dem Zeiger U1 und der Abszisse (= reelle Achse) ermittelt werden. Genauer und einfacher ist hier aber
die Berechnung mit Hilfe der obigen Ergebnisse.
Berechnung mit Hilfe der komplexen Darstellung:
U1 = U 2
− 6.48V + j ⋅ 3.14V
+ U3
+ 3.24V − j ⋅ 1.57V
+ U4 =
+ 4.0V +
j ⋅ 3. 0 V
=
0.76V + j ⋅ 4.57V
Übungsblatt_B5_1z.doc
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
03.01.04 15:41 Uhr
Prof. Dr. Höcht
Grundlagen der Elektrotechnik
6
Übungsaufgaben zur Wechselstromtechnik mit Lösung
Für den mit dem Voltmeter meßbaren Betrag der Eingangsspannung U1 gilt:
U 1 = U1 = 4.63V
Der Nullphasenwinkel ϕ u der Spannung beträgt
Im U1
4.57
ϕ u = arctg
= arctg
= 80.56°
0.76
Re U1
{ }
{ }
Mit dem Nullphasenwinkel ϕI1 des Stroms I1 aus 1.2.3 folgt für die Phasenverschiebung ϕ
zwischen Eingangsspanung U1 und Eingangsstrom I1 :
ϕ = ϕ U1 − ϕI1
1.2
= 80.56° − 64.15° = 16.41°
Gesamtimpedanz der Schaltung
Lösung mit Hilfe des Zeigerdiagramms
Aus dem Zeigerdiagramm sind die Spannung U1 = U1 , der Strom I1 = I1 und die Phasenverschiebung ϕ bekannt. Damit ergibt sich die Impedanz Z =
stand Z =
U1
und der komplexe WiderI1
U1 j16.41°
U
⋅e
= 1 (cos16.41° + j ⋅ sin 16.41°)
I1
I1
Lösung mit Hilfe der komplexen Rechnung:
Hier ist es zunächst zweckmäßiger, den komplexen Widerstand Z =
U1
I1
zu berechnen. Der
Im{Z}
Re{Z}
des komplexen Widerstandes liefert die Phasenverschiebung zwischen Spannung und Strom.
Betrag des komplexen Widerstandes Z ergibt dann die Impedanz, der Winkel ϕ = arctg
Berechnung mit Hilfe des Zeigerdiagramms
Z =
U1
4.63V
=
= 1.286kΩ
I1
3.60mA
Z = 1.268 ⋅ e j16.41° kΩ = 1.286kΩ ⋅ (0.959 + j ⋅ 0.283) = 1.23kΩ + j ⋅ 0.36kΩ
Berechnung mit Hilfe der komplexen Rechnung
Z =
0.76V + j ⋅ 4.57V
(0.76 + j ⋅ 4.57 )⋅ (1.57 − j ⋅ 3.24)
=
1.57 mA + j ⋅ 3.24mA
(1.57 + j ⋅ 3.24 )⋅ (1.57 − j ⋅ 3.24)
= (1.23 + j ⋅ 0.36 )kΩ = 1.282kΩ ⋅ e j⋅16.3°
Die geringfügigen Unterschiede beim der Impedanz und der Phasenverschiebung ergeben sich aus
den Rundungsfehlern
Übungsblatt_B5_1z.doc
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
03.01.04 15:41 Uhr
Prof. Dr. Höcht
Grundlagen der Elektrotechnik
7
Übungsaufgaben zur Wechselstromtechnik mit Lösung
Aufgabe 2
Eine Leuchtstoffröhre mit Vorschaltdrossel (Induktivität u.a. zur Strombegrenzung) wird dargestellt als Serienschaltung eines ohmschen Widerstandes
R und einer idealen Spule (Induktivität L) ohne Verluste. Der ohmsche Widerstand nimmt eine Wirkleistung P = 40W auf. Durch die Leuchtstoffröhre
fließe ein Strom I eff = 0.40A . Die Gesamtschaltung liegt am Wechselstromnetz ( f = 50Hz ) mit U eff = 230V .
2.1
2.2
2.3
I
L
U
R
Scheinleistung S
S = U eff ⋅ I eff = 230V ⋅ 0.40A = 92VA
Leistungsdreieck
Komplexe Leistung aus der Wirkleistung P des ohmschen Verbrauchers und
der Blindleistung QL der Induktivität: S = P + jQ L
P
40 W
S = S = P 2 + Q L2 ,
cos ϕ =
=
= 0.43
S
92VA
S
Q
L
P
Größe des ohmschen Widerstands R und des Blindwiderstands ωL
Lösungsweg:
R:
Strom I und Wirkleistung sind bekannt. Daraus ergibt sich R
Die Blindleistung ergibt sich aus dem Leistungsdreieck. Mit dem Strom I ergibt sich
ωL :
daraus der Blindwiderstand ωL .
Berechnung:
R:
P = I2 ⋅ R
→
R =
P
I
2
=
40W
0.40 2 ⋅ A 2
= 250Ω
QL
ωL : Q L = I 2 ⋅ ω ⋅ L → ωL =
I2
QL =
2.3
S2 − P 2
=
92 2 − 40 2 var
ωL =
= 82.8 var
Kompensation der induktiven Blindleistung
Lösungsweg:
Zur Kompensation der induktiven Blindleistung gibt es folgende 2 Möglichkeiten:
- Serienschaltung einer Kapazität C
- Parallelstellung einer Kapazität C
0.40 2 ⋅ A 2
= 518 Ω
C
I
L
U
Bei der Serienschaltung einer Kapazität ändert sich der Strom
durch die Leuchtstoffröhre. Daher ist diese Möglichkeit der
Kompensation nicht möglich, da sich dann die Leistung der
Leuchtstoffröhre ändern würde. Somit bleibt die übliche Art
U
der Kompensation parallel zum Verbraucher, bei der die Kapazität zur Kompensation an derselben Spannung liegt, wie der
Verbraucher.
Zur Kompensation muß die induktive Blindleistung des Verbrauchers QL gleich der kapazitiven Blindleistung QC sein.
Übungsblatt_B5_1z.doc
83.8 ⋅ V ⋅ A
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
R
I
L
C
R
03.01.04 15:41 Uhr
Prof. Dr. Höcht
Grundlagen der Elektrotechnik
8
Übungsaufgaben zur Wechselstromtechnik mit Lösung
Berechnung Variante 1
An der Kapazität C liegt die Netzspannung U = 230V. Die kapazitive Blindleistung muß
Q L = 82.8 var sein.
QC =
U eff 2
1
ω⋅ C
=
U eff 2 ⋅ ω ⋅ C
1
ω⋅ C
→
=
U eff 2
230 2 ⋅ V 2
=
QL
82.8 ⋅ V ⋅ A
= 639Ω
Achtung! Der kapazitive Widerstand 1 ωC ist nicht gleich dem
induktiven Widerstand ωL , obwohl die Blindleistungen beider
Schaltelemente gleich groß sind! Ursache hierfür ist, daß an C die
volle Netzspannung liegt, während an L nur ein Teil davon abfällt. Diese
Zusammenhänge werden in der zweiten, etwas komplizierteren
Berechnungsart deutlich.
1
= 638.9Ω
→
ω⋅ C
1
A⋅s
C =
= 4.98 ⋅ 10 − 6
= 4.98µF
1
V
V
2 ⋅ π ⋅ 50 ⋅ ⋅ 638.9
s
A
Q
L
= 0 S
P
Q
Berechnung Variante 2
Die Serienschaltung der Leuchtstoffröhre mit Widerstand R und der
Drossel mit der Induktivität L wird im folgenden dargestellt als komplexer Widerstand Z und als Leitwert Y = 1 Z
C
Z = R + j ⋅ ωL = 250Ω + j ⋅ 518Ω
Y =
1
Z
=
=
(0.756
=
1
RP
1⋅ A
(250 + j ⋅ 518) ⋅ V
−
+
j ⋅ 1.566) ⋅ 10−3
=
(250
A
V
=
1
j ⋅ ωL p
=
Die Serienschaltung aus Leuchtstoffröhre und Drossel läßt sich also völlig
äquivalent darstellen als Parallelschaltung eines anderen ohmschen
U
Widerstandes R P = 1.323kΩ und
einer anderen Induktivität mit dem
Blindwiderstand ωL = 639Ω .
+
(250 − j ⋅ 518) ⋅ A
j ⋅ 518) ⋅ (250 − j ⋅ 518) ⋅ V
1
1.323kΩ
+
1
j ⋅ 639Ω
I
I
L
U
Lp
Rp
R
Der Zahlenwert des induktiven Parallelwiderstandes ωL p ist gleich dem oben berechneten Wert
Übungsblatt_B5_1z.doc
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
03.01.04 15:41 Uhr
Prof. Dr. Höcht
Grundlagen der Elektrotechnik
9
Übungsaufgaben zur Wechselstromtechnik mit Lösung
des kapazitiven Kompensationswiderstandes
1
. Daraus folgt, daß die Parallelschaltung
ωC
der Kapazität zur Induktivität LP und zum
ohmschen Widerstand RP auf einen rein ohmschen Gesamtleitwert Y = Y = Y und
damit natürlich auch ohmschen Gesamtwiderstand R p = 1.323kΩ führt, der an 230 V die
1/R p
1
j TL p
Y
Y
1/R p
1
j T Lp
j TC
gleiche Wirkleistung aufnimmt, wie die Leuchtstoffröhre mit R = 250Ω an der niedrigeren
Spannung 0.4A ⋅ 250Ω = 100V .
Die nebenstehenden Zeigerdiagramme zeigen
die Leitwerte vor- und nach der Kompensation. Vor der Kompensation
Übungsblatt_B5_1z.doc
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
Nach der Kompensation
03.01.04 15:41 Uhr
Prof. Dr. Höcht
Grundlagen der Elektrotechnik
10
Übungsaufgaben zur Wechselstromtechnik mit Lösung
Übungsblatt_B5_1z.doc
Fachhochschule München
Fachbereich Maschinenbau - Fahrzeug-/Flugzeugtechnik
03.01.04 15:41 Uhr
Prof. Dr. Höcht