2. Tag 550844 Lösung 6 Punkte Teil a) Wie in de

55. Mathematik-Olympiade
4. Stufe (Bundesrunde)
Olympiadeklasse 8
Lösungen – 2. Tag
c 2016 Aufgabenausschuss des Mathematik-Olympiaden e.V.
www.mathematik-olympiaden.de. Alle Rechte vorbehalten.
550844 Lösung
6 Punkte
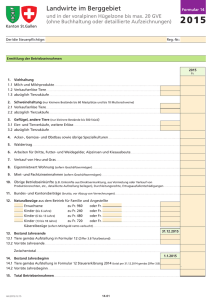
Teil a) Wie in der Abbildung L 550844 a angegeben, bezeichnen wir mit A, B, . . . , M einige
der Eckpunkte der Puzzleteile und mit α, β, γ, δ und ε die Größen der Innenwinkel der
Puzzleteile.
K
ε
L
J
δ δ
γ
E
M
γ
δ
I
H
Dε
C
Z
ε
β
F
α
G
Yε
X
α
A
B
L 550844 a
Wegen der Kongruenz der Puzzleteile wird der Vollwinkel um den Punkt A in sechs gleich
große Teile zerlegt, weswegen 6 · α = 360◦ und daher
(1)
α = 60◦
folgt. Durch Zerlegung des Achtzehnecks in 18 Dreiecke, bei denen der Punkt A ein Eckpunkt
ist und eine Seite des Achtzehnecks eine Seite des Dreiecks ist, erhält man 18 · 180◦ als Summe
der Größen der Innenwinkel aller 18 Dreiecke. Daher ist (18·180◦ −360◦ = ) 16·180◦ die Summe
der Größen der Innenwinkel des Achtzehnecks. Da die Innenwinkel des Achtzehnecks alle gleich
groß sind, ist (16 · 180◦ : 18 = ) 160◦ die Größe jedes der Innenwinkel des Achtzehnecks. Hieraus
folgt
(2)
ε = 160◦ .
Für den Vollwinkel um den Punkt Y gilt α + β + ε = 360◦. Wegen (1) und (2) folgt daher
(3)
β = 140◦ .
Für den Innenwinkel des Achtzehnecks beim Eckpunkt J gilt 2 · δ = ε. Wegen (2) folgt daher
(4)
δ = 80◦ .
1
Für den Vollwinkel um den Punkt D gilt 2 · γ + ε = 360◦. Wegen (2) folgt daher
(5)
γ = 100◦ .
Mit (1) bis (5) sind die gesuchten Größen der Innenwinkel eines solchen Puzzleteils bestimmt:
Es gelten α = 60◦, β = 140◦, γ = 100◦, δ = 80◦ und ε = 160◦.
K
J
L
I
E
M
H
D
C
Z
δ
α
ε
β
F
α
G
Y
X
α
A
B
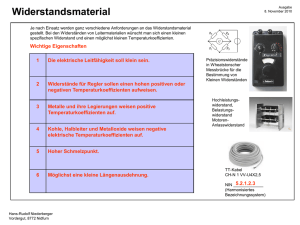
L 550844 b
Teil b) Zum Beweis der Behauptung zeigen wir, dass |XY Z| = 180◦ gilt.
Nach Teil a) gelten
|Y CX| = δ = 80◦
(6)
|Y AF | = |CY D| = |EF Z| = α = 60◦ ,
(7)
und
siehe Abbildung L 550844 b. Die Seiten AY , AF und F Z sind einander entsprechende Seiten
in den zueinander kongruenten Fünfecken ABXCY , AY DEF und F ELM Z. Daher gilt
(8)
|AY | = |AF | = |F Z| .
Wegen (8) ist das Dreieck AY F gleichschenklig und wegen (7) nach Basis- und Innenwinkelsatz
sogar gleichseitig. Daher gelten
(9)
|F Y A| = |AF Y | = 60◦
und
(10)
|F Y | = |AY | .
Aus (3) und (9) folgt
|DY F | = |DY A| − |F Y A| = 140◦ − 60◦ = 80◦ .
(11)
Aus (2), (7) und (9) folgt
|Y F Z| = |Y F E| + |EF Z| = (|AF E| − |AF Y |) + |EF Z|
= 160◦ − 60◦ + 60◦ = 160◦ .
2
(12)
Wegen (8) und (10) ist das Dreieck F Y Z gleichschenklig. Aus (12) sowie nach Basis- und
Innenwinkelsatz folgt daher
1
1
|ZY F | = · (180◦ − |Y F Z|) = · (180◦ − 160◦) = 10◦ .
(13)
2
2
Die Seiten AY und CY sowie AF und DY sind einander entsprechende Seiten in den zueinander kongruenten Fünfecken AY DEF und Y CIJD. Wegen (8) gilt daher
(14)
|AY | = |CY | = |DY | .
Die Seiten DY und CX sind einander entsprechende Seiten in den zueinander kongruenten
Fünfecken AY DEF und ICXGH. Daher gilt
(15)
|CX| = |DY | .
Wegen (14) und (15) ist das Dreieck CY X gleichschenklig. Aus (6) und nach Basis- und
Innenwinkelsatz folgt daher
1
1
|XY C| = · (180◦ − |Y CX|) = · (180◦ − 80◦) = 50◦ .
(16)
2
2
Aus (7), (11), (13) und (16) folgt schließlich
|XY Z| = |XY C| + |CY D| + |DY F | − |ZY F | = 50◦ + 60◦ + 80◦ − 10◦
= 180◦ .
Folglich liegen die Punkte X, Y und Z auf einer gemeinsamen Geraden.
550845 Lösung
7 Punkte
Wir beachten, dass eine natürliche Zahl genau dann durch 4 teilbar ist, wenn die aus ihren
letzten beiden Ziffern gebildete Zahl durch 4 teilbar ist. Sie ist genau dann durch 9 teilbar,
wenn ihre Quersumme durch 9 teilbar ist.
Teil a) Unabhängig davon, wie Anke spielt, kann Gert in diesem Fall gewinnen, wenn er
intelligent spielt. Wir geben eine Möglichkeit an, wie Gert auf Ankes Züge reagieren kann, um
den Sieg zu erzwingen:
Anke hat an die erste Stelle die 9 gelegt. Gert legt an die zweite Stelle die 7. Wir machen nun
eine Fallunterscheidung danach, ob und wann Anke die Ziffer 4 oder die Ziffer 8 legt.
Fall 1: Anke legt an die dritte Stelle die Ziffer 4 oder die Ziffer 8. Dann legt Gert an die vierte
Stelle entsprechend die Ziffer 8 oder die Ziffer 4.
Wenn Anke an die fünfte Stelle eine ungerade Ziffer legt, dann kann Gert die Ziffer 2
legen. Gert hat gewonnen, weil die gelegte Zahl auf 12, 32 oder 52 endet und daher
durch 4 teilbar ist. Wenn Anke an die fünfte Stelle eine gerade Ziffer legt, dann kann
diese Ziffer nur 2 oder 6 sein. Gert legt entsprechend die Ziffer 6 oder die Ziffer 2. Gert
hat gewonnen, weil die gelegte Zahl 974 826, 974 862, 978 426 oder 978 462 ist und diese
vier Zahlen durch 9 teilbar sind.
Fall 2: Anke legt an die dritte Stelle eine von 4 und 8 verschiedene Ziffer. Dann legt Gert eine
ungerade Ziffer. Die Ziffern 4 und 8 sind noch verfügbar.
Wenn Anke an die fünfte Stelle eine gerade Ziffer legt, kann Gert die Ziffer 4 oder die
Ziffer 8 legen und gewinnt, da die gelegte Zahl auf 24, 28, 48, 64, 68 oder 84 endet und
daher durch 4 teilbar ist. Wenn Anke an die fünfte Stelle eine ungerade Ziffer legt, dann
kann Gert die Ziffer 2 oder die Ziffer 6 legen. Gert hat gewonnen, weil die gelegte Zahl
auf 12, 16, 32, 36, 52 oder 56 endet und daher durch 4 teilbar ist.
3
Da die Fallunterscheidung vollständig ist, ist hiermit gezeigt, dass Gert stets gewinnen kann,
wenn er intelligent spielt.
Teil b) Unabhängig davon, wie Anke spielt, kann Gert auch in diesem Fall gewinnen, wenn
er intelligent spielt. Wir geben eine Möglichkeit an, wie Gert auf Ankes Züge reagieren kann,
um den Sieg zu erzwingen:
Anke hat an die erste Stelle die 4 gelegt. Gert legt an die zweite Stelle die 5. Wir machen nun
eine Fallunterscheidung danach, ob und wann Anke die Ziffer 9 legt.
Fall 1: Anke legt an die dritte Stelle eine von 9 verschiedene Ziffer z3 . Dann legt Gert an die
vierte Stelle die Ziffer z4 mit z4 = 9 − z3 . Dies ist möglich, da bisher 4, 5 und die von
beiden verschiedene Ziffer z3 gelegt wurden, weswegen z4 von 4, 5 und z3 verschieden ist.
Fall 1.1: Anke legt an die fünfte Stelle eine von 9 verschiedene Ziffer z5 . Dann legt Gert
an die sechste Stelle die Ziffer z6 mit z6 = 9 − z5 . Dies ist möglich, da bisher 4, 5,
z3 und z4 mit z3 + z4 = 9 und die von diesen verschiedene Ziffer z5 gelegt wurden,
weswegen z6 von 4, 5, z3 , z4 und z5 verschieden ist. Gert hat gewonnen, weil die
gelegte Zahl die Quersumme (4 + 5 + z3 + z4 + z5 + z6 = 9 + 9 + 9 = ) 27 hat und
daher durch 9 teilbar ist.
Fall 1.2: Anke legt an die fünfte Stelle die 9. Die Ziffern z3 und z4 können nicht 2 und
6 oder umgekehrt sein, da 2 + 6 6= 9 gilt. Folglich kann Gert die 2 oder die 6 legen.
Gert hat gewonnen, weil die gelegte Zahl auf 92 oder 96 endet und daher durch 4
teilbar ist.
Fall 2: Anke legt an die dritte Stelle die 9. Dann kann Gert an die vierte Stelle die 3 legen.
Wenn Anke an die fünfte Stelle die Ziffer 1 oder die Ziffer 7 legt, dann kann Gert an die
sechste Stelle die 2 legen und gewinnt, da 459 312 oder 459 372 gelegt wurde und beide
Zahlen durch 4 teilbar sind. Wenn Anke an die fünfte Stelle die Ziffer 2 oder die Ziffer
6 legt, dann kann Gert an die sechste Stelle die 8 legen und gewinnt, da 459 328 oder
459 368 gelegt wurde und beide Zahlen durch 4 teilbar sind. Wenn Anke an die fünfte
Stelle die Ziffer 8 legt, dann kann Gert an die sechste Stelle die 7 legen und gewinnt, da
die gelegte Zahl 459 387 durch 9 teilbar ist
Da die Fallunterscheidung vollständig ist, ist hiermit gezeigt, dass Gert stets gewinnen kann,
wenn er intelligent spielt.
550846 Lösung
7 Punkte
I. Es sei z eine vierstellige Zahl, die ein Vielfaches des Produktes der beiden zweistelligen
Zahlen ist, die unter Beibehaltung der Reihenfolge der Ziffern aus den ersten beiden Ziffern
und den letzten beiden Ziffern der vierstelligen Zahl gebildet werden. Dann gelten
z = 100 · x + y
(1)
z =n·x·y
(2)
und
mit zweistelligen, positiven Zahlen x und y und einer positiven ganzen Zahl n.
Wegen Gleichung (2) ist z durch x und y teilbar. Da z durch x teilbar ist, ist auch y wegen
Gleichung (1) durch x teilbar.
Folglich existiert eine positive ganze Zahl k mit
(3)
y = k · x.
4
Aus den Gleichungen (1), (2) und (3) folgt 100 · x + k · x = n · x · k · x und wegen x 6= 0
schließlich
(4)
100 + k = k · n · x .
Wegen der Gleichungen (3) und (4) sowie der Zweistelligkeit von y gilt n > 1. Wegen x ≥ 10,
y ≤ 99 und (3) folgt 1 ≤ k ≤ 9. Da k und k · n · x durch k teilbar sind, ist k wegen Gleichung
(4) auch ein Teiler von 100. Es kann folglich nur k ∈ {1, 2, 4, 5} gelten. Wir können daher
folgende Fallunterscheidung durchführen:
Fall 1: Es gelte k = 1. Aus Gleichung (4) folgt 101 = n · x. Da 101 eine Primzahl ist und
n > 1 gilt, folgt n = 101 und x = 1 im Widerspruch zur Zweistelligkeit von x.
Fall 2: Es gelte k = 2. Aus Gleichung (4) folgt 51 = n · x. Wegen der Primfaktorenzerlegung
51 = 3 · 17, der Zweistelligkeit von x und n > 1 kann nur n = 3 und x = 17 gelten.
Wegen Gleichung (3) folgt y = 34 und aus Gleichung (1) daher z = 1734.
Fall 3: Es gelte k = 4. Aus Gleichung (4) folgt 26 = n · x. Wegen der Primfaktorenzerlegung
26 = 2 · 13, der Zweistelligkeit von x und n > 1 kann nur n = 2 und x = 13 gelten.
Wegen Gleichung (3) folgt y = 52 und aus Gleichung (1) daher z = 1352.
Fall 4: Es gelte k = 5. Aus Gleichung (4) folgt 21 = n · x. Wegen der Primfaktorenzerlegung
21 = 3 · 7, der Zweistelligkeit von x und n > 1 erhalten wir keinen Lösungskandidaten
für diesen Fall.
Es kann daher nur z ∈ {1352, 1734} gelten.
II. Es gelten tatsächlich 1352 = 2 · 13 · 52 und 1734 = 3 · 17 · 34 mit den zweistelligen Zahlen
13 und 52 bzw. 17 und 34.
Aus I. und II. folgt, dass 1352 und 1734 alle gesuchten Zahlen sind.
5