Columna Vertebralis_Aufsatz - Columna Vertebralis

Columna Vertebralis Bezüge zwischen Anatomie, Musiktheorie und klassischer Geometrie Ulrich Michael Kraus München-Schwabing und Schwabmünchen, 24. Juni 2016
Denn wo das Strenge mit dem Zarten,
wo Starkes sich und Mildes paarten,
da gibt es einen guten Klang.
*
aus Friedrich Schiller:
‚Das Lied von der Glocke’
II
Inhalt:
A. Einleitung
B. Hauptteil
1. Menschliche Wirbelsäule und Brustkorb
Wirbel und Bandscheiben – Hals-, Brust- und Lendenwirbel – berippte und unberippte Wirbel – echte
und unechte Rippen – 7 obere und 5 untere - Zusammenfassung
2. Das Allgemeine in der Musik
Geräusche – Schall – Frequenz – Töne – Harmonie – Melodie – Klänge – Intervalle – Prim und Oktave
– Quarte und Quinte – perfekte Konsonanz – Umkehrintervalle/Komplementärintervalle – imperfekte
Konsonanz – Dissonanz – Zusammenfassung
3. Der Weg der westlichen Musik
Pentatonik – Heptatonik – Pythagoras – Monochord – Doppeloktave – Ganztöne – Tetraktys – Längenund Frequenzverhältnisse – Duodezime – Halbtöne – Limma – Zusammenfassung - Hexatonik –
Tritonus – Pythagoräisches Komma – Temperatur – chromatische Leitern – Quintenzirkel –
Tetrachorde – Modi – Dur- und Molltonleitern – Zusammenfassung – Pythagoräische Terz – Didymos
von Samos – Reine Stimmung – Großer und kleiner Ganzton – diatonische Leiter
4. Die Schemen von Wirbelsäule und Musik im Vergleich
Chromatische Töne und Rippenpaare – Wirbelzahl und Tonarten – Quinte und Quarte im Brustkorb
5. Zwischenbetrachtung: Der Weg der Altchinesischen Musik
12 Lü – pentatonische Leitern – heptatonische Leitern – Fazit
6. Geometrische Grundkörper und musikalische Verhältnisse
Das Grabmal des Archimedes – Kugel – Zylinder – Kegel – Pyramide – Dreieck – Parabelsegment
C. Schluss
Pythagoras und die Kugel – Sieben und Zwölf als rein mythische Zahl? – Unzenteilungen – Metrisches
System
D. Literaturverzeichnis
E. Anhang
III
A. Einleitung
Ziel dieser Arbeit ist es, Vergleiche zwischen menschlicher Anatomie, Musiktheorie und klassischer
Geometrie aufzuzeigen und zu belegen.
Wir werden zunächst die menschliche Wirbelsäule und den Brustkorb im Schema betrachten. Daneben
werden wir die Grundlagen der Musiktheorie darlegen. Wir wollen dabei allgemein vorgehen und die
mathematisch-physikalischen Voraussetzungen der Musik hervorheben. Nach den allgemeinen
Grundlagen soll die Entwicklung der westlichen Musik zusammengefasst werden. Der Bogen soll von
den ersten Saitenteilungen bis zu den diatonischen Tonleitern gespannt werden. Darauf wird ein erster
Vergleich folgen. In einer Zwischenbetrachtung soll ein Blick auf die Musiktheorie des alten Chinas
geworfen werden. Zuletzt werden wir ein Beispiel aus der klassischen Geometrie aufgreifen und
Parallelen zu den vorgelegten Wissensgebieten hervorheben. Im Anhang befinden sich Tafeln, die eine
abschließende Übersicht bieten.
-1-
B. Hauptteil
1. Menschliche Wirbelsäule und Brustkorb
Die menschliche Wirbelsäule besteht aus 24 Wirbeln. Sie beginnt oben am Schädel und folgt einer
Wellenbewegung nach unten. Dann geht sie in das Kreuzbein über und endet mit dem Steißbein. Auch
Kreuz- und Steißbein bestehen aus Wirbeln, nur sind deren Knochen fest miteinander verwachsen und
unbeweglich. Davon unterscheiden sich die oberen Wirbel, die durch Bandscheiben gelagert und somit
flexibel sind.
Von oben nach unten sortiert besteht die Wirbelsäule aus den folgenden Passagen:
1.
Sieben
(In
Halswirbel
der
Anatomie nummeriert als C1 bis C7).
2. Zwölf Brustwirbel (Th1 bis Th12).
3. Fünf Lendenwirbel (L1 bis L5).
4.
Kreuz-
und
Steißbein
(Sie
bestehen aus 5 bzw. 4 fusionierten
Wirbelknochen. Zählt man diese
neun ursprünglichen Wirbel hinzu,
ergibt sich eine Wirbelsumme von
33.)
Jede
dieser
vier
Passagen
gekennzeichnet
durch
ist
eine
Krümmung zur Bauch- bzw. zur
Rückenseite
hin:
Die
Halswirbel
wölben sich bauchseitig (ventral), die
Brustwirbel wölben sich rückseitig
(dorsal), die Lendenwirbel wölben
sich wieder bauchseitig, Kreuz- und
Steißbein
wölben
sich
wieder
rückseitig (vgl. Abb. 1). In der
Seitenansicht der Wirbelsäule ergibt
sich eine Wellenlinie.
Was
unterscheidet
nun
die
Abbildung 1 aus Frank H. Netter: Atlas der Anatomie des Menschen
genannten 24 Wirbel voneinander? (Stuttgart 1997).
Wer
allgemein
vorgeht,
kann
unterscheiden in Wirbel mit Rippen und Wirbel ohne Rippen:
12 Wirbel tragen eine Rippe – das sind die Brustwirbel.
12 Wirbel tragen keine Rippe – das sind die Halswirbel oder Lendenwirbel.
-2-
Oberhalb des Brustkorbs finden sich 7 rippenlose Wirbel, die Halswirbel - unterhalb des Brustkorbs
finden sind 5 rippenlose Wirbel, die Lendenwirbel. Sie sind nach dem Schema 7 obere und 5 untere
angeordnet. In Summe ergeben sie 12.
Was die 12 berippten Wirbel (Th 1-12) betrifft, so sind auch sie untereinander keineswegs gleich. Sie
alle tragen Rippen, doch sind diese in ihrem Bau unterschiedlich: In der Anatomie wird in echte und
unechte Rippen unterschieden (Costae verae und Costae spuriae). Die echten Rippen sind über
Rippenknorpel mit dem Brustbein (Sternum) verwachsen, die unechten Rippen stehen entweder frei in
den Brustkorb oder sind nur indirekt über Sehnen an das Brustbein angeschlossen. Die echten
Rippenpaare sind 7 an der Zahl, die unechten sind 5. Wie bei den rippenlosen Wirbeln zeigt sich das
Schema 7 obere und 5 untere.
12 = 7 obere + 5 untere
Abbildung 2: Knöcherner Teil der Rippen (aus Waschke/Böckers/Paulsen: Anatomie - Das Lehrbuch, S.136)
Da hier das "Schema" der menschlichen Wirbelsäule besprochen wird, wurde auch der anatomische
Normalfall beschrieben. Der Vollständigkeit halber soll noch erwähnt werden, dass die Natur – wie
eigentlich überall, auch hier Ausnahmen kennt: Etwa 5% der Menschheit leben mit einer variierten
Wirbelzahl – und nicht selten bleibt dies ein Leben lang unbemerkt. Tatsächlich sind Wirbelsäulen mit
23 bis 26 Wirbeln durchaus möglich – doch seien uns diese Varianten die berühmten Ausnahmen, die
die Regeln bestätigen.1 Und wie lauten diese Regeln? Wir fassen zusammen:
1
Moore, Persaud, Torchia: Embryologie, S.427
-3-
• Eine menschliche Wirbelsäule besteht aus 24 Wirbeln, die durch Bandscheiben gelagert
sind. Darunter befinden sich Kreuz- und Steißbein, die aus 9 weiteren Wirbeln
zusammengewachsen sind und ohne Bandscheiben auskommen. Sie sind darum keine
eigentlichen Wirbel.2
• 12 Wirbel sind rippenlos. Sie unterscheiden sich in 7 (obere) Halswirbel und fünf (untere)
Lendenwirbel. (Vertebrae cervicales und V. lumbales)
• 12 Wirbel sind berippt. Sie formen gemeinsam den Brustkorb, wobei die Rippen der oberen
7 Wirbel "echt" sind, während die unteren 5 "unecht" sind. Unecht heißen sie, da sie nicht
an das Brustbein (Sternum) angewachsen sind. Sie stehen frei in den Brustkorb, oder sind
durch Sehnen an die echten Rippen angeschlossen.
• Für berippte und unberippte Wirbel gilt das Schema: 12 = 7 obere + 5 untere.
• Der Brustkorb besteht aus 12 Rippenpaaren, also 24 Rippen - wobei auch hier gilt: 12 = 7
obere ("echte") + 5 untere ("unechte").
• Die 12 rippenlosen Wirbel neigen sich bauchseits (ventral) und stehen vor der Körperachse.
| Die 12 berippten Wirbel neigen sich rückseits (dorsal) und stehen hinter der Körperachse.
2
Zum Vergleich: Im Anhang befindet sich eine Tabelle mit den Wirbelzahlen diverser Nutztiere.
-4-
Abbildung 3: aus Frank H. Netter: Atlas der Anatomie des Menschen (Stuttgart 1997).
Nach dieser anatomischen Einteilung der menschlichen Wirbelsäule und des Brustkorbs, geht es im
nächsten Kapitel um die Grundlagen der Musiktheorie.
-5-
2. Das Allgemeine in der Musik
Wir erleben den Alltag als eine Ansammlung von Geräuschen. Unser Ohr nimmt beinahe ständig ein
Klappern, Brausen, Knallen oder Murmeln der Umgebung auf. Die Voraussetzung für das Geräusch ist
der Schall. Schall entsteht durch Druckschwankungen eines Trägermediums. Üblicherweise handelt es
sich hierbei um Luft, natürlich können aber auch Wasser oder feste Körper schallen. Untersucht man
Geräusche im Labor, zeigt sich, dass ihre Schallwellen unstetig ausfallen. Sie steigen stark an und fallen
schnell ab und meist sind sie eine Überlagerung diverser Wellen ohne Gemeinsamkeiten. Da unser Ohr
wenig oder kein Regelmaß heraushören kann, empfinden wir Geräusche als mehr oder weniger
strapazierend. Von Musik kann noch keine Rede sein.
Beginnt ein Gegenstand jedoch gleichmäßige Schallwellen auszusenden, erkennt unser Ohr eine
Frequenz dahinter. Frequenz drückt aus, mit wie vielen Anschlägen pro Zeiteinheit ein Ton übermittelt
wird. Die übliche Einheit "Hertz" bedeutet Anschläge pro Sekunde (Einheit: 1/s). Langsame Frequenzen
kann das Ohr noch als einzelne Anschläge wahrnehmen, steigt aber die Frequenz, so werden die
Anschläge zu einem Summen, dessen "Höhe" mit der Frequenz steigt. Das kann man beim Starten von
Motoren deutlich hören. Ähnlich wie im Kino, wo einzelne Dias zum Film beschleunigt werden,
verschmelzen in der Musik einzelne Schallanschläge zu Tönen. So verläuft der Weg vom Geräusch zum
Ton. Er zeichnet sich durch folgende Eigenschaften aus:
Einteilung nach E. SCHRÖDER:
"1. Seine Schwingungen sind regelmäßig.
2. Die Frequenz ist feststehend.
3. In seiner reinen Form ist er frei von Oberschwingungen.
4. Lautstärke und Schwingungsweite stehen in mathematischer Beziehung."3
Erklingt nun ein zweiter solcher Ton, kann unser Ohr (oder das Gehirn dahinter) beurteilen, ob die Töne
gleich waren oder verschieden. Waren die Töne verschieden, so gibt es zwei Möglichkeiten: Entweder
sie erklingen gemeinsam, dann wird daraus eine Harmonie, oder sie erklingen nacheinander, dann wird
daraus eine Melodie. In beiden Fällen aber vergleicht das Gehirn die Töne. Und so wie unser Auge bei
Interesse scharf stellt und hinsieht, so stellt auch unser Ohr "scharf" und lauscht auf. Dieses Aufhorchen
des Menschen ist eigentlich schon der Beginn der Musik. Ihn können wir bei festlichen Anlässen
nachvollziehen: Wird in einer Menschenrunde mit Krügen, Flaschen, Bierdosen oder Pappbechern
angestoßen, so ergeben sich dumpfe Geräusche, die wenig Aufmerksamkeit verdienen. Stoßen wir
allerdings mit schönen, gläsernen Kelchen an, so erklingt ein Ton. Unsere Ohren nehmen kein dumpfes
Geräusch wahr, sondern einen Klang, der unsere Aufmerksamkeit kurz fesselt und ein Gefühl der
Gemeinsamkeit hinterlässt. Alle lauschen einen Augenblick auf und sehen sich möglichst in die Augen.
Es treffen Töne aufeinander und überlagern sich, es entstehen Klänge.
Je nach Füllstand der Gläser, können die Töne die ihnen entweichen, verglichen werden. Sind die Gläser
gleich gefüllt und gleich beschaffen, so sind auch deren Töne die selben; sind sie hingegen
unterschiedlich gefüllt oder unterschiedlich beschaffen, so sind auch deren Töne unterschiedlich. Von
nun an spielen Intervalle eine Rolle. Sie drücken nämlich aus, wie weit produzierte Töne
3
Schröder: Mathematik im Reich der Töne, S.11
-6-
auseinanderliegen. Das neutrale Intervall ist die Prim. Sie beschreibt gleiche Töne und entspricht dem
neutralen Faktor 1. (Da Frequenzen multipliziert werden, ist die Eins das neutrale Element – nicht die
Null). Nach der Prim kommt die Oktave. Sie entspricht der 2, denn Oktave bedeutet, dass ein Ton die
doppelte Frequenz seines Vorgängers erreicht hat. (Zum Beispiel liegt die Oktave eines Tones mit 400
Hz bei 800 Hz.) Die Schallwellen dieser Töne überlagern sich denkbar gut und werden vom Ohr als
wohlklingend und ausgeglichen wahrgenommen. Wir empfinden Oktaven als gleiche Töne
unterschiedlicher Höhe.
Bis zu diesem Punkt ist Musik naturgegeben. Sie drückt sich rein mathematisch-physikalisch aus und
kulturelle Prägungen spielen noch keine Rolle. Diese beginnen erst, wenn Tonintervalle, die zwischen
der Oktave liegen, sortiert und zu Leitern zusammensetzt werden.
Wichtige Intervalle nach der Oktave sind Quinte und Quarte. Die Quinte liegt beim Frequenzverhältnis
3:2, die Quarte bei 4:3. Sie sind die Intervalle Nummer 3 und 4. Da auch ihre Verhältnisse noch
mathematisch einfach sind, nehmen wir sie als konsonant wahr. Ihre Schallwellen überlagern sich
ordentlich und ergeben viele gemeinsame Vielfache. Oktaven, Quarten und Quinten gelten gemeinhin
als angenehme Intervalle und werden eigentlich von allen Menschen als wohlklingend empfunden. Sie
heißen deshalb perfekte Konsonanzen. Außerdem sind Quarte und Quinte das Umkehrintervall des
anderen. Das bedeutet: eine Oktave kann durch eine Quarte und eine Quinte in Folge überwunden
werden.
(Quinte + Quarte = Oktave)
Rechnerisch drückt sich das so aus:
3 4 2
× = 2 3 1
Beispielsweise ist es vom c1 zum g1 eine Quinte und vom g1 zum c2 eine Quarte. Zusammen ergibt dies
eine Oktave (c1 → c2). Zudem bringt eine fallende Quinte (c2 → f1) den gleichen Ton wie eine steigende
Quarte (c2 → f2). Da sie sich ergänzen, werden Umkehrintervalle auch Komplementärintervalle genannt.
So gesehen sind auch Prim und Oktave Komplementärintervalle, da sie sich zur Oktave ergänzen.
Auf die konsonanten Intervalle folgen solche, die wir als nicht als ausgesprochen wohlklingend, aber
auch nicht als dissonant wahrnehmen. Das sind die Terzen und ihre Umkehrintervalle die Sexten. Sie
heißen imperfekte Konsonanzen. Die Frequenzverhältnisse sind 5:4 für die große Terz und 6:5 für die
kleine Terz. Verrechnet mit der Oktave 2:1 ergeben sich analog folgende Umkehrintervalle: 8:5 und für
die kleine Sexte und 5:3 für die große Sexte.
Als unausgewogen werden Sekunden und Septimen wahrgenommen. Sie heißen Dissonanzen. Je
komplizierter das mathematische Verhältnis zweier Töne, desto dissonanter ihr gemeinsamer Klang. Die
große Sekunde liegt bei 9:8. Völlig dissonant ist zuletzt das Verhältnis eines Tonpaares, das drei
Ganztöne auseinanderliegt. Sein Verhältnis beträgt 32:45. Im Lexikon der Harmonielehre finden wir eine
Gegenüberstellung von Intervall und Proportion:
-7-
Intervall
Proportion
Oktav
1:2
Quint
2:3
Quart
3:4
Große Sext
3:5
Große Terz
4:5
Kleine Terz
5:6
Kleine Sext
5:8
Kleine Septim
5:9
Große Sekund
8:9
Große Septim
8:15
Kleine Sekund
15:16
Tritonus4
32:45
Tabelle 1 nach R.Amon, Lexikon d. Harmonielehre (S.124): Je einfacher die Proportion, desto konsonanter das Intervall.
Diese Intervalle lassen sich paarweise zu Komplementärintervallen zusammenfassen, da sie gemeinsam
jeweils eine Oktave ergeben. Es handelt sich um vier Paare:
Prim - Oktave | Quinte - Quarte | Terz - Sexte | Sekunde - Septime
Sie können an zwei Händen zum Studium veranschaulicht werden: Man trage die 8 Intervalle der Reihe
nach auf die 8 äußeren Finger auf.
Tritonus bedeutet ein Intervall von 3 Ganztönen (wörtl. „Tritonus“). Er findet sich auf dem Klavier z.B.
im Intervall C-FIS.
4
-8-
Abbildung 4: Komplementärintervalle auf den Händen – Gleiche Finger bedeuten Komplementärintervalle.
Aus diesen Intervallen können Tonleitern innerhalb der Oktave gebaut werden. Dabei gibt es große
kulturelle Unterschiede, Varianten und Empfindsamkeiten. Auch Zwischentöne (Blue Notes) sind
bekannt. Dennoch ist der Gebrauch von Tonleitern allgemein.
Zusammenfassend lässt sich sagen:
• Die Anfänge der Musik sind naturgegeben, da sie von Mathematik und Physik bestimmt
sind. Kulturgegebenheiten treten erst später hinzu.
• Geräusche zeichnen sich durch unstete Schallwellen – Töne durch periodische
Schwingungen aus.
• Wichtigstes Intervall nach der Prim ist die Oktave. Sie beschreibt einen Ton, der als der Prim
gleich empfunden wird (halbierte oder verdoppelte Frequenz).
• Quinten und Quarten werden durchaus als konsonant empfunden, da sich ihre Schallwellen
mathematisch einfach ausdrücken lassen 3:2 bzw. 4:3. Je komplizierter das mathematische
Verhältnis zweier Töne wird, desto dissonanter wird das Intervall empfunden.
-9-
3. Der Weg der westlichen Musik
Für einfache Melodien genügt es, fünf Töne innerhalb der Oktave zu wählen und zu nutzen. Tatsächlich
kommen zahlreiche Kinderlieder oder Werbemelodien mit nur fünf Tönen innerhalb der Oktave aus.
Man nennt diese Methode des Komponierens Pentatonik. Sie taucht in vielen Kulturkreisen und
Musiksystemen auf. Sie ist einfach aber wirkungsvoll. In der westlichen Musik wurde es allerdings bereits
in der Antike üblich, eine Tonleiter aus sieben Tönen zu bauen. Deshalb der Begriff Oktave, denn die
Oktave ist der achte Ton einer solchen Leiter. Er gleicht wieder dem ersten. Die Methode aus sieben
Tönen Leitern zu bauen nennt man Heptatonik. Sie kennt viele Möglichkeiten und Varianten.
Theoretisch gehen sie auf Pythagoras von Samos (ca. 570 – 510 v. Chr.) und seine Schüler zurück. Anhand
von unterteilten Saiten gelang es ihnen, Tonabstände in Verhältnissen, also rationalen Zahlen (Brüchen)
auszudrücken. Am Monochord – einem Instrument mit gespannter Saite auf einem Klangkörper, konnte
dies demonstriert werden: Die Halbierung der Saite bringt die Oktave (1:2). Eine weitere Halbierung
bringt die Doppeloktave (1 2 × 1 2 = 1 4). Diese Teilung zeigt sich bis heute an der Gitarre: Der
zwölfte Bund jeder Saite markiert die Oktave. Er liegt exakt bei der Saitenhälfte.5
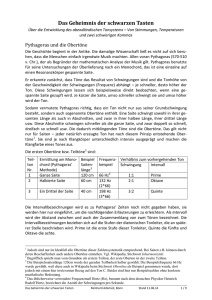
Des Weiteren fand Pythagoras bei 2/3 seiner Saite die Quinte, und bei 3/4 die Quarte. Der Sprung von
der Quarte zur Quinte galt ihm als Ganzton. Rechnerisch musste er sich so ausdrücken:
2 3 𝑎
= × 3 4 𝑏
(Quinte = Quarte + Ganzton)
Da die Lösung der Gleichung 𝑎 𝑏 = (8 9) beträgt, war hiermit der Ganzton definiert.
Da die vier Zahlen 1,2,3 und 4 genügten, die ersten Intervalle rational zu beschreiben, pries er diese als
heilige „Tetraktys“. Dabei handelt es sich nicht um Zahlenmystik, denn tatsächlich liefern bis heute nur
die Brüche der ersten vier Zahlen perfekte Konsonanzen (1:2, 1:3, 1:4, 2:3 und 3:4). Die höheren Zahlen
bieten nur noch imperfekte Konsonanzen (4:5, 5:6 etc.) oder Dissonanzen.
Wir haben anfangs die Frequenzverhältnisse von Schallwellen als Intervalle besprochen. Die Oktave
entspricht einer doppelten Wellenfrequenz, die Quinte einer eineinhalbfachen usw. Bei der
Saitenteilung zeigt sich, dass die Längenverhältnisse den Kehrbrüchen der Frequenzverhältnisse
entsprechen. Auch hier zeigen sich die Intervalle, allerdings im Kehrwert: 2:1 wird zu 1:2 und 3:2 wird zu
2:3. Dies zeigt sich deutlich am Monochord, auf dem Pythagoras 12 Bünde markierte:
Die Oktave lag bei 6/12 = 1/2.
Die Doppeloktave lag bei 3/12 = 1/4.
Die Quinte liegt bei 8/12 = 2/3.
Die Quarte liegt bei 9/12 = 3/4.
Es gibt auch E-Gitarren mit 24 Bünden. Hier kann man auch die Doppeloktave sehen: Sie teilt die
Saite so, dass genau 1 4 ihrer Länge schwingt.
5
- 10 -
Die Duodezime (die Quinte über der Oktave) liegt bei 1/3, denn 1 2 × 2 3 = 1 3.6
Abbildung 5: Durch die Zwölftelung einer Saite, können alle konsonanten Intervalle angeboten werden:
Oktave
1
𝟔
=
2 𝟏𝟐
Quinte
2
𝟖
=
3 𝟏𝟐
Quarte
Duodezime
1
𝟒
=
3 𝟏𝟐
3
𝟗
=
4 𝟏2
Doppeloktave
1
𝟑
=
4 𝟏𝟐
An diesem Teilungsschema hat sich bis heute nichts geändert. Es kann an jeder Gitarre studiert
werden:
6
W. Keil: Musikgeschichte im Überblick, S.30 ff.
- 11 -
Abbildung 6: Bis heute zeigen sich die pythagoräischen Verhältnisse auf der Gitarre. Den Sprung von der Quarte (5. Bund) zur
Quinte (7.Bund) definierte Pythagoras als Ganzton (GT).
- 12 -
Abbildung 7: Die konsonanten Intervalle auf der Gitarre. Sie finden sich durch Teilung der Saite in 12 gleiche Teile.
Soweit die Einteilung der grundlegenden Intervalle. Wie nun soll daraus eine Tonleiter werden? Die
Pythagoräer wählten die Quinte zur treibenden Kraft. Nach der Oktave sahen sie in ihr das reinste
Intervall. Von einem gewählten Ton stiegen sie drei Quinten nach oben und drei nach unten.
Angenommen dieser Ton sei das D, so vollzieht sich das wie folgt:
D
liefert in steigenden Quinten A-E-H, und in fallenden Quinten G-C-F. In Reihe lautet dies:
F-C-G-D-A-E-H
Nach aufsteigender Reihe sortiert, ergibt dies die Siebentonleiter: D - E - F - G - A - H - C
Darauf folgt wieder ein D als achter Ton, der dem ersten gleicht. Mit dem c vorangestellt entspricht eine
solche Leiter bereits unserer C-DUR-Skala. Sie besteht aus C - D - E - F - G - A - H – C. Das sind sieben Töne,
wobei der achte dem ersten gleicht.
Von da an wurde es kompliziert für Pythagoras und seine Nachfolger. Es wurde klar, dass zwischen dem
gefundenen E und dem F, weniger als ein Ganztonschritt liegt. Gleiches galt für den Abstand von H nach
- 13 -
C.
Es musste also einen Tonschritt geben, der kleiner sei als ein Ganzton: gewissermaßen ein Halbton.
Doch wie fand man ihn? Rechnerisch konnte der mathematisch exakte Halbton noch nicht gefunden
werden. Die Gleichung
8
𝑎
= ( )6 9
𝑏
(Ganzton = Halbton + Halbton)
ist nämlich mit keiner rationalen Zahl lösbar. Pythagoras – überzeugt "alles sei Harmonie und Zahl",
fand darauf keine Antwort. Der Überlieferung nach sollen Schüler, die diesen Mangel zur Sprache
brachten, verstoßen worden sein. Wir heute wissen, dass obige Gleichung nur mit der irrationalen Zahl
√2 lösbar ist:
8
2 2
=
9
3
6
Da irrationale Zahlen aber unerwünscht waren, behalf man sich mit dem Limma, einer rationalen Zahl,
die die Siebentonleiter rechnerisch ins Gleichgewicht brachte. Die Quarte setzt sich zusammen aus zwei
Ganztonschritten und einem Limma-Schritt.
(Quarte = Ganztonschritt + Ganztonschritt + Limma)
Rechnerisch bedeutet das:
8 8 243 15552 3
× ×
=
= 9 9 256 20736 4
Darauf folgte ein weiterer Ganztonschritt zur Quinte (Quinte = Quarte + Ganzton). Von dort war es
wieder eine Quarte zur vollendeten Oktave (Oktave = Quarte + Quinte). Mit dem Bruch 243/256 konnte
die Siebentonleiter in 5 Ganztonschritten und 2 Limma-Schritten ausbilanziert werden.
(Oktave = 5 Ganztonschritte + 2 Limma-Schritte)
8 8 8 8 8 243 243 1 934 917 632 1
× × × × ×
×
=
= 9 9 9 9 9 256 256 3 869 835 264 2
Mit dem Limma (griech. "Überbleibsel", "Reststück") konnte eine Tonleiter mit 5 Ganztonschritten und
2 Quasi-Halbtonschritten aufgestellt und arithmetisch rein formuliert werden.
Durch Pythagoras' Grundlagenarbeit war man sich im Alten Griechenland einig, dass eine Leiter in
sieben Stufen zu überwinden sei. Jede Tonleiter hatte darum Prim, Sekunde, Terz, Quarte, Quinte,
Sexte, Septime und Oktave. Darüber hinaus, war es aber diskutabel, wo Ganz- und Limmaschritten zu
setzen seien und bei welchem Ton man zu starten habe. Hier ergaben sich Varianten je nach Lage der
Limmaschritte und der Prim. Die Tonleitern, die daraus entstanden, wurden regional benannt und
hießen lydisch, ionisch, äolisch, phrygisch, dorisch etc.
- 14 -
Sie waren allesamt Siebentonleitern und wurden später im Mittelalter von der (jetzt) abendländischen
Musik fortgeführt.7
Wir fassen also zusammen:
• Die Grundlage unserer heutigen Tonleiteitern lieferten die Griechen, namentlich
Pythagoras, der an der Saite (dem Monochord) Teilungen vornahm und so Intervalle
markierte. Dies waren in erster Linie Oktave, Doppeloktave, Quinte, Quarte und
Duodezime. Da er dafür nur die ersten vier natürlichen Zahlen brauchte, galt ihm diese
"tetraktys" (Vierheit) als heilig.
• Den Raum zwischen Quarte und Quinte wies er dem Ganzton zu. Mit sechs dieser Ganztöne
kann eine Oktave grob überwunden werden, doch lässt sich dies arithmetisch nicht in Bilanz
bringen. Erst durch fünf Ganztonschritte und zwei Limma, den Vorgängern der
Halbtonschritte, lässt sich die Tonleiter sauber "rechnen". Somit stützt die Menge der
rationalen Zahlen (nämlich der Brüche), die Siebentonleitern. Diese werden auch als
diatonisch ("durch den Ton hindurch") bezeichnet.
• Die Frage, wo nun Ganztöne und Limma zu setzten seien und wo man eine Skala starte,
erklärt die zahlreichen Varianten griechischer Tonarten. Allgemein ist jedoch der Gebrauch
von sieben Tönen (Heptatonik).
Soviel zur Entstehung der Siebentonleitern. Aber warum gerade Siebentonleitern? Warum wird die
Oktave nicht mit 6 gleichen Ganztonschritten (also einer Hexatonik) überschritten? Rechnerisch
bedeutete dies, ein Verhältnis zu finden, dass in der Potenz 6 genau 1/2 ergibt.
(Ganzton + Ganzton + Ganzton + Ganzton + Ganzton + Ganzton = Oktave)
𝑎
𝑏
<
=
1
2
Die Lösung der Gleichung beträgt:
𝑎
=
𝑏
=
1
1
==
2
2
Dabei handelt es sich offenbar um keine rationale Zahl. Das bedeutet, es kann kein Bruch aus
natürlichen Zahlen gefunden werden, mit dem diese Tonleiter gerechnet werden kann. Gleiches zeigt
sich, wenn man das Verhältnis des gebräuchlichen Ganztones (8 9) mit sich selbst multipliziert:
8
9
<
= 0,493 …
Wir erreichten 1/2 nur gerundet. Eine Oktave mit sechs gleichen rationalen Verhältnissen zu überwinden
ist also nicht möglich. Würde man eine Oktave exakt sechsteln ergäbe sich eine irrationale Zahl.
Gleiches gilt auch, würde man die Oktave exakt siebteln (Ergebnis
@
1 2). Mit dem Rezept 5
Ganztonschritte + 2 Halbtonschritte kann jedoch eine rationale Lösung gefunden werden.
7
Da fast alle musiktheoretischen Quellen der Antike verschollen waren, konnte das Wissen der Griechen nur mit
Verwechslungen im Mittelalter reanimiert werden. Deshalb ist das griechische dorisch nicht dem mittelalterlichen dorisch
identisch.
- 15 -
Trotzdem kann auf einer heutigen Klaviatur die Oktave durch sechs Ganztonschritte überwunden
werden. Die Leiter C-D-E-FIS-GIS-AIS-C besteht nur aus Ganztonschritten. Wer diese allerdings auf dem
Klavier testet, wird sie als wenig anregend empfinden. Auch das hat Gründe: Die Leiter der sechs
Ganztöne führt über den Tritonus, der die Oktave exakt halbiert. Er liegt bei 3 Ganztönen – im obigen
Bespiel von C nach FIS. Sein Frequenzverhältnis ist äußerst dissonant. Wer mit hexatonischen Leitern
musizieren möchte, muss dieses Intervall in seine Musik aufnehmen. Durch pentatonsiche und
heptatonische Leitern wird der Tritonus umschifft – ein zweiter Grund warum sich diese durchgesetzt
haben.
Da nun die Pythagoräer durch ihre Siebentonleitern eine Seitenteilung entwickelt hatten, die ohne
Wurzelzahlen auskam, erschien ein neues Problem, das ihnen zu schaffen machte: Wenn Tonleitern
durch Schichtungen von Quinten gewonnen werden, dann müssten sich Oktav- und Quintsprünge
irgendwann wieder treffen. Von C ausgehend müsste man sowohl durch Quintenreihen wie durch
Oktavreihen wieder ein C erhalten. Die erste Quinte führt von C nach G, die zweite von G nach D, die
dritte von D nach A und so fort. Nach einigen Wiederholungen müsste die Quinte wieder auf ein C fallen,
welches dann mehrere Oktaven über dem ursprünglichen C liegt.
Gehen wir die Quintenreihe durch: C-G-D-A-E-H-FIS-CIS-GIS-DIS-AIS-EIS-HIS
Dies waren 12 Quintensprünge, die zu einem Ton "HIS" führen, der dem C fast gleich ist – aber eben
nur fast. Dieses "fast-c" liegt 7 Oktaven über unserem Ausgangs-C. Es ist dem C zum verwechseln
ähnlich, aber nicht gleich. Dieser Zirkel aus Quinten schließt sich nicht zum Ring, sondern läuft wie eine
Spirale weiter, wobei stets die Töne nach 12 Quinten, denen vor 7 Oktaven zum Verwechseln ähnlich
sind.
Dass sich Quinten und Oktaven nicht genau treffen können, zeigt sich daran, dass die Potenzen von 3 2
(=Quintsprung) und 2 1(=Oktavsprung) keine gemeinsamen Ergebnis haben: Zwölf Quinten das
A
6
6
B
bedeutet: ( )B6 ≈ 129,7. Sieben Oktaven das bedeutet: ( )D = 128
Diese Diskrepanz zwischen zwölf reinen Quinten und sieben reinen Oktaven heißt pythagoräisches
Komma. Für die Praxis bedeutet dies: Wenn ein Klavierstimmer von einem Grundton C in reinen Quinten
nach oben stimmt, bekommt er einen Ton HIS, der leicht anders klingt, als hätte er mit reinen Oktaven
nach oben gestimmt. Oder anders ausgedrückt: Er kann nicht makellose Oktaven und makellose
Quinten über die ganze Breite der Klaviatur anbieten. Eine Lösung kann darin bestehen, den
Unterschied des Kommas auf die Intervalle innerhalb der Oktave aufzuteilen. Der Fachbegriff hierfür
lautet „temperieren“ und das Ergebnis wird Temperatur genannt.8 Da der Musiker bei
Tasteninstrumenten keinen Einfluss auf die Abstimmung der Tonhöhen (Intonation) hat, müssen diese
immer minimal verstimmt sein. Der Tasten-Musiker bekommt ein vorgestimmtes Instrument und kann
durch sein Gehör nicht in die Intonation eingreifen. Streicher, Bläser und Sänger können dies zu jeder
Zeit – sie benötigen diese Maßnahmen also nicht.
Das pythagoräische Komma wurde vielfach als ein "Fehler der Natur" interpretiert. Fehlerhaft wäre die
Natur, wenn man erwartete, der Zirkel der Quinten müsse sich zu einem Ring schmieden lassen.
Johann Sebastian Bach verwendete die Temperaturen seines Zeitgenossen Andreas Werckmeister
(1645-1706). Sie begünstigten den Wechsel der Tonarten (Modulation). Bach schrieb in der Folge
einen Zyklus von Übungsstücken für Tasteninstrumente. Wegen der neuartigen Temperatur der
Instrumente gab er dem Übungsband den Titel: „Das Wohltemperierte Clavier“.
8
- 16 -
Vielmehr sieht die Natur eine Helix vor, in der wiederkehrende Töne wie Zwillinge verwechselbar, aber
nicht gesetzmäßig gleich sind. Im Lexikon der Harmonielehre von R. AMON lesen wir zu dem Thema:
"Die Aneinanderreihung von zwölf reinen Quinten ergibt keinen geschlossenen Kreis, sondern
eine Spirale. Die Oktav 1:2 wird durch die Primzahl 2, die Quint durch die Primzahl 3
repräsentiert." 9
Die dahinterliegende Ordnung – ob nun in Spiralform oder Ring lautet: 12 Quinten legen sich auf 7
Oktaven. Kehren wir noch einmal zu der Skala zurück, die Pythagoras durch Quintensprünge fand. Sie
lautete: D - E - F - G - A - H – C.
Beginnend mit C haben wir eine heutige C-Dur Tonleiter: C - D - E - F - G - A - H – C. Wollen wir nun aber
auf dem G eine Tonleiter bauen, die wiederum bis G läuft und gleiche Intervalle wie die C-Leiter hat, so
genügen diese angeführten Töne nicht. Es braucht einen weiteren Ton, der zwischen F und G liegt. Er
wurde FIS getauft. Wollen wir nun auf dem D eine dritte Tonleiter bauen, so genügt auch das FIS nicht
aus. Es braucht einen Ton der zwischen C und D liegt, sonst geht die Leiter nicht auf. Dieser Ton wurde
CIS getauft. Dieses
Spiel geht so lange bis fünf weitere dieser neuen Töne eingebaut sein werden. Nach
dem fünften Aushilfston kann das Spiel noch weiter getrieben werden, doch ergeben sich dann keine
neuen Hilfstöne mehr, sondern nur Töne, die schon bestanden. Diese Hilfstöne heißen CIS-DIS-FIS-GISAIS
oder DES-ES-GES-AS-B, je nachdem auf welchen Nachbarton sie sich beziehen. Dies bedeutet, dass
man unter Zuhilfenahme von 5 Zwischentönen (CIS-DIS-FIS-GIS-AIS) auf jedem einzelnen Ton der C-DurLeiter, wieder eine Leiter bauen kann.
Somit sind folgende Töne im Spiel: C-CIS-D-DIS-E-F-FIS-G-GIS-A-AIS-H. Das gibt zwölf Töne, die als
chromatisch bezeichnet werden. Wählt man sieben aus diesen zwölf Tönen für eine Tonleiter aus, so
kann mit Hilfe der fünf verbleibenden Töne auf jedem der sieben gewählten Töne eine neue Tonleiter
gebaut werden. Das Ordnungsschema hinter dieser Methode ist der Quintenzirkel. Er erlaubt dem
Tonsetzer seine Melodien systematisch auf eine Tonart seiner Wahl zu legen. Für die natürliche Tonleiter
C-D -E-F-G -A-H
bedeutet dies, dass auf jedem der Töne eine Leiter mit 5 Ganzton und 2 Halbtonschritten
errichtet werden kann. Wo nun diese Halbtonschritte zu liegen haben ist Geschmackssache, aber auch
hier bietet die Zwölftelung Vorteile:
Denken wir noch einmal an die Quarte. Sie ist nach Pythagoras einen Ganzton niedriger als die Quinte.
Demnach kann die Oktave als ein Paar von zwei Viertongespannen verstanden werden.
C-D-E-F | G -A-H-C
Diese Viertongespanne werden Tetrachorde genannt. Sie beschreiben eine Quarte von der Prim und
eine Quarte von der Quinte. Diese Quarten können unterschiedlich überwunden werden. Quarten
bestehen aus zwei Ganztönten und einem Limma (heute Halbton). Diese Schritte können auf drei
Weisen genommen werden:
Ganzton - Halbton - Ganzton
Halbton - Ganzton - Ganzton
9
Amon: Lexikon der Harmonielehre, Stichwort: Stimmungen - Mathematische Grundlagen, S.256
- 17 -
Ganzton - Ganzton - Halbton
Bei Zwölferteilung der Oktave können alle drei Varianten der Halbtonlage eingesetzt werden. Daraus
entstanden die "Modi" der Kirchentonarten, die sich je nach Lage der Halbtonschritte und des
Ausgangstones unterschieden. Nach dem Mittelalter setzten sich zwei Modi durch, die ionisch und
äolisch hießen. Ihre Tetrachorde hießen so:
1. Ganzton – Ganzton – Halbton | Ganzton – Ganzton – Halbton.
Schema (1-1-½-1-1-1-½) – das war ionisch und wurde zur Dur-Tonleiter
2. Ganzton – Halbton – Ganzton | Halbton – Ganzton – Ganzton
Schema (1-½-1-1-½-1-1) – das war äolisch und wurde die Moll-Tonleiter.
Wir fassen zusammen:
• In der westlichen Musik wird der Oktavraum in 12 gleiche Halbtöne gebrochen. Mit 12
dieser Intervalle wird eine Oktave überwunden.
• Aus diesen 12 Halbtönen (=Chromatik) wählt der Komponist 7 Töne für eine Tonleiter aus.
Aus C-CIS-D-DIS-E-F-FIS-G-GIS-A-AIS-H und C werden etwa D-E-FIS-G-A-H-CIS und D für D-Dur.
Durch die 12 chromatischen Töne können die Quarten der Tonleitern in drei
unterschiedlichen Dreischritten erreicht werden. Diese sind ganz-halb-ganz, halb-ganzganz und ganz-ganz-halb (vlg. C-D-DIS-F, C-CIS-DIS-F, C-D-E-F). Durch diese Varianz der
Dreischritte im "Tetrachord" der beiden Quarten, erklären sich die zahlreichen
Kirchentonarten, die von der Varianz Gebrauch machen.
• Auf dem Klavier kann leicht nachgezählt werden: Eine Quinte erreicht man durch sieben
Halbtonschritte (C nach G) eine Quarte durch deren fünf (C nach F). Gemeinsam ergeben
sich zwölf Halbtonschritte für die Oktave.
• Das Dur/Moll-System hält für jeden der 12 Töne im Oktavraum eine Tonleiter parat.
Zusammen ergibt dies 24 Tonleitern.
Nach Pythagoras wurden Verfeinerungen an diesem Teilungsschema vorgenommen, dennoch blieb es
im Wesentlichen bestehen. Wie oben beschrieben, lag das damalige Augenmerk auf den konsonanten
Intervallen, die durch Verhältnisse der Zahlen 1,2,3 und 4 darstellbar waren und bis heute sind.
Proportionen, die darüber hinaus gingen (Terzen oder Sexten), wurden vernachlässigt. Das sieht man
an der sog. pythagoräischen Terz. Sie bestand aus zwei Ganztönen und errechnete sich folglich aus:
8 8 64
× =
9 9 81
Entsprechend einer solch schwierigen Proportion, klang auch die Terz sehr „imperfekt“.
Um die Zeitenwende (ca. 30 v.Chr.) gelang es dem Griechen Didymos von Samos, das pythagoräische
System zu verbessern, indem er die Terzen verbesserte: Die große Terz wurde auf 4:5, die kleine Terz
auf 5:6 gelegt. Daraus wurde die sogenannte Reine Stimmung (auch natürlich-harmonische Stimmung
genannt). Sie beruht darauf, dass der gewohnte Ganzton 8:9 differenziert wird: Es gibt einen großen
Ganzton (8:9) und einen kleinen Ganzton (9:10). Die große Terz 4:5, die sich aus zwei Ganztönen
zusammensetzt, errechnet sich aus: 8:9 x 9:10 = 72:90 = 4:5.
Zudem wurde das Limma durch den Halbton mit 16:15 ersetzt.
- 18 -
Aus einer Intervallfolge von 5 Ganztönen und 2 Limma wurde: 3 große Ganztöne, 2 kleine Ganztöne
und 2 Halbtöne. Es ergab sich eine Intervallfolge:
9 10 16 9 10 9 16 18662400 2
× × × × × ×
=
=
8
9 15 8 9 8 15
9331200
1
Die Tonleiter konnte also sauber mit rationalen Zahlen gerechnet werden, ergab wohlklingende
Terzen bzw. Sexten und konnte auf das komplizierte Limma verzichten. Das Ergebnis wird bis heute
auch als diatonische Leiter bezeichnet. 10
Die einzelnen Töne standen in der folgenden Proportion zueinander:
24 : 27 : 30 : 32 : 36 : 40 : 45 : 48 Mit den einzelnen Faktoren formuliert, heißt es:
𝟐𝟒 F
G
𝟐𝟕 BI
F
𝟑𝟎 B<
BK
𝟑𝟐 F
G
𝟑𝟔 BI
F
𝟒𝟎 F
G
𝟒𝟓 B<
BK
𝟒𝟖
Um die ganzzahlig fortlaufende Proportion graphisch zu veranschaulichen, müssen wir aus den oben
beschrieben 12 gleichen Teilen einer Saite 48 machen. Jeder Teil muss also zusätzlich geviertelt
werden, denn 12×4 = 48. Das diatonische Stimmungsschema zeigt sich in Abbildung 8:
Zum Vergleich: In der Pythagoräischen Teilung lautete die ganzzahlig fortlaufende Proportion:
384 : 432 : 486 : 512 : 576 : 648 : 729 : 768 Sie war also wesentlich komplizierter. Die Zusammenhänge werden in E. SCHRÖDER, Mathematik im
Reich der Töne (Frankfurt am Main 1985) sehr anschaulich beschrieben. Vgl. Kapitel 7: Monochord und
Kapitel 8: Diatonisches Stimmungsprinzip.
10
- 19 -
Abbildung 8: Diatonische Proportion an der 48-fach geteilten Seite. Oben die Frequenzverhältnisse – unten die
Teilungsverhältnisse. (Entlang der Punktlinie zeigen sich die Komplementärintervalle.)
Durch die so vorgenommenen Anpassungen gaben sich mehrere Vorteile beim Musizieren: Erstens
war das Limma mit seinem komplizierten Verhältnis verschwunden und zweitens wurden die Terzen
günstiger (vgl. 64:81 mit 5:4 bzw. 6:5).
Wir sind nun den Weg von den ersten Saitenteilungen der Pythagoräer bis zu den diatonischen
Leitern gegangen. Mit diesen Leitern musizieren unsere Musiker bis heute. Es wurde klar, dass die
Zahlen 7 und 12 dabei eine Schlüsselrolle spielen. 7 das ist die Zahl der Töne in einer Leiter bis wieder
derselbe Ton an achter Stelle eintritt. 12 das ist die Zahl der chromatischen Teilungen einer Oktave.
Soweit nun die Entwicklung der Musiktheorie. Nun bietet es sich an, die Schemen der Musiktheorie
mit denen der Anatomie zu vergleichen.
- 20 -
4. Die Schemen im Vergleich
Bei Betrachtung der Schemen des menschlichen Brustkorbes und der Musik des Westens entstehen
deutliche Übereinstimmungen.
1. Der Oktavraum gliedert sich in 12 Halbtöne, wobei derer 7 zu einer Tonleiter zusammengefasst
werden | Der menschliche Brustkorb gliedert sich in 12 Rippenpaare, wobei derer 7 fest an das
Sternum gewachsen sind.
Musik
Anatomie
12 chromatische Töne innerhalb der
12 Rippenpaare innerhalb des Brustkorbes
Oktave
7 dieser chromatischen Töne bilden eine
7 dieser Rippenpaare sind fest mit dem
diatonische Leiter.
Brustbein verwachsen (Fachbegriff ‚echte’
Rippen).
12 Quinten ergeben gerundet 7 Oktaven
(Beachte: Spiralbewegung nicht
Kreisbewegung)
2. Die 12 Halbtöne der Oktave gehorchen der Teilung in Quinte und Quarte: 7 Halbtöne gehen
auf die Quinte – 5 auf die Quarte. Im Schema gilt 12 = 7 + 5. | Die 12 rippenlosen Wirbel
gehorchen dem Schema 12 = 7 + 5, denn 7 von ihnen sind Halswirbel und 5 von ihnen sind
Lendenwirbel. | Die berippten Wirbel gehorchen ebenfalls diesem Schema, denn 7
Rippenpaare sind echt, fünf sind unecht.
Musik
Anatomie
Oktave = Quinte + Quarte
Brustkorb = echte Rippen + unechte Rippen
12 Halbtöne = 7 Halbtöne + 5 Halbtöne
12 unberippte Wirbel = 7 Halswirbel + 5
Lendenwirbel
3. Die westliche Musik kennt 24 Tonarten, die eigentlich 12 Tonartenpaare sind (C-Dur = A-Moll)
| Der menschliche Brustkorb besteht aus 24 Rippen, die eigentlich 12 Rippenpaare sind.
Die westliche Musik arbeitet mit 12 Dur-
Die Wirbelsäule arbeitet mit 12 berippten
Tonarten und 12 Moll-Tonarten. Die Summe
und 12 unberippten Wirbeln. Die Summe ist
beträgt 24.
24.
Der Brustkorb arbeitet mit 12 linken Rippen
und mit 12 rechten Rippen. Die Summe ist
24.
- 21 -
Nun kann man sich fragen, ob es überhaupt sinnvoll ist, ein natürliches Phänomen – unsere Anatomie,
mit einem kulturellen Phänomen – unserer Musiktheorie, zu vergleichen. Unsere Anatomie ist eine
natürliche Gegebenheit, auf die wir Menschen keinen Einfluss haben und die Musik, das ist eine
kulturelle Sache, die wir Menschen sehr wohl mitbestimmen. Kann man diese Dinge also wirklich
sinnvoll vergleichen? Um diese Frage zu klären, lohnt es nach Musiktheorie zu fragen, die völlig
außerhalb unseres europäischen Kulturkreises entstanden ist.
5. Zwischenbetrachtung: Der Weg der Altchinesischen Musik
Werfen wir einen Blick auf die Musiktheorie des Alten Chinas. Wie in vielen anderen Kulturfragen haben
die Chinesen bereits vor vielen Jahrhunderten ihre eigenen Grundsteine gelegt und darauf gebaut. Hier
zeigt sich Verblüffendes: Bereits zur Shang-Dynastie (ca. 1500-1000 v.Chr.) – also lange vor der
griechischen Klassik, musizierten die Vorfahren der heutigen Chinesen auf dem Tonsystem der
sogenannten "12 Lü". Im dtv-Atlas Musik lesen wir zum Thema:
"Shang-Dynastie (ca. 1500-1000)
Dem Tonsystem liegen die 12 Lü (Halbtöne) zu Grunde, die sich aus der Folge reiner Quinten
herleiten. Ein Ausschnitt von 5 Quinten liefert jeweils das Material für eine pentatonische Leiter.
Jeder der 5 Töne kann Grundton der Leiter sein, sodass sich je Leiter 5 Tonarten ergeben. Da
die pentatonische Leiter auf jedem der 12 Lü aufgebaut werden kann, kommt man auf 60
Tonarten.
Chou Dynastie (ca. 1000-256)
(...) Das System der relativen 12 Lü blieb bestehen, wurde jedoch spätestens um 300 v. Chr.
durch heptatonische Leitern erweitert. (...) Die heptatonische Musik gilt als neu." 11
Es zeigt sich aber mit Klarheit, dass sich im Altchinesischen Reich ein 12-Halbtonsystem einspielte.
Außerdem fällt der Übergang von pentatonischen Leitern zu heptatonischen auf. Die 60 Tonarten des
pentatonischen Musizierens errechnen sich aus 12×5; die 84 Tonarten des heptatonischen Musizierens
errechnen sich aus 12×7.
Zitierenswert ist hier eine Anmerkung, die R. AMON im Kapitel zum Quintenzirkel schreibt:
„Als nachweislich erster hat Aristoxenos von Tarent (ca. 360-300 v.Chr.), Schüler von Aristoteles,
Philosoph und Musiktheoretiker, ein Quintverfahren angewandt. Von ihm stammen die
Bezeichnungen Ganzton und Halbton. Er definiert die Quint als summe von Quart plus Ganzton,
die Quart entsprechend als Summe von Ganzton plus Ganzton plus Halbton.
Fast zeitgleich hat in China Lü Pu We(i) (gest. 295 v.Chr.) im Buch „Frühling und Herbst“ den
Mythos um die Entstehung der „Zwölf Lü“ – einer Rechenregel, die mit unserem Quintenzirkels
faktisch identisch ist (jedoch nach einem anderem Prinzip gewonnen) – dargestellt. Ab der
Renaissance (...) erfolgt im Abendland eine intensive Auseinandersetzung mit dieser Materie.“12
Trotz aller Unterschiede der Kulturkreise, die bis heute bestehen, zeigen sich Gemeinsamkeiten
11
12
Michels: dtv-Atlas Musik, S.169
Amon: Lexikon der Harmonielehre, S.218
- 22 -
zwischen europäischer und altchinesischer Musiktheorie: Die Schlüsselrolle der Zahl 12 findet sich in
beiden Erdteilen und auch der Übergang vom pentatonischen System zum heptatonischen zeigt die
Bedeutung der Ziffern 5 und 7. Wie kann dies sein, da beide Musiksysteme unabhängig voneinander
entstanden sind? Vielleicht liegt der Grund hierfür weniger im Zufall, denn in natürlichen
Rahmenbedingungen. Denken wir an die 7. Durch Verwendung von Siebentonleitern können Oktaven
durch 5 Ganztonschritte und 2 Halbtonschritte rechnerisch sauber überwunden werden. Durch 5 weitere
Halbtone in der Oktave, kann auf jedem Ton der Leiter eine eigene Leiter gebaut werden: Auf der Prim
ist eine Tonleiter möglich (C-Dur), auf der Sekunde ist eine Tonleiter möglich (D-Dur), auf der Terz ist
eine Tonleiter möglich (E-Dur) und so weiter bis wir bei der Septime angelangen (H-Dur). Hier brauchen
wir alle zusätzlichen Halbtöne, die nichts anderes sind, als die schwarzen Tasten – denn natürlich hat ein
Klavier bis heute 7 weiße und 5 schwarze Tasten innerhalb einer Oktave. Die Zwölftelung der Oktave
bietet zudem den Vorteil, dass die Halbtöne nicht nach dem Modus „Dur“ angeordnet werden müssen,
es kann auch im Modus „Moll“ erfolgen. Die Leiter kann als Ganzton-Ganzton-Halbton oder HalbtonGanzton-Ganzton etc. interpretiert werden. Zuletzt kann man noch daran erinnern, dass die Teilung
einer Saite in 12 Teile alle konsonanten Intervalle (Quinte, Quarte, Oktave, Duodezime und
Doppeloktave) darstellt.
Es zeigt sich also, dass die Besonderheit dieser Zahlen nicht aus Zahlenmystik oder der
Geheimniskrämerei des Pythagoras hervorgegangen ist. Hinter ihr stehen mitunter rechnerische
Gründe, deren Folgen sich bis heute im Phänotyp der Musiktheorie zeigen. Auch die Theorie des letzten
Jahrhunderts konnte sich nicht von ihr lösen. Als bestes Beispiel mag hier Arnold Schönbergs Vision
einer atonalen Musik dienen: Obwohl er die Arbeit mit diatonischen Leitern aufgab, blieb die
Bedeutung der Zahl 12 in seiner Zwölftonmusik eindeutig bestehen.
Kehren wir im letzten Kapitel zu Pythagoras und seiner Geheimniskrämerei zurück. Die Bedeutung, die
er den Zahlen 1 bis 4 beimaß, wurde oben bereits angesprochen. Nun kann man sich fragen, warum sie
ihm gar als heilig galten. Die wahrscheinlich banalste Erklärung liegt darin, dass die Summe der Zahlen
von 1 bis 4 gleich 10 ist und da jeder Mensch 10 Finger haben sollte, musste es etwas besonderes mit
diesen Zahlen auf sich haben.
1 + 2 + 3 + 4 = 10
Doch geht die Bedeutung dieser Zahlen, wie wir gelernt haben, weiter als es im ersten Augenblick
scheint. Vor allem die Verhältnisse, die sich aus ihnen ergeben, sind von tieferer Bedeutung.
Abbildung 9: Die 10 als sog. Dreieckszahl: Die Menge einer Dreieckszahl lässt sich als gleichseitiges Dreieck anordnen. Z.B. 3, 5
,10 ,15 etc.
- 23 -
6. Geometrische Grundkörper und musikalische Verhältnisse
Das Leben des wahrscheinlich begabtesten Mathematikers der Antike – Archimedes von Syrakus (ca.
287 - 212 v.Chr.) ist legendenumwoben. Als er aus dem Bade stieg soll er "Heureka, heureka" gerufen
haben und sei gar nackt nachhause geeilt. Vor seinem Tod durch das Schwert eines römischen Soldaten,
lauteten seine letzten Worte: "Störe meine Kreise nicht!" – so sagt es die Legende. Weniger berühmt,
aber genauso bemerkenswert ist das Grab, in dem er angeblich beigesetzt worden sei. Es hatte die
Form einer Kugel, die von einem Zylinder umschlossen ist. Was wollte uns Archimedes über die Sprache
dieser Architektur übermitteln?
Zu jeder Kugel existiert ein Zylinder, der sie genau einschließt. Der Grundkreis dieses Zylinders gleicht
dem Inkreis der Kugel, die Höhe des Zylinders gleicht dem Kugeldurchmesser, also dem doppelten
Radius.
Aus dem Schulunterricht wissen wir, dass sich der Inhalt einer Kugel nach der Formel 𝑉 = 4 3 𝑟 A 𝜋
errechnen lässt. Wie können wir uns dieses Produkt körperlich vorstellen? Die Faktoren 𝑟 A 𝜋 können wir
als 𝑟 6 𝜋 × 𝑟 umformen und körperlich beschreibt 𝑟 6 𝜋 × 𝑟 einen Zylinder: Seine Grundfläche ist 𝑟 6 𝜋, seine
Höhe ist 𝑟. Da sich das Volumen eines Zylinder aus der Grundkreisfläche multipliziert mit der Höhe
ergibt, erhalten wir die Formel 𝑟 6 𝜋 × 𝑟.
Abbildung 10: Die Höhe des halben Zylinders entspricht dem Radius, die Höhe des ganzen Zylinder entsrpicht dem
Durchmesser der Kugel.
Dieser Zylinder reicht genau bis zum Äquator unserer Einheitskugel, denn er ist halb so hoch wie oben
beschriebener Umfassungszylinder, dessen Höhe dem Durchmesser gleicht. Dieser errechnet sich aus
Grundkreisfläche (𝑟 6 𝜋) multipliziert mit der Höhe (2𝑟), also als 𝑟 6 𝜋 × 2𝑟.
Nun besagt die Formel als 𝑉 = 4/3𝑟 A 𝜋 , dass der Inhalt der Einheitskugel um 4/3 größer ist, als ihr
Halbzylinder mit Inhalt 𝑟 A 𝜋. Die Einheitskugel ist also eine Quarte größer als ihr Halbzylinder.
Wie verhält sich nun der Vollzylinder zur Kugel? Das Vollzylindervolumen errechnet sich aus 2𝑟 × 𝑟 6 𝜋 =
2𝑟 A 𝜋 (Höhe mal Grundkreisfläche).
Nun können wir den Kugelinhalt 4/3𝑟 A 𝜋 ins Verhältnis zum Vollzylinderinhalt 2𝑟 A 𝜋 setzen:
2𝑟 A 𝜋
4 A
𝑟 𝜋
3 Nach dem Kürzen bleibt:
- 24 -
2 3
=
4 2
3
Dies ergibt 3:2 – also den Quotient der Quinte. Folglich entspricht der Inhalt des Umfassungszylinders
dem eineinhalbfachen Kugelinhalt. Er ist um eine Quinte größer als die Einheitskugel.
Zusammenfassend lässt sich sagen:
• Der Inhalt der Einheitskugel ist 4 3 größer, als der ihres Halbzylinders. Die Einheitskugel ist
also eine Quarte größer, als ihr Halbzylinder.
• Der Inhalt des Umfassungszylinders ist um 3 2 größer, als der der Einheitskugel. Er ist also
eine Quinte über der Einheitskugel.
• In den Verhältniszahlen 4 3 und 3 2 sind Quarte und Quinte geometrisch verewigt. Ihr
Produkt 4/3 × 3 2 ergibt 12 6 also 2 1. Und 2 1 entspricht wieder der Oktavzahl 2.
Eine Kugel und ihr Umfassungszylinder lehren uns also die Bedeutung von Quinte und Quarte: Der
Kugeläquator halbiert den Umfassungszylinder, jedoch ist die Kugel eine Quarte größer als der
Halbzylinder. Der Vollzylinder ist wiederum eine Quinte größer als die Einheitskugel.
𝑉𝑜𝑙𝑢𝑚𝑒𝑛 𝐻𝑎𝑙𝑏𝑧𝑦𝑙𝑖𝑛𝑑𝑒𝑟
]^_`ab
𝑉𝑜𝑙𝑢𝑚𝑒𝑛 𝐸𝑖𝑛ℎ𝑒𝑖𝑡𝑠𝑘𝑢𝑔𝑒𝑙
𝑉𝑜𝑙𝑢𝑚𝑒𝑛 𝐻𝑎𝑙𝑏𝑧𝑦𝑙𝑖𝑛𝑑𝑒𝑟
kla_mb
]^ijab
𝑉𝑜𝑙𝑢𝑚𝑒𝑛 (𝑉𝑜𝑙𝑙𝑧𝑦𝑙𝑖𝑛𝑑𝑒𝑟)
𝑉𝑜𝑙𝑢𝑚𝑒𝑛 (𝑉𝑜𝑙𝑙𝑧𝑦𝑙𝑖𝑛𝑑𝑒𝑟)
Das Volumenverhältnis von Kugel und Umfassungszylinder war von Archimedes entdeckt worden und
dieses Wissen sollte offenbar für die Nachwelt in architektonischer Weise konserviert werden.13
Betrachten wir nun die Oberfläche einer Kugel. Sie errechnet sich nach der Formel 4𝑟 6 𝜋. Wir haben es
also mit dem Inkreis der Kugel 𝑟 6 𝜋 und dem Faktor 4 zu tun. Die Oberfläche einer Kugel ist viermal
größer als ihr Inkreis. Oder umgekehrt: Die Fläche des Inkreises einer Kugel beträgt 1 4 der
Kugeloberfläche. Im Faktor 1 4 erkennen wir klar die Doppeloktave.
𝐹𝑙ä𝑐ℎ𝑒 𝐼𝑛𝑘𝑟𝑒𝑖𝑠
rsttbusla_mb
𝑂𝑏𝑒𝑟𝑓𝑙ä𝑐ℎ𝑒 𝐾𝑢𝑔𝑒𝑙
Abbildung 11
Diese Betrachtungen können bei anderen geometrischen Körpern weiterverfolgt werden: Betrachten
wir nun den Kegel. Sein Volumen berechnet sich nach der Formel 𝑉 = 1 3 ℎ𝑟 6 𝜋. Auch hier hat man es
mit einem Umfassungszylinder zu tun. Er wird durch Grundkreis und Höhe des Kegels beschrieben.
13
Zum Grab des Archimedes vlg. Dilke: Mathematik, Maße und Gewichte in der Antike, S.37
- 25 -
Abbildung 12
Nach obiger Formel sind Kegel und Umfassungszylinder proportional. Sie stehen im Verhältnis 1 3. Der
Umfassungszylinder ist im Volumen dreimal größer als der Kegel. Da 1 3 das Verhältnis der Duodezime
ist, können wir folgern, dass jeder Umfassungszylinder eine Duodezime größer ist als der Kegel, den er
umfasst.
𝑉𝑜𝑙𝑢𝑚𝑒𝑛 𝐾𝑒𝑔𝑒𝑙
r^sybzi{b
𝑉𝑜𝑙𝑢𝑚𝑒𝑛 (𝑈𝑚𝑓𝑎𝑠𝑠𝑢𝑛𝑔𝑠𝑧𝑦𝑙𝑖𝑛𝑑𝑒𝑟)
Gleiches gilt für die Pyramide. Jede Pyramide kann durch einen Quader (Grundfläche mal Höhe)
beschrieben werden. Das Pyramidenvolumen beträgt 1 3 ihres Umfassungsquaders.
𝑉𝑜𝑙𝑢𝑚𝑒𝑛 𝑃𝑦𝑟𝑎𝑚𝑖𝑑𝑒
r^sybzi{b
𝑉𝑜𝑙𝑢𝑚𝑒𝑛 (𝑈𝑚𝑓𝑎𝑠𝑠𝑢𝑛𝑔𝑠𝑞𝑢𝑎𝑑𝑒𝑟)
Wir sehen also, dass sich die sog. „konsonanten“ Intervalle auch in den geometrischen Grundkörpern
finden. Sie zeigen sich aber auch in einfachen Figuren, wie dem Dreieck: Jedes geradlinige Dreieck
kann von einem Rechteck (𝑎×ℎ) umschrieben werden. Die Dreiecksfläche berechnet sich mit 1/2𝑎ℎ.
Somit ist das Umfassungsrechteck eine Oktave größer als das Dreieck.
𝐹𝑙ä𝑐ℎ𝑒 𝐷𝑟𝑒𝑖𝑒𝑐𝑘
kla_mb
𝐹𝑙ä𝑐ℎ𝑒 (𝑈𝑚𝑓𝑎𝑠𝑠𝑢𝑛𝑔𝑠𝑟𝑒𝑐ℎ𝑡𝑒𝑐𝑘)
Abbildung 13
Es zeigt sich also mit Klarheit, dass in den geometrischen Figuren und Körpern die pythagoräischen
Verhältnisse verewigt sind:
• Die Oktave zeigt sich im Dreieck mit seinem Umfassungsrechteck.
• Quarte und Quinte zeigen sich in der Kugel und ihrem Halb- bzw. Vollzylinder.
• Die Duodezime zeigt sich im Kegel und seinem Umfassungszylinder. Gleiches gilt für die
Pyramide und ihren Umfassungsquader.
- 26 -
• Die Doppeloktave zeigt sich in der Kugeloberfläche, die der vierfachen Inkreisfläche entspricht.
Die Verhältnisse die zum Einsatz kommen sind:
𝟏 𝟐
𝟐 𝟑
𝟑 𝟒
𝟏 𝟑
𝟏 𝟒
𝟐 𝟏
𝟑 𝟐
𝟒 𝟑
𝟑 𝟏
𝟒 𝟏
oder
In der Musik liefern sie die perfekten Konsonanzen Oktave, Quarte, Quinte, Duodezime, Doppeloktave.
Die natürlichen Zahlen, die für diese Verhältnisse angewandt werden sind: 1, 2, 3, 4
Abschließend soll noch erwähnt werden, dass die Verhältnisse der Tetraktis auch in der Berechnung von
Parabelsegmenten erscheinen. Hier schließt sich der Kreis zu Archimedes: Zu jedem Parabelsegment
zwischen zwei Punkten B und C, gibt es ein kennzeichnendes Dreieck aus der Grundlinie BC und dem
Punkt A, der auf der parallelen Tangente zu BC liegt.
Abbildung 14
Archimedes behauptete der Flächeninhalt des Parabelsegmentes verhalte sich zur Dreiecksfläche wie
4:3. Was veranlasste ihn zu dieser Behauptung? Archimedes erkannte, dass zwischen Dreieck ABC und
dem Parabelsegment zwei Restflächen bestehen bleiben, die wiederum Parabelsegmente sind. Also
konnte er die angewandte Methode wiederholen und zwei neue Dreiecke in den Restflächen definieren.
Das sind die Dreiecke BGA und CHA. Er erkannte, dass die Flächen der beiden kleinen Dreiecke nur
ein Viertel des großen Dreiecks betragen. Die näherungsweise Fläche des großen Parabelsegments
beträgt also
1 + 1/4
der Dreiecksfläche ABC. Wiederholt Archimedes seine Methode, so werden die Dreiecke der dritten
Generation nur noch 1/16 des Urdreiecks betragen. Die Dreiecke der vierten Generation werden 1/64
betragen und so fort. Nichts außer seiner endlichen Lebenszeit vermag nun Archimedes daran hindern,
diese Methode unendlich zu wiederholen. Durch unendliche Generationen von Dreiecken entsteht eine
Summe von Brüchen, die sich dem Wert 4/3 annähert:
1+
1
1
1
1
4
+
+
+
+⋯=
4 64 256 1024
3
- 27 -
Obwohl Archimedes nicht von Unendlichkeit sprach, erkannte er dennoch, dass er mit dieser Methode
den Parabelinhalt erschöpfend beschreiben konnte. 14
Dies bedeutet, dass Parabelsegment und Dreieck in einem rationalen Verhältnis stehen: Das
Parabelsegment ist eine Quarte größer als das Dreieck aus den Segmentpunkten und dem Punkt der
Paralleltangente.
14
vgl. Taschner: Das Unendliche. Mathematiker ringen um einen Begriff, S. 37 ff.
- 28 -
C. Schluss
Ziel dieser Arbeit war es, die Schnittmengen zwischen Anatomie, Musik und Geometrie darzustellen.
Wir haben die menschliche Wirbelsäule und den Brustkorb im Schema betrachtet. Daneben haben wir
die Grundlagen der Musiktheorie gelegt. Im Vergleich der Schemen zeigten sich Übereinstimmungen.
Nach einem Blick auf die Musiktheorie des alten Chinas bestätigten sich diese Hinweise.
Zuletzt wurden die geometrischen Grundkörper beleuchtet und deren Verhältniszahlen hervorgehoben.
Auch hier zeigen sich deutliche Übereinstimmungen zur Musiktheorie der Pythagoräer. Wir wissen nicht,
inwieweit diese die Volumenverhältnisse von Kugeln, Zylindern und Kegeln errechnen konnten. Das
Volumenverhältnis von Kugel und Zylinder geht auf Archimedes zurück, der Jahrhunderte nach
Pythagoras lebte. Auch gilt es zu hinterfragen, wie weit Pythagoras’ Kenntnisse der Zahl 𝜋
fortgeschritten waren. Heute wissen wir, dass es sich unzweifelhaft um eine irrationale Zahl handelt, also
keine Zahl, die sich je durch einen Bruch ohne Rundung darstellen lassen wird. Wir wissen auch, dass
Pythagoras die Vorstellung irrationaler Zahlen (z.B.
2) vehement ablehnte. Also dürfte er die Zahl 𝜋
durch einen Rundungswert ersetzt haben – was wir bis heute tun. Wir betrachten 𝜋 als eine Unbekannte
in unseren Gleichungen die wir, je nach Erfordernis durch einen Rundungswert (z.B. 3,14) ersetzen.
Sicher ist, dass Pythagoras einer der ersten war, der lehrte, die Erde sei eine Kugel. Eine Einsicht, die
sich später bestätigen sollte und über Jahrhunderte nur wenigen Gelehrten vorbehalten war. Die
Proportionen, die er festlegte und als konsonant bezeichnete, leben darüber hinaus in den
geometrischen Grundkörpern auf ewig weiter. Neben der Wiederkehr seiner Verhältniszahlen, lag ein
Teil dieser Arbeit auf den Zahlen 7 und 12. Sie gelten seit jeher als „magisch“, doch wird deren Magie
zumeist mythisch oder religiös erläutert. Man liest von den 7 Planeten und den 12 Sternbildern der
Antike, oder es ist die Rede von den 7 Schöpfungstagen, den 7 Jahren in Josefs Traumdeutung, den 12
Stämmen Israels oder den 12 Aposteln.15 Diese Begründung ist kulturhistorisch korrekt, doch sollte
diese Arbeit zeigen, dass auch im naturwissenschaftlichen Bereich die 7 und die 12 eine besondere
Rolle einnehmen. 7 als die Zahl der Halswirbel oder der sternalen Rippenpaare. 12 als die Zahl der
Brustwirbel oder die Anzahl der rippenlosen Wirbel. Diese Besonderheit zeigt sich gleichermaßen in
der Musiktheorie, wo 7 die Zahl der diatonischen Leitern und die 12 die Zahl der chromatischen Leitern
darstellt. In 12 Segmente teile Pythagoras auch seine Monochordsaite und damit blieb er nicht allein:
Auch die alten Römer machten die Vorteile der 12 im praktischen Leben zu nutze. Das Zwölftel heißt
auf Latein nämlich uncia und mit solchen „Unzen“ wurden die Hebelwaagen der Geschäftsleute (lat.
libra) bedient. Dabei galt:
12 uncia = 1 libra
Auch im Münzwesen waren Unzen gebräuchlich. Hier ergaben 12 Unzen 1 As.16
Der praktische Grund hinter Zwölfteln liegt in der Teilbarkeit der Zahl. 12 kann ohne Rest durch 1,2, 3,
4 und 6 geteilt werden. Natürlich kann 12 auch durch 12 geteilt werden – doch gilt dies an und für sich
für jede Zahl. Wir können also die echten Teiler der 12 addieren und erhalten:
s(12) = 1 + 2 + 3 + 4 + 6 = 16
15
16
vgl. Haarmann: Weltgeschichte der Zahlen, S.24 f und S. 29 f
Dilke: Mathematik, Maße und Gewichte in der Antike, S.90 ff und S.103
- 29 -
Damit ist die Summe der echten Teiler größer als die 12 selbst. In der Zahlentheorie heißt sie deshalb
„abundante Zahl“. Wäre die Teilersumme kleiner 12, hieße die Zahl „defizient“. Wäre sie gleich 12, so
hieße die Zahl „vollkommen“. Da 12 abundant (also teilerreich) ist, können Massen oder Beträge gut
dividiert werden. Ein Kaufmann kann jederzeit ein As teilen und ein Halbes, ein Drittel, ein Viertel oder
ein Sechstel an einen Geschäftspartner ausgeben – zum Beispiel als Vorschuss, als Kredit oder Rendite.
Dieser Gedanke zeigt sich bis heute in den USA, wo der quarter als Vierteldollar-Münze im Umlauf ist.
Auch Gewichte konnten so praktisch geteilt werden.
Bekanntermaßen hat die 12 als Ordnungszahl die Jahrhunderte nicht überdauert. Wir modernen
Kontinent-Europäer denken im metrischen System – einer Erfindung der Französischen Revolution. Mit
dem System kam auch die 10 als einzige Ordnungszahl. Seither sind 10 mal 10 mal 10 Meter ein
Kilometer. Und 10 Meter mal 10 Meter mal 10 Meter sind 1000 Kubikmeter. Und ein Kubikmeter fasst
1000 Liter Wasser und 1000 Liter Wasser wiegen 1000 Kilogramm. Folglich wiegen 1000 Kubikmeter
Wasser 1000 mal 1000 Kilogramm und so fort. Die Intellektuellen der Französischen Revolution (die
„Dekadisten“) gingen in ihrer Vernunft-Religion sogar soweit, das Jahr, den Monat, den Tag und die
Stunde nach der 10 zu ordnen. Doch so gut sich ihre Vorschläge bei der Vermessung des Raumes
durchsetzten, so schlecht wurden sie bei der Vermessung der Zeit angenommen.17 Ein rationaler Grund
hierfür liegt an der Natur der 10. Zwar ist sie die Summe der ersten vier Zahlen, doch ist sie auch eine
defiziente Zahl. Sie lässt sich nur durch 2 und 5 teilen. Die Summe der echten Teiler lautet nämlich:
s(10) = 1 + 2 + 5 = 8
Wäre zum Beispiel unser Jahr nach 10 Revolutionsmonaten aufgeteilt, wären uns nur das Halbjahr, das
Fünfteljahr und das Zehnteljahr vertraut. Das Vierteljahr (Quartal) und das Dritteljahr wären uns kein
Begriff. Gleiches gälte für die Stunde: Unbekannt wäre die Viertelstunde und natürlich auch die
Dreiviertelstunde etc.
Es zeigen sich also auch Nachteile des dekadischen Systems. Historisch gesehen setzte sich das
metrische System beinahe global durch – der Revolutionskalender hingegen wurde noch unter
Napoleon Bonaparte aufgegeben. Da die Briten diesen kontinentalen Umtrieb immer skeptisch sahen,
haben sie sich bis heute ihre ounzes als Gewichtsmaß erhalten. Unlogischerweise gilt:
16 ounces = 1 pound
Zum Abschluss des Textes noch eine kleine Rätselfrage:
Wie kann man allein mit einem Seil einen Rechten Winkel schlagen?
17
vgl. Beutelspacher: Zahlen: Geschichte, Gesetze, Geheimnisse, S.77
- 30 -
Die Lösung erfolgt über ein pythagoräisches Dreieck. Für seine Seiten gilt immer:
𝑎 6 + 𝑏 6 = 𝑐 6
Bei diesem Seitenverhältnis ist der Rechte Winkel an den Katheten garantiert. Das kleinste dieser
Dreiecke besteht aus dem Zahlentrio 3;4;5, denn
36 + 46 = 56 .
Interessant ist nun, dass die Summe dieser Seitenlängen 12 ergibt, denn
3 + 4 + 5 = 12 .
Wird also ein Seil mit der Länge 1 in zwölf gleiche Segmente geteilt, so kann daraus ein Rechter Winkel
geschlagen werden. Man gebe 5 Segmente auf die Hypotenuse und 7 auf die Katheten. Es ergibt sich
ein Dreieck mit den Saitenlängen 3,4 und 5. Dieses schließt einen Rechten Winkel ein. Dazu muss man
das Seil aber in 12 gleiche Segmente teilen – wie es eben Pythagoras auch mit der Saite tat, um die
konsonanten Intervalle zu finden.
- 31 -
D. Literaturverzeichnis
Amon, Reinhard: Lexikon der Harmonielehre (Wien 2005).
Beutelspacher, Albrecht: Zahlen. Geschichte, Gesetze, Geheimnisse (München 2015).
Dilke, O.A.W.: Mathematik, Maße und Gewichte in der Antike; Reclam Sachbuch (Stuttgart 2012).
Haarmann, Harald: Weltgeschichte der Zahlen (München 2008).
Heuser, Harro: Die Magie der Zahlen. Von der seltsamen Lust, die Welt zu ordnen (Freiburg i.Br. 2003).
Holst, Immogen: Das ABC der Musik (Stuttgart 2009).
Johnen, Kurt: Allgemeine Musiklehre (Stuttgart 2008).
Kanitscheider, Bernulf: Natur und Zahl (Heidelberg 2013).
Keil, Werner: Musikgeschichte im Überblick (Paderborn 2012).
König/Liebich: Anatomie der Haussäuger (Stuttgart 2015).
Martini/Timmons/Tallitsch: Anatomie (München 2012).
Michels, Ulrich: dtv-Atlas Musik (München 2001).
Nestler, Gerhard: Geschichte der Musik (Gütersloh 1997).
Netter, Frank H.: Farbatlanten der Medizin. Band 7 - Bewegungsapparat I (Stuttgart 1992).
Riedweg, Christoph: Pythagoras. Leben, Lehre, Nachwirkung (München 2002).
Schneider, Ivo: Archimedes. Ingenieur, Naturwissenschaftler, Mathematiker (Berlin/Heidelberg 2016).
Schröder, Eberhard: Mathematik im Reich der Töne (Frankfurt am Main 1985).
Taschner, Rudolf: Das Unendliche. Mathematiker ringen um einen Begriff (Berlin/Heidelberg 2006).
Waschke/Böckers/Paulsen: Anatomie – das Lehrbuch (München 2015).
- 32 -
33