Wohltemperiert in guter Stimmung

1
Wohltemperiert in guter Stimmung
Grundlagen zu Mathematik und Musik
Johannes B. Huber
Weshalb klingen Oktaven völlig rein und können Quinten
beim Stimmen von Streichinstrumenten absolut richtig austariert werden? Weshalb werden kleine Sekunden oder das
Drei–Ganzton–Intervall (Tritonus) in der Musik als Dissonanzen wahrgenommen? Sind das nur subjektive, beim Hören
abendländischer Musik erlernte Empfindungen oder stecken
dahinter allgemeine Prinzipien? In diesem Beitrag soll verdeutlicht werden, dass anhand der natürlichen Obertonreihe
mathematisch begründet ist, weshalb wir Intervalle musikalisch als konsonant oder dissonant empfinden, weshalb Dur–
und Moll–Tonleiter gerade so sind, wie sie heute gebräuchlich
sind und weshalb im Laufe der Musikgeschichte die Oktave
in 12 Halbtonschritte eingeteilt wurde. Die Obertonreihe ist
jedoch mit unserer Empfindung der Tonhöhe als Logarithmus
der Schwingungsfrequenz nicht in Einklang zu bringen, was
dazu führt, dass ein widerspruchsfreies musikalisches Stimmungssystem nicht existieren kann. Einige historische Kompromissvorschläge zur Stimmung von (Tasten–)Instrumenten
werden vorgestellt und verglichen.
II. F OURIER –A NALYSE VON T ÖNEN , KONSONANZ UND
D ISSONANZ
Diese Reihenentwicklung hat insofern grundsätzliche Bedeutung, dass einerseits durch unseren Gehörsinn eine solche
Zerlegung tatsächlich stattfindet, denn unser Gehör wirkt als
Kurzzeit–Spektral–Analysator. Andererseits ergibt die Überlagerung von unterschiedlich großen und wechselseitig verschobenen Cosinus–Schwingungen (z.B. durch Zeitverzögerung, vgl. Reflexionen von Schallwellen in halligen Räumen)
gleicher Frequenz aufgrund der Additionstheoreme der Trigonometrie wieder eine Cosinus–Schwingung dieser Frequenz.
(Mathematisch ausgedrückt bedeutet dies, dass Cosinus–
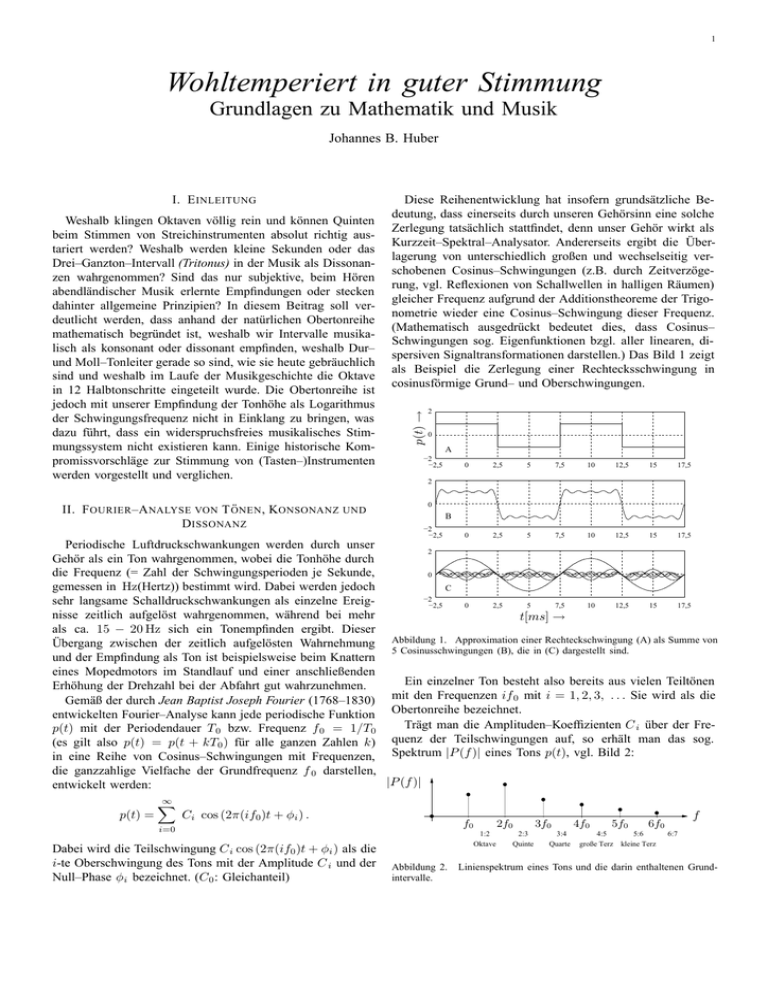
Schwingungen sog. Eigenfunktionen bzgl. aller linearen, dispersiven Signaltransformationen darstellen.) Das Bild 1 zeigt
als Beispiel die Zerlegung einer Rechtecksschwingung in
cosinusförmige Grund– und Oberschwingungen.
p(t) →
I. E INLEITUNG
2
0
A
−2
−2,5
0
2,5
5
7,5
10
12,5
15
17,5
0
2,5
5
7,5
10
12,5
15
17,5
2
0
B
−2
−2,5
Periodische Luftdruckschwankungen werden durch unser
2
Gehör als ein Ton wahrgenommen, wobei die Tonhöhe durch
die Frequenz (= Zahl der Schwingungsperioden je Sekunde,
0
gemessen in Hz(Hertz)) bestimmt wird. Dabei werden jedoch
C
−2
sehr langsame Schalldruckschwankungen als einzelne Ereig2,5
−2,5
0
5
7,5
10
12,5
15
17,5
nisse zeitlich aufgelöst wahrgenommen, während bei mehr
t[ms] →
als ca. 15 − 20 Hz sich ein Tonempfinden ergibt. Dieser
Übergang zwischen der zeitlich aufgelösten Wahrnehmung Abbildung 1. Approximation einer Rechteckschwingung (A) als Summe von
5 Cosinusschwingungen (B), die in (C) dargestellt sind.
und der Empfindung als Ton ist beispielsweise beim Knattern
eines Mopedmotors im Standlauf und einer anschließenden
Ein einzelner Ton besteht also bereits aus vielen Teiltönen
Erhöhung der Drehzahl bei der Abfahrt gut wahrzunehmen.
mit
den Frequenzen if 0 mit i = 1, 2, 3, . . . Sie wird als die
Gemäß der durch Jean Baptist Joseph Fourier (1768–1830)
Obertonreihe
bezeichnet.
entwickelten Fourier–Analyse kann jede periodische Funktion
Trägt
man
die Amplituden–Koeffizienten C i über der Frep(t) mit der Periodendauer T 0 bzw. Frequenz f 0 = 1/T0
quenz
der
Teilschwingungen
auf, so erhält man das sog.
(es gilt also p(t) = p(t + kT0 ) für alle ganzen Zahlen k)
Spektrum
|P
(f
)|
eines
Tons
p(t),
vgl. Bild 2:
in eine Reihe von Cosinus–Schwingungen mit Frequenzen,
die ganzzahlige Vielfache der Grundfrequenz f 0 darstellen,
|P (f )|
entwickelt werden:
p(t) =
∞
Ci cos (2π(if0 )t + φi ) .
f0
i=0
Dabei wird die Teilschwingung C i cos (2π(if0 )t + φi ) als die
i-te Oberschwingung des Tons mit der Amplitude C i und der
Null–Phase φi bezeichnet. (C0 : Gleichanteil)
2f0
1:2
Oktave
Abbildung 2.
intervalle.
2:3
Quinte
3f0
3:4
Quarte
4f0
5f0
f
6f0
4:5
5:6
große Terz kleine Terz
6:7
Linienspektrum eines Tons und die darin enthaltenen Grund-
2
Die Form des Spektrums, also der Gehalt von Oberschwingungen in einem Ton, wird als dessen Klangfarbe wahrgenommen. Hierbei stellen sich zwischen den Teiltönen mit den
Frequenzen f 0 , 2f0 , 3f0 , usw. die Frequenzverhältnisse 1 :
2, 2 : 3, 3 : 4 ein, welche die musikalischen Grundintervalle
Oktave (2 : 1), Quinte (3 : 2), Quarte (4 : 3), große Terz
(5 : 4) usw. bilden. Die Grundelemente der musikalischen Harmonie sind also bereits in einem einzigen Ton enthalten und
sie folgen unmittelbar aus dem mathematischen Prinzip der
Fourier–Analyse, die wie bereits erwähnt, unserem Gehörsinn
entspricht. Diese Reihe der Intervalle Oktave, Quinte, Quarte
usw. tritt auch in der Naturtonreihe von Blechblasinstrumenten
auf (Anregung von unterschiedlichen Schwingungsmoden, d.h.
von unterschiedlich vielen stehenden Wellen im Rohr, durch
Veränderung der Lippenspannung), oder bei Flageolett–Tönen
bei Saiteninstrumenten (Erzeugung von Schwingungsknoten
durch leichtes Auflegen eines Fingers bei ganzzahligen Teilen
der Saitenlänge).
Als dissonant wird die Überlagerung zweier Cosinus–
Schwingungen mit nahe beieinander liegenden Frequenzen
f1 und f2 empfunden, da gemäß der Additionstheoreme der
Trigonometrie gilt:
f2 −f1
2
t
cos
2π
t
.
cos(2πf1 t)+cos(2πf2 t) = 2 cos 2π f1 +f
2
2
Die rechte Seite dieser Gleichung zeigt, dass sich für das
Gehör ein Ton bei einer Tonhöhe einstellt, die der Mittenfrequenz (f 1 + f2 )/2 entspricht. Dieser Ton schwillt mit der
Differenzfrequenz (f 2 − f1 ) an und ab. Ist die Differenzfrequenz (f 2 − f1 ) kleiner als ca. 20 Hz, so findet durch
unser Gehör eine zeitlich aufgelöste Wahrnehmung statt, was
als eine Schwebung empfunden wird. Solche Schwebungen,
allgemeiner gesprochen, eine zugleich zeitliche und spektrale Auflösung eines Akkords, werden musikalisch als dissonant empfunden. Erklingen in einem Akkord mehrere Töne
gleichzeitig, so entsteht durch die Oberschwingungen zu den
einzelnen Tönen ein reichhaltiges Spektrum. Schwebungen
werden dann vermieden, wenn alle diese Oberschwingungen
entweder genügend weit voneinander entfernt auf der Frequenzachse liegen oder genau direkt aufeinander treffen. Rein
gestimmte Intervalle sind durch die Koinzidenz von Oberschwingungen gekennzeichnet. So fallen bei der reinen Oktave
(Frequenzverhältnis 2 : 1) Grund– und Oberschwingungen
des höheren Tons exakt auf jede zweite Oberschwingung des
tieferen Tons. Eine Zuspielung eines um eine oder mehrere
Oktaven höheren Tons verändert also nur die Amplituden
von Oberschwingungen und damit nur die Klangfarbe, nicht
aber die Tonhöhenempfindung. Eine Oktave wird somit nicht
als Akkord wahrgenommen und deshalb werden Töne im
Oktavabstand als harmonisch gleichwertig betrachtet. Dies
wiederum erklärt, weshalb die Tonhöhe als der Logarithmus
der Schwingungsfrequenz wahrgenommen wird: Die Frequenz
ist jeweils zu verdoppeln, um die Tonhöhe um eine Oktave zu
erhöhen. Allgemein gilt:
Tonhöhenempfindung ∼ log 2 (Frequenz/Bezugsfrequenz).
Um zu einer Tonhöhe ein Intervall (z.B. um eine große
Terz) zu addieren, ist also die Schwingungsfrequenz um einen
entsprechenden Faktor (im Beispiel mit 5/4) zu multiplizieren.
Die Logarithmus–Funktion ist nämlich die einzige Funktion
R + → R (R: Menge der reellen Zahlen, R + : Menge der
positiven reellen Zahlen), durch die ein Produkt in eine Summe abgebildet wird. Die logarithmische Tonhöhenempfindung
gehört zum sog. Weber–Fechnerschen Gesetz der logarithmischen Wahrnehmung des Menschen aus der Psychologie, das
in vielen Bereichen gilt (z.B. Lautstärke, Helligkeit, aber auch
z.B. bzgl. materiellen Reichtums: Bei einer Lohnerhöhung
interessiert meist nicht deren Geldwert, sondern nur der Prozentsatz, also der Faktor der Lohnsteigerung).
Bei der reinen Quinte fällt die zweite Oberschwingung
2f2 des höheren Tons mit der Grundfrequenz f 2 genau auf
die dritte Oberschwingung 3f 1 des tieferen Tons mit der
Grundfrequenz f 1 . Es gilt also: 3f1 = 2f2 bzw. f1 : f2 =
2 : 3. So werden bei Streichinstrumenten Quinten dadurch
rein gestimmt, dass darauf geachtet wird, ob eine Schwebung
(d.h. eine langsam periodische Veränderung des Höreindrucks)
durch nicht genau aufeinander fallende Oberschwingungen
wahrzunehmen ist. Bei der Quarte gilt diese Übereinstimmung
zwischen der 4. und der 3. Oberschwingung der Einzeltöne,
bei der großen Terz bei der 5. und 4. Oberschwingung usw..
Zusammenfassend lässt sich feststellen, dass die üblichen musikalischen Intervalle mittelbar aus der Zusammensetzung von
periodischen Funktionen aus Grund– und Oberschwingungen
in der Fourier–Analyse folgen und durch die Vermeidung von
Schwebung durch Koinzidenz von Oberschwingungen gegeben sind. Sie sind somit nicht durch subjektives Empfinden
sondern eindeutig mathematisch begründet. Die Konsonanz
eines musikalischen Intervalls ist durch eine hohe Kommensurabilität der beiden Schwingungsfrequenzen (bzw. der Saiten–
oder Rohrlängen) gegeben, also durch eine Vergleichbarkeit
mit Hilfe eines möglichst großen gemeinsamen Massstabes. Im
Altertum wurde diese Eigenschaft der musikalischen Harmonie ausschließlich philosophisch ästhetisch begründet. Obertonreihe und Fourier–Analyse bestätigen diesen ästhetischen
Anspruch mathematisch.
III. M USIKALISCHE S TIMMUNGSSYSTEME
A. Das System des Philolaos (ca. 450 v. Chr.)
Die Einteilung einer Oktave in Teiltöne, die Tonleiter,
erfolgte mathematisch begründet wohl erstmalig in der Philosophenschule der Pythagoräer. Als erstes ist das System des
Philolaos (ca. 450 v. Chr.) überliefert. Damals wurden nicht
Frequenzverhältnisse sondern Verhältnisse von Saitenlängen
betrachtet. Da aber bei gleichen Saitenspannungen (, was z.B.
durch gleiche Zuggewichte sichergestellt werden kann,) die
Schwingungsfrequenz einer Saite umgekehrt proportional zur
Saitenlänge ist, ergibt sich ein Quotient f 2 /f1 zweier Schwingungsfrequenzen als Kehrwert des Quotienten der zugehörigen
Saitenlängen l 2 : l1 , d.h. es gilt f2 : f1 = l1 : l2 . Beide
Masssysteme sind damit völlig gleichwertig. Aufgrund der
größeren Anschaulichkeit und dem näheren Bezug zu Physik
werden hier Intervalle ausschließlich durch Frequenzverhältnisse ausgedrückt. Für Saitenlängen–Verhältnisse (oder auch
Rohrlängen–Verhältnisse bei Blasinstrumenten) gelten deren
Kehrwerte.
3
Philolaos unterteilt die als natürliches Ur–Intervall erkannte
Oktave (f2 = 2f1 ) zunächst gemäß dem arithmetischen Mittel
der Frequenzen
1
3
(f1 + 2f1 ) = f1 = f2 ⇒ f2 : f1 = 3 : 2 Quinte
2
2
und erhält dadurch die Quinte. Ebenso wird das harmonische
Mittel, das als der Kehrwert des arithmetischen Mittels der
Kehrwerte definiert ist, aus dem Oktavintervall gebildet:
1
4
= f1 = f2 ⇒ f2 : f1 = 4 : 3 Quarte.
1
1
1
3
+
2
f1
2f1
Es entsteht damit die Quarte zum Grundton. (Dem harmonischen Mittel zweier Schwingungsfrequenzen entspricht das
arithmetische Mittel der zugehörigen Saitenlängen und umgekehrt.) Der Abstand (d.h. der Quotient der Frequenzen)
zwischen Quinte und Quarte wird als Ganzton definiert:
3
4
9
f0 : f0 =
⇒ f2 : f1 = 9 : 8
Ganzton.
2
3
8
Damit teilt sich die Quarte in 2 Ganztöne und einen sog.
Halbton x mit,
256
9 9
def 4
· ·x = ⇒x=
⇒ f2 : f1 = 256 : 243 Halbton
8 8
3
243
die Quinte in 3 Ganztöne und diesen Halbton. Die Dur–
Tonleiter ist so durch die Definition von Quinte, Quarte,
Ganzton, Halbton eindeutig fixiert. Im System des Philolaos
ergeben sich z.B. für C–Dur die in Bild 3 dargestellten
Frequenzen (bezogen auf die Frequenz f 0 des Grundtons C
(= 264 Hz)).
C
D
E
F
G
A
H
c
1
9
8
81
64
4
3
3
2
27
16
243
128
2
9
8
Abbildung 3.
9
8
256
243
9
8
9
8
9
8
256
243
Frequenzskala der Dur–Tonleiter nach Philolaos.
Da für alle Quinten und Quarten die Frequenzverhältnisse
3 : 2 bzw. 4 : 3 vorliegen, sind somit alle Quinten und Quarten
rein im Sinne koinzidierender Obertöne. Hingegen entstehen
die große Terzen als zwei Ganztöne mit (9/8) 2 = 81/64 um
den Faktor 81/80 zu groß und klingen damit ziemlich unrein
(5 : 4 = 80 : 64 < 81/64). Dieser Fehler 81/80 = 1,0125
wird als das syntonische Komma in Stimmungssystemen bezeichnet. Des Weiteren ist der Halbton weit weniger als ein
halber Ganzton, da gilt: (256/243) 2 = 1,1099 < 1,125 = 9/8.
Insgesamt führt das System des Philolaos aufgrund dieser
Schwächen zu einem ziemlich unbefriedigenden Höreindruck.
B. Chromatische Erweiterung, Pythagoreisches Komma
Im System des Philolaos (bzgl. Grundton C) sind alle
einzelnen Quinten in der Folge F–C–G–D–A–E–H rein. Diese
Töne (bzw. ihre Schwingungsfrequenzen bzgl. eines Bezugstons (hier F)) sind also durch das Aufeinandertürmen von
Quinten (und als selbstverständlich vorausgesetzten Oktavverschiebungen) vorgegeben. Dieses Prinzip kann zur Erzeugung
weiterer Töne fortgesetzt werden, wodurch sich nährungsweise
die chromatische Halbtonreihe ergibt, denn man trifft nach 12
Quinten knapp neben den Grundton (plus 7 Oktaven):
(3/2)12 = 129,746... = 27 = 128.
Diese Nähe von 12 Quinten zu 7 Oktaven hat dazu geführt,
dass die Oktave bei großzügigem Hinwegsehen über den
Fehler in 12 Habtonschritte unterteilt wird, also zur gewohnten
chromatischen Tonreihe. Es entsteht jedoch durch fortlaufende
reine Quinten kein Quintenzirkel, sondern eine sich niemals
schließende Quintenspirale, siehe Bild 4.
his 312/219
311/217 eis
C1
F 2/3
310/215
59049
32768
19687
16284
g 3/2
ais
d 9/8
B 16/9
Es 32/27
dis
W olfsquinte
a 27/16
As 128/81
D es
gis
6561
4096
e 81/64
G es 1024/729
h 243/128
cis
2187
2048
Abbildung 4.
fis 729/512
Spirale reiner Quinten (reduziert um Oktaven).
Die Abweichung zwischen 12 Quinten und 7 Oktaven, also
12
12
= 3219 = 1,013643, wird als das Pythagoder Faktor (3/2)
27
reische Komma bezeichnet. Schließt man die Quintenspirale
an einer Stelle, z.B. zwischen es und gis zwangsweise, so
wird diese Quinte“ von 1,5 auf 1,4798 verkleinert und damit
”
extrem unrein. Dies wird als Wolfsquinte“ bezeichnet.
”
Auch bei vielfachen Umläufen dieser Quintenspirale, also
der Definition weiterer Töne zwischen den 12 Tönen der
Klaviatur innerhalb einer Oktave, kann der Ausgangston (bzw.
Oktavverschiebungen dazu) niemals wieder erreicht werden,
denn in der Quinte steckt der Primfaktor 3, während Oktaven
als Potenzen von 2 definiert sind:
(3/2)k = 2 bzw. 3k = 2+k ∀k, ∈ N.
Ein widerspruchsfreies musikalisches Stimmungssystem, das
über reinen Quinten definiert ist, kann aufgrund der Eindeutigkeit der Zerlegung von natürlichen Zahlen in Primfaktoren
somit prinzipiell nicht existieren! Auch mit der Definition unterschiedlicher Tonhöhen je nach enharmonischer Darstellung,
also z.B. eine Unterscheidung zwischen es und dis etc., wird
dieses Problem nicht endgültig gelöst. Sogenannte subsemitonische Tasteninstrumente mit mehrfacher Repräsentation der
einzelnen Töne innerhalb der chromatischen Skala, mit denen
in der Renaissance– und Frühbarockzeit experimentiert wurde
(z.B. das sog. Cembalo universale“ mit 32 Tasten je Oktave)
”
konnten letztlich keine befriedigende Abhilfe schaffen. Durch
professionelle Musiker erfolgt bei nicht fixierter Intonation,
4
also z.B. bei Streichern oder im Chorgesang, eine rein klingende Intonation fortlaufend fließend, also mit einer Variabilität
der Höhe für identisch notierte Töne zum Ausgleich von
syntonischem und Phytagoreischem Komma.
A
C
9:8
6:5
groß
1
Abbildung 6.
C. Das Stimmungssystem des Archytas
H
d
klein
e
f
3:2
8:5
groß
4:3
g
groß
a
klein
9:5
2
Frequenzskala einer äolischen Moll–Tonleiter nach Archytas.
Archytas (ca. 420–350 v. Chr.) definierte eine sog. reine
Stimmung innerhalb einer Tonart, die auch als diatonische
Stimmung bezeichnet wird. (Sie wird auch Didymus zugeschrieben; Didymus lebte jedoch erst ca. 300 Jahre später.)
Wiederentdeckt und ausführlich diskutiert wurde dieses System durch Gioseffo Zarlino (1517–1590, Markuskantor zu
Venedig), dem wohl wichtigsten Kenner und Entwickler von
Stimmungssystemen der Musikgeschichte.
Im System des Archytas werden Quinte und Quarte wie
bei Philolaos über geometrisches und harmonisches Mittel aus
der Oktave bestimmt. Davon abweichend werden jedoch große
und kleine Terz als arithmetische und harmonische Mittel aus
der Quinte definiert. Damit entsprechen diese Terzen exakt der
Obertonreihe, das syntonische Komma wird vermieden.
einer chromatischen Erweiterung. Diese wurde im Jahr 1739
durch Leonhard Euler (1702–1783), einem der bedeutendsten Mathematiker, anhand der Erkenntnis versucht, dass in
der natürlichen Obertonreihe der 7., 11., 13. Oberton und
alle weiteren Primzahlen entsprechenden Obertöne nach unserem musikalisch harmonischen Empfinden als sehr fremd
klingen. Diese entsprechen nämlich nicht dem harmonischen
Grundkonzept der Kadenz, das über die reinen Dreiklänge
wiederum unmittelbar aus der diatonischen Stimmung folgt.
Deshalb legte Euler fest, dass alle Töne einer chromatischen
Tonleiter durch Frequenzen definiert seien, die bzgl. einer
Bezugsfrequenz ausschließlich mittels der Primfaktoren 2, 3
und 5 darstellbar sind, also durch 2 α · 3β · 5γ mit α, β, γ ∈ N
definiert werden. Damit ergeben sich auch für alle Intervalle
Frequenzverhältnisse, bei denen Zähler und Nenner mittels
3
5
f1 + f1 /2 = f1 = f2 ⇒ f2 : f1 = 5 : 4 große Terz dieser ersten drei Primzahlen ausdrückbar sind. Das System
2
4
von Euler ist aus mathematischer Sicht gewiss ästhetisch;
1
6
= f1 = f2 ⇒ f2 : f1 = 6 : 5 kleine Terz. es erweist sich aber für die musikalische Praxis als völlig
1
1
2
5
ungeeignet, da extrem unterschiedlich große Halbtonschritte
2 f1 + 3f1
Es entsteht auf diese Weise die diatonische oder auch rein“ auftreten.
”
genannte Skala, für die sich am Beispiel von C–Dur ergibt,
siehe Bild 5
D. Die mitteltönige Stimmung
c
d
groß
1
Abbildung 5.
e
f
5:4
4:3
klein
9:8
g
groß
a
klein
3:2
h
c
15:8
2
groß
5:3
Frequenzskala der Dur–Tonleiter nach Archytas.
Die Skala zeichnet sich dadurch aus, dass die Dur–
Dreiklänge auf den Stufen 1, 4 und 5 (also die Kadenz) rein
erklingen (Frequenzverhältnisse 1, 5/4, 3/2), sowie auch
die Moll–Dreiklänge der Stufen 3 und 6 (1, 6/5, 3/2). Als
gravierende Nachteile sind jedoch anzumerken: Es existieren
zweierlei Ganzton–Intervalle 9 : 8 und 10 : 9, was jedoch
genau der Obertonreihe entspricht. Die Differenz dieser beider
Ganztonschritte (Quotient der Frequenzen) entspricht dem
syntonischen Komma 81/80; die Terz
2 dadurch korrigiert.
wird
= 1,1378 mehr als
Außerdem ergeben zwei Halbtöne 16
15
den großen“ Ganzton 98 = 1,125. Die kleine Terz auf der 2.
”
Stufe (d–f) ist mit 32
27 = 1,185 anstelle von 1,2 unrein. Auch
die Quinte auf der 2. Stufe (d–a) ist mit 40
27 = 1,4815 um das
syntonische Komma verkleinert. Der Moll–Dreiklang auf der
2. Stufe (Subdominante in a–Moll) ist damit auch bei der sog.
reinen“ Stimmung grob unrein!
”
Durch Verschiebung von großen“ und kleinen“ Ganztönen
”
”
lässt sich auch eine diatonische, reine“ Stimmung für die
”
äolische Moll–Skala erzeugen; siehe Bild 6.
Dabei entsteht jedoch nun ein grob unreiner Dur–Dreiklang
auf der 7. Stufe (g–Dur bzgl. des Grundtons A)! Der gravierendste Nachteil im System des Archytas ist das Fehlen
In der mitteltönigen Stimmung, die wohl erstmalig von
Zarlino im Jahr 1539 vorgeschlagen wurde, wird das Problem
der um das syntonische Komma zu großen Terzen im System
des Philolaos auf Kosten zu kleiner Quinten gelöst. Da vier
Quinten eine große Terz (+ zwei Oktaven) ergeben, siehe Bild
4, wird
in der mitteltönigen
Stimmung die Quinte um den
Faktor 4 80/81 zu qm = 4 80/81 · 3 : 2 = 1,495348 < 1,5
verkleinert.
Der Fehler für die Quinte ist also auf nur ein Viertel des syntonischen Kommas verringert, weshalb bei der mitteltönigen
Stimmung die Dreiklänge der Kadenz als wesentlich angenehmer empfunden werden als im System des Philolaos. Jedoch
ergeben 12 mitteltönige Quinten weniger als 7 Oktaven, da
gilt:
12 3
1/4
12 80
3
80
3
·
=
·
= 125 < 128 = 27 .
2
81
2
81
Hier entsteht also eine Quintenspirale nach innen mit einer
noch gravierenderen Wolfsquinte als im System des Philolaos.
Aber solange Wolfsquinten vermieden werden erzeugt die
mitteltönige Stimmung ein heute seltsam weich anmutendes
Klangbild, das sich insbesondere in der Alten Musik effektvoll einsetzen lässt. Die mitteltönige Stimmung wurde in
Deutschland insbesondere durch Michael Praetorius (1571–
1621) propagiert und fand zeitweise große Verbreitung. (In
England gibt es angeblich heute noch Kirchenorgeln, die
gemäß der mitteltönigen Stimmung intoniert sind.)
5
E. Die gleichschwebende Stimmung
Um den Quintenzirkel bei 7 Oktaven exakt zu schließen,
liegt es nahe, eine Definition der Quinte gemäß
√ 7
12
2 = 1,4983071 < 3/2
q 12 = 27 ⇒ q =
vorzunehmen. Dies entspricht zugleich einer
√ Einteilung der
Oktave in 12 gleiche Halbtöne zu je p = 12 2 = 1,05946.
Die Fehler von syntonischem und Pythagoreischem Komma werden gleichmäßig auf alle Intervalle verteilt. Diese
als gleichschwebend bezeichnete Stimmung wurde erstmalig
ebenfalls durch Gioseffo Zarlino in seinen Sopplimenti musi”
cali“ von 1588 vorgeschlagen. In diesem Stimmungssystem ist
jedoch kein einziges Intervall außer der Oktave wirklich rein!
Die Frequenzverhältnisse sind sogar alle irrational und damit
grundsätzlich inkommensurabel. Die ästhetischen Ansprüche
der alten Philosophen werden damit in krassester Weise verfehlt.
Aus mathematischer Sicht ist jedoch die gleichschwebende
Stimmung als interessant zu bezeichnen, da bei Definition
einer Identität von Tönen bzgl. Oktavverschiebungen die 12
Halbtöne der Oktave die höchst ästhetische Struktur einer
mathematischen Gruppe G mit 12 Elementen bilden, wobei
als die Verknüpfung zwischen Elementen die Intervallbildung
I dient:
I = pa ◦ pb
def
=
p(a−b)mod12 ∈ G;
a,b ∈ {0, 1, . . . , 11} , p =
√
2.
12
In mathematischen Gruppen herrscht eine hohe Symmetrie.
Ausgehend von einem Element sind die Beziehungen zu
allen anderen Elementen unabhängig vom Ausgangselement
jeweils gleich. Intervalle sind hier somit in allen Tonarten
völlig identisch. Die verschiedenen Tonarten verlieren dadurch
jedoch gänzlich ihre musikalischen Eigenarten und speziellen
Ausdrucksmöglichkeiten. Die gleichschwebende Stimmung,
die heute allen elektronischen Stimmgeräten zugrunde liegt
und bei Tasteninstrumenten verwendet wird, ist nicht zu verwechseln mit einer sog. wohltemperierten“ Stimmung. Sie
”
ist im Gegenteil eher als kalt und unpersönlich zu charakterisieren. In der musikalischen Praxis wird auch von der
gleichschwebenden Stimmung intuitiv abgewichen, sobald die
Möglichkeit für eine individuelle Feinintonation besteht, wie
bei Sängern, Streichern und Bläsern. Bei guten Interpreten
entsteht eine variable Stimmung, die sich jeweils an der
aktuellen diatonischen Reihe mit möglichst reinen Quinten,
Quarten und Terzen orientiert.
F. Weitere Stimmsysteme
Die Definition eines widerspruchsfreien musikalischen
Stimmungssystems ist aus folgendem Grund prinzipiell
unmöglich: Aus dem logarithmischen Zusammenhang zwischen Schwingungsfrequenz und Tonhöhenempfindung entsprechen Tonhöhenschritten Multiplikationen von Frequenzverhältnissen, während in der Obertonreihe der Fourier–
Analyse jeweils die Grundfrequenz zu addieren ist, um den
nächsten Oberton zu erreichen. Im Laufe der Musikgeschichte
wurden neben den bereits erwähnten unüberschaubar viele
weitere Kompromisse vorgeschlagen, um dieses grundsätzliche Problem so gut wie möglich vor Musikern und Musikgenießern zu verbergen.
Neben zahlreichen großen Mathematikern und Physikern
wie Euler, Kepler oder Huygens haben sich auch viele
berühmte Instrumentenmacher intensiv mit diesem Problem
beschäftigt. So sind mindestens 5 Vorschläge aus der Orgelbauerfamilie Silbermann und zahlreiche weitere Vorschläge
von Vorgängern, Zeitgenossen und Schülern von Johann Seb.
Bach bekannt. Zum Beispiel hat allein der Musiker und
Musiktheoretiker Andreas Werckmeister (1645–1706) mindestens 7 unterschiedliche Stimmungssysteme entwickelt. In der
Barockzeit war also das grundsätzliche Stimmungsproblem
allgemein bekannt und ein unter Musikern viel diskutiertes
Thema. Leider ist nicht überliefert, welchem dieser vielen
Stimmungssysteme Johann Seb. Bach den Vorzug gegeben hat,
die Zeugnisse seiner Schüler widersprechen sich hierzu. Die
Komposition der beiden Bände des wohltemperirten Claviers“
”
von J.S. Bach hat aber sicherlich nicht dazu gedient, ein
neues, umfassendes und rund um den Quintenzirkel gleichermaßen einsetzbares Stimmungssystem zu propagieren, sondern
es ist eher als ein Kompendium von Referenzstücken zu
verstehen, anhand dessen unterschiedliche Stimmungssysteme
verglichen werden können. Nach Ansicht des Autors ist das
wohltemperirte Clavier“ damit also als eine Art Benchmark–
”
”
Test“ zum Vergleich von verschiedenen Stimmungssystemen
(, wie man Benchmark–Software für den Leistungsvergleich
bei Computern einsetzt). Da die gleichschwebende Stimmung
bereits lange vor Werckmeister und Bach etc. bekannt war,
darf man wohl mit hoher Gewissheit annehmen, dass diese
für die Barockmeister und auch für spätere Musiker keine
akzeptable Lösung darstellte. Man strebte eine wärmere, d.h.
temperierte“ Stimmung mit Beibehaltung von Eigenarten
”
der verschiedenen Tonarten an. Richard Wagner hat wohl
hinsichtlich des Einsatzes von Tonarten mit unterschiedlichen
charakteristischen Färbungen als höchst effektvolles Stilmittel
später die höchste Meisterschaft erreicht.
Üblicherweise werden heute Stimmungssysteme anhand ihrer Abweichung von der gleichschwebenden Stimmung charakterisiert, wobei als logarithmisches Maß für die Tonhöhe
der hundertste Teil, ein Cent, eines Halbtonschrittes der gleichschwebenden Stimmung verwendet wird:
Tonhöhe = 1200 · log 2 f /fBezug [Cent] .
Der Oktave entsprechen somit 1200 Cent, der Quarte 700
Cent. In Bild 7 wird die Abweichung mehrerer Stimmungssysteme von der gleichschwebenden Stimmung in Cent für
alle Töne der chromatischen Reihe dargestellt, wobei auch
eine Rekonstruktion“ der von Bach bevorzugten Stimmung
”
gemäß Angaben von Schülern enthalten ist. Diese darf jedoch
keineswegs als gesichert betrachtet werden.
IV. Z USAMMENFASSUNG
In diesem Beitrag wurde versucht zu zeigen, dass
musikalisch–ästhetisches Empfinden und mathematische Analyse in sehr enger Beziehung stehen, was übrigens auch für
6
+ 30
15, 6
13, 7
0
Philolaos
11, 7
9, 78
7, 82
5, 87
3, 91
1, 96
0
0
-1, 96
-3, 91
-5, 87
- 30
10,3
6,8
mitteltönig
3,4
0
0
-3,4
-6,8
-10,3
-13,7
-17,1
-20,5
-24
Werckmeister III
Silbermann II
-27,4
0
0
-2
-10
-8
Archytas
-4
-8
-10
-8
-12
-12
6
4
2
0
0
-2
-4
-6
-8
0
-10
-12
-14
Ä%DFK³
-4
-6
-16
0
0
0
0
-2
-4
-8
-5
-6
-10
-10
3, 9
-10
2
0
1
Euler
0
-2
-13
-14
3, 9
2
1
0
0
-2
- 10
- 13
- 14
- 13
- 17
- 25
- 29
c
Abbildung 7.
cis
d
es
e
f
fis
g
gis
a
b
h
Fµ
Stimmungssysteme im Vergleich zur gleichschwebenden Stimmung.
andere Kunstformen in gleicher Weise gilt. Eine Beschäftigung mit der Mathematik, die hinter unseren musikalischen
Hörgewohnheiten steckt, lohnt sich nicht nur aus generellem
Interesse, sondern kann nach Erfahrung des Verfassers auch
zu einem gesteigerten Musikgenuss verhelfen.
Die musikalischen Intervalle entsprechen rationalen Frequenzverhältnissen mit möglichst kleinen ganzen Zahlen in
Zähler und Nenner. Sie sind in der Obertonreihe, also der
Folge von Schwingungsfrequenzen, die sich aus der Fourier–
Analyse periodischer Zeitverläufe bzw. direkt als Naturtonreihe von (Blech–)Blasinstrumenten ergibt, auf natürliche Weise
enthalten. Die Eindeutigkeit der Zerlegung von natürlichen
Zahlen in Primfaktoren lässt aber prinzipiell nicht zu, dass
mehrere aufeinander gestellte gleiche Intervalle, die selbst
keine Oktaven darstellen, sich zu Oktaven addieren. Somit
können widerspruchsfreie musikalische Stimmungssysteme,
bei denen mehr als eine Tonhöhe je Oktave zugelassen
sind, prinzipiell nicht existieren. Die übliche Unterteilung der
Oktave in 12 Halbtöne erfolgt daraus, dass sich 12 reine
Quinten relativ nahe zu 7 Oktaven ergeben und dadurch im
sog. Quintenzirkel, der jedoch eigentlich eine Spirale darstellt,
zumindest in sehr grober Näherung ein abgeschlossenes Sys”
tem“ entsteht.
Im Laufe der Musikgeschichte wurde auf vielfältige Weise
versucht, zu Kompromissen zu gelangen, die jeweils mit
deutlich unterschiedlichen klanglichen Eigenheiten verbunden
sind. Die heute meist als selbstverständlich vorausgesetzte
gleichschwebende Stimmung trifft dabei jedoch nicht die
Klangvorstellungen von Musikern früherer Epochen. Sie stellt
nach Meinung des Verfassers eine Verarmung bzgl. des musikalischen Empfindens dar, da die unterschiedlichen Charakte-
ristika verschiedener Tonarten verloren sind. Im Rahmen der
heute populären Historischen Auff ührungspraxis sind daher
nicht nur Tempi und Klangfarben von Instrumenten an alten
Idealen auszurichten, sondern es ist auch insbesondere das
ursprünglich verwendete Stimmungssystem einzusetzen, um
dem Originalklang möglichst nahe zu kommen.
L ITERATUR
[1] G. Assayag, H.G. Feichtinger, J.F. Rodrigues: Mathematics and Music
– A Diderot Mathematical Forum; Springer–Verlag Berlin Heidelberg
2002
[2] Knut Radbruch: Mathematik in den Geisteswissenschaften, Vandenhoeck
u. Ruprecht, Göttingen, 1989, (Kleine Vandenhoeck–Reihe: 1540)
[3] Ambros P. Speiser: Musikalische Akustik; VCH Verlagsgesellschaft
mbH, Weinheim; Physik in unserer Zeit, 20. Jahrgang 1989, Nr. 5, S.
138–143
Johannes B. Huber ist Professor für Nachrichtentechnik an der Friedrich–Alexander–Universität
Erlangen–Nürnberg und leitet dort den Lehrstuhl für
Informationsübertagung (www.LNT.de/LIT). Musikalisch ist er als Amateur aktiv.