Die Maxwell`schen Gleichungen

Die Maxwell’schen Gleichungen
1
Einführung
Inhalt
D
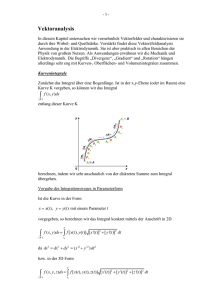
1.1 Gradient, Rotation
und Divergenz . . . . . . . . . . . . . . . .
1
1.2 Die Integralsätze
im Fall des Ê 3 . . . . . . . . . . . . . . . .
7
ie empirische Basis der Elektrodynamik ist durch das Induktionsgesetz, das Gauß’sche Gesetz, das Biot-Savart’sche Gesetz
sowie durch die Lorentz-Kraft und die universelle Erhaltung der
elektrischen Ladung gegeben. Dies sind die Gesetzmäßigkeiten, die
sich in realistischen Experimenten bestätigen oder, schlimmstensfalls, widerlegen lassen. Die integrale Form der Grundgesetze enthält
ein-, zwei- oder dreidimensionale Objekte, d. h. lineare Leiter, Leiterschleifen, räumliche Ladungsverteilungen oder Ähnliches, und hängt
daher immer von konkreten experimentellen Anordnungen ab. Um
den Zusammenhängen zwischen scheinbar ganz unterschiedlichen
Phänomenen auf den Grund zu gehen, muss man aus der integralen
Form der empirisch getesteten Gesetze auf lokale Gleichungen übergehen, die mit den integralen Aussagen verträglich sind. Erst dann
entstehen die grundlegenden partiellen Differentialgleichungen, die
wir die Maxwell’schen Gleichungen nennen und die bis heute alle
elektromagnetischen Erscheinungen richtig beschreiben.
Dieser Übergang von integralen zu lokalen Gesetzen bezieht seine
mathematischen Hilfsmittel zunächst ,,nur“ aus der Vektoranalysis
auf dem Euklidischen R3 und dem bekannten Differentialkalkül auf
diesem. Allerdings, da die elektromagnetischen Felder i. Allg. auch
von der Zeit abhängen und somit über der Raumzeit R4 definiert
sind, reicht diese nicht aus und muss auf mehr als drei Dimensionen verallgemeinert werden. Diese Verallgemeinerung wird besonders transparent und damit letztlich besonders einfach, wenn man den
sog. äußeren Kalkül verwendet.
Die Phänomenologie der Maxwell’schen Gleichungen entwickeln
wir in diesem Kapitel zunächst anhand der vollen, zeit- und ortsabhängigen Gleichungen, und reduzieren diese erst in einem zweiten
Schritt auf stationäre bzw. statische Verhältnisse.
1.1 Gradient, Rotation und Divergenz
Die Elektrodynamik und ein Großteil der klassischen Feldtheorie leben
auf flachen Räumen Rn der Dimension n. Dabei bildet bei statischen
oder stationären Prozessen der gewöhnliche dreidimensionale Raum
R3 , in allen anderen Fällen die vierdimensionale Raumzeit mit n = 4
F. Scheck, Theoretische Physik 3
c Springer 2010
DOI 10.1007/978-3-642-03962-1, 1.3 Maxwell’sche Gleichungen
in integraler Form . . . . . . . . . . . . . 10
1.4 Die Maxwell’schen
Gleichungen in lokaler Form . . 20
1.5 Skalare Potentiale
und Vektorpotentiale . . . . . . . . . . 33
1.6 Phänomenologie der
Maxwell’schen Gleichungen . . . 44
1.7 Statische elektrische
Zustände . . . . . . . . . . . . . . . . . . . . . . 53
1.8 Stationäre Ströme
und statische magnetische
Zustände . . . . . . . . . . . . . . . . . . . . . . 78
1
2
1
Die Maxwell’schen Gleichungen
den adäquaten mathematischen Rahmen. Solche Räume sind besonders einfache Spezialfälle von glatten Mannigfaltigkeiten, auf denen
man verschiedene geometrische Objekte und einen Differentialkalkül
vorfindet, mit dessen Hilfe man Beziehungen zwischen diesen, d. h.
letztlich physikalische Bewegungsgleichungen aufstellen kann. Ist z. B.
Φ(x) = Φ(x 1 , x 2 , . . . , x n ) eine glatte Funktion auf Rn , so ist das daraus
gebildete Gradientenfeld wie folgt
∂Φ(x) ∂Φ(x)
∂Φ(x) T
grad Φ(x) =
,
,
.
.
.
(1.1)
∂x n
∂x 1
∂x 2
definiert. Im R3 ist grad der bekannte Differentialoperator (,,Nablaoperator“)
∂
∂
∂ T
∇=
,
,
.
∂x 1 ∂x 2 ∂x 3
Beispiel 1.1
Es werde eine (kleine) Probemasse m in das Gravitationsfeld zweier
gleicher, punktförmiger Massen M gesetzt, die sich an den Orten x(i) ,
i = a, b, befinden. Das Potential am Ort x der Probemasse ist dann
1
1
Φ(x) ≡ U(x) = −G N m M
+
.
|x − x(a) | |x − x(b) |
Ohne Beschränkung der Allgemeinheit kann man das Bezugssystem so
legen, dass x(b) = −x(a) ist. Das aus diesem Potential abgeleitete Kraftfeld ist dann
x − x(a)
x − x(b)
F(x) = −∇x Φ(x) = −G N m M
+
|x − x(a) |3 |x − x(b) |3
x − x(a)
x + x(a)
.
= −G N m M
+
|x − x(a) |3 |x + x(a) |3
Dies ist ein konservatives Kraftfeld, das man sich leicht am Beispiel
x(a) = (d, 0, 0)T , x(b) = (−d, 0, 0)T zeichnerisch veranschaulicht.
n
Ist êi , i = 1, . . . , n, eine Basis, V = i=1
V i (x)êi ein Vektorfeld, so
ist die Divergenz dieses Vektorfeldes als
n
∂ i
V (x)
div V =
∂x i
(1.2)
i=1
definiert. Auch dies ist eine im R3 wohlbekannte Konstruktion. Insbesondere wenn V ein Gradientenfeld ist, V = ∇Φ(x), dann ist seine
Divergenz gleich
div grad Φ =
3
∂ 2 Φ(x)
i=1
∂(x i )2
= Φ(x) .
1
1.1 Gradient, Rotation und Divergenz
Die Aussage, dass die Rotation eines Vektorfeldes wieder ein Vektorfeld
ist, ist allerdings eine Besonderheit der Dimension 3. Im R3 hat
rot V = ∇ × V
(1.3a)
in der Tat drei Komponenten. In kartesischen Komponenten ausgedrückt
sind diese
∂V 3 ∂V 2
∇×V 1 = 2 − 3
(und zyklisch ergänzt) ,
(1.3b)
∂x
∂x
oder mithilfe des ε-Tensors in drei Dimensionen formuliert,
3
3
i 1 ∂Vk
∂Vk ∂V j
εijk
−
=
εijk j .
(1.3c)
∇×V =
2
∂x j ∂x k
∂x
j,k=1
j,k=1
Den tieferen Grund für diese Verwandtschaft haben wir in Band 1,
Kap. 5, ausgearbeitet, wir kommen hierauf aber auch in diesem Band
ausführlich zurück (s. Abschn. 2.1.2). Bemerkenswert ist allerdings
auch, dass ∇ × V kein ganz ,,richtiges“ Vektorfeld sein kann, denn
das Transformationsverhalten von V und das seiner Rotation unter
Raumspiegelung sind entgegengesetzt: wenn V sein Vorzeichen unter P
ändert, dann bleibt ∇ × V invariant.
Bemerkungen
1. Über dem R3 , der die einfache Metrik gik = δik zulässt, besteht kein
Unterschied zwischen den kontravarianten Komponenten V i von V
und den kovarianten Komponenten Vi . Deshalb kann man statt wie
in (1.3b) – und wie in (1.3c) vorweg genommen – auch
1 ∂V3 ∂V2
∇×V = 2 − 3
(und zyklisch ergänzt) .
∂x
∂x
schreiben. Wie die nun folgende Bemerkung erläutert, ist diese leicht
modifizierte die eigentlich richtige Definition der Rotation.
2. Auf dem Rn oder, allgemeiner, auf der glatten Mannigfaltigkeit M n
der Dimension n – falls diese einen metrischen Tensor g = {gik }
besitzt – , kann man anstelle der kontravarianten Komponenten
Vi
des Vektorfeldes V die kovarianten Komponenten Vi = k gik V k
einführen. Damit lässt sich als Verallgemeinerung der Rotation ein
schiefsymmetrisches Tensorfeld zweiter Stufe
rot V ≡ C ,
mit Cik =
∂
∂
Vk − k Vi
i
∂x
∂x
definieren. Da Cki = −Cik gilt, hat dieser Tensor 12 n(n − 1) Komponenten, in der Dimension n = 2 also eine, in Dimension n = 3 drei,
in Dimension n = 4 sechs Komponenten usw. Man sieht somit schon
hier, dass die Rotation nur über dem R3 die richtige Anzahl Komponenten hat, um wie ein Vektorfeld behandelt werden zu können.
3
4
1
Die Maxwell’schen Gleichungen
3. Aus der vorhergehenden Bemerkung folgt, dass es nur in Dimension
n = 3 sinnvoll ist, die Divergenz einer Rotation zu bilden. Dann gilt
die Aussage
ijk ∂ ∂
ε
Ak = 0 .
(1.4)
div rot A ≡ ∇ · ∇ × A =
∂x i ∂x j
i, j,k
Dies ist gleich Null, weil der ε-Tensor, der in i und j antisymmetrisch ist, mit dem symmetrischen Produkt der beiden Ableitungen
multipliziert wird. Ganz allgemein ist die Kontraktion eines in zwei
Indizes symmetrischen Tensors mit einem in denselben Indizes antisymmetrischen Tensor gleich Null. Dies bestätigt man leicht durch
direktes Nachrechnen.
4. Die bekannte Aussage, dass
eines glatten Gradienten
die Rotation
feldes gleich Null ist, ∇ × ∇Φ(x) = 0, die man aus dem R3 kennt,
gilt allgemein:
rot grad Φ(x) = 0 .
(1.5)
Dies folgt aus der Gleichheit der gemischten Ableitungen von Φ(x).
5. Auch in Dimension n = 3 gibt die Kombination aus Divergenz und
Gradient den Laplace-Operator, im Rn zum Beispiel
div grad Φ =
n
∂ 2 Φ(x)
∂(x i )2
i=1
= Φ(x) .
Auf einer Mannigfaltigkeit M n , die nicht flach ist, oder schon auf
Rn bei Verwendung von krummlinigen Koordinaten gilt eine etwas
allgemeinere Formel, die den metrischen Tensor und Ableitungen
davon enthält und auf die wir weiter unten zurück kommen.
Beispiel 1.2
Potential einer kugelsymmetrischen Ladungsverteilung: Es sei (r) eine
ganz im Endlichen liegende, stückweise stetige Ladungsverteilung, die
im Integral die Gesamtladung Q enthält. Dies bedeutet, dass man eine
Sphäre S2R mit Radius R um den Ursprung (dem Symmetriezentrum der
Ladungsverteilung) legen kann, außerhalb derer (r) verschwindet. Die
Normierungsbedingung besagt, mit d3 x = r 2 dr d(cos θ) dφ,
∞
R
2
d x (r) = 4π r dr (r) = 4π r 2 dr (r) = Q .
3
0
0
Aus der Ladungsdichte (r) werde die differenzierbare Funktion
⎧ r
⎫
∞
⎨1 ⎬
U(r) = 4π
r 2 dr (r ) + r dr (r )
⎩r
⎭
0
r
1
1.1 Gradient, Rotation und Divergenz
gebildet. Für r R ergibt sie zusammen mit der Normierungsbedingung
die einfache Form U(r) = Q/r, das ist nichts Anderes als das CoulombPotential zur Ladung Q. Für kleinere Werte der Radialvariablen weicht
U(r) i. Allg. von dieser einfachen Form ab. Ist z. B. eine homogene Ladungsverteilung vorgegeben,
3Q
(r) =
Θ(R − r) , mit
4πR3
Θ(x) = 1 für x 0 , Θ(x) = 0 für x < 0
der Heaviside-Funktion, so ist
Q 3 2 1 2
für r R ,
R − r
Uinnen (r) = 3
2
2
R
Q
Uaußen (r) =
für r > R .
r
Im Innenbereich ist das Potential U(r) parabelförmig, im Außenbereich
fällt es mit 1/r ab. An der Stelle r = R sind U(r) und seine erste Ableitung stetig, für die zweite Ableitung gilt dies aber nicht. Berechnet
man das (negative) Gradientenfeld von U(r) und beachtet, dass ∇ in
sphärischen Polarkoordinaten durch
1 ∂ 1 ∂
∂
∇ ≡ ∇r , ∇φ , ∇θ =
,
,
∂r r sin θ ∂φ r ∂θ
gegeben ist, dann folgt für E = −∇U(r)
Q
Q
Eaußen (x) = 2 êr .
Einnen (x) = 3 r êr ,
R
r
Das Feld E ist radial nach außen gerichtet, sein Betrag E(r) = |E| ist in
Abb. 1.1 aufgetragen. Im Außenraum ist dies das bekannte elektrische
Feld um die Punktladung Q, das mit dem inversen Quadrat des Radius
abklingt. Im Innenraum wächst oder fällt (je nach Vorzeichen von Q)
das Feld linear von Null im Ursprung auf den Wert Q/R2 bei R.
Bildet man in diesem Beispiel die Divergenz von E, so folgt mit
1 d
2 d U(r)
r
U(r) = 2
dr
r dr
sowohl im Innen- als auch im Außenbereich
div E = ∇ · E = −U(r) = 4π(r) .
Das ist natürlich nichts Anderes als die Poisson-Gleichung, die wir
in Abschn. 1.7 ausführlicher diskutieren, hier im Gauß’schen Maßsystem notiert.
Beispiel 1.3
Vektorpotential eines magnetischen Dipols: Es sei das statische Vektorfeld
m×x
A(x) =
,
(r = |x|) ,
r3
5
6
1
Die Maxwell’schen Gleichungen
Abb. 1.1. Der Betrag E(r) des elektrischen Feldes E(x) = E(r) êr für die
homogene Ladungsverteilung mit Radius R
1
E(r)/E(R)
0.5
0
1
2
3
x=r/R
4
gegeben, wo m ein konstanter Vektor ist. Es soll B = rot A berechnet
werden. Als Beispiel sei hier die 1-Komponente angegeben:
∂
∂
A3 (x) − 3 A2 (x)
2
∂x ∂x
3 1
∂
m1x2 − m2x1
∂
m x − m1 x3
= 2
− 3
∂x
r3
∂x
r3
1
m
3
= 2 3 + 5 −m 1 (x 2 )2 + m 2 x 1 x 2 + m 3 x 1 x 3 − m 1 (x 3 )2
r
r
m 1 3x 1 1 1
= − 3 + 5 m x + m2 x2 + m3 x3
r
r
1
1
= 3 −m + 3(x̂ · m)x̂1 ,
r
B1 (x) =
wobei im vorletzten Schritt ein Term 3m 1 (x 1 )2 /r 5 addiert und subtrahiert und x̂ = x/r eingesetzt wurden. Das Ergebnis ist somit
1
B(x) = 3 3(x̂ · m)x̂ − m .
r
Wenn m ein statischer magnetischer Dipol ist, dann beschreibt B(x) das
Induktionsfeld im Außenraum, das von diesem erzeugt wird.
1
1.2 Die Integralsätze im Fall des Ê 3
1.2 Die Integralsätze im Fall des R3
In einer auf dem Raum R3 zulässigen einfachen Notation lauten die
wichtigsten Integralsätze, auf denen die Elektrodynamik aufbaut, folgendermaßen:
Gauß’scher Satz
Es sei F eine glatte, orientierbare, geschlossene Fläche, die in den
R3 eingebettet ist und die ganz im Endlichen liegt. Es sei V(F) das
von dieser Fläche eingeschlossene Volumen und es sei V ein glattes
Vektorfeld. Dann gilt
3
d x ∇·V =
dσ V · n̂ .
(1.6)
F
V(F)
Hierbei ist n̂ die nach außen gerichtete Flächennormale am Ort des
Flächenelements dσ.
Die Relation (1.6) verknüpft das Volumenintegral der Divergenz
eines Vektorfeldes mit dem Integral seiner nach außen gerichteten Normalkomponente über die Fläche, die das Volumen einschließt. Dabei
kommt es nicht darauf an, ob V statisch, d. h. nur von x abhängig oder
nichtstatisch, d. h. eine Funktion V(t, x) der Zeit und des Ortes ist. Man
kann sich die rechte Seite von (1.6) als die Bilanz einer Strömung durch
die Fläche F hindurch vorstellen, die durch die Normalkomponente von
V gegeben ist. Die Divergenz im Integranden der linken Seite ist so
etwas wie eine ,,Quellstärke“, die diesen Fluss füttert. Hier folgt ein
Beispiel für die Anwendung des Gauß’schen Satzes.
Beispiel 1.4
Elektrisches Feld der homogenen Ladungsverteilung. Die Ladungsverteilung sei kugelsymmetrisch und homogen, (x) = 3Q/(4πR3 )
Θ(R − r). Die Divergenz des elektrischen Feldes ist proportional zur Ladungsdichte, ∇ · E = 4π. Da keine Richtung ausgezeichnet ist, kann
das Feld nur in die radiale Richtung zeigen, muss also die Form
E = E(r)êr haben. Setzt man diesen Ansatz anstelle von V in den
Gauß’schen Satz ein und wählt für F die Sphäre Sr2 mit Radius r um
den Ursprung, so gibt die rechte Seite von (1.6) die skalare Funktion
E(r) mal dem Flächeninhalt der Sr2 , d. h. E(r)4πr 2 . Auf der linken Seite
macht man die Fallunterscheidung
rR:
4π
r
3Q
d x (r) = (4π) r 2 dr Θ(R − r )
4πR3
3
2
0
Q
= 4π 3 r 3 ,
R
7
8
1
Die Maxwell’schen Gleichungen
r>R:
S r2
ρ (r) ≠ 0
r
R
4π
d3 x (r) = 4πQ .
Der Vergleich mit der rechten Seite ergibt das aufgrund des Beispiels 1.2
erwartete Resultat
Q
Q
E außen (r) = 2 , (E = E(r)êr ) .
E innen (r) = 3 r ,
R
r
Abbildung 1.2 illustriert die Geometrie dieses einfachen Beispiels.
Stokes’scher Satz
Abb. 1.2. Um das Symmetriezentrum
einer kugelsymmetrischen Ladungsverteilung (r) legt man z. B. eine Sphäre
Sr2 und integriert (r) über das von ihr
eingeschlossene Volumen. Das elektrische Feld auf Sr2 ist radial gerichtet und
folgt aus dem Gauß’schen Satz
Es sei C ein glatter, geschlossener Weg und es sei F(C) eine von
C begrenzte, ebenfalls glatte (orientierbare) Fläche. Für ein glattes
Vektorfeld V, das auf F inklusive seines Randes definiert ist, gilt
dσ ∇ × V · n̂ = ds · V .
(1.7)
F(C)
C
Hierbei ist n̂ die orientierte Flächennormale auf F(C), ds ist das gerichtete Linienelement auf C. Diese Orientierungen sind so korreliert,
dass die geschlossene Kurve C und n̂ eine Rechtsschraube bilden.
Bemerkungen
1. Für die Gültigkeit des Gauß’schen Satzes genügt es zu fordern, dass
die Fläche F, die das Volumen V(F) berandet, stückweise glatt sei.
Sie kann also beispielsweise wie die Oberfläche eines Fußballs aussehen: die Fläche ist überall stetig und besteht aus endlich vielen,
glatten Teilstücken. Auch im Stokes’schen Satz kann man zulassen,
dass die Randkurve C nur stückweise glatt ist.
2. Beiden Integralsätzen (1.6) und (1.7) ist gemeinsam, dass sie ein Integral über eine kompakte Mannigfaltigkeit M mit Rand mit einem
Integral über deren Rand verknüpfen, den man in der Differentialgeometrie mit ∂M bezeichnet. Im Gauß’schen Satz ist M ein
kompaktes Gebiet V(F) im R3 , ∂M ist seine Oberfläche F. Im Stokes’schen Satz ist M eine zweidimensionale, in den R3 eingebettete,
berandete Fläche, ∂M ist deren Randkurve. Außerdem erscheint im
Integral über ∂M eine Funktion des Vektorfeldes V, im Integral über
M erscheint dagegen eine Funktion der ersten Ableitungen von V,
einmal die Divergenz im Gauß’schen Satz, das andere Mal die Rotation im Stokes’schen Satz. In Tat und Wahrheit handelt es sich
bei (1.6) und (1.7) um ein und denselben Satz, wenn auch für unterschiedliche Dimensionen von M. In Abschn. 2.1.2 wird man sehen,
dass dieser wichtige Integralsatz in der Sprache der äußeren Formen allgemein, d. h. für jede Dimension n formuliert werden kann.
Er sagt, um dies hier vorweg zu nehmen, folgendes: Ist ω eine
1
1.2 Die Integralsätze im Fall des Ê 3
(n − 1)-Form mit kompaktem Träger auf der orientierten, berandeten Mannigfaltigkeit M definiert und übernimmt man die dadurch
induzierte Orientierung für ihren Rand ∂M, so gilt
⎛
⎞
⎞
⎛
⎟
⎜ ⎜
⎟
dω = ⎜
··· ⎟
⎝
⎠
⎟
⎜ ⎟
⎜
··· ⎟
⎜
⎠
⎝
(n)
M
(n−1)
ω,
∂M
oder, etwas kompakter geschrieben
dω = ω .
M
(1.8a)
(1.8b)
∂M
Im Satz (1.6) ist ω eine 2-Form, dω eine 3-Form, im Satz (1.7) ist ω
eine Einsform, ihre äußere Ableitung dω eine 2-Form. Mehr davon
in Abschn. 2.1.2!
3. Hier kommt ein besonders einfaches Beispiel für den Stokes’schen
Satz: Die Mannigfaltigkeit sei eine glatte Kurve M = γ , die von a
nach b läuft, ω sei eine Funktion oder, in der Sprache der äußeren
Formen, eine Nullform, ω = f . Der Rand ∂M von M besteht aus den
Punkten a und b, ∂M = {a, b}, und dω = d f ist das totale Differential von f . Aus der allgemeinen Form (1.8b) zurück übersetzt lautet
der Stokes’sche Satz hier
b
df
d f = dt
f,
= f(b) − f(a) =
dt
M=γ
∂M
a
wovon der mittlere Teil wohlvertraut ist.
Green’sche Sätze
Der Gauß’sche Satz (1.6) hat zwei Varianten, die u. A. bei der Diskussion von Randwertproblemen im R3 von großem Nutzen sind.
Erster Green’scher Satz
Es seien Φ(t, x) und Ψ(t, x) im Argument x C 2 -Funktionen. Es sei
V(F) ein endliches Volumen und F ≡ ∂V seine Oberfläche wie im
Gauß’schen Satz. Dann gilt
∂Ψ
3
.
(1.9)
d x ΦΨ + ∇Φ · ∇Ψ =
dσ Φ
∂ n̂
V(F)
F
Dieser Satz ist eine direkte Anwendung des Gauß’schen Satzes (1.6),
wenn man dort das Vektorfeld
V(t, x) = Φ(t, x) (∇Ψ(t, x))
9
10
1
Die Maxwell’schen Gleichungen
einsetzt und die Produktregel für die Differentiation verwendet,
∇ · Φ∇Ψ = ∇Φ · ∇Ψ + ΦΨ .
Notiert man den Satz (1.9) mit den Funktionen Φ und Ψ vertauscht und
subtrahiert man die beiden so erhaltenen Formeln voneinander, dann erhält man den zweiten Green’schen Satz:
Zweiter Green’scher Satz
Unter denselben Voraussetzungen wie im Gauß’schen Satz gilt
∂Φ
∂Ψ
3
−Ψ
.
(1.10)
d x ΦΨ − Ψ Φ =
dσ Φ
∂ n̂
∂ n̂
V(F)
F
In beiden Fällen ist mit ∂Ψ/∂ n̂ bzw. ∂Φ/∂ n̂ die Normalableitung gemeint, das ist die Richtungsableitung der jeweiligen Funktion in Richtung der Flächennormalen n̂ am betrachteten Punkt der Fläche F, die
auch anders als n̂ · ∇Ψ bzw. n̂ · ∇Φ geschrieben werden kann.
1.3 Maxwell’sche Gleichungen in integraler Form
Dieser Abschnitt fasst die Maxwell’schen Gleichungen in der integralen
Form zusammen, wie sie in makroskopischen Experimenten ganz unterschiedlicher Art direkt und indirekt getestet oder angewandt werden.
Ich setze voraus, dass der Leser/die Leserin die wichtigsten Experimente
zur klassischen Elektrodynamik und die daraus zu ziehenden Schlüsse
schon von Schulzeiten her oder aus Vorlesungen über Experimentalphysik kennen.
1.3.1 Das Induktionsgesetz
Es sei C eine glatte Kurve endlicher Länge, ds das Linienelement entlang dieser Kurve und sei E(t, x) ein elektrisches Feld. Dann nennt man
das Wegintegral C ds · E(t, x) die elektromotorische Kraft.
Sei nun ein magnetisches Induktionsfeld B(t, x) vorgegeben, das sowohl zeitlich als auch räumlich veränderlich sein darf, und sei C eine
glatte, jetzt aber geschlossene Kurve im R3 , die eine glatte Fläche F
berandet. Sowohl die Fläche F als auch ihre Randkurve C können
durchaus zeitlich veränderlich sein, allerdings sollen alle Änderungen
mindestens stetig, oder sogar ihrerseits glatt sein. Die Fläche soll orientiert sein, die lokale Flächennormale sei mit n̂(t, x) bezeichnet. Dann
ist der magnetische Fluss durch die Fläche F als das Flächenintegral