6.2.13 Ein- und Ausschaltvorgang am Kondensator
Werbung
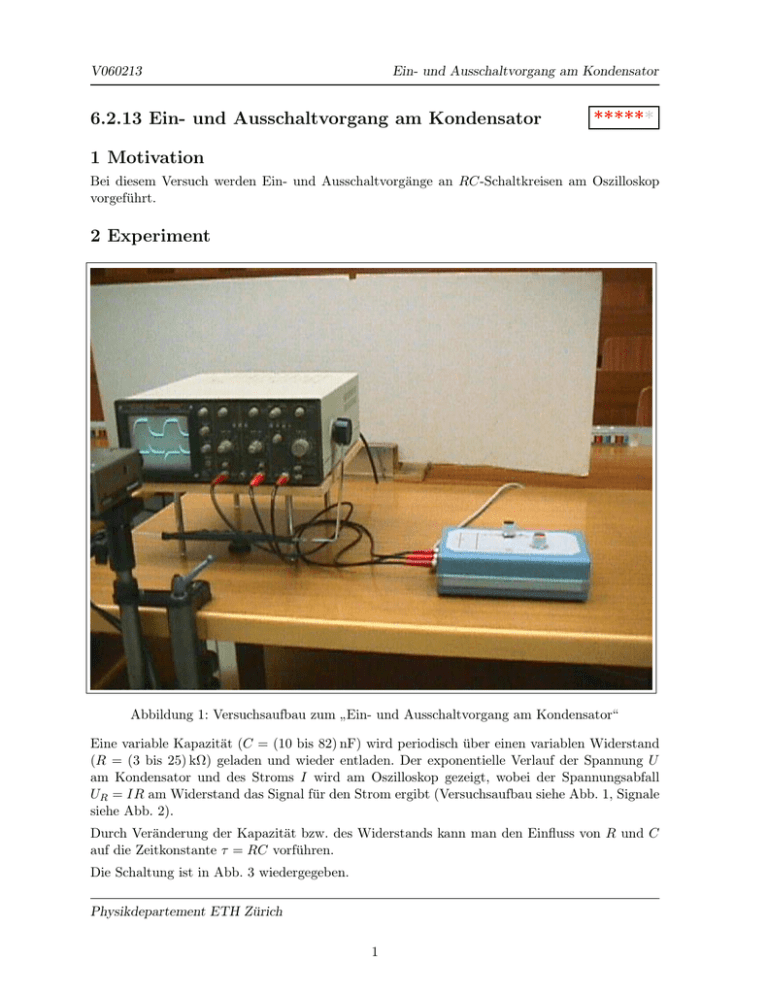
V060213 Ein- und Ausschaltvorgang am Kondensator 6.2.13 Ein- und Ausschaltvorgang am Kondensator ****** 1 Motivation Bei diesem Versuch werden Ein- und Ausschaltvorgänge an RC-Schaltkreisen am Oszilloskop vorgeführt. 2 Experiment Abbildung 1: Versuchsaufbau zum Ein- und Ausschaltvorgang am Kondensator“ ” Eine variable Kapazität (C = (10 bis 82) nF) wird periodisch über einen variablen Widerstand (R = (3 bis 25) kΩ) geladen und wieder entladen. Der exponentielle Verlauf der Spannung U am Kondensator und des Stroms I wird am Oszilloskop gezeigt, wobei der Spannungsabfall UR = IR am Widerstand das Signal für den Strom ergibt (Versuchsaufbau siehe Abb. 1, Signale siehe Abb. 2). Durch Veränderung der Kapazität bzw. des Widerstands kann man den Einfluss von R und C auf die Zeitkonstante τ = RC vorführen. Die Schaltung ist in Abb. 3 wiedergegeben. Physikdepartement ETH Zürich 1 V060213 Ein- und Ausschaltvorgang am Kondensator Laden Entladen Laden Entladen U 0 I 0 t Abbildung 2: Strom und Spannung beim Laden und Entladen eines Kondensators 3 Theorie 3.1 Die Kirchhoffschen Gesetze Häufig müssen in einem komplizierteren Netzwerk die Ströme, Spannungen, Leistungen berechnet werden. Dazu werden die Kirchhoffschen Gesetze verwendet: A) Die Summe aller Ströme eines Stromknotens ist 0: n X Ii = 0 (1) i=1 Hierbei werden zufliessende Ströme positiv und abfliessende Ströme negativ gerechnet (Ladungserhaltung). B) In einem geschlossenen Kreis ist die Summe der an den einzelnen Elementen liegenden Spannungen gleich gross wie die Summe der Batteriespannungen . Bei komplizierteren Problemen liefert das folgende Verfahren ein Minimum an Gleichungen (und damit an Rechenarbeit !): Physikdepartement ETH Zürich 2 V060213 Ein- und Ausschaltvorgang am Kondensator UR = IR 1 2 S1 R + UC C − I Abbildung 3: RC-Schaltkreis. Der Schalter S1 bewirkt in Stellung 1 das Laden und in Stellung 2 das Entladen des Kondensators. a) Man führe als Unbekannte die Spannungen Ui bezüglich eines Fixpunktes ( = Spannungen gegen Erde) in den Knoten ein. b) Man schreibe die Stromerhaltung für die Netzwerkknoten auf, wobei die Ströme durch die unbekannten Spannungen und die Widerstandswerte auszudrücken sind. c) Die Lösung dieses (linearen !) Gleichungssystems liefert die Unbekannten Ui . Aus diesen können alle andern Grössen leicht berechnet werden. Für n Widerstände Ri , i = 1, ..., n) in Serie gilt für den resultierenden Gesamtwiderstand R: R= n X Ri (2) i=1 Bei Parallelschaltung dieser Widerstände gilt dagegen: n X 1 1 = R Ri (3) i=1 3.2 Lade – und Entladevorgang beim RC-Kreis Wir untersuchen den Lade – und den Entladevorgang für den RC-Kreis. a) Ladevorgang: Nach Kirchhoff gilt (siehe Abb. 3) U0 = UR + UC = IR + Physikdepartement ETH Zürich 3 Q C (4) V060213 Ein- und Ausschaltvorgang am Kondensator Beim Aufladen des Kondensators ist Q̇ = I ⇒ ⇒ U0 = RQ̇ + (5) Q C (6) dQ U0 Q = − dt R RC (7) Mit dem Ladestrom I0 := U0 /R zu Beginn des Aufladens und der Zeitkonstanten τ = RC erhalten wir schliesslich die Differentialgleichung dQ Q = I0 − dt τ (8) dQ dt =− Q − τ I0 τ (9) Die Separation der Variablen ergibt t ln(Q − τ I0 ) = − + c1 τ ⇒ Q = τ I0 + c2 e−t/τ ⇒ (10) (11) Für t = 0 ist Q = 0. Daraus folgt die Integrationskonstante c2 ≡ ec1 und die Ladung Q = Q(t): 0 = τ I0 + c2 ⇒ (12) c2 = −τ I0 Q = τ I0 1 − e−t/τ (13) (14) Der Ladestrom ergibt sich damit zu I = Q̇ = I0 e−t/τ (15) Die Spannung am Kondensator ist gegeben durch U= Q τ I0 = 1 − e−t/τ = U0 1 − e−t/τ C C (16) Der Verlauf von U und I in Funktion der Zeit ist für τ = 800 ms in Abb. 4 zu sehen. b) Entladevorgang: Nach Kirchhoff gilt (siehe Abb. 2) 0 = UR + UC = IR + Q C Beim Entladen des Kondensators ist die Spannungsquelle abgetrennt, und es ist Physikdepartement ETH Zürich 4 (17) V060213 Ein- und Ausschaltvorgang am Kondensator Q̇ = I ⇒ (18) 0 = RQ̇ + Q C (19) Damit erhalten wir schliesslich die Differentialgleichung dQ Q =− dt τ (20) Die Separation der Variablen ergibt in diesem Fall dQ dt =− Q τ ⇒ (21) t ln Q = − + c1 τ ⇒ Q = c2 e−t/τ (22) (23) Für t = 0 ist Q = CU0 . Daraus folgt die Integrationskonstante c2 ≡ ec1 und die Ladung Q = Q(t): CU0 = c2 (24) −t/τ Q = CU0 e −t/τ = τ I0 e (25) Der Strom ergibt sich damit zu I = Q̇ = −I0 e−t/τ (26) Die Spannung am Kondensator ist gegeben durch U= Q = U0 e−t/τ C Der Verlauf von U und I in Funktion der Zeit ist für τ = 800 ms in Abb. 4 zu sehen. Physikdepartement ETH Zürich 5 (27) V060213 Ein- und Ausschaltvorgang am Kondensator 1,0 0,8 U/U0 = 1 − e−t/τ 0,6 Laden 0,4 I/I0 = e−t/τ 0,2 t/s 0,0 0 1 2 3 4 5 1,0 0,8 0,6 0,4 U/U0 = e−t/τ 0,2 0,0 -0,2 I/I0 = −e−t/τ -0,4 Entladen -0,6 -0,8 t/s -1,0 0 1 2 3 4 5 Abbildung 4: Strom- und Spannungsverlauf beim Laden (oberes Bild) und Entladen (unteres Bild) eines Kondensators (τ ≡ RC = 0,8 s). Physikdepartement ETH Zürich 6











