Cournot-Modell

Cournot-Modell
Cournots Modell ist ein Oligopolmodell mit Mengenwahl. Es wird
hier mit 2 Firmen dargestellt, also als Duopol.
Firmen entscheiden über Produktionsmenge, die sie auf den Markt
bringen; Preis bildet sich entsprechend der Nachfrage, gegeben die
Gesamtmenge am Markt
Gewinn:
Π1 (x1 , x2 ) = p(x1 + x2 )x1 − C (x1 )
p(X ) ist die inv. Nachfragefkt., X = x1 + x2 Marktoutput, Kosten
hängen natürlich nur von eigener Produktion x1 ab; linearer Fall:
Π1 (x1 , x2 ) = (a − b(x1 + x2 )) x1 − c1 x1
1 / 42
Reaktionsfunktion
Was ist die b.A. von x1 auf x2 , um Π1 möglichst groß zu machen?
x1R (x2 ) = arg max Π(x1 , x2 )
x1
Erlös: R(x1 , x2 ) = p (X (x1 , x2 )) x1 , Grenzerlös:
∂R(x1 , x2 )
dp ∂X
= p + x1
∂x1
dX ∂x1
wobei
∂X
∂(x1 + x2 )
∂x1 ∂x2
=
=
+
=1+0
∂x1
∂x1
∂x1 ∂x1
die Outputerhöhung von U2 ist Null, da U2 im simultanen
Wettbewerb nicht auf x2 reagieren kann
2 / 42
Reaktionsfunktionen im Linear-Linearen Fall
∂Π1
!
= (a − b(x1 + x2 )) + x1 (−b) − c1 = 0 ⇒
∂x1
a − c1 x2
x1R (x2 ) =
−
und wegen der Symmetrie,
2b
2
a − c2 x1
x2R (x1 ) =
−
2b
2
d.h. wenn U1 erwartet, dass U2 seine Menge um eine Einheit
erhöht, dann sinkt die gewinnmaximierende Menge von U1 um 0,5
Einheiten
dx1R /dx2 = −
1
2
3 / 42
Darstellung der Reaktionsfunktionen und des
Cournot-Nash-Gleichgewichts (CNG)
am Bsp. c1 = c2 = c:
alle Punkte auf den beiden Geraden sind b.A., aber nur ein Punkt
ist eine Strategiekombination, die eine wechselseitige b.A..
darstellt; der Schnittpunkt ist daher das (einzige) CNG
4 / 42
Schnittpunkt
Schnittpunkt x1R (x2 ) = x2R (x1 ):
x1C =
3 C
x =
4 1
x1C =
x2C =
=
=
=
a − c1 1 a − c2 1 C
−
− x1
2b
2
2b
2
2a − 2c1 − a + c2
4b
1
(a − 2c1 + c2 )
3b
a − c2 1 1
−
(a − 2c1 + c2 )
2b
2 3b
3a − 3c2 − a + 2c1 − c2
6b
2a − 4c2 + 2c1
6b
1
(a − 2c2 + c1 )
3b
muss auch analog ausschauen wegen Symmetrie
5 / 42
Lösung der Restlichen Variablen
X C = x1C + x2C =
1
(2a − c1 − c2 )
3b
1
p C = (a + c1 + c2 )
3
1
C
Π1 =
(a − 2c1 + c2 )2
9b
1
ΠC2 =
(a − 2c2 + c1 )2
9b
man sieht auch: ∂ΠCi /∂a > 0, und ∂ΠCi /∂b < 0, d.h. Erhöhung
der Zahlungsbereitschaft wirkt sich positiv auf die Gewinne aus;
Anwendung: eine koordinierte industrieweite Werbekampagne kann
zu einer Erhöhung von a oder Senkung von b führen und für alle
Produzenten lohnen (z.B. Fleisch bringts”-Werbung der AMA)
”
6 / 42
Kostenführerschaft
direkter Weg: senke c1 , z.B. durch F&E (s. Kap. G und H)
indirekter Weg: erhöhe c2 , die Kosten des Konkurrenten; z.B.
Erhöhung der Umweltschutzvorschriften in China
7 / 42
EINSCHUB ANFANG: Direkte und Indirekte Effekte
Betrachten ein allgemein gehaltenes zweistufiges Spiel für zwei
Firmen; beide entscheiden über Kaptialeinsatz (K1 , K2 ) in der
ersten Stufe und (x1 , x2 ) Produktionsmengen in der zweiten Stufe;
auf jeder Stufe erfolgen die Entscheidungen simultan
Gewinne der Unternehmen sind wieder vom Verhalten des anderen
abhängig:
Π1 (K1 , K2 , x1 , x2 ), Π2 (K1 , K2 , x1 , x2 ).
es gibt unendlich viele Teilspiele, weil Ki und xi kontinuierlich sind
eine Strategie von U1 ist (K1 , x1 ), mit x1 = x1 (K1 , K2 );
8 / 42
Zweistufiges Spiel für Firmen
Rückwärtsinduktion ist wieder möglich:
1. löse das letzte Teilspiel, also Stufe 2 :
bestimme x1N (K1 , K2 ) und x2N (K1 , K2 ), opt. Menge ∀ (K1 , K2 ), als
Lösung der FOC:
∂Π1 (K1 , K2 , x1 , x2 )
= 0,
∂x1
∂Π2 (K1 , K2 , x1 , x2 )
= 0.
∂x2
9 / 42
Zweistufiges Spiel für Firmen
2. löse das erste Teilspiel, also Stufe 1 :
bestimme durch Einsetzen
N
N
ΠN
1 (K1 , K2 ) = Π(K1 , K2 , x1 (K1 , K2 ), x2 (K1 , K2 )),
N
N
ΠN
2 (K1 , K2 ) = Π(K1 , K2 , x1 (K1 , K2 ), x2 (K1 , K2 )).
Ki kann jetzt in Antizipation von xi (K1 , K2 ) gewählt werden; das
spiegelt sich in FOC auf erster Stufe (erstes Teilspiel) wieder:
∂Π1 (·)
∂Π1 ∂Π1 ∂x1N
∂Π1 ∂x2N
=
+
+
= 0,
∂K1
∂K1
∂x1 ∂K1
∂x2 ∂K1
∂Π2 (·)
∂Π2 ∂Π2 ∂x2N
∂Π2 ∂x1N
=
+
+
= 0.
∂K2
∂K2
∂x2 ∂K2
∂x1 ∂K2
de facto entscheidet sich das Spiel auf der ersten Stufe, da die
Auswirkung der Aktion auf der ersten Stufe schon die zweite Stufe
berücksichtigt
10 / 42
Effekte einer Veränderung auf Stufe 1
die Veränderung von ΠN
1 (K1 , K2 ) durch K1 kann in zwei Effekte
unterschieden werden:
∂Π1 ∂Π1 ∂x1N
∂Π1 ∂x2N
∂Π1 (·)
=
+
+
= 0,
∂K1
∂K1
∂x1 ∂K1
∂x2 ∂K1
1. direkter Effekt: Π ändert sich direkt durch K1 , auch wenn x1
und x2 konstant gehalten werden
2. indirekter Effekt: Π ändert sich durch K1 über x1N (K1 , K2 ) und
x2N (K1 , K2 ); auch genannt strategischer Effekt”
”
11 / 42
Effekte einer Veränderung auf Stufe 1; EINSCHUB ENDE
das Envelope-Theorem besagt, dass einer der indirekten Effekte:
∂Π1 ∂x1N
∂x1 ∂K1
bei ganz kleinen” Veränderungen von K1 0 ist
”
Begründung: x1 wurde bereits für Stufe 2 so gewählt, dass
N
Π1 = ΠN
1 ist, nämlich x1 ; in anderen Worten, x1 wurde auf Stufe 2
so gewählt, dass gilt (s. Lösung auf Stufe 2, oben):
∂Π1 /∂x1 = 0
setzt man das ein, verschwindet der mittlere Summand (in der
vorherigen Folie) bei kleinen Änderungen von K1 ; denn x1N ist bei
K1 optimal, und wenn sich K1 wenig verändert, verändert sich auch
x1 nur wenig”, und dann ist die Auswirkung auf den Profit null
”
12 / 42
Direkter Weg
Fortsetzung mit dem direkten Weg der Kostenführerschaft; c1 wird
vielleicht direkt gewählt (F&E-Ausgaben), vielleicht durch einen
exogenen Schock“ verändert (Umweltstandards); reduzierte
”
CNG-Gewinnfkt:
ΠC1 (c1 , c2 ) = Π1 (c1 , c2 , x1C (c1 , c2 ), x2C (c1 , c2 ))
Effekt:
∂Π1 ∂Π1 ∂x1C
∂Π1 ∂x2C
∂ΠC1
=
+
+
<0
∂c1
∂c1
∂x1 ∂c1
∂x2 ∂c1
|{z}
|{z}
|{z}
|{z}
<0
=0
<0
>0
| {z }
<0
dir. Effekt (erster Summand) negativ: Reduktion der Stückkosten
(eigener) indir. Effekt Null (wegen Envelope-Theorem)
strategischer Effekt” negativ: zweiter Faktor positiv, b.A. von U2
”
fallend in c1 ; erster Faktor negativ, denn mit x2 fällt der Preis und
daher der Profit von U1 (gegeben ein beliebiges x1 )
13 / 42
Gesamteffekt
Reaktionsfunktionen bei Kostensenkung:
Investitionsanreiz zur Kostensenkung also über zwei Kanäle:
Verringerung der Produktionskosten, aber auch strategischer
Effekt, weil mehr angeboten wird nach der Kostensenkung
14 / 42
Indirekter Weg
Veränderung der reduzierten Gewinnfunktion durch Erhöhung der
Kosten des Konkurrenten:
∂Π1 ∂Π1 ∂x1C
∂Π1 ∂x2C
∂ΠC1
=
+
+
>0
∂c2
∂c2
∂x1 ∂c2
∂x2 ∂c2
|{z} |{z}
|{z} |{z}
=0
=0
<0
<0
| {z }
>0
dir. Effekt (erster Summand) Null: Kostenerhöhung von U2 hat
keinen direkten Effekt auf den Gewinn von U1
(eigener) indir. Effekt wieder Null (wegen Envelope-Theorem)
strategischer Effekt” positiv: zweiter Faktor negativ, höhere
”
Kosten c2 führen zu Senkung von x2 ; erster Faktor negativ, denn
geringeres x2 erhöht den Preis und daher den Profit von U1
15 / 42
Gewinn des Anderen bei Direkter Kostensenkung
vorherige Ableitung zeigt auch (durch Indexvertauschung) dass Π2
verringert wird wenn c1 sinkt:
∂Π2 ∂Π2 ∂x2C
∂Π2 ∂x1C
∂ΠC2
=
+
+
>0
∂c1
∂c1
∂x2 ∂c1
∂x1 ∂c1
|{z}
|{z}
|{z}
|{z}
=0
=0
<0
<0
| {z }
>0
die Reaktionsfunktionen bei indirekter Kostenführerschaft von U1:
16 / 42
Randlösung
Angebot von U2 von Null bei:
a − c2 x1
−
=0⇒
2b
2
a − c2
= x1LC
x1 =
b
x2R (x1 ) =
das macht Sinn wenn man auf den Preis in dieser Situation schaut:
a − c2
LC
p(x1 ) = a − b
2b
= a − a + c2 = c2
d.h. x1 ≥ x1LC führt zu p ≤ c2 , wodurch Π2 ≤ 0 und die b.A. ist
x2R (x1LC ) = 0
17 / 42
Vollständige Reaktionsfunktion
präziser als oben schreibt man daher:
a−c2 x1
R
2b − 2 ,
x2 (x1 ) =
0,
2
x1 < a−c
b
sonst
und graphisch:
die b.A. von U1 auf x2 = 0 ist natürlich die Lösung ds
Monopolisten
18 / 42
Blockierter Markteintritt
wenn x1M ≥ x1LC , dann kann U1 Monopolist sein und U2 nicht
eintreten:
wie groß die Grenzkosten c2 dafür sein müssen, sieht man am
Vergleich der Mengen (Intuition in letzter Zeile bestätigt):
a − c1
a − c2
x1M =
≥
= x1LC
2b
b
a − c1 ≥ 2a − 2c2
1
c2 ≥ (a + c1 ) = p1M
2
19 / 42
Markteintritt und Marktstruktur im Cournot-Wettbewerb
graphische Zusammenfassung von Cournot-Duopol und Blockade:
20 / 42
Stackelberg-Modell
Modell des sequentiellen Mengenwettbewerbs, von Stackelberg
(1934); erster Duopolist wählt Menge, ist der
Stackelberg-Führer”, Zweier, der Stackelberg-Folger”,
”
”
beobachtet das, und antwortet mit seiner Menge, aber jetzt nicht
simultan sonder in Zeitperiode zwei:
Gewinnfunktionen wie bei Cournot, aber Lösung jetzt durch
Rückwärtsinduktion; zweite Stufe bleibt gleich:
x2R (x1 ) = arg max Π2 (x1 , x2 ) =
x2
a − c2 1
− x1
2b
2
21 / 42
Erste Stufe des Führers
Stackelberg-Führer kann x2 beeinflußen und sich aus x2R (x1 ) ein x2
aussuchen; d.h. er berücksichtigt seinen Einfluß auf x2 explizit:
Π1 x1 , x2R (x1 ) = p x1 + x2R (x1 ) x1 − c1 x1
im linear-linearen Fall:
Π1
x1 , x2R (x1 )
=
a − b x1 +
a − c2 1
− x1
2b
2
− c1 x1
1
= (a − bx1 + c2 − 2c1 )x1
2
1
1
!
dΠ1 /dx1 = (−b)x1 + (a − bx1 + c2 − 2c1 ) = 0 ⇒
2
2
a + c2 − 2c1
x1S =
2b
22 / 42
Lösung Graphisch und Vergleich Cournot
beachte: x1R (x2 ) ist für Stackelberg-Modell unbedeutend; in
Cournot ist x1S nicht b.A. auf x2S , aber in Stackelberg-Modell
trotzdem optimal; Grund: x1R (x2 ) berücksichtigt nicht dass U2 bei
x1R (x2S ) abweichen wird von x2S
23 / 42
Lösung Restliche Variablen
Lösungen für (x1S , x2R ):
x1S =
x2S =
XS =
p(X S ) =
ΠS1 =
ΠC2 =
a − 2c1 + c2
2b
a + 2c1 − 3c2
4b
3a − 2c1 − c2
4b
1
(a + 2c1 + c2 )
4
1
(a − 2c1 + c2 )2
8b
1
(a − 3c2 + 2c1 )2
16b
24 / 42
Strategische Handelspolitik
Anwendung des Cournot-Wettbewerbs; Staat d (domestic) und
Staat f (foreign) produzieren für Staat k; Staat d hat eine Idee,
und überlegt sich: können wir das Unternehmen Ud
”
subventionieren und damit eine Verbesserung der Wohlfahrt
erreichen?”, also
ΠCd (c − s, c) − xdC (c − s, c) · s > ΠCd (c, c)
sei wieder cd = cf = c; Struktur:
25 / 42
Effekt
Subventionszahlungen gesamtwirtschaftlich neutral, da der Staat
bezahlt was sich Ud erspart; aber der Effekt einer direkten
Kostenführerschaft auf den Gewinn für Ud ist positiv (s. oben);
Staat d kann s so wählen, dass Πd maximal wird:
26 / 42
Stufe 1
auf der ersten Stufe ergibt sich die optimale Subvention, und damit
der Rest:
a−c
4
a − c + 2 a−c
a
−
c + 2s
a−c
4
xdC (c − s, c) =
=
=
3b
3b
2b
s=
als Resultat ist nach kurzer Reflexion nicht überraschend dass
xdC (c − s, c) = xdS (c, c)
denn da, wie festgestellt, die Subvention keine Kosten verursacht,
kann man die Menge gegeben xfR aussuchen, und kommt wieder
zur Stackelberg-Lösung; die Einführung der Subventionswahl
verwandelt das Cournot-Spiel in ein zweistufiges Stackelberg-Spiel
27 / 42
Beispiel und Diskussion
mögliches Beispiel: Boeing und Airbus;1 Airbus erhält hohe
Subventionen und wird dadurch vom Industrieneuling langsam zum
Marktführer; interessant, dass Airbus (im Fall von Gewinnen) die
Subventionen sogar zurückzahlen muss, d.h. der Staat hat keine
Kosten (außer Risiko)
Wie wäre es wenn sich ein Unternehmen selbst eine Subvention
zahlt?
1
Siehe Holmes, Stanley, Finally, a Boeing-Airbus Showdown, Business
Week, 7. Oktober 2004.
28 / 42
Kartellpolitik der Generaldirektion Wettbewerb der EU
Erklärung: Ein Kartell ist eine Gruppe von ähnlichen, unabhängigen
Unternehmen, die durch gemeinsame Absprache Preise festlegen,
die Produktionsmenge beschränken, oder Märkte untereinander
aufteilen.
Problem: Die Absprachen verringern die Anreize zur Verbesserung
von Produkten und Dienstleistungen und zum Angebot zu
kompetitiven Preisen. Daher zahlen ihre Abnehmer (Konsumenten
und andere Unternehmen) mehr für schlechtere Qualität.
Politische Konsequenz: Das ist der Grund dafür dass Kartelle nach
EU-Recht verboten sind und hohe Strafen verhängt werden.
29 / 42
Kronzeugenregelung
Kartelle sind aufgrund der strengen Geheimhaltung schwer zu
entdecken.
Daher gibt es die Kronzeugenregelung: das erste Unternehmen
eines Kartells, das der Europäischen Kommission Belege für ein
Kartell übergibt, muss keine Strafe zahlen. Die K. führt zur
Destabilisierung der Kartelle.
Die meisten Kartelle der letzten Jahre wurden durch einen K.
aufgedeckt.
Die Kommission unterhält aber auch ihre eigenen Untersuchungen
um Kartelle zu entdecken.
30 / 42
Kartellbeispiel 1
Kartell für Tiernahrung;2
I
sechs europäische Firmen: FR, FI, BE, ES, ES, PT
I
Kartell nachweisbar von März 1969 bis Februar 2004
I
beendet durch finnische Kemira, die durch
Kronzeugenregelung komplette Immunität erhalten hat
I
Kartellabsprachen: Aufteilung von Marktanteilen und bei
Bedarf Koordinierung von Preisen
I
Gesamtstrafen: 176 Millionen Euro
2
Siehe Tait, Nikki, EU fines six groups in animal feed cartel, Financial
Times, 21. Juli 2010.. Und: http://ec.europa.eu.
31 / 42
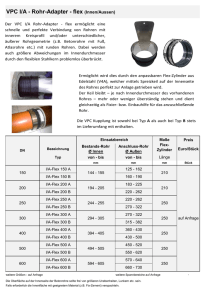
Kartellbeispiel 2
Kartell für Badezimmerausstattung (Sanitärkeramik: Waschbecken,
Badewannen, Armaturen, etv);3
I
I
I
I
I
I
17 Firmen: AT, IT, DE, US, ES, CH
Kartell nachweisbar von 1992 bis 2004
beendet durch US-amerikanische Masco (Kronzeugenregelung)
Kartellabsprachen: Treffen bei Fachverbandstagungen in
Deutschland (über 100 Treffen), Österreich (über 80), Italien
(65) sowie Belgien, Frankreich und den Niederlanden und
durch bilaterale Kontakte; dabei wurden Preiserhöhungen,
Mindestpreise und Rabatte festgesetzt und vertrauliche
Geschäftsinformationen ausgetauscht
Schaden für Bauunternehmen und Klempner, und letzten
Endes Konsumenten; aber natrürlich auch für Aktionäre,
Villeroy & Boch Aktien fielen um 1.24 Euro (24%)
Gesamtstrafen: 622 Millionen Euro
3
Siehe Bodoni, S., Moshinsky, B., Ideal Standard, Villeroy Fined on EU
Bathroom Cartel, Business Week, 23. Juni 2010. Und: http://ec.europa.eu.
32 / 42
Kartelle 2010
Markt
Strafe
Polyurethanschaum
Tiernahrung
176
Spannstahl
Badezimmerausstattung
622
Kohlenstofffreies Papier
21
Metallkomponenten von
Fenstern und Türen
Mai 2010
4 DRAM-Speicher
331
Mai 2010
3 Landwirtschaftliche Dehnfolien
Feb. 2010
2 Elektronische Fahrzeugtechnikteile
Feb. 2010
1 Flexible Wechselstromübertragungssysteme
Anm.: Strafen in Millionen Euro.
Quelle: http://ec.europa.eu/competition/cartels/cases/cases.html.
Aug.
Jul.
Jun.
Jun.
Jun.
Jun.
2010
2010
2010
2010
2010
2010
10
9
8
7
6
5
33 / 42
Kartelle 2009
Dez.
Nov.
Nov.
Okt.
Sep.
Sep.
Jul.
Jul.
Jul.
Jul.
Mar.
Feb.
Feb.
Jan.
Jan.
2009
2009
2009
2009
2009
2009
2009
2009
2009
2009
2009
2009
2009
2009
2009
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Markt
Bananenkartell
Computer- und Fernsehbildschirme
Hitzestabilisatoren für Plastik
Netztransformator
Hochbaubetonteile
Zementprodukte
Kalziumkarbid
LCD-Elemente
Gasmarkt
Spezialglas
Garnelen
Kühlkompressoren
Hochstromkabel
Chipkarten
Rohölschiffsschläuche
Strafe
173
68
83
61
553
131
Anm.: Strafen in Millionen Euro.
Quelle: http://ec.europa.eu/competition/cartels/cases/cases.html.
34 / 42
Kartell im Mengenmodell
Die Kartelllösung entspricht der Monopollösung; es könnte
höchstens sein, dass dies von den Kartellmitgliedern als zu
offensichtlich betrachtet würde.
Zu beachten sind:
I
nur Produktion zu niedrigst möglichen Grenzkosten ist
profitmaximierend
I
Kartellgewinn muß bei unterschiedlichen Grenzkosten so
aufgeteilt werden, dass die Anreize zur Kartellabsprache
erhalten bleiben
I
Kontroll- (zur schnellen Entdeckung eines
Abmachungsbruchs) und Sanktionsmechanismen (schwierig
bei Rechtswidrigkeit von Kartellen) können festgelegt werden
aber Einhaltung ist schwierig, wegen inhärenter Instabilität
35 / 42
Absprache und Abweichung Graphisch
keine einzige Outputkombination (außer die Randpunkte) die zur
Kartellmenge führt, liegt auf der Reaktionsfkt. auch nur eines
Unternehmens
36 / 42
Absprache und Abweichung
die Situation nach der Kartellabsprache ist ähnlich wie die des
Gefangenendilemmas:
U2
kooperiert betrügt
kooperiert
8, 8
6, 9
betrügt
9, 6
6, 6
U1
Bruch der Absprache ist eine schwach dominante Strategie; wird
eine solche Strategie gewählt (plausibel), dann ist die schlechteste
Situation erreicht (auch schlechter als das CNG)
Anmerkung: im linear-linearen Fall mit c1 = c2 = c entsprechen die
2
obigen Auszahlungen den Profiten wenn sie mit dem Faktor (a−c)
64b
multipliziert werden; die Mengen sind symmetrisch xikoop = 2 · a−c
8b
und xibetr = 3 · a−c
8b
37 / 42
Wettbewerbsintensität
die Abbildung zeigt das Marktangebot bei den verschiedenen
Fällen:
Läßt sich der Zusammenhang zwischen Marktstruktur und
Wettbewerbsintensität irgendwie einfach erfassen, etwa durch eine
einzelne Zahl? Oder anders herum: gegeben die üblichen einfachen
Konzentrationsmaße, welche Resultate erhält man für die
besprochenen theoretischen Modelle?
38 / 42
Konzentrationsrate
si ist Marktanteil von Firma i:
xi
X
Konzentrationsrate Ck ist der Marktanteil der k größten
Unternehmen:
si =
Ck =
k
X
si
i=1
Spezialfälle:
k
n
I
bei k gleich großen Unternehmen: Ck =
I
bei Monopol: C1 = 1
I
bei vollständiger Konkurrenz: limn→∞ kn = 0
Kritik: Konzentrationsrate verändert sich nicht durch Fusionen
unter den k größten Unternehmen
39 / 42
Hirschman-Herfindahl-Index (HHI)
Summe der quadrierten Marktanteile aller Unternehmen (HHI oder
H):
H=
n X
xi 2
i=1
X
=
n
X
si2
i=1
Spezialfälle:
I
bei n gleich großen Unternehmen:
2 P
2
P H = ni=1 XX/n = ni=1 n1 = n n12 =
1
n
I
bei Monopol: H = 1
I
bei vollständiger Konkurrenz: limn→∞ n1 = 0
40 / 42
Hirschman-Herfindahl-Index
fortgesetzt
H hängt von Anzahl der Unternehmen und von Verteilung der
Marktanteile ab; das läßt sich ausdrücken durch die Umformung zu
q P
n
1
2
2
i=1 (xi − X /n)
1+V
n
mit V =
H=
n
X /n
V wird Variationskoeffizient” genannt und ist definert als
”
Standardabweichung dividiert durch den Mittelwert; es handelt sich
also um V der Produktionsmengen
41 / 42
Wettbewerbsrecht
PW illustrieren die Stellung dieser Maße im deutschen
Wettbewerbsrecht:
So wird etwa nach Par. 19 (3) GWB (Gesetz gegen
Wettbewerbsbeschränkungen) vermutet, dass ein Unternehmen
”
marktbeherrschend ist, wenn es einen Marktanteil von mindestens
einem Drittel hat. Eine Gesamtheit von Unternehmen gilt als
marktbeherrschend, wenn sie
1. aus drei oder weniger Unternehmen besteht, die zusammen
einen Marktanteil von 50 vom Hundert erreichen oder
2. aus fünf oder weniger Unternehmen besteht, die zusammen
einen Marktanteil von zwei Dritteln erreichen [...]”
Urteile auf Basis dieser Maße sind aber nicht sinnvoll, aber hilfreich
zum Screening” der Industrien und ihrer Unternehmen und als
”
Anlaß, genauere Untersuchungen vorzunehmen
42 / 42