Rechenwege

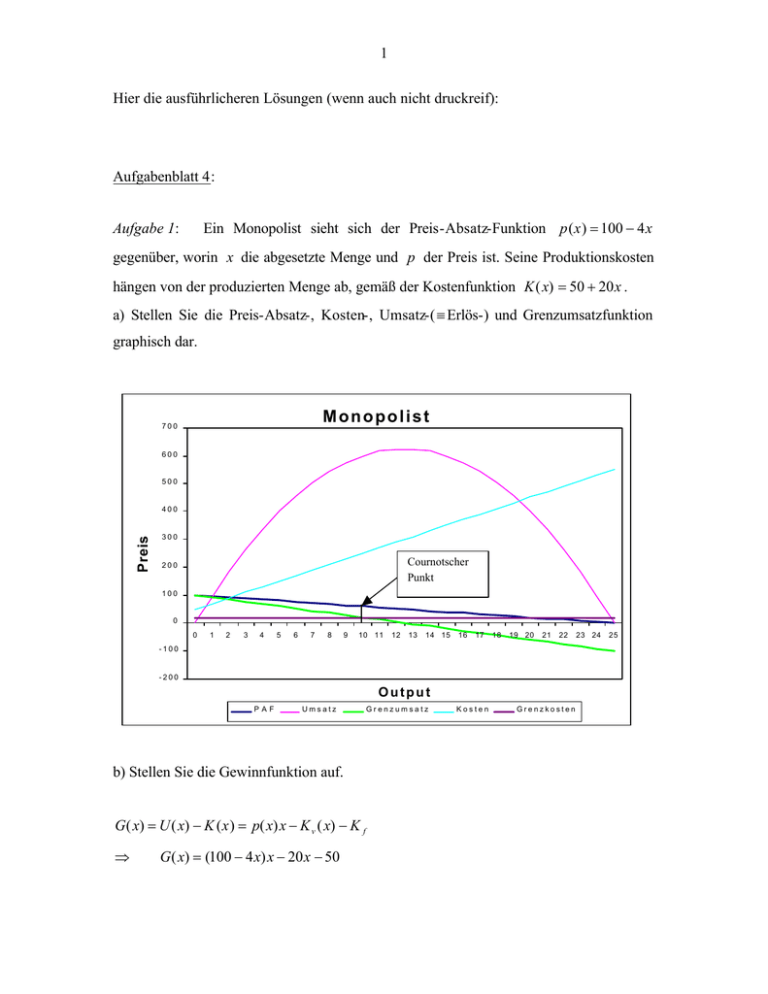
1
Hier die ausführlicheren Lösungen (wenn auch nicht druckreif):
Aufgabenblatt 4:
Ein Monopolist sieht sich der Preis-Absatz-Funktion p ( x ) = 100 − 4 x
Aufgabe 1:
gegenüber, worin x die abgesetzte Menge und p der Preis ist. Seine Produktionskosten
hängen von der produzierten Menge ab, gemäß der Kostenfunktion K ( x) = 50 + 20 x .
a) Stellen Sie die Preis-Absatz-, Kosten-, Umsatz-( ≡ Erlös-) und Grenzumsatzfunktion
graphisch dar.
Monopolist
700
600
500
Preis
400
300
Cournotscher
Punkt
200
100
0
0
1
2
3
4
5
6
7
8
9
10 11
12
13
14 15
16
17
18
19 20
21
22
-100
-200
Output
PAF
Umsatz
b) Stellen Sie die Gewinnfunktion auf.
G( x) = U ( x) − K ( x ) = p( x) x − K v ( x) − K f
⇒
G( x) = (100 − 4 x) x − 20 x − 50
Grenzumsatz
Kosten
Grenzkosten
23 24
25
2
c) Berechnen Sie die gewinnmaximale Absatzmenge (≡ Output, Produktionsmenge) und
den gewinnmaximalen Preis.
max G
x
!
⇒
G′( x ) = U ′( x) − K ′( x) = 0
⇒
G′( x ) = p′( x ) x + p( x) − K ′v ( x ) − K ′f = 0
⇒
G′( x ) = −4 x + (100 − 4 x) − 20 = 0
⇔
80 − 8 x = 0
⇔
x ∗ = 10
⇒
p = 100 − 4 ⋅10 ⇔ p ∗ = 60
!
d) Finden Sie den Cournot-Punkt in der Graphik aus Aufgabenteil a).
Cournot-Punkt
ist
der
Punkt
auf
der
Preis-Absatz-Funktion,
gewinnmaximierenden Menge entspricht (siehe Abb. unter a) ).
e) Berechnen Sie Umsatz, Kosten und Gewinn beim gewinnmaximalen Preis.
Umsatz = Preis × Absatzmenge:
U = p (x )x
⇒ U = 60 ⋅ 10 ⇔ U * = 600
Gesamtkosten = variable Kosten + fixe Kosten:
K = K v ( x) + K f
⇒
K = 20 ⋅ 10 + 50 ⇔ K * = 250
Gewinn = Umsatz − Gesamtkosten:
G = U ( x ) − K ( x)
⇒
G = 600 − 250 ⇔ G* = 350
f) Bei welcher Absatzmenge wird der maximale Umsatz erzielt?
der
der
3
max U ( x)
x
⇒
!
U ′( x) = 0 ⇔
!
p ′( x) x + p ( x ) = 0 ⇒
− 4 x + (100 − 4 x ) = 0 ⇔
xUmsatz∗ = 12.5
g) Zeigen Sie allgemein (und erläutern Sie inhaltlich): im Monopol ist der Grenzumsatz
kleiner als der Absatzpreis, sofern die Preis-Absatz-Funktion fallend verläuft.
U ′( x) = p ′( x) x + p( x) < p ( x ) ⇔
p ′( x ) x < 0 , d.h. bei negativ geneigter Preis-Absatz-
Funktion.
Die Nachfragefunktion nach einem Gut sei x ( p ) = 120 − p . Der einzige
Aufgabe 2:
Anbieter in diesem Markt hat die Kostenfunktion K ( x) = 10 + 5 x 2 .
a) Wie hoch ist der prozentuale Abstand m zwischen Preis und Grenzkosten im
Gewinnmaximum?
x ( p ) = 120 − p ⇔ p ( x ) = 120 − x
G( x) = U ( x) − K ( x ) = p( x) x − K v ( x) − K f
⇒
G( x) = (120 − x ) x − 5 x 2 − 10
max G
x
!
⇒
G′( x ) = U ′( x) − K ′( x) = 0
⇒
G′( x ) = p′( x ) x + p( x) − K v′ ( x) − K ′f = 0
⇒
G′( x ) = − x + (120 − x ) − 10 x = 0
⇒
x ∗ = 10
⇒
p = 120 − 10
!
⇔
p * = 110
4
K ′v ( x * = 10) = 10 ⋅ 10 = 100
m=
110 − 100 1
p − K′
=
⇒ m* =
110
11
p
b) Ist es notwendig immer der Fall, daß der gewinnmaximale Monopolpreis über den
Grenzkosten liegt?
!
Im Gewinnmaximum gilt: p ′( x) x + p( x ) = K ′( x) . Bei fallender Preis-Absatz-Funktion
[ p ′( x ) < 0 ] gilt damit: p ( x ) > K ′( x) .
c) Zeigen Sie: Wenn sich die Preiselastizität der Nachfrage (im Absolutbetrag) erhöht,
sinkt der prozentuale Preis-Grenzkosten-Abstand (Marge). Erläuterns Sie dieses Ergebnis
inhaltlich.
Preiselastizität der Nachfrage: ε p , x
∂x
= x >0
∂p
p
Preis-Grenzkosten-Abstand (≡ Marge):
Gewinnmaximierung
⇒ U ′( x) = K ′( x)
⇒ p+
dp
x = K ′( x)
dx
dp
x
dx
⇔
p − K ′( x) = −
⇔
p − K ′( x )
dp x
=−
p
dx p
5
p − K ′( x )
1
1
=−
=−
dx p
p
ε
dp x
⇔
m=
p − K′
1
1
=− ⇒ m =
⇒
p
ε
ε
dm
1
=− 2 <0
dε
ε
Je höher die Preiselastizität der Nachfrage, desto höher die Ausweichmöglichkeit der
Konsumenten, desto geringer die Möglichkeit des Monopolisten hohe Preise
durchzusetzen.
Im Grenzfall ε → ∞ gilt p = K ′ , was dem Fall dem Fall der vollkommenen Konkurrenz
entspricht,
wo
Unternehmen
sich
einer
konstanten
Preis-Absatz-Funktion
gegenüberstehen.
Aufgabe 3:
(Klausuraufgabe WS 98/99) Ein Monopolist hat eine lineare Preis-Absatz-
Funktion und konstante Grenzkosten in Höhe von g = 4 . Beim gewinnmaximalen Preis
p * beträgt seine prozentuale Preis-Grenzkosten-Marge [ m = ( p * − g ) / p * ] zwanzig
Prozent. Bei welchem Preis würde sein Absatz auf null sinken?
(1) p ( x ) = a − bx
(2) m =
p* − g
= 0.2
p*
K ′(x ) = 4
Wenn der Absatz x auf Null sinkt, gilt der Prohibitivpreis p = a .
Gewinn:
G( x) = U ( x) − K ( x )
6
Gewinnmaximierung:
max G ( x )
x
!
⇒
G′( x ) = U ′( x) − K ′( x) = 0
⇒
G′( x ) = p′( x ) x + p( x) − K ′v ( x) − K ′f = 0
⇒
G′( x ) = −bx + ( a − bx) − g = 0
(3) ⇔
!
x* =
a− g
2b
(3) in (1) einsetzen:
a−g
⇒ p( x ) = a − b 

 2b 
(4) ⇔ p( x ) =
2a a g a + g
− + =
2 2 2
2
(4) in (2) einsetzen:
a+ g
g
⇒ m= 2 −
= 0. 2
a+ g a+ g
2
2
⇔ 1 − 0. 2 =
2g
a+g
⇔ 0.4( a + g ) = g
⇔ 0. 4a = 0.6 g
⇔ a = 1. 5 g
g =4
⇒ a = 1. 5 ⋅ 4 = 6
⇒ p = a =6
7
Aufgabe 4:
Ein Monopolist hat eine linear fallende Preis-Absatz-Funktion und eine
lineare Kostenfunktion mit Fixkosten und konstanten Grenzkosten.
a) Zeigen Sie: bei den unterstellten Nachfrage- und Kostenfunktionen ist der
Monopolpreis der Durchschnitt aus Prohibitivpreis und Grenzkosten.
Lineare Preis-Absatz-Funktion: p ( x ) = a − bx
Prohibitivpreis: Preis bei dem Absatz x auf Null sinkt: p Prohibitiv = a .
Gewinn:
G( x) = U ( x) − K ( x )
Gewinnmaximierung:
max G ( x )
x
!
⇒
G′( x ) = U ′( x) − K ′( x) = 0
⇒
G′( x ) = p′( x ) x + p( x) − K ′v ( x) − K ′f = 0
⇒
G′( x ) = −bx + ( a − bx) − g = 0
⇒
a − 2bx − g = 0
⇒
x *M =
⇒
p *M = a − bx*M ⇒
!
⇔ p *M =
a−g
2b
a− g
a − g 2a − (a − g )
p *M = a − b 
=
=a−
2
2
 2b 
a+ g
2
b) Zeigen Sie: bei den unterstellten linearen Nachfrage- und Kostenfunktionen wird eine
Grenzkostenerhöhung genau zur Hälfte im Preis überwälzt.
8
dp*M 1
=
dg
2
Aufgabe 5:
In einem Markt mit monopolistischer Konkurrenz seien für alle Anbieter
die Grenzkosten g = 2 . Die Preis-Absatz-Funktion des einzelnen Anbieters i sei
pi = p + 1000 / n − xi , wobei p der Durchschnittspreis im Markt ist und n die Zahl der
Anbieter.
a) Berechnen Sie den gleichgewichtigen Durchschnittspreis in diesem Markt als Funktion
von n , der Zahl der Anbieter im Markt.
(1) p i = p +
1000
− xi , i = 1...n
n
gi = g = 2
[ (1) ergibt sich aus pi = p + hi − bi xi , wobei bi = 1 und hi = h =
h1 + h2 + ... + hn
, also
n
Symmetrie im Produktdifferenzierungsvorteil bei den Anbietern angenommen wird.]
Gesucht: gleichgewichtiger Durchschnittspreis pˆ ( n)
Gewinn:
Gi ( x ) = U i ( x) − K i ( x )
Gewinnmaximierung:
max Gi ( x i )
xi
!
⇒
G i′ ( x ) = U i′ ( x ) − K i′ ( x ) = 0
⇒
G′i ( x i ) = p ′i ( xi ) xi + pi ( xi ) − K v′ ( xi ) − K ′f = 0
!
9
− xi +  p +

⇒
(2) ⇔ x *i =
1000
− xi  − g = 0
n

p 500 g
+
−
2
n
2
(2) in (1) einsetzen:
⇒ p *i = p +
⇔ p *i =
pˆ =
1000  p 500 g 
− +
− 
n
n
2
2
p 500 g
+
+ (gilt aufgrund von Symmetrie für alle Anbieter)
2
n
2
p1* + p*2 + ... + pn* 1
p 500 g
 p 500 g 
= ∑ pi* = n +
+  n= +
+
n
n i
n
2
2
n
2
2
Im Gleichgewicht gilt pˆ = p :
⇒ p=
⇔
p 500 g
+
+
2
n
2
p 500 g
=
+
2
n
2
⇔ p=
1000
+g
n
(3) ⇒ pˆ = p =
g =2
1000
+2
n
b) Berechnen Sie die Ausbringungsmenge
xi
des
Marktgleichgewicht als Funktion der Zahl der Anbieter n .
einzelnen
Anbieters
im
10
Aus (2)
x *i =
p 500 g
+
−
2
n
2
(3) in (2) einsetzen:
⇒
⇔
 1000 

+2
n 
500 g

*
xi =
+
−
2
n
2
x *i =
Aufgabe 6:
g =2
1000
n
In
einem
Markt
mit
monopolistischer
Konkurrenz
seien
die
Kostenfunktionen und Preis-Absatz-Funktionen der n Anbieter wie folgt gegeben:
K i = xi + 16 und p i = p +
500
− xi . Hierin ist p der Durchschnittspreis im Markt.
n
a) Die Anbieterzahl sei n = 100 . Berechnen Sie das gleichgewichtige Preisniveau und die
Gewinne für die gegebenen Anbieterzahl. Wie hoch ist der durchschnittliche
Produktdifferenzierungsvorteil? Wie hoch sind die durchschnittliche Fixkosten pro
Stück?
(1) p i = p +
500
− xi
n
(2) K i = xi + 16
Gewinn:
Gi ( x ) = U i ( x) − K i ( x )
Gewinnmaximum:
11
max Gi ( x i )
xi
!
⇒
G i′ ( x ) = U i′ ( x ) − K i′ ( x ) = 0
⇒
G′i ( x i ) = p ′i ( xi ) xi + pi ( xi ) − K v′ ( xi ) − K ′f = 0
⇒
− xi + p +
!
500
− xi − 1 = 0
n
p 250 1
+
−
2
n
2
(3) ⇔ x *i =
(3) in (1) eisetzen:
⇒ p *i = p +
⇔ p *i =
pˆ =
500  p 250 1 
− +
− 
n
n
2
2
p 250 1
+
+
2
n
2
1
p 250 1 
p 250 1
pi* = n +
+  n= +
+
∑
n i
n
2
2
n
2
2
Im Gleichgewicht gilt pˆ = p :
⇒ p=
⇔
⇔
p 250 1
+
+
2
n
2
p 250 1
=
+
2
n
2
p=
500
+ 1 n = 100
n
500
+1 = 6
⇒ p = ˆp =
100
⇒
xi* =
p 250 1
+
−
2
n
2
p=
500
+1
n
12
⇒
x i* =
500 1 250 1
+ +
−
2n 2
n
2
⇒
x i* =
500
n
⇒
x *i = 5
n = 100
Berechnung Gewinn Gi für n = 100 .
Gewinn:
Gi ( xi ) = U i ( xi ) − Ki ( xi )
⇒
Gi ( xi ) = pi ( xi ) xi − K i ( xi )
⇒
500

Gi ( x i ) =  p +
− xi  xi − x i − f i
n


⇔
500 
Gi ( x i ) = 
 − fi
 n 
⇒
500 
G ( x ) = 
 − 16 = 25 − 16 = 9
 100 
p=
500
500
+ 1, x *i =
n
n
2
n = 100, f i = 16
2
*
i
*
i
Gesucht: durchschnittliche Produktdifferenzierung h
pˆ =
p h g
+ +
2 2 2
im GG gilt p = pˆ
⇒
p=
p h g
+ +
2 2 2
13
⇔
h p− g
=
2
2
⇔
h = p−g
⇒
h =5
p = 6, g = 1
Gesucht: durchschnittliche Fixkosten per Stück:
Dafür werden die durchschnittlich optimalen Ausbringungsmengen x benötigt.
x =
1 n *
∑ xi
n i =1
x=
nxi*
= xi* = 5 .
n
f =
1 n
∑ fi , wobei wiederum aufgrund der Symmetrie der Anbieter gilt
n i =1
f =
nf i
= f i = 16
n
bzw.
aufgrund
der
Symmetrie
der
Anbieter
gilt
einfacher
Die durchschnittlichen Fixkosten per Stück sind dann
f 16
=
= 3.2
x 5
b) Berechnen Sie die gleichgewichtige Anbieterzahl bei freiem Markteintritt. Wie hoch
sind im langfristigen Gleichgewicht die unter a) berechneten Größen?
Die auf die Produkteinheit umgelegte Fixkostenbelastung k ergibt sic h im Markt als die
Summe der Fixkosten geteilt durch A , also
14
k =
nf
,
A
wobei A = x1 + x 2 + ... + xn und aufgrund der Symmetrie der Anbieter A = nxi .
⇒ k =
nf
nf
nf
=
=
500  500
nxi
n

 n 
xi =
500
n
Die durchschnittliche Marge m = p − g (Preis minus Grenzkosten) muß die Fixkosten
pro Stück finanzieren. Sie ist im Gleichgewicht
m = p− g = h
⇒ m=
g = 1, p =
500
+1
n
500
500
+ 1−1 =
1
n
im GG gilt m = k
⇒
500 nf
=
n
500
⇔ n 2 f = 500 2
⇔ n* =
500
⇒ n* =
500
= 125
4
p=
f = 16
f
500
+1
n*
⇒
p=
500
+1 = 5
125
15
x i* =
x=
500
n*
⇒
x *i = 4
n * x*i
= xi* ⇒ x = 4
*
n
2
500
G ( x ) =  *  − 16
 n 
*
i
*
i
⇒ G i* ( x i* ) = 16 − 16 = 0
h = p − g ⇒ h = 5−1= 4
f 16
=
=4
x 4
c) Die Fixkosten steigen auf 25. Wieviel Unternehmen verbleiben langfristig im Markt?
Zu welchen Preisen bieten sie welche Mengen an? Wie hoch sind im neuen langfristigen
Gleichgewicht die durchschnittlichen Fixkosten pro Stück?
f i = 25 , aufgrund Symmetrie der Anbieter gilt dann
f = 25
im GG gilt m = k
⇒
500 nf
=
n
500
⇔ n 2 f = 500 2
⇔ n* =
500
f
f = 25
16
⇒ n* =
p=
500
+1
n*
x i* =
x=
500
= 100
5
500
n*
500
+1 = 6
100
⇒
p=
⇒
x *i = 5
n * x*i
= xi* ⇒ x = 5
n*
2
500
G i* ( x i* ) =  *  − 25
 n 
⇒ G i* ( x i* ) = 25 − 25 = 0
h = p − g ⇒ h = 6 −1 = 5
f 25
=
=5
x
5
Aufgabe 7:
Die Preis-Absatz-Funktion in einem homogenen Markt sei p = a − bx . Es
gibt zwei Anbieter in diesem Markt. Die Kostenfunktion des Anbieters 1 lautet
K1 = F1 + c1 x1 , die des Anbieters 2 lautet K 2 = F2 + c 2 x 2 , worin die F Fixkosten
darstellen. Es gilt x = x1 + x 2 .
a) Stellen Sie die Gewinnfunktion der beiden Anbieter auf.
Gewinnfunktion Anbieter 1:
17
G1 ( x1 , x 2 ) = U1 ( x1 , x 2 ) − K1 ( x1 )
⇒
G 1 ( x 1 , x 2 ) = p ( x 1 , x1 ) x 1 − K 1 ( x1 )
⇒
G1 ( x1 , x 2 ) = [ a − b( x1 + x 2 )] x1 − (c1 x1 + F1 )
ähnlich für Anbieter 2:
G2 ( x 2 , x1 ) = [ a − b( x1 + x 2 )] x1 − (c 2 x2 + F2 )
b) Finden Sie die Reaktionskurven und stellen Sie sie graphisch dar. Welche Annahme
über das strategische Verhalten müssen Sie bei der Ableitung treffen?
max G1 ( x1 , x2 )
x1
!
⇒
G1′ ( x1 , x 2 ) = U1′ ( x1 , x2 ) − K1′ ( x1 ) = 0
⇒
G1′ ( x1 , x 2 ) = p ′( x1 , x 2 ) x1 + p( x1 , x 2 ) − K1′( x1 ) = 0
⇒
G1′ ( x1 , x 2 ) = −bx1 + [a − b ( x1 + x 2 )] − c1 = 0
⇒
2bx1 = a − bx 2 − c1
⇒
x1* =
!
a − bx 2 − c1
Reaktionskurve von Anbieter 1
2b
ähnlich für Anbieter 2:
⇒
x *2 =
a − bx1 − c2
Reaktionskurve von Anbieter 2
2b
(graphische Darstellung siehe Übung)
Cournot Annahmen:
-
Mengenwettbewerb
-
Homogene Güter
18
-
Angebotsmengen werden von beide Anbietern gleichzeitig unabhängig voneinander
bestimmt
-
Optimierung der eigenen Angebotsmenge gegeben der Angebotsmenge des
Konkurrenten → im Cournot-Nash-Gleichgewicht ist Abweichen von der eigenen
Angebotsmenge dann nicht mehr lukrativ.
c) Finden Sie die gleichgewichtigen Mengen der beiden Anbieter und den
gleichgewichtigen Marktpreis.
Einsetzen der Reaktionskurve von Anbieter 2 in die von Anbieter 1, bzw. vice versa.
 a − bx1 − c 2 
a − b
 − c1
2b


⇒ x1 =
2b
⇔ 2bx1 = a −
⇔ 2bx1 −
⇔
a bx1 c2
+
+ − c1
2 2
2
bx1 a − 2c1 + c2
=
2
2
a − 2c1 + c 2
3
bx1 =
2
2
⇔ x1* =
a − 2c1 + c 2
3b
ähnlich für Anbieter 2:
x *2 =
a − 2c 2 + c1
3b
x * = x1* + x *2 =
⇔ x* =
a − 2c1 + c 2 a − 2c 2 + c1
+
3b
3b
2a − c1 − c 2
3b
19
p * = a − bx *
 2 a − c1 − c 2 
⇒ p * = a − b

3b


⇔ p* =
3a − 2a + c1 + c2 a + c1 + c 2
=
3
3
d) Zeigen Sie: Eine Erhöhung der Grenzkosten des Anbieters 1 wird seinen Marktanteil
verringern.
a − 2 c1 + c 2
x1
a − 2c1 + c 2
3b
=
=
Marktanteil von Anbieter 1: s1 =
x1 + x 2 2a − c1 − c 2 2 a − c1 − c 2
3b
ds1 − 2( 2a − c1 − c 2 ) − [ −( a − 2c1 + c 2 )] − 4 a + 2c1 + 2c2 + a − 2c1 + c 2
3(c 2 − a)
=
=
=
2
2
dc1
( 2a − c1 − c 2 )
( 2a − c1 − c2 )
( 2a − c1 − c 2 ) 2
Da ( 2a − c1 − c 2 ) 2 > 0 , gilt
ds1
< 0 wenn c 2 < a , was gegeben ist, da sonst Anbieter 2
dc1
nicht auf dem Markt produzieren würde.
Aufgabe 8:
a) Ein Unternehmen auf einem homogenen Konkurrenzmarkt hat die Kostenfunktion
K ( x) = x 3 − 18 x 2 + 120 x + 300 . Berechnen Sie die Angebotsfunktion.
Gewinn:
Gi ( x ) = U i ( x) − K i ( x )
⇔ Gi ( x ) = px1 − Ki ( x )
Gewinnmaximum:
20
max Gi ( x i )
xi
!
⇒
Gi′( xi ) = Ui′( xi ) − K i′( xi ) = 0
⇒
G′i ( x i ) = p − K v′ ( xi ) − K ′f = 0
⇒
p = K ′( xi )
⇒
p = 3 x 2 − 36 x + 120
⇒
3x 2 − 36 x = p − 120
⇒
x 2 − 12 x =
⇒
x 2 − 12 x + 36 =
⇒
( x − 6) 2 =
⇒
x −6 =
⇒
x=
!
p
− 40
3
p
−4
3
p
−4
3
p
−4
3
p
− 4 + 6 , für p ≥ 12
3
b) Wieviel wird ein vollständig kompetitives Unternehmen mit der Kostenfunktion
K = 25 x + 12 anbieten, wenn der Marktpreis p = 30 beträgt?
p = K ′( xi ) ⇒ p = 25
Produziert soviel wie technisch möglich fall p ≥ 25 (also auch bei p = 30 ) und nichts
falls p < 25 .
Aufgabe 9:
Die Angebotsfunktion auf einem Markt mit vollständiger Konkurrenz ist
x A = 100( p − 1) für p > 1 ; die Nachfragefunktion ist x N = 500 − 200 p .
a) Berechnen Sie den gleichgewichtigen Marktpreis.
21
Im Gleichgewicht gilt
xA = xN
⇒
100( p − 1) = 500 − 200 p
⇔
100 p − 100 = 500 − 200 p
⇔
p* = 2
⇒
x * = 100(2 − 1) = 100
b) Der Staat erhebt pro verkaufter Einheit des Gutes eine Steuer von 1 Euro von den
Anbietern. Wieviel Prozent dieser Stücksteuer wird auf die Nachfrager überwälzt?
p (x A ) = 1 +
xA
100
5 xN
−
2 200
p (x N ) =
p ( x A , Steuern ) = p ( x A ) + 1 = 2 +
xA
100
Im Gleichgewicht gilt:
p ( x A , Steuern ) = p ( x N )
⇒ 2+
x
5
x
= −
100 2 200
⇔
3x 1
100
= ⇔ x *, Steuern =
200 2
3
⇒
p *, Steuern = 2 +
1
3
1

2 +  − 2
−p
3
=
t
1
*,Steuern
*
⇒
p
⇔
p *,Steuern − p * 1
=
t
3
wobei t (Steuern) = 1
Ein Drittel bzw. 33,33% der Steuer werden auf die Nachfrager überwälzt.