Wettbewerb-/Absatzmodelle

Wettbewerb-/Absatzmodelle
Was bisher geschah:
I
Modellierung der Kostenfunktion für ein beliebiges Gut
I
Modellierung der Nachfrage nach Gütern um die
Nachfragekurve darzustellen
Wie es weitergeht:
I
ausgehend von der Produktions- und der hergeleiteten
Kostenfunktion kann man einen Schritt weiter gehen: wie groß
ist das Marktangebot bei einem bestimmten Preis?
1 / 88
Profitmaximierung
Ausgangspunkt: Vorstellung von Firmen, möglichst großen Gewinn
machen. Gewinn definiert als Erlöse (revenues, R) minus Kosten
(costs, C).
max Π = R(q) − C (q).
q
Suche nach Extremstelle mittels erster Ableitung:
dR(q) dC (q)
dΠ(q)
=
−
dq
dq
dq
Erster Summand wird Grenzerlös genannt (marginal revenue, MR),
zweiter Grenzkosten (marginal cost, MC ). Ebenso muss gelten
Bedingung zweiter Ordnung:
d 2 Π(q)
d 2 R(q) d 2 C (q)
=
−
< 0.
dq 2
dq 2
dq 2
2 / 88
Profitmaximierung
Null setzen der ersten Ableitung:
dΠ(q)
dR(q)
dC (q)
=0⇒
=
dq
dq
dq
beide Ausdrücke haben die äquivalente und sinnvolle ökonomische
Bedeutung:
I
die letzte produzierte Einheit bringt keinen zusätzlichen
Gewinn mehr, verringert ihn aber auch nicht
I
die letzte produzierte Einheit kostet genau so viel zusätzlich
(MC (q)), wie sie an zusätzlichen Erlösen einbringt (MR(q))
sonst: Erhöhen des Outputs erhöht den Gewinn (bei MR > MC
bzw. dΠ/dq > 0), oder umgekehrt;
3 / 88
Wettbewerbsmodelle
Grundlegende Wettbewerbsmodelle:
I
Monopol: es gibt nur eine Firma, die einen Markt bedient
I
Vollkommene Konkurrenz: entgegengesetzter Extremfall des
Monopols; es gibt sehr viele Firmen, sodass eine einzelne gar
keinen Einfluß auf den Markt hat
I
Oligopol: einige wenige Firmen teilen sich den Markt
4 / 88
Vollkommene Konkurrenz
Vollkommener Wettbewerb: grundlegendes Modell des Marktes;
Annahmen sind:
I
viele Käufer und viele Verkäufer (sodass beide keinen“
”
Einfluß auf den Marktpreis p haben)
I
homogene (identische) Produkte
I
vollkommene Information über Preise und Homogenität der
Produkte
I
keine Transaktionskosten
I
Markteintritt und -austritt ist jederzeit möglich
Daher: Produzenten kalkulieren unter der Annahme eines fixen
Marktpreises p. Sinnvoll z.B. für Agrarmärkte.
5 / 88
Angebot bei Vollkommenem Wettbewerb
Firmen sind Preisnehmer. Drückt sich im Modell aus durch:
R(q) = p · q,
Preis hängt nicht von Produktionshöhe q ab, sondern wird im
Max-problem der individuellen Firma konst. betrachtet.
Für die Profitmaximierungsüberlegung gilt wegen MR(q) = p und
MR(q) = MC (q) im Optimum:
p = MC (q)
Beachte: p = MC (q) ist daher eine individuelle (inverse)
Angebotsfunktion. Die individuell Angebotsfunktion für diese
Firma i ist q = Si (p). Einschränkung: Preis muss mindestens die
Durchschnittskosten decken.
6 / 88
Graphische Darstellung
7 / 88
Wettbewerb Kurzfristig vs. Langfristig
Vorangehendes Beispiel betrifft den langfristigen Fall: die
Inputfaktoren können optimal eingesetzt werden und es gibt keine
Fixkosten.
Bemerkung: Fixkostenkomponente bei positiver Produktion nicht
ausgeschlossen, sog. quasi-fixe Kosten
fixe Kosten (kurzfristig):
C (q) = F + VC (q) für q ≥ 0
quasi-fixe Kosten (FQ möglich):
0
für q = 0
C (q) =
FQ + VCQ (q) für q > 0
8 / 88
Wettbewerb Kurzfristig vs. Langfristig
Also, langfristig, keine Fixkosten, produziere bei p = MC (q) unter
der Bedingung Π(q) ≥ 0 ⇔ p ≥ AC (q)
Kurzfristig kann es Fixkosten geben, und es kann auch sinnvoll
sein, bei Verlusten zu produzieren. Wann? Wenn die Verluste bei
Produktionsstopp (C (q = 0) = F , Fixkosten) vermindert werden
können durch positive Produktion. Das ist der Fall wenn
p > AVC (q). Der Preis muss also kurzfristig mindestens die
variablen Durchschnittskosten decken.
9 / 88
Angebotsfunktion und Zshg. mit Fixkosten Graphisch
p > min VAC (q)
:
p > min AC (q) :
Verlust beginnt zu sinken; F wird abbezahlt.
Gewinne beginnen.
10 / 88
Kurzfristiges Marktangebot
Beachte: Produktionsentscheidung festgelegt ( Kapitalstock
”
fixiert“), Anzahl der Firmen fixiert; seien alle Firmen identisch:
SGES = S1 (p) + S2 (p) + . . . + SN (p) =
N
X
Si (p) = N · Si (p).
i=1
11 / 88
Wettbewerb in der langen Frist
Kurzfristig: Outputerhöhungen führen zu Bewegung entlang der
Angebotskurve der N Firmen im Markt
Langfristig: unter der Vorstellung des Preiswettbewerbs; solange
p > min(AC (q)) kann eine neue Firma mit q = arg min AC (q)
eintreten und zu p = (Markpreis - ε) anbieten → Gewinn
daher, Eintrittsdynamik führt zu folgenden Resultaten:
I
Produktion bei p = min(AC ) beliebig groß, vollkommen
”
elastisch“, Angebotskurve ist langfristig horizontal
I
Eintritt wenn Π > 0 und Marktaustritt wenn Π < 0; im
langfristigen Gleichgewicht Πi = 0
I
effiziente Produktion: wenn Firmen identische Kosten haben,
kann sich uneffizient produzierende Firma bei Π = 0 nicht
behaupten
12 / 88
Long Run Supply
LR-Supply-Kurve ist gleich LRMC ≥ min(LRAC)
Abweichen von p > min(AC ) durch Unterbieten des Marktpreises p
ist langfristig immer gewinnbringend für einen Neu-Eintretenden
13 / 88
Andere Formen von Angebotskurven
Beschränkte Anzahl von Firmen: Angebot setzt sich zusammen wie
im SR und höhere Nachfrage bedeutet höheren Preis.
Steigende Inputpreise: Kostenkurven verschieben sich ab gewisser
Nachfrage nach oben → Marktpreis steigt mit steigender
Nachfrage.
Unterschiedliche Kostenfunktionen von Firmen, z.B.: Zu niedrigem
Preis können nur Niedrigkostenfirmen (/-länder) produzieren, bei
höherem Marktpreis kommen Firmen hinzu → Angebot steigt bei
steigendem Marktpreis/ Preis steigt bei steigender Nachfrage.
14 / 88
Long-Run Angebot für Baumwolle
Produktionskosten unterschiedlich wegen Unterschieden in
Bodenqualität, Regen, Bewässerungskosten, Arbeitskosten, etc.
Anmerkung: Grenzkosten pro Land als konstant angenommen.
15 / 88
Bsp.: Angebotsfunktion
Kurzfristige Kostenfunktion einer Firma:
Cs (q) = 4 + 2q + q 2 .
Was ist die kurzfristige Angebotsfunktion, ss (p), dieser Firma im
vollkommenen Wettbewerb?
Langfristige Kostenfunktion einer Firma sei:
C` (q) = 4 + q 2 .
Wie sieht die langfristige Angebotsfunktion, s` (p), dieser Firma
aus? Wie sieht die Marktangebotsfunktion S` (p) aus?
16 / 88
Ursache für Monopole
Grundidee: einzelner Wettbewerber kann ohne Beschränkungen
Gewinn maximieren
I
Monopolist ist einziger Anbieter in einem Markt
I
daher ist sein Output q = Marktoutput X
I
Marktnachfrage = Nachfrage für Monopolist
I
Monopolist sei Preissetzer
I
Ziel: wie immer, Profitmaximierung
Grund: Eintrittsbarrieren, z.B.
I
administrativ/gesetzlich: Telekommunikationsmarkt, Post,
Schienengüter/-personenverkehr, Luftverkehr, Energiemarkt;
Anm: Deregulierungspolitik
I
strukturell: nicht wettbewerbsfähige Kostenstrukturen
17 / 88
Nachfragefunktion
Nachfragefunktion X (p) ist die Essenz aus der Haushaltstheorie;
beschreibt wie groß die nachgefragte Menge X ist, gegeben den
Preis p
I
X (p = 0): Sättigungsmenge
I
X (p) = 0: p ist der Prohibitivpreis
I dX :
dp
Mengeneinheiten, um die sich Nachfrage erhöht wenn sich
p um eine Einheit erhöht
Anstatt der Ableitung der Nachfrage ist manchmal die
mengeneinheitenunabhängige Preiselastizität informativer:
∆X
X ∆p→0
→
∆p
p
dX p
= X ,p
dp X
Interpretation: gibt die Prozent der Veränderung der Menge an,
pro Prozent Veränderung des Preises
18 / 88
Lineare Nachfragefunktion
X (p) = d − ep
I
Sättigungsmenge: X (p = 0) = d
Prohibitivpreis: X (p) = 0 = d − ep ⇔ p =
dX
dp = −e
I
X ,p =
I
I
dX p
dp X
d
e
p
= −e d−ep
19 / 88
Gewinn
Gewinn per Definition gleich Erlös (revenue) minus Kosten (cost)
Π=R −C
Wie läßt sich der Gewinn als Funktion des Preises darstellen,
Π(p) =? Erlös ist Preis mal Menge, Menge hängt vom Preis ab:
R(p) = p · X (p)
Kosten hängen von Produktionshöhe X ab, aber diese wiederum
vom Preis:
C (X ) = C X (p)
Zusammengefasst:
Π(p) = pX (p) − C X (p)
20 / 88
Gewinnmaximierung
Ziel:
FOC:
max Π(p)
p
dΠ(p)
=0
dp
Erste Ableitung:
dΠ(p)
dR(p) dC X (p)
=
−
dp
dp
dp
Interpretation der FOC: sowohl eine Preiserhöhung als auch eine
-senkung führen zu keiner Gewinnveränderung; Gewinn kann durch
Preisveränderung nicht mehr gesteigert werden (gegeben SOC
erfüllt)
21 / 88
Grenzerlös bezüglich des Preises
d
dR(p)
=
p · X (p)
dp
dp
dX
= X (p) + p
dp
Interpretation:
I
Erster Summand: für jede Mengeneinheit, die bei p
nachgefragt wird, bekommt man eine (kleine) Geldeinheit
mehr, wenn p um eine kleine Geldeinheit steigt
I
Zweiter Summand: die Nachfrage sinkt wenn p steigt, und für
jede Einheit X , die bei einer Erhöhung von p verloren geht,
geht deren Preis (=Erlös pro Einheit) verloren
22 / 88
Monopol vs. Wettbewerb
Neu im Monopolmodell: Überlegung, dass ein einzelner Anbieter
Nachfrage nicht vollkommen elastisch sieht (wie bei Wettbewerb),
beeinflusst Umsatzkalkül:
Wettbewerb
Monopol
R1 = A, R2 = A + B,
∆R = B = p1
R1 = A + C , R2 = A + B,
∆R = B − C = p2 − C < p1
23 / 88
Grenzerlös und Elastizität
Grenzerlös kann als Funktion der Elastizität dargestellt werden:
dX
dR(p)
= X (p) + p
dp
dp
dX p = X (p) 1 +
dp X
= X (p) 1 + X ,p
X ,p ist negativ, da Preiserhöhung zu Mengensenkung führt; aber
solange 0 > X ,p > −1 gilt, ist der gesamte Ausdruck positiv; d.h.
solange die Nachfrage unelastisch” ist (so wird sie genannt, wenn
”
die Ungleichung erfüllt ist), führt eine Preiserhöhung zu
Umsatzsteigerung
24 / 88
Darstellung bei Linearer Nachfrage
R(p) = p(d − ep)
dR(p)
= d − ep + p(−e) = d − 2ep
dp
arg maxp R(p) :
d − 2ep = 0 ⇔ p =
d
2e
25 / 88
Grenzkosten bezüglich des Preises
dC X (p)
dC dX
=
·
dp
dX dp
Intrepretation:
I
dC /dX : Grenzkosten bezüglich der Menge; sind positiv, da
(bzw. solange) die Kosten mit der Produktionshöhe steigen
I
dX /dp: Nachfrageveränderung bei Preiserhöhung; negativ
26 / 88
Grenzkosten bei Linearer Kostenfunktion
Lineare Kostenfunktion:
C (X ) = c · X
Da die Menge vom gewählten Preis bestimmt wird:
C X (p) = cX (p)
Bei linearer Nachfragefunktion, X (p) = d − ep:
C X (p) = c(d − ep)
dC
= −ec
dp
Kosten sinken wenn der Preis steigt. Warum? Weil die verkaufte
Menge sinkt, und daher die produzierte Menge, und daher weniger
Kosten anfallen. Hängt von der Steigung der Nachfragefunktion ab.
27 / 88
Darstellung von Erlös und Kosten
I
I
I
I
C (p) = R(p) ⇒ cX (p) = pX (p) ⇔ c = p
R 0 (p) = 0
R 0 (p) = C 0 (p); gleiche Bedingung wie FOC
Π0 (p) = R 0 (p) − C 0 (p) = 0, also p ? = arg maxp Π(p)
R(p) = C (p) = 0 beim Prohibitivpreis, X (p) = 0
28 / 88
Optimum
FOC (Voraussetzung: SOC erfüllt und FOC liefert Maximum):
MR = MC
Interpretation: die Erhöhung des Preises um die letzte (kleine)
Einheit bringt genau so viel (MR) wie sie kostet (MC)
Bei linearer Nachfrage:
d − 2ep = −ec ⇔ p =
d + ec
2e
29 / 88
Optimum
fortgesetzt
p=
d + ec
2e
Gewinn:
Π(p) = (p − c) X (p)
d + ec
d + ec
−c
d −e
Π(p) =
2e
2e
d + ec − 2ec
d + ec
=
d−
2e
2
d − ec 2d − d − ec
=
·
2e
2
d − ec d − ec
=
·
2e
2
(d − ec)2
=
4e
30 / 88
Monopolist ist Mengensetzer
Monopolist wählt Menge anstatt Preis
Profit: Erlös minus Kosten, aber jetzt in Abhängigkeit der Menge;
Π(X ) = R(X ) − C (X )
C (X ) ist die übliche Form der Kostenfunktion; R = p · X , der Preis
muss jetzt in Abhängigkeit der Menge ausgedrückt werden; diese
Darstellung nennt man inverse Nachfragefunktion, p wird als der
Gleichgewichtspreis beim Angebot X gesehen; also
Π(X ) = p(X ) · X − C (X )
31 / 88
Monopollösung
FOC durch Null setzen des Grenzprofits:
!
Π0 (X ) = MR(X ) − MC (X ) = 0 ⇒ MR(X ) = MC (X )
I
I
optimale Menge bei Schnittpunkt von MR und MC
optimaler Preis auf der Nachfragekurve, zugehörig zur
optimalen Menge
Welche Fläche repräsentiert den Gewinn? Ohne Fixkosten: ABME,
oder ABD
32 / 88
Lösung bei Linearer Nachfrage und Konstanten
Grenzkosten
inv. Nachfragefkt.:
Kostenfkt.:
p(X ) = a − bX
C (X ) = cX
Π(X ) = (a − bX )X − cX
FOC
dΠ/dX = (a − bX ) + (−b)X − c ⇒
0 = a − 2bXM − c
a−c
XM =
2b
33 / 88
Beispiel
Kostenfunktion C (Q) und inverse Nachfragefkt. p(Q):
C (Q) = 12 + Q 2
p = 24 − Q
Lösung
MC
AVC
AC
Π
Π
dΠ
dQ
=
=
=
=
=
2Q,
Q,
Q + 12/Q
p(Q)Q − C (Q)
(24 − Q)Q − Q 2 − 12
!
= 24 − Q − Q −( 2Q ) = 0
|
{z
} |{z}
MR
24 − 2Q = 2Q → Q = 6,
MC
p = 18
p > AVC → Variable Kosten gedeckt p > AC → Π > 0
34 / 88
Graphisch
35 / 88
Beispiele für Modifikationen
Erfahrungskurveneffekte: Effekt auf der Kostenseite;
Produktionshöhe in erster Periode senkt die Kosten für Produktion
in nächster Periode zunehmend; z.B. geringere Fehlerquoten,
geringere Produktionszeiten;
Nachfrageunsicherheit: wenn mit der Preissetzung Informationen
über die Nachfragefunktion erhoben werden sollen, dann muß Preis
auch vom (unbekannten) Monopolpreis abweichen
36 / 88
Monopol und Effizienz
Ineffizienz: wenn es keine Bedrohung des Monopolgewinns etwa
durch potenziellen Markteintritt gibt, dann könnte die Motivation
von Eigentümern, Managern und Arbeitnehmern sinken,
insbesondere wenn unangenehme und einschneidende Maßnahmen
getroffen werden müssten; fehlender Druck, um Prozess- oder
Produktinnovationen durchzuführen kann Gewinn des
Monopolisten über Zeit relativ verringern
Gegenargument: Disziplinierung durch Kapitalmarkt (Gefahr einer
feindlichen Übernahme), oder Möglichkeit der Anreizverbesserung
durch gewinnabhängige Entlohnung
37 / 88
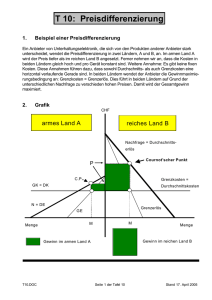
Preisdifferenzierung: Illustration
Anbieter kann einen Markt in zwei Gruppen teilen und
unterschiedliche Preise setzen; Beispiel Kinokarten, für Studenten
(S, Anzahl nS ) billiger als für Berufstätige (B, Anzahl nB );
einfaches Zahlenbeispiel mit Gruppen- und Gesamtprofiten
abhängig von Preisgestaltung (MC sei Null):
pB
5
10
10
5
10
10
pS
5
10
5
5
10
5
nB
10
10
10
10
10
10
nS
20
20
20
5
5
5
ΠB
50
100
100
50
100
100
ΠS
100
0
100
25
0
25
Π
150
100
200
75
100
125
Anmerkung: im ersten Fall steigt der Profit durch durch höheren
Preis für Konsumentengruppe der Berufstätigen, im zweiten Fall
durch die Anziehung einer weiteren Konsumentengruppe, die der
Studenten; 2. Anmerkung: Bsp. für Preisdifferenzierung dritten
”
Grades“
38 / 88
Arten der Preisdiskriminierung
Preisdifferenzierung bedeutet: das gleiche Gut kann zu
verschiedenen Preisen verkauft werden; das war bisher nicht
möglich
I
P. ersten Grades: Perfekte Preisdiskriminierung (2.+ 3. Grad)
I
P. zweiten Grades: unterschiedl. Preise für unterschied.
Mengen
I
P. dritten Grades: unterschiedl. Preise für unterschied.
Gruppen
39 / 88
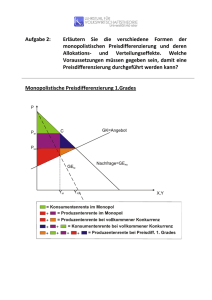
Preisdifferenzierung 1. Grades
Veranschaulichung mittels diskreter Nachfragefunktion:
I
I
I
I
1. Einheit wird zu 6 verkauft, nächste zu 5, übernächste zu 4
Die MR sind der Preis zu jeder Menge, und die MR-Kurve ist
identisch mit der Nachfragekurve
Produktion geht bis Preis gleich Grenzkosten (MC=4 konst.)
Käufer mit hoher Zahlungsbereitschaft haben keinen Vorteil”
”
(Konsumentenrente) mehr davon, dass der einheitliche
Marktpreis unter ihrer Zahlungsbereitschaft liegen würde
40 / 88
Perfekte Preisdiskriminierung
jeder Konsument kann nach Zahlungsbereitschaft unterschieden
werden, und für jeden Konsumenten kann jede Einheit zu einem
unterschiedlichen Preis verkauft werden; ideal für das
Unternehmen: verkaufe jede Einheit eines Gutes jedem Käufer zum
Preis gleich seiner Zahlungsbereitschaft
hypothetische Veranschaulichung: holländische Auktion bei der ein
Gut in Einzelstücken verkauft wird und jeder Käufer jedes Stück
kauft, sobald sein Reservationspreis (holländisch: von oben)
erreicht wird
41 / 88
Preisdifferenzierung 2. Grades
auch: Mengendiskriminierung“
”
Firma weiß, dass für jeden Konsumenten die Zahlungsbereitschaft
mit der Menge sinkt, kann aber unterschiedliche
Zahlungsbereitschaften von unterschiedlichen Konsumenten nicht
feststellen
Beispiel: Elektrizität, Heizöl, Wasser
Preise können für verschiedene Mengen pro Konsument
unterschiedlich sein (Mengenpakete) aber das gilt für alle
Konsumenten gleich
Bsp.: Menge = 0 bis Menge1 kostet p1 , Menge1 bis Menge2 kostet
p2 , etc.
42 / 88
Illustration Mengendiskriminierung
Z.B., konstante Grenzkosten m, links Monopol, rechts bei
Preisdiskriminierung zweiten Grades
43 / 88
Preisdifferenzierung 3. Grades
Gewinnfunktion des Monopolisten, der P. dritten Grades betreibt:
Π(x1 , x2 ) = p1 (x1 )x1 + p2 (x2 )x2 − C (x1 + x2 )
zwei FOC:
∂Π(x1 , x2 )
= MR1 (x1 ) − MC (x1 + x2 ) = 0
∂x1
∂Π(x1 , x2 )
= MR2 (x2 ) − MC (x1 + x2 ) = 0
∂x2
Anmerkung: daraus ergibt sich, dass Grenzerlöse gleich sein
müssen; sonst könnte eine Einheit vom einen Markt zum anderen
umgeschichtet werden, Erlös gesteigert, aber Kosten konstant
gehalten werden
44 / 88
Preisdifferenzierung Graphisch
Grenzerlöse müssen gleich sein, Lösung z.B. bei konstanten
Grenzkosten:
Anmerkung: da es sich um 2 parallele Monopolsitutation handelt,
kann die Lösung wieder als Preis- oder Mengenwahl formuliert
werden
45 / 88
Preisdifferenzierung 3. Grades, Beispiele
weitere Beispiele:
I
Flugticketpreis abhängig davon, ob die Reise ein Wochenende
umschließt; Dienstreisende haben oft höhere
Zahlungsbereitschaft, reisen aber nicht am Wochenende
I
Rabattmarken, die Kunden mit niedriger Zahlungsbereitschaft
bereit sind auszuschneiden und zu sammeln, Kunden mit
höherer Zahlungsbereitschaft aber lieber den Normalpreis
zahlen als sich um Sammlung zu kümmern
I
intertemporale P., wenn ein Produkt kurzfristig im Angebot
ist und sich preissensible Kunden über solche Situationen
informieren, während weniger preissensible Kunden kaufen
wann sie wollen (oder sogar Ansturm vermeiden wollen)
I
Produkt mit Markenname, und Verkauf des gleichen Produkts
als No-Name-Produkt
46 / 88
Voraussetzungen für P. Dritten Grades
nur möglich wenn:
I
Firma hat Marktmacht, sonst kann nicht mehr als der
Wettbewerbspreis verrechnet werden
I
Konsumentengruppen sind unterschiedlich und differenzierbar:
spezielle Charakteristika einer Gruppe, z.B. Alter
(Personalausweis), unterschiedliche Länder, Mechanismus der
Selbstauswahl (etwa höhere Kosten für Telefonbestellungen,
wenn jmd. keine Zeit verlieren will und sich nicht anstellen
will; oder Flugticketsbsp.)
I
Wiederverkauf ist unmöglich oder begrenzt
47 / 88
Preisdifferenzierung: Beispiel (1)
Inverse Nachfragefunktionen auf 2 differenzierbaren Märkten,
Kostenfunktion des Monopolisten:
p1 = 200 − 2x1 ,
p2 = 100 − x2 ,
C (x1 , x1 ) = 20 · (x1 + x2 )
Nachfrage in den Segmenten in Abhängigkeit vom Preis:
x1 = 100 − p1 /2,
x2 = 100 − p2
Erlös in den Segmenten:
R1 (p1 ) = p1 x1 = p1 (100−p1 /2),
R2 (p2 ) = p2 x2 = p2 (100−p2 )
Gewinnfunktion als Funktion der Preise in den Segmenten
Π(p1 , p2 ) = R1 (p1 ) + R2 (p2 ) − 20(200 − p1 /2 − p2 )
48 / 88
Preisdifferenzierung: Beispiel (2)
p1
60
80
100
120
140
4000
G
2000
0
20
60
40
80
0
100
p2
49 / 88
Preisdifferenzierung: Beispiel (3)
Optimalitätsbedingungen:
∂Π !
=0
∂p1
,
∂Π !
=0
∂p2
Optimale Preisdifferenzierung:
p1 = 110,
x1 = 45,
p2 = 60,
x2 = 40.
Optimaler Gewinn des Produzenten
Π(110, 60) = 5650
50 / 88
Preisdifferenzierung: Beispiel (4)
Was ist, wenn Preisdifferenzierung verboten bzw. nicht möglich
ist? D.h., wenn ein gemeinsamer Preis gesetzt werden muss?
Gemeinsame Nachfragefunktion, die aus der aggregierten
Nachfrage aus beiden Segmenten besteht
Nachfrage aus den Segmenten:
x1 = 100 − p/2,
p ∈ [0, 200],
x2 = 100 − p,
p ∈ [0, 100].
51 / 88
Preisdifferenzierung: Beispiel (5)
Aggregierte Nachfrage:
p ∈ [0, 100] :
p ∈ [100, 200] :
x = x1 + x2 = 200 − 3p/2,
x = x1 = 100 − p/2.
x
200
150
x1 +x2
100
50
x1
50
100
150
200
p
52 / 88
Preisdifferenzierung: Beispiel (6)
Oder p als eine Funktion des Absatzes:
x ∈ [0, 50] :
p = 200 − 2x,
x ∈ [50, 200] :
p = 2(200 − x)/3.
p
200
150
100
50
50
100
150
200
x
53 / 88
Preisdifferenzierung: Beispiel (7)
Gewinnfunktion ohne Preisdifferenzierung
x(200 − 2x) − 20x
: x ∈ [0, 50],
Π(x) =
2x(200 − x)/3 − 20x : x ∈ [50, 200].
G
4500
4000
3500
25
50
75
100
125
150
x
54 / 88
Preisdifferenzierung: Beispiel (8)
Ergebnis ohne Preisdifferenzierung:
p = 76 23 ,
x1 = 61 32 ,
x
x2 = 23 13 ,
=
85,
Π = 4816, 67.
55 / 88
Überblick: Marktstruktur und Charakteristika
Bedingung Π-max
Preissetzg. mögl.
Market power
Eintritt
No. Firmen
Long-run Π
Strategydependent
Beispiel
Monopol
MR = MC
Preissetzer
p > MC
Keiner
1
≥0
Nein
(keine Rivalen)
Oligopol
MR = MC
Preissetzer
p > MC
Beschränkt
Wenige
≥0
Ja
Lokaler Erdgasanbieter
Autohersteller
Wettbewerb
p = MR = MC
Preisnehmer
p = MC
Frei
Viele
0
Nein
(nur Marktpreis
relevant)
Obstproduzent
56 / 88
Strategische Interaktionen
Kooperation mehrerer Firmen
I
Kartelle
Nicht-kooperative Oligopole
Mengenwettbewerb
I
Cournot-Modell
I
Stackelberg-Modell
Preiswettbewerb
I
Bertrand-Modell
57 / 88
Preiswettbewerb
Oligopol-Modell nach Bertrand (1883); Firmen konkurrieren über
die Festlegung ihres Marktpreises;
I
Homogenitätsannahme (Güter gleich)
I
keine Kapazitätsbeschränkungen
→ nur niedrigster Preis kann sich als Marktpreis behaupten,
p = min(AC )
ähnlich dem Modell des vollständigen Wettbewerbs, doch Resultat
des geringsmöglichen“ Gleichgewichtspreises ergibt sich auch bei
”
wenigen Firmen (schon ab n = 2), nicht erst bei sehr vielen“
”
58 / 88
Simultaner Preiswettbewerb
Analyse des Falls mit 2 Firmen, Duopol; Grundstruktur:
Modell: Duopol, lineare Nachfrage, Grenzkosten konstant
X (p) = d − ep,
Ci (Xi ) = ci Xi ,
i ∈ 1, 2
Zusätzliche Annahme: bei gleichen Preisen, Halbierung der
Nachfrage
59 / 88
Preis-Absatz-Funktion, Gewinnfunktion
Preis-Absatz-Funktion für U1:

 d − ep1 wenn p1 < p2
d−ep1
x1 (p1 , p2 ) =
wenn p1 = p2
 2
0
wenn p1 > p2
Gewinnfunktion für U1:
Π1 (p1 , p2 ) = (p1 − c1 )x1 (p1 , p2 )
Symmetrisch für U2
60 / 88
Bertrand-Gleichgewicht
Zusätzliche Annahme: c1 = c2 = c < d/e
Preis kann beliebig kontinuierlich gewählt werden
I
p1 < c: Verluste
I
p1 > c: U2 kann p2 = p1 − setzen und bedient den ganzen
Markt mit Gewinn
I
die vorherige Situation ist aber kein Gleichgewicht (GGW), da
U1 ebenfalls U2 um unterbieten kann und Π1 von Null auf
einen positiven Wert erhöht
I
usw.
I
erst (p1 , p2 ) = (c, c) ist ein GGW
61 / 88
Bertrand-Gleichgewicht
GGW:
(p1B , p2B ) = (c, c)
Daraus ergibt sich:
d − ec
1
x1B = x2B = X (p = c) =
2
2
Die Gewinne sind Null:
B
B
B
ΠB
1 = Π2 = (p − c) x = 0
| {z }
0
62 / 88
Diskussion der Alternativen
1. (p1 , p2 ) = (c + δ, c + δ), δ > 0, c + δ < d/e; unterbieten führt
zu Verringerung des Stückgewinns, aber Verdoppelung des
Absatzes; kein GGW
2. (p1 , p2 ) = (c + δ, c + γ), γ > δ > 0, c + δ < d/e; dann gilt
Π2 (p1 , p2 ) = 0, und U2 kann durch c < p2 ≤ c + δ einen positiven
Profit erzielen; kein GGW
3. (p1 , p2 ) = (c + δ, c), δ > 0; U2 bedient den ganzen Markt, hat
aber Π2 (p1 , p2 ) = 0; U2 kann wieder einen positiven Profit
erreichen, und zwar durch c < p2 ≤ c + δ; kein GGW
nur (c, c) bleibt als GGW
Anmerkung: wenn z.B. p1 > p M , dann ist der optimale Preis p2
des anderen Duopolisten der Monopolpreis, p M = d+ce
2e , anstatt
das bloße unterbieten um 63 / 88
Adaptionen des Bertrand-Modells
Bertrand-Modell läßt sich an geänderte Rahmenbedingungen
anpassen; z.B.:
I
ein Unternehmen kann aufgrund einer
Kapazitätsbeschränkung nicht die ganze Nachfrage bei p = c
bedienen; Konsequenz: andere Unternehmen können dann das
Gut den restlichen Kunden zu einem höheren Preis verkaufen
I
Kostenführerschaft im Bertrand-Duopol: kostengünstigeres
Unternehmen kann sich allein auf dem Markt behaupten, aber
möglicherweise (je nach Kostendifferenz) nicht wie ein
Monopolist verhalten ( abgeschreckter Eintritt“)
”
64 / 88
Preiskartell im Bertrand-Duopol
wenn cj < piM , d.h. Unternehmen i kann nicht den Monopolpreis
setzen, dann ist es profitabel für beide, gemeinsam den
Monopolpreis durch Absprache festzulegen und die Gewinne zu
teilen
relevante Fälle: c2 ∈ [c1 , p1M ], c1 < d/e
65 / 88
Diskussion der Kartellmöglichkeiten
Problem: Kartell profitabel, aber kein GGW, denn Abweichung auf
p = p M − ist aus Sicht jeder einzelnen Firma eine Verbesserung;
Problem praktisch: Kartellabsprachen sind verboten, und daher
sind einklagbare Vereinbarungen unmöglich; andererseits, wenn
Kartellabsprache möglich (legal) ist, wie bei der OPEC (Kartell),
dann weil es keine internationale, verbindliche Rechtssprechung
gibt, und dann fehlt wieder die rechtliche Möglichkeit der
Sanktionierung; Beobachtung: bei der OPEC kommt es immer
wieder zu Abweichungen von den Absprachen
Anmerkung: potentieller Markteintritt unterminiert wegen hoher
Profite die Stabilität; allerdings ist diese Problem geringer, wenn es
Markteintrittsbarrieren gibt, idealerweise natürliche wie
geographische Verteilung und Größe von Rohstoffvorkommen”;
”
toll (für die OPEC), denn das trifft auf sie zu
66 / 88
Cournot-Modell des nicht-kooperativen Oligopols
I
nach Cournot (1838)
I
Firmen wählen die produzierte Menge zur gleichen Zeit
I
Firma wählt Output, bevor sie die Outputmenge der
Konkurrenz kennt
I
Firma kann jede beliebige Menge wählen, um Gewinn zu
maximieren
I
Nicht-kooperatives Verhalten mit unvollständiger Information
Modell
I
Duopol: 2 Firmen
I
Identische Produkte
I
Ein-Perioden-Markt (Lagerhaltung nicht möglich)
67 / 88
Cournotmodell
Firmen entscheiden über Produktionsmenge, die sie auf den Markt
bringen; Preis bildet sich entsprechend der Nachfrage, gegeben die
Gesamtmenge am Markt
Gewinn:
Π1 (x1 , x2 ) = p(x1 + x2 )x1 − C1 (x1 )
p(X ) ist die inv. Nachfragefkt., X = x1 + x2 Marktoutput, Kosten
hängen natürlich nur von eigener Produktion x1 ab; linearer Fall:
Π1 (x1 , x2 ) = (a − b(x1 + x2 )) x1 − c1 x1
68 / 88
Reaktionsfunktion
Konzept der besten Antwort“, aus der Spieltheorie; Ziel ist
”
Gewinnmaximierung; z.B. für Unternehmen 1: gegeben der
Mitspieler (Konkurrenten, Unternehmen 2) wählt eine bestimmte
Aktion (Mengenwahl, x2 ), was ist die eigene optimale Aktion
(ideale Mengenwahl, x1 )?
bezeichne die jeweils beste Antwort“, die in Abhängigkeit des
”
Verhaltens des anderen Unternehmens steht, so:
x1R (x2 )
b.A. ist eine Funktion der Aktion des anderen Unternehmens; R.
steht für Reaktion“, x1R wird auch Reaktionsfunktion“ genannt
”
”
69 / 88
Reaktionsfunktion Cournotmodell
Was ist die b.A. von x1 auf x2 , um Π1 möglichst groß zu machen?
x1R (x2 ) = arg max Π(x1 , x2 )
x1
Erlös: R(x1 , x2 ) = p (X (x1 , x2 )) x1 , Grenzerlös:
∂R(x1 , x2 )
dp ∂X
= p + x1
∂x1
dX ∂x1
wobei
∂X
∂(x1 + x2 )
∂x1 ∂x2
=
=
+
=1+0
∂x1
∂x1
∂x1 ∂x1
die Outputerhöhung von U2 ist Null, da U2 im simultanen
Wettbewerb nicht auf x2 reagieren kann
70 / 88
Reaktionsfunktionen im Linearen Fall
∂Π1
!
= (a − b(x1 + x2 )) + x1 (−b) − c1 = 0 ⇒
∂x1
a − c1 x2
x1R (x2 ) =
−
und wegen der Symmetrie,
2b
2
a − c2 x1
−
x2R (x1 ) =
2b
2
d.h. wenn U1 erwartet, dass U2 seine Menge um eine Einheit
erhöht, dann sinkt die gewinnmaximierende Menge von U1 um 0,5
Einheiten
1
dx1R /dx2 = −
2
71 / 88
Darstellung der Reaktionsfunktionen und des
Cournot-Nash-Gleichgewichts (CNG)
am Bsp. c1 = c2 = c:
alle Punkte auf den beiden Geraden sind b.A., aber nur ein Punkt
ist eine Strategiekombination, die eine wechselseitige b.A..
darstellt; der Schnittpunkt ist daher das (einzige) CNG
72 / 88
Schnittpunkt
Schnittpunkt x1R (x2 ) = x2R (x1 ):
x1C =
3 C
x =
4 1
x1C =
x2C =
=
=
=
a − c1 1 a − c2 1 C
−
− x1
2b
2
2b
2
2a − 2c1 − a + c2
4b
1
(a − 2c1 + c2 )
3b
a − c2 1 1
−
(a − 2c1 + c2 )
2b
2 3b
3a − 3c2 − a + 2c1 − c2
6b
2a − 4c2 + 2c1
6b
1
(a − 2c2 + c1 )
3b
muss auch analog ausschauen wegen Symmetrie
73 / 88
Lösung der Restlichen Variablen
X C = x1C + x2C =
1
(2a − c1 − c2 )
3b
1
p C = (a + c1 + c2 )
3
1
C
Π1 =
(a − 2c1 + c2 )2
9b
1
ΠC2 =
(a − 2c2 + c1 )2
9b
man sieht auch: ∂ΠCi /∂a > 0, und ∂ΠCi /∂b < 0, d.h. Erhöhung
der Zahlungsbereitschaft wirkt sich positiv auf die Gewinne aus;
Anwendung: eine koordinierte industrieweite Werbekampagne kann
zu einer Erhöhung von a oder Senkung von b führen und für alle
Produzenten lohnen (z.B. Fleisch bringts”-Werbung der AMA)
”
74 / 88
Kartell im Mengenmodell
Kartelllösung entspricht der Monopollösung; zu beachten sind:
I
nur Produktion zu niedrigst möglichen Grenzkosten ist
profitmaximierend
I
Kartellgewinn muß bei unterschiedlichen Grenzkosten so
aufgeteilt werden, dass die Anreize zur Kartellabsprache
erhalten bleiben
I
Kontroll- (zur schnellen Entdeckung eines
Abmachungsbruchs) und Sanktionsmechanismen (schwierig
bei Rechtswidrigkeit von Kartellen) können festgelegt werden
aber Einhaltung ist schwierig, wegen inhärenter Instabilität
75 / 88
Absprache und Abweichung Graphisch
keine einzige Outputkombination (außer die Randpunkte) die zur
Kartellmenge führt, liegt auf der Reaktionsfkt. auch nur eines
Unternehmens
76 / 88
Stackelberg-Modell
Modell des sequentiellen, nicht-kooperativen Mengenwettbewerbs,
von Stackelberg (1934); erster Duopolist wählt Menge, ist der
Stackelberg-Führer”, Zweier, der Stackelberg-Folger”,
”
”
beobachtet das, und antwortet mit seiner Menge, aber jetzt nicht
simultan sonder in Zeitperiode zwei:
Stackelberg-Führer
1. Überlegt sich Reaktionsfkt. des Folgers, i.e. dessen
Profitmaximum
2. Berechnung der eigenen optimalen Menge unter
Berücksichtigung der Reaktionsfkt. des Folgers
3. Wahl der Menge
→ Folger wählt entsprechend seiner Reaktionsfkt.
Gewinnfunktionen wie bei Cournot, aber Lösung jetzt durch
Rückwärtsinduktion; zweite Stufe bleibt gleich:
a − c2 1
x2R (x1 ) = arg max Π2 (x1 , x2 ) =
− x1
x2
2b
2
77 / 88
Erste Stufe des Führers
Stackelberg-Führer kann x2 beeinflußen und sich aus x2R (x1 ) ein x2
aussuchen; d.h. er berücksichtigt seinen Einfluß auf x2 explizit:
Π1 x1 , x2R (x1 ) = p x1 + x2R (x1 ) x1 − c1 x1
im linear-linearen Fall:
a − c2 1
R
Π1 x1 , x2 (x1 ) = a − b x1 +
− x1
− c1 x1
2b
2
1
= (a − bx1 + c2 − 2c1 )x1
2
1
1
!
dΠ1 /dx1 = (−b)x1 + (a − bx1 + c2 − 2c1 ) = 0 ⇒
2
2
a + c2 − 2c1
S
x1 =
2b
78 / 88
Lösung Graphisch und Vergleich Cournot
beachte: x1R (x2 ) ist für Stackelberg-Modell unbedeutend; in
Cournot ist x1S nicht b.A. auf x2S , aber in Stackelberg-Modell
trotzdem optimal; Grund: x1R (x2 ) berücksichtigt nicht dass U2 bei
x1R (x2S ) abweichen wird von x2S
79 / 88
Lösung Restliche Variablen
Lösungen für (x1S , x2R ):
x1S =
x2S =
XS =
p(X S ) =
ΠS1 =
ΠC2 =
a − 2c1 + c2
2b
a + 2c1 − 3c2
4b
3a − 2c1 − c2
4b
1
(a + 2c1 + c2 )
4
1
(a − 2c1 + c2 )2
8b
1
(a − 3c2 + 2c1 )2
16b
80 / 88
Beispiel (1)
2 Fluglinien, die eine Route bedienen: AA, American Airlines, UA,
United Airlines
Nachfragefkt: Q = 339 − p (in tsd. Flügen pro Quartal), MC = 147
Monopolverhalten:
81 / 88
Beispiel (2)
Ziel: Reaktion des einen ist optimal gegeben die Aktion des
anderen, und umgekehrt; das gilt dann, wenn sich die
Reaktionsfunktionen schneiden
Zuerst Aufstellen der Reaktionsfunktionen, RUA und RAA ;
Nachfrage für UA
p = 339 − qAA − qUA
Profitmaximierung für UA
ΠUA = p(Q)qUA − C (qUA )
= (339 − qAA − qUA )qUA − 147 · qUA
!
Π0UA = 339 − qAA − 2qUA − 147 = 0
−147
∗
= qUA
⇒ qUA = 339−qAA
2
qAA
= RUA = 96 − 2
analoge Berechnung:
RAA = 96 −
qUA
2
82 / 88
Beispiel (3)
Variieren von qUA → Funktion für qAA als beste Antwort“ für
”
jedes beliebige qUA
I
I
I
I
Nur eine Firma produziert bei qUA oder qAA gleich 96
(hypothetisch)
Gleichgew. bei Duopol bei qUA = qAA = 64
(hypothetischer) Marktaustritt des anderen bei 192
Prozess strebt“ immer zum GGW, im Schnittpunkt stabil
”
83 / 88
Beispiel (4)
System der Reaktionsfunktionen:
RUA = 96 −
RAA = 96 −
qAA
2
qUA
2
Schnitt von RUA und RAA ist Gleichgewicht
qUA
qUA
qUA
qAA
=
=
=
=
96 −
48 +
64
96 −
qUA
2
96−
2
qUA
4
64
2
= 64
Marktpreis und Profite ergeben sich wie üblich (Beachte: beide
Firmen sind gleich)
p(Q) = p(qUA + qAA ) = 339 − 128 = 211
ΠUA = pqUA − C (qUA ) = 211 · 64 − 147 · 64 = 4096
84 / 88
Beispiel (5): Kartelllösung
Beim Kartell entscheiden die (beiden) Firmen, die gemeinsamen
Profite zu maximieren
Entspricht der Monopollösung
MR(Q) = 339 − 2Q
MC (Q) = 147
MR = MC ⇒ Q ∗ = 96
Marktpreis ist
p(Q) = 339 − 96 = 243
Gemeinsamer Profit ist
ΠUA = 243 · 96 − 147 · 96 = 9216
und das ist mehr als die Summe der Duopolgewinne:
2 · 4096 = 8192 < 9216
85 / 88
Beispiel (6): Stackelberg, A Führer, U Folger
Reaktionsfunktion des Folgers unterscheidet sich nicht
96 − qA /2 für qA ≤ 192
RU =
0
für qA > 192
Führer nimmt Verhalten des Folgers aber direkt auf; das ergibt für
den Produktionsbereich von A die inverse Nachfrage:
p(Q = qU + qA ) = 339 − qA − qU
= 339 − qA − 96 + 1/2qA
= p = 243 − 1/2qA
. . . und somit für den ganzen Bereich
243 − 1/2qA für qA ≤ 192
p=
339 − qA
für qA > 192
86 / 88
Beispiel (7): Stackelberg, Graphisch
87 / 88
Beispiel (8) Stackelberg, Lösung
Suche Profitmaximum:
ΠA = p qA + qU (qA ) · qA − qA · C (qA )
!
Π0A = 0 ⇒ qA∗
Für das Beispiel
ΠA
=
=
Π0A =
qA =
qU =
p =
⇒
(339
− qA − qU ) · qA − 147q
A
339 − qA − (96 − qA /2) qA − 147qA
339 − 2qA − 96 + 2qA /2 − 147 = 0
96
96 − qA /2 = 48
195
ΠA = 4608, ΠU = 2304
88 / 88