I. Grundlagen: Datenverwaltung, grundlegende Operationen

Statistik I – R
WS 2001/02
I. Grundlagen: Datenverwaltung, grundlegende Operationen:
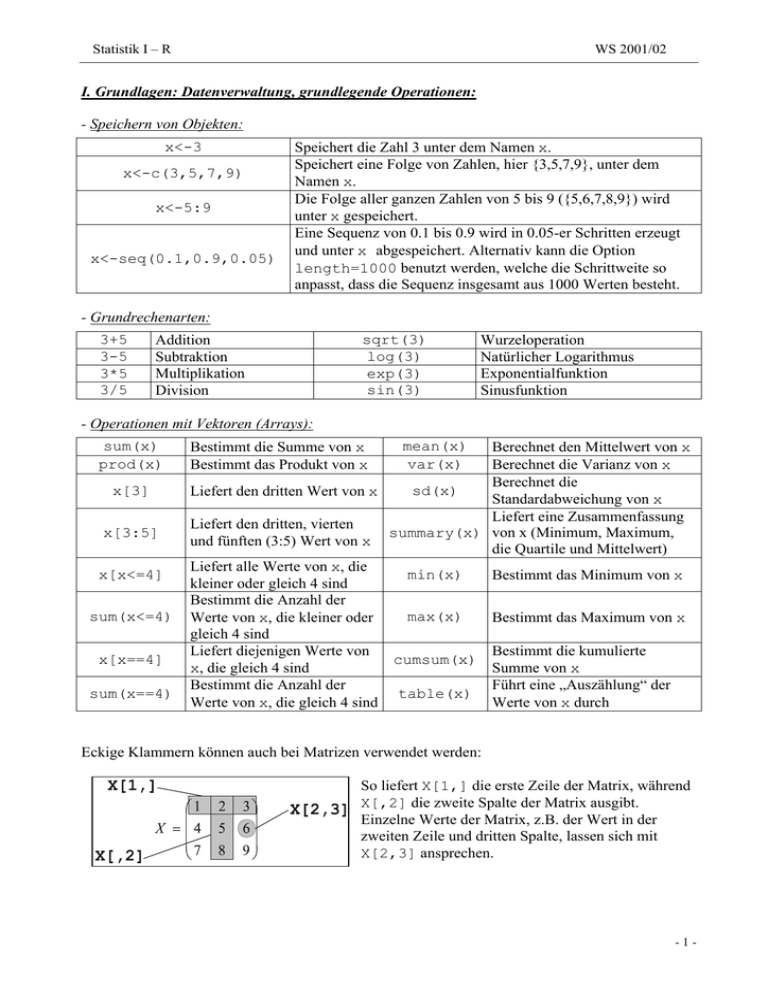
- Speichern von Objekten:
x<-3
x<-c(3,5,7,9)
x<-5:9
x<-seq(0.1,0.9,0.05)
Speichert die Zahl 3 unter dem Namen x.
Speichert eine Folge von Zahlen, hier {3,5,7,9}, unter dem
Namen x.
Die Folge aller ganzen Zahlen von 5 bis 9 ({5,6,7,8,9}) wird
unter x gespeichert.
Eine Sequenz von 0.1 bis 0.9 wird in 0.05-er Schritten erzeugt
und unter x abgespeichert. Alternativ kann die Option
length=1000 benutzt werden, welche die Schrittweite so
anpasst, dass die Sequenz insgesamt aus 1000 Werten besteht.
- Grundrechenarten:
3+5
3-5
3*5
3/5
Addition
Subtraktion
Multiplikation
Division
sqrt(3)
log(3)
exp(3)
sin(3)
Wurzeloperation
Natürlicher Logarithmus
Exponentialfunktion
Sinusfunktion
- Operationen mit Vektoren (Arrays):
sum(x)
prod(x)
x[3]
x[3:5]
x[x<=4]
sum(x<=4)
x[x==4]
sum(x==4)
Bestimmt die Summe von x
Bestimmt das Produkt von x
Berechnet den Mittelwert von x
Berechnet die Varianz von x
Berechnet die
sd(x)
Liefert den dritten Wert von x
Standardabweichung von x
Liefert eine Zusammenfassung
Liefert den dritten, vierten
summary(x) von x (Minimum, Maximum,
und fünften (3:5) Wert von x
die Quartile und Mittelwert)
Liefert alle Werte von x, die
min(x)
Bestimmt das Minimum von x
kleiner oder gleich 4 sind
Bestimmt die Anzahl der
max(x)
Bestimmt das Maximum von x
Werte von x, die kleiner oder
gleich 4 sind
Bestimmt die kumulierte
Liefert diejenigen Werte von
cumsum(x)
Summe von x
x, die gleich 4 sind
Bestimmt die Anzahl der
Führt eine „Auszählung“ der
table(x)
Werte von x, die gleich 4 sind
Werte von x durch
mean(x)
var(x)
Eckige Klammern können auch bei Matrizen verwendet werden:
So liefert X[1,] die erste Zeile der Matrix, während
X[,2] die zweite Spalte der Matrix ausgibt.
Einzelne Werte der Matrix, z.B. der Wert in der
zweiten Zeile und dritten Spalte, lassen sich mit
X[2,3] ansprechen.
-1-
Statistik I – R
WS 2001/02
Der sample – Befehl:
x
size
replace=TRUE
replace=FALSE
prob
sample(x, size, replace=FALSE, prob)
Der Datensatz, aus dem die Stichprobe gezogen werden soll
Der Stichprobenumfang (n)
Bestimmt, ob mit (replace=TRUE) oder ohne (replace=FALSE)
Zurücklegen gezogen werden soll.
Mit dieser Option können den einzelnen Elementen von x
unterschiedliche Wahrscheinlichkeiten zugeordnet werden. Wird hier
nichts angegeben, hat jedes Element von x diesselbe Wahrscheinlichkeit.
Beispiel: Simulation von 50 Würfelwürfen
# „Definition“ der Grundgesamtheit:
x<-1:6
# Würfelsimulation als Stichprobe aus den Zahlen {1,2,...,6} mit Zurücklegen:
stichpr<-sample(x,size=50,replace=T)
Zur Auszählung der absoluten Häufigkeiten der einzelnen Augenzahlen kann man entweder
sum(stichpr==1) (liefert die absolute Häufigkeit der Augenzahl 1) einzeln für alle
Augenzahlen oder table(stichpr) verwenden (table führt die Auszählung automatisch für
alle Ausprägungen durch).
II. Graphische Darstellung unter R:
- Der plot - Befehl:
x,y
type=“p“
plot(x,y,type=“p“)
Die zu zeichnenden Wertepaare
Hiermit wird die Art der Graphik bestimmt. Wird hierbei nichts
angegeben (type=“p“), werden Punkte bzw. Kreise zur
Darstellung verwendet. Mit type=“l“ werden Linien, mit
type=“s“ Treppenkurven und mit type=“h“ vertikale
Linien zur Darstellung verwendet.
25
20
0
5
10
y
15
20
15
10
5
# Definition der x-Werte:
x <- 0:5
# Zugehörige y-Werte (y=x2)
y <- x^2
0
Beispiel: Parabel
0
1
2
3
4
5
0
1
2
3
x
type="s"
type="h"
4
5
4
5
20
15
10
5
0
0
5
10
y
15
20
25
x
25
# Unterteilung d. Graphikfensters in 4 Bereiche:
par(mfrow=c(2,2))
# plot mit unterscheidlichen type-Optionen:
plot(x,y,type=“p“,main=“type=p“)
plot(x,y,type=“l“,main=“type=l“)
plot(x,y,type=“s“,main=“type=s“)
plot(x,y,type=“h“,main=“type=h“)
type="l"
25
type="p"
0
1
2
3
x
4
5
0
1
2
3
x
-2-
Statistik I – R
WS 2001/02
- Der hist - Befehl:
hist(x,prob=FALSE,breaks,plot=TRUE)
x
Der Datensatz, welcher als Histogramm dargestellt werden soll
Die Option prob bestimmt, ob absolute (prob=FALSE) oder
prob=FALSE
relative (prob=TRUE) Häufigkeiten zur Darstellung verwendet
prob=TRUE
werden sollen.
Mit der Option breaks können Klassengrenzen (als Vektor)
breaks
definiert werden
Die Option plot steuert, ob das Histogramm graphisch
plot=TRUE
dargestellt werden soll (plot=TRUE) oder ob eine tabellarische
plot=FALSE
Darstellung (plot=FALSE) erfolgen soll. Standardmässig ist
plot=TRUE.
Beispiel: Histogramm von 100 standardnormalverteilten
Zufallszahlen und angepasste Dichtefunktion:
0.1
Density
0.2
0.3
0.4
Histogram of stichpr
0.0
# 100 standardnormal# verteile Zufallszahlen:
stichpr<-rnorm(100,0,1)
# Histogramm mit relativen Hkt.:
hist(stichpr,prob=T)
# Anpassen der Dichtefunktion:
x<-seq(-3,3,length=1000)
mu<-mean(stichpr)
sigma<-sd(stichpr)
y<-dnorm(x,mu,sigma)
lines(x,y,lwd=2)
-2
-1
0
1
2
3
stichpr
- Der barplot - Befehl:
barplot(y,names=x)
Die Werte (z.B. relative Häufigkeiten oder Wahrscheinlichkeiten),
welche als Stabdiagramm dargestellt werden sollen
Die zugehörigen Ausprägungen
y
x
Beispiel: s. „Diskrete Verteilungen“ (nächste Seite)
- Der boxplot - Befehl:
x
boxplot(x)
Der Datensatz, welcher als Boxplot dargestellt werden soll
Monatliche Renditen von RWE und VW
Januar 1981 - Dezember 1993
0.005
0.000
-0.005
-0.010
boxplot(ren[,5],ren[,6])
-0.015
# Die Daten sind in einer Matrix ren gespeichert,
# die Renditen von RWE sind dabei in der 5. und
# die von VW in der 6. Spalte
0.010
Beispiel: Darstellung von Renditen als Boxplot
RWE
VW
-3-
Statistik I – R
WS 2001/02
III. Statistische Verteilungen unter R:
Allgemeines zur Syntax:
Die R-Befehle für statistische Verteilungen sind
einheitlich aufgebaut. Der erste Buchstabe des
jeweiligen Befehles (d, p, r, q) gibt dabei an, ob
eine Dichte- bzw. Wahrscheinlichkeitsfunktion (d:
density), eine Verteilungsfunktion (p: probability
density), Zufallszahlen (r: random numbers) oder
Quantile (q: quantiles) betrachtet werden. An den
ersten Buchstaben („Art der Verteilung“) wird die
R-Bezeichnung der Verteilung angefügt, z.B.
norm für die Normalverteilung.
Diskrete Verteilungen:
Folgende diskrete Verteilungen wurden in den Übungen behandelt:
Verteilung
Binomialverteilung
Hypergeometrische
Verteilung
Poissonverteilung
Wahrscheinlichkeitsfunktion
Verteilungsfunktion
Zufallszahlen
dbinom(x,size=n,prob=π)
pbinom(q,size,prob)
rbinom(n,size,prob)
dhyper(x,m=Ne,n=Nm,k=n)
phyper(q,m,n,k)
rhyper(nn,m,n,k)
dpois(x,lambda=λ)
ppois(q,lambda)
rpois(n,lambda)
Beispiel: 10maliges Werfen einer Münze (Binomialverteilung mit n=10 und π=0.5)
Binomialverteilung mit n=10 und pi=0.5
0.15
0.20
# Graphische Darstellung der
# Wahrscheinlichkeitsfunktion:
0.00
0.05
0.10
x<-0:10
y<-dbinom(x,size=10,prob=0.5)
barplot(y,names=x,space=2)
0
2
3
4
5
6
7
8
9
10
Verteilungsfunktion der Binomialverteilung
mit n=10 und pi=0.5
0.0
0.2
0.4
y
0.6
0.8
1.0
# Graphische Darstellung der
# Verteilungsfunktion
x<-0:10
y<-dbinom(x,size=10,prob=0.5)
plot(x,y,type=“s“)
1
0
2
4
6
8
10
x
# Berechnung von Wahrscheinlichkeiten:
# Die Wahrscheinlichkeit, genau 5 mal Kopf bei 10 Würfen zu erhalten:
dbinom(5,10,0.5)
# Die Wahrscheinlichkeit, weniger als 6 mal Kopf zu werfen P(X<6)=P(X≤5):
pbinom(5,10,0.5)
-4-
Statistik I – R
WS 2001/02
Stetige Verteilungen:
Verteilung
Rechteckverteilung
Normalverteilung
Student-tVerteilung
Exponentialverteilung
ChiquadratVerteilung
Dichtefunktion
dunif(x,min=a,max=b)
Verteilungsfunktion
punif(q,min,max)
Zufallsahlen
runif(n,min,max)
Quantile
qunif(p,min,max)
dnorm(x,mean=µ,sigma=σ
σ) pnorm(q,mean,sigma) rnorm(n,mean,sigma) qnorm(p,mean,sigma)
dt(x,df=ν)
pt(q,df)
rt(n,df)
qt(p,df)
dexp(x,rate=λ)
pexp(q,rate)
rexp(n,rate)
qexp(p,rate)
dchisq(x,df=ν)
pchisq(q,df)
rchisq(n,df)
qchisq(p,df)
Beispiel: Anpassung einer Normalverteilung an die Verteilung von monatlichen Renditen
Histogramm der monatlichen Renditen
(VW; 1981-1993)
100
# Die Renditen von VW sind in der 6.
# Spalte der Matrix ren gespeichert.
# Darstellung als Histogramm
80
daten<-ren[,6]
# Einzeichnen der angepassten
# Dichte über das Histogramm
x<-seq(-0.02,0.02,length=1000)
y<-dnorm(x,mu,sigma)
lines(x,y)
40
20
mu<-mean(daten)
sigma<-sd(daten)
0
# Anpassen der Normalverteilung
60
hist(daten,prob=T)
-0.015
-0.010
-0.005
0.000
0.005
0.010
0.015
# Berechnen von Wahrscheinlcihkeiten mit Hilfe der angepassten Normalverteilung:
# Die Wahrscheinlichkeit, daß die Rendite in einem Monat weniger als 0% ist:
pnorm(0,mu,sigma)
# Die Wahrscheinlichkeit, daß die Rendite in einem Monat zwischen 0% und 1% liegt:
pnorm(0.01,mu,sigma)-pnorm(0,mu,sigma)
# Bestimmung des 90%-Konfidenzintervalls für die erwartete Rendite (n=156)
# (->Konfidenzintervall für den Mittelwert bei unbekannter Varianz.)
xquer<-mean(daten)
sigmastern<-sd(daten)
# Quantil (hier: t-Verteilung)
quant<-qt(0.95,155)
# untere Grenze des Konfidenzintervalls:
xquer-quant*sigmastern/sqrt(156)
# obere Grenze des Konfidenzintervalls:
xquer+quant*sigmastern/sqrt(156)
-5-