¨Ubungen zur Einf¨uhrung in die Astronomie und Astrophysik II

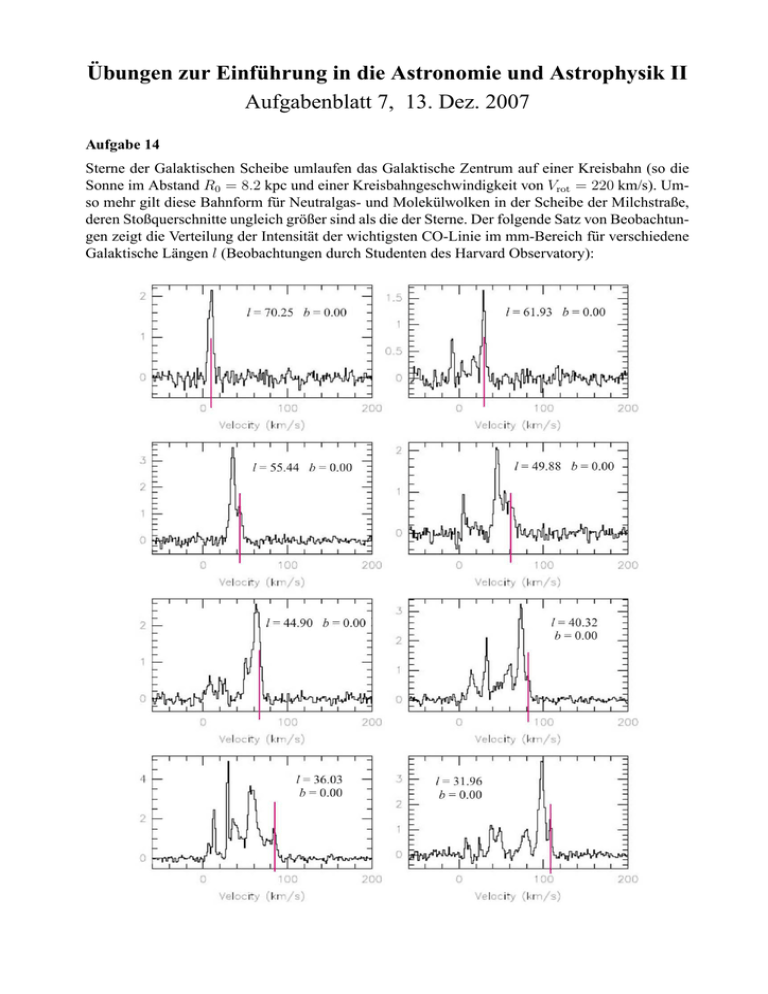
Übungen zur Einführung in die Astronomie und Astrophysik II
Aufgabenblatt 7, 13. Dez. 2007
Aufgabe 14
Sterne der Galaktischen Scheibe umlaufen das Galaktische Zentrum auf einer Kreisbahn (so die
Sonne im Abstand R0 = 8.2 kpc und einer Kreisbahngeschwindigkeit von Vrot = 220 km/s). Umso mehr gilt diese Bahnform für Neutralgas- und Molekülwolken in der Scheibe der Milchstraße,
deren Stoßquerschnitte ungleich größer sind als die der Sterne. Der folgende Satz von Beobachtungen zeigt die Verteilung der Intensität der wichtigsten CO-Linie im mm-Bereich für verschiedene
Galaktische Längen l (Beobachtungen durch Studenten des Harvard Observatory):
(a) Konstruieren Sie aus diesen Daten den dadurch zugänglichen Bereich der Rotationskurve der
Milchstraße und stellen Sie Vrot (R) als Funktion von R in einer Skizze dar. Geben Sie einen Mittelwert der beobachteten Umlaufgeschwindigkeiten an und vergleichen Sie das Ergebnis mit der
Rotationskurve nach Kepler (Gl. 273 im Vorlesungsmanuskript). [4 Punkte]
In den beobachteten Spektren der CO-Linien wird die nach der Tangentenmethode jeweils höchste
Geschwindigkeit markiert (siehe Abbildung oben). Aus der Umrechnung nach Gl. 628 und 629
erhält man eine Tabelle der Kreisbahngeschwindigkeiten Θ(R). Damit folgt die Rotationskurve
(nächste Seite).
Die wesentliche Eigenschaft der Galaktischen Rotationskurve ist ihre Konstanz über praktisch den
gesamten inneren Bereich, R < R0 . Diese erstreckt sich auch weiter nach außen bis mindestens
15 kpc.
Dies bedeutet, daß auch beim galaktozentrischen Abstand der Sonne (R0 ) ein großer Teil der gravitierenden Gesamtmasse der Milchstraße noch nicht erfaßt ist (also außerhalb liegen muß). Auch
die Rotationskurve der Milchstraße ist somit ein Indiz für die Existenz dunkler Materie.
(b) Welche Voraussetzungen sind für diese Methode nötig? Warum taugt diese Methode nicht zur
Verfolgung der Rotationskurve außerhalb R0 ? [2 Punkte]
300
Vrot = 214 ± 11 km/s
250
Θ(R)
200
Kepler−Rotation
150
100
50
0
0
2
4
R [kpc]
6
8
Um die Tangentenmethode eindeutig zu machen, ist es erforderlich, daß die größte beobachtete
Geschwindigkeit dem jeweils tangentialen Bogen zugeordnet werden kann. Die Emission der COLinie an diesem Abstand vom Galaktischen Zentrum wird dabei überlagert durch alle weiter außen
umlaufenden Molekülwolken. Besitzt deren tangentiale Bahngeschwindigkeitskomponente eine
Projektion, die größer ist als die tangentiale Geschwindigkeit weiter innen, so ist die eindeutige
Zuordnung nicht mehr möglich.
Wie die nebenstehende Skizze zeigt, besitzt die Wolke
mit R2 und Θ2 auf der Sehline die projizierte Komponente Θ = Θ2 cos φ2 . Aus dem Dreieck GC – Sonne –
Tangentialpunkt erhält man R2 cos φ2 = R0 sin l1 . Eine eindeutige Zuordnung der beobachteten Geschwindigkeiten ist daher nur möglich für
Θ2
Θ1
>
R1
R2
.
Nicht die Kreisbahngeschwindigkeiten Θ sondern die
Winkelgeschwindigkeiten ω = Θ/R müssen also monoton mit R fallen. Wie man leicht überlegt, gilt dies
auch für konstante oder sogar leicht ansteigende Kreisbahngeschwindigkeiten.
Keine Sehlinie mit 90◦ < l < 270◦ ist eine Tangente an
einen galaktozentrischen Kreis. Damit ist die eindeutige Bestimmung der Entfernung vom GC nicht mehr
möglich.
Aufgabe 15
Die spektroskopische Beobachtung von H II-Regionen
ergibt folgende Messungen für die Positionen der Hβ-Linie (4861.297 Å) und der [O III]-Linie
(5006.9 Å) bei Galaktischen Längen l:
l [◦ ]
71
101
119
138
165
λ [Å]
4861.51
4861.23
4861.18
4861.14
4861.18
λ [Å] l [◦ ]
5007.11
75
5006.83 107
5006.78 133
5006.74 164
5006.78 195
λ [Å]
4861.45
4861.19
4861.16
4861.19
4861.45
λ [Å]
5007.05
5006.79
5006.76
5006.78
5007.05
(a) Bestimmen Sie die Entfernungen der H II-Regionen. Nehmen Sie dabei eine mittlere Oortsche
Konstante A = 16 km/s/kpc an. Tragen Sie die Orte der H II-Regionen in eine Galaktische Karte
der Sonnenumgebung ein und diskutieren Sie das Ergebnis. [4 Punkte]
r(Hβ) [kpc]
1.333
0.688
0.530
0.607
0.900
r([O III]) [kpc]
1.276
0.698
0.573
0.601
0.899
Die Verknüpfung der gemessenen Radialgeschwindigkeit vr mit der Entfernung r
definiert die Oortsche Konstante A durch
vr = Ar sin 2l. Bei Kenntnis der Oortschen Konstante A läßt sich so (ohne große
Genauigkeit) die Entfernung aus der Radialgeschwindigkeit bestimmen, welche
wiederum aus dem Dopplereffekt folgt. Es
ergeben sich die Werte in der oben angegebenen Tabelle.
Die Lage der H II-Regionen ist in der nebenstehenden Abbildung dargestellt. Offensichtlich handelt es sich bei dieser Anordnung um Teile des Lokalen Spiralarms
in Richtung Perseus / Cassiopeia / Andromeda, der von der Sonne aus etwa 500
pc entfernt liegt. Die Galaktische Länge
l = 0◦ zeigt von der Sonne aus nach unten, die Länge l = 90◦ nach rechts.
l [◦ ] r(Hβ) [kpc]
75
1.182
107
0.737
133
0.528
164
0.778
195
1.182
r([O III]) [kpc]
1.122
0.735
0.526
0.848
1.122
1.0
Lokaler Spiralarm
0.5
kpc
l [◦ ]
71
101
119
138
165
0.0
-0.5
-0.5
Sonne
Galaktisches Zentrum
0.0
0.5
kpc
1.0
1.5
Aufgabe 16
Gilmore & Reid (1983) sind die Entdecker der dicken Scheibe. Sie beobachteten die Anzahl von
Sternen mit einer Absoluthelligkeit im Intervall MV = [4, 5] in verschiedenen Abständen z von
der Galaktischen Ebene. Die von ihnen gefundenen Werte sind für Intervalle zentriert auf log z
mit einer Intervallbreite von ∆ log z = 0.1 angegeben, wobei der erste der folgenden Werte für
ein Intervall gilt, das bei log(z/1pc) = 2.05 zentriert ist. Die Daten sind: 3, 7, 19, 22, 38, 50, 79,
107, 135, 149, 197, 207, 218, 233, 265, 301, 322. Hinweis: der zugrundeliegende Survey wurde
in einem Feld von 53.3 Quadratgrad durchgeführt, wodurch das entfernungsabhängige Volumen
begrenzt wird.
(a) Konstruieren Sie aus diesen Daten ein Diagramm der Anzahldichte ν als Funktion des Abstands von der Galaktischen Ebene in einem geeigneten Koordinatensystem und begründen Sie die
Existenz zweier Scheibenpopulationen. [5 Punkte]
Das geeignete Koordinatensystem ist das einer exponentiell fallenden Anzahldichte (siehe Scheibenpotentiale im Vorlesungsskript S. 88). Diese wird zur Geraden im einfach logarithmischen
Koordinatensystem.
Zur Berechnung der Anzahldichte muß für jedes Intervall ∆z berechnet werden, sowie die durch
das Surveyfeld bestimmte Fläche in der Entfernung√z. Nimmt man der Einfachheit halber ein quadratisches Bildfeld an, so ist dessen Kantenlänge 53.3 = 7.3◦ . Dieser Winkel entspricht einem
Tangens von 0.128, so daß in jeder Entfernung z das beobachtete Volumen sich näherungsweise
aus dem Produkt ∆z × (0.128z)2 zusammensetzt. Genauer geht es durch Differenzbildung von
Pyramidenstümpfen, aber der Unterschied ist marginal.
Die Anzahldichte wird anhand einer Division durch ein entsprechendes Volumen bestimmt und
logarithmisch über dem linearen Abstand z aufgetragen. Das Ergebnis ist in der folgenden Abbildung dargestellt.
-3
log ν [pc-3]
-4
-5
-6
0
1000
2000
3000
4000
5000
z [pc]
Die obenstehende Abbildung zeigt denn die Existenz zweier durch Geradenstücke approximierbarer Sternpopulationen. Die dünne Scheibe wird durch das linke Geradenstück approximiert, die
dicke Scheibe durch das rechte. Die Addition beider Beiträge liefert die gepunktete Kurve.