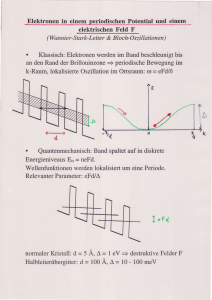
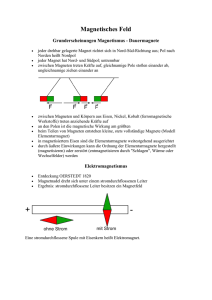
einfluss von kompensationsleitern auf die magnetische

EINFLUSS VON KOMPENSATIONSLEITERN AUF DIE
MAGNETISCHE ERSATZFLUSSDICHTE IN DER
UMGEBUNG ELEKTRISCHER BAHNEN
DIPLOMARBEIT
Institut für Elektrische Anlagen
an der
Technischen Universität Graz
Leitung : Univ.-Prof. Dipl.-Ing. Dr.techn. Lothar Fickert
Betreuung : Dipl.-Ing. Dr.techn. Ernst Schmautzer
Dipl.-Ing. Andreas Abart
Vorgelegt von: Peter Unterwieser
Graz, im Jänner 2005
Peter Unterwieser
Danksagung
Danksagung
Diese Diplomarbeit widme ich meiner Großmutter Johanna Unterwieser, meinen Eltern und
allen Verwandten, deren Unterstützung es mir ermöglichte dieses Studium und die
vorausgehende Schulausbildung erfolgreich abzuschließen. Ebenso möchte ich all meinen
Freunden danken die mir während meiner Studienzeit in Graz mit Rat und Tat zur Seite
standen.
Ich möchte mich bei Herrn Dipl.-Ing. Dr.techn. Ernst Schmautzer für die Betreuung und Hilfe
bei meiner Diplomarbeit bedanken. Weiters gilt Herrn Dipl.-Ing. Andreas Abart für die
Bereitstellung der Software MF-Calc-railway und die Erlaubnis, diese mit seiner Hilfe um den
Tunnelmodul zu erweitern, besonderer Dank. Auch bei den Österreichischen Bundesbahnen,
insbesondere Herrn Dr. Gerold Punz, seinen Mitarbeitern und der Dienststelle St. Pölten
möchte ich mich für die tatkräftige Unterstützung bei den Messungen am Grüntunnel
bedanken.
Abbildung 1.1 : Grüntunnel bei St.Pöllten
Peter Unterwieser
Kurzfassung
Kurzfassung
Deutsch
Ziel der Diplomarbeit ist es, den Einfluss von Reduktionsleitern auf das im Nahbereich von
elektrischen Eisenbahnen verursachte magnetische Feld zu bestimmen. Im Rahmen der
Diplomarbeit wurde ein Berechnungsmodul für elektrische Tunnelmodelle entworfen, wobei
der Einfluss der Reduktionsleiter, Schienen und Tunnelarmierungen bei der Feldberechnung
berücksichtigt wird. Die magnetischen Ersatzflussdichten werden mit Hilfe der Software MFCalc-railway für die Aufpunkte einer Schnittebene errechnet und visualisiert. Mit der
Möglichkeit magnetische Felder in Abhängigkeit von Reduktionsleitern zu berechnen, können
unterschiedliche Formen der Tunnelarmierungen und der Reduktionsleiteranordnung
miteinander verglichen werden. Für diesen Vergleich wurde eine Differenzdarstellung
entwickelt.
Ziel der Arbeit ist es, den Einfluss von Kompensationsleitern auf die Ersatzflussdichte in der
Umgebung von elektrischen Eisenbahnen zu beschreiben und Ansätze zu liefern, die es
gestatten die elektromagnetischen Emissionen zu minimieren.
English
The idea of this diploma thesis is to describe the influence of reduction conductors on
magnetic fields in case of electrical railways in the vicinity. For this software a new tunnel
module was developed to considerate the influence of reduction conductors on magnetic
fields. The magnetic flux density is calculated for the fieldpoints of a cross sectional plane
and its distribution visualised by a software called MF-Calc-railway. This tool allows to
compare different kinds of tunnel concrete reinforcements and reduction conductor
arrangements. For this comparison a graphic depicting the difference is developed.
The main target of this paper is to show the influence of reduction conductors on magnetic
fields in case of electrical railways and give ideas to minimize electromagnetic emissions.
Peter Unterwieser
Inhaltsverzeichnis
Inhaltsverzeichnis:
1
Einleitung....................................................................................................................... 6
1.1 Elektromagnetische Verträglichkeit ............................................................................... 6
2
Grundlagen der magnetischen Felder .......................................................................... 8
2.1 Entstehung und Berechnung magnetischer Felder ......................................................... 8
2.2 Physikalische Grundlagen .............................................................................................. 9
2.2.1
Das Biot-Savart’sche Gesetz.............................................................................. 9
2.2.2
Maxwell’sche Gleichungen.............................................................................. 11
2.3 Niederfrequente Magnetfelder bzw. ELF-Magnetfelder.............................................. 13
2.4 Berechnung magnetischer Felder ................................................................................. 14
2.4.1
Berechnung der Ersatzflussdichte nach ÖNORM S1119 ................................ 14
2.5 Grundlagen der Messung von elektromagnetischen Feldern ....................................... 15
2.5.1
Physikalische Zusammenhänge........................................................................ 15
2.5.2
Messverstärker ................................................................................................. 17
2.5.3
Messung zeitvarianter magnetischer Felder..................................................... 17
2.6 Prinzip und Problematik der verteilten Rückleitung .................................................... 23
2.7 Grenzwerte ................................................................................................................... 24
3
Programmierung ......................................................................................................... 25
3.1 Wie arbeitet MF-Calc-railway?.................................................................................... 25
3.2 Formelwerk zu MF-Calc-railway ................................................................................. 26
3.3 Grundsätzliche Überlegungen zur Tunnelsimulation................................................... 26
4
Rechenbeispiel zu MF-Calc-railway........................................................................... 34
4.1 Allgemeines.................................................................................................................. 34
4.2 Analytischer Rechenvorgang........................................................................................ 34
4.3 Berechnung mit MF-Calc-railway................................................................................ 40
5
Magnetfeldmessung Grüntunnel ................................................................................ 44
5.1 Allgemeines.................................................................................................................. 44
5.2 Spezielle Anforderungen an den Messtunnel ............................................................... 45
5.3 Die Ausführung der Messung....................................................................................... 46
5.4 Simulation des magnetischen Feldes bei Bahnanlagen unter Einfluss der
Tunnelarmierung .......................................................................................................... 49
5.5 Vergleich der Messung mit der Simulation.................................................................. 56
Peter Unterwieser
Inhaltsverzeichnis
5.5.1
6
Messung 1 in Querrichtung zur Tunnelachse................................................... 56
Reduktionsfaktorenrechnung mit MF-Calc-railway ................................................. 60
6.1 Allgemeines.................................................................................................................. 60
6.2 Reduktionswirkung an Hand eines Beispiels ............................................................... 63
6.3 Allgemeine Einflüsse auf die Reduktionswirkung ....................................................... 69
6.4 Reduktionswirkung auf der freien Stecke .................................................................... 72
6.5 Reduktionswirkung der Längsbanderder...................................................................... 75
6.6 Optimale geometrische Auslegung der Tunnelarmierung............................................ 79
6.7 Gedanken zur optimalen geometrischen Reduktionsleiteranordnung .......................... 84
7
Zusammenfassung und Ergebnisse ............................................................................ 91
8
Formelzeichen und Abkürzungen............................................................................... 93
9
Abbildungsverzeichnis................................................................................................. 95
10
Literaturnachweis........................................................................................................ 98
Peter Unterwieser
Einleitung
1 Einleitung
1.1 Elektromagnetische Verträglichkeit
Mit dem weit verbreiteten und immer noch zunehmenden Einsatz elektrotechnischer und
elektronischer Systeme hat sich die elektromagnetische Umwelt erheblich verändert. Neben
den seit jeher vorhandenen natürlichen Feldern hat die Stärke der vom Menschen erzeugten
Felder in der Umwelt, im Wohnbereich und besonders an den Arbeitsplätzen innerhalb kurzer
Zeit wesentlich zugenommen. Je nach Konzeption und Aufbau des jeweiligen Systems
reichen die Felder deutlich über sichtbare Systemgrenzen wie z.B. Gehäuse oder geschlossene
Räume hinaus in die Umgebung hinein. In der Nähe solcher Systeme können sich wiederum
andere Systeme befinden, für die die Felder des fremden Prozesses als Störgröße wirken. Je
nach Querempfindlichkeiten kann es zu gegenseitigen Beeinträchtigungen der Systeme
kommen, die eine bestimmungsgemäße Funktion stören. Als Konsequenz werden die Systeme
dann als elektromagnetisch unverträglich bezeichnet. Der Verlauf und die Größe der
magnetischen und elektrischen Felder in der Umgebung von elektrischen und elektronischen
Einrichtungen ist daher von großem Interesse für die störungsfreie Nachbarschaft von
Systemen. Neben der rein technischen elektromagnetischen Verträglichkeit wird auch in
zunehmendem Maß die Einwirkung elektrischer, magnetischer und elektromagnetischer
Felder auf Lebewesen berücksichtigt. In der Öffentlichkeit ist die Meinung verbreitet, dass
diese Felder für den Organismus schädlich sein könnten. Dass diese Felder im Allgemeinen
unseren Sinnen nicht direkt zugänglich sind, sondern gerechnet oder gemessen werden
müssen, fördert die Verunsicherung. Die Angst vor elektromagnetischen Feldern, die im
allgemeinen Sprachgebrauch auch als Elektrosmog bezeichnet werden, ist oft Ausgangspunkt
für eine Analyse. In der Tat bestehen auch von Seiten der Wissenschaft geringe Bedenken,
dass niederfrequente magnetische Felder ein Krebsgeschehen beeinflussen können. Allerdings
wurden jene Experimente, die dies bestätigen, mit magnetischen Wechselfeldern von 0.5 mT
durchgeführt1. Die durch Einrichtungen der Energietechnik in öffentlich zugänglichen
Bereichen verursachten Magnetfelder weisen typische Amplituden unter 5-10% des
Erdmagnetfeldes auf. Diese Relation ist allerdings nicht als unmittelbarer Vergleich zu
verstehen, sondern soll veranschaulichen, dass der resultierende Summenvektor im Fall der
1
BEMS 22th Annual Meeting 2000 Munich Abstract Book BEMS 2000.
Peter Unterwieser
Seite 6
Einleitung
Experimente nahezu ein reines Wechselfeld darstellt, während im Alltag der Summenvektor
der Vorstellung eines Pendels mit entsprechend geringem Ausschlag entspricht2. Mittlerweile
existieren normativ vorgegebene Grenzwerte, die auf gesicherten Erkenntnissen mit einem
gewissen Sicherheitszuschlag, beruhen. Diese Werte werden in der Regel, bei im Alltag
auftretenden Feldern, nicht erreicht. Jedoch kann die Einhaltung der Grenzwerte bei
vorliegenden Systemen praktisch nur messtechnisch erfasst werden, da insbesondere im Fall
der elektrischen Feldstärke Bewuchs, Feuchtigkeit oder metallische Strukturen erheblichen
und nahezu unkalkulierbaren Einfluss auf den Feldverlauf und die auftretenden Feldstärken
haben. Aber auch bei magnetischen Feldern ist es oft leichter, messtechnisch vorzugehen, als
für
ein
Objekt
alle
feldbeeinflussenden
Variablen
aufzunehmen
und
in
einem
Berechnungsprogramm zu modellieren. In der Planungsphase hingegen können nur
Berechnungen qualifizierte Aussagen über die zu erwartenden Feldstärken bzw. Flussdichten
liefern.
2
Larch J.: Niederfrequente magnetische Drehfelder in der elektrischen Energietechnik.
Peter Unterwieser
Seite 7
Grundlagen der magnetischen Felder
2 Grundlagen der magnetischen Felder
2.1 Entstehung und Berechnung magnetischer Felder
Ein magnetisches Feld entsteht immer dann, wenn elektrische Ladungen bewegt werden, d.h.
wenn elektrische Ströme fließen. Magnetische Feldlinien sind in sich geschlossen und
umschließen den feldverursachenden Strom. Bei einem stromdurchflossenen Leiter im
ungestörten Fall sind die Feldlinien konzentrische Kreise. Die magnetische Feldstärke H ist
umso größer, je größer der verursachende Strom ist. Die Frequenz mit der das magnetische
Feld sich ändert entspricht der Frequenz des verursachenden Stromes.
Das Feldlinienbild zeigt die charakteristischen konzentrischen Kreise. Die Dichte der Linien
r
des magnetischen Flusses B nimmt mit dem reziproken Wert des Abstands (entspricht dem
Radius) ab. Da der Strom I in Z-Richtung fließt, ist die Z-Komponente des Feldes null. Unter
der Voraussetzung eines unendlich langen, geraden, zylindrischen stromdurchflossenen
Leiters.
Abbildung 2.1 : Feldbild eines geraden einfachen Leiters
Peter Unterwieser
Seite 8
Grundlagen der magnetischen Felder
2.2 Physikalische Grundlagen
Grundlegende experimentelle Tatsachen und theoretische Überlegungen zum Thema
elektromagnetische Felder veranlassten im Jahr 1873 James Clark Maxwell zur Publikation
seiner Gleichungen in „A Treatise on Electricity and Magnetism“. Experimentelle Ergebnisse,
die sich auf den Zusammenhang zwischen dem auftretenden magnetischen Feld und dem
Strom beziehen, wurden jedoch schon zuvor von Biot und Savart im Biot-Savart’schen Gesetz
beschrieben.
2.2.1 Das Biot-Savart’sche Gesetz
r μI dsr × rr
⋅
B=
4π ∫s r 3
GL. 2.1
Nach dem Biot-Savart’schen Gesetz kann die magnetische Flussdichte eines beliebigen
Aufpunkts im Raum durch Integration entlang der feldverursachenden, geschlossenen
Leiteranordnung eines linearen Stromkreises berechnet werden.
Die differentielle Form des Biot-Savart’schen Gesetzes erlaubt die Interpretation, dass jedes
Leiterelement (fadenförmiger Leiter) der Schleife für sich ein magnetisches Feld erzeugt.
r μI dsr × rr
dB =
⋅ 3
4π
r
GL. 2.2
Abbildung 2.2 : Stromfaden in Z-Richtung von –l/2 bis +l/2
Peter Unterwieser
Seite 9
Grundlagen der magnetischen Felder
Das resultierende Feld ergibt sich aus der Superposition der durch einzelne Leiterelemente
r
ds verursachten Felder.
r
r
B = ∫ dB
GL. 2.3
Um die Wirkung eines magnetischen Feldes ausreichend zu beschreiben, muss jedoch auch
die Eigenschaft des Mediums berücksichtigt werden, in dem sich das magnetische Feld
ausbreitet. Aus diesem Grund wurde die magnetische Flussdichte B eingeführt, in der die
magnetische Materialeigenschaft, die Permeabilität μ erfasst ist.
r
r
B = μ⋅H
GL. 2.4
r
H ... magnetische Feldstärke [A/m]
r
B ... magnetische Flussdichte [T]
μ ... Permeabilität [Vs/Am]
Die Gleichung (Gl. 2.4) bringt zum Ausdruck, dass bei gleicher magnetischer Feldstärke die
magnetische Flussdichte umso größer ist, je größer die Permeabilität ist. Die Flussdichte ist
der auf eine Fläche bezogene magnetische Fluss. Die Einheit der magnetischen Flussdichte ist
Tesla bzw. Gauß, wobei gilt: 1 Tesla =10000 Gauß. Je nachdem wie sich Materialien im
magnetischen Feld verhalten unterscheidet man:
•
diamagnetische Stoffe, deren Moleküle sich im magnetischen Feld so ausrichten, dass
es zu einer Schwächung des Feldes kommt;
•
paramagnetische Stoffe, deren Moleküle sich im Magnetfeld so ausrichten, dass es zu
einer Verstärkung des Feldes kommt; und
•
ferromagnetische Stoffe wie Eisen, die eine große Feldverstärkung bewirken.
Peter Unterwieser
Seite 10
Grundlagen der magnetischen Felder
2.2.2 Maxwell’sche Gleichungen
Auf Basis der Maxwellschen Gleichungen3 kann die gesamte Elektrodynamik mathematisch
beschrieben werden.
I.
r
r r ∂D
rotH = J +
∂t
II.
r
r
∂B
rotE = −
∂t
III.
IV.
GL. 2.5
r
divD = ρ
r
divB = 0
und die Materialgleichungen
r
r
B = μ0 ⋅ μr ⋅ H
GL. 2.6
r
r
D =ε ⋅E
Für den stationären Fall, bei dem keine zeitlichen Veränderungen auftreten, vereinfacht sich
die Gleichungen in (2.5) zu (2.7). Weiters werden noch die Materialgleichungen eingesetzt.
I.
r
r
rotB = μ ⋅ J
II.
r
rotE = 0
III.
r ρ
divE =
IV.
r
divB = 0
GL. 2.7
ε
Ein stationäres magnetisches Feld, an einem beliebigen Punkt (Aufpunkt) mit den
Koordinaten X, Y und Z kann als Vektorfeld durch die Vektorkomponenten beschrieben
werden. Diese wiederum sind Funktionen der Koordinaten des Aufpunkts X, Y und Z.
3
Biro, O.: Vorlesungsskriptum Theorie der Elektrotechnik 2. TU Graz, Institut IGTE. 2001.
Peter Unterwieser
Seite 11
Grundlagen der magnetischen Felder
Abbildung 2.3 : Magnetisches Vektorfeld im Aufpunkt A(X, Y, Z)
⎛ B x ( x, y , z ) ⎞
r
⎜
⎟
B ( x , y , z ) = ⎜ B y ( x , y , z )⎟
⎜ B ( x, y , z ) ⎟
⎝ z
⎠
GL. 2.8
Niederfrequente Vorgänge, wie sie in der elektrischen Energietechnik vorkommen, lassen
eine Vereinfachung der I. Maxwell’schen Gleichung (2.5) entsprechend Gleichung (2.9) zu.
1. Maxwellgleichung
r
r
⎛r
∂E ⎞
⎟⇒
rotB = μ ⋅ ⎜⎜ J + ε ⋅
∂t ⎟⎠
⎝
r
r
⎛r
⎞
∂
E
r
⎟⎟
rotB = μ ⋅ ⎜⎜ J + ε ⋅
∂E r
ε << J
∂
t
⎝
⎠
∂t
GL. 2.9
r
r
⇒ rotB = μ ⋅ J
Der Einfluss der partiellen Ableitung der elektrischen Feldstärke ist bei langsamen
Veränderungen sehr gering. Der sogenannte Verschiebungsstrom ist gegenüber der
Leitungsstromdichte vernachlässigbar. Durch diese Vereinfachung ist die erste Maxwell’sche
Gleichung ident mit jener für stationäre Verhältnisse. Man bezeichnet daher niederfrequente
Vorgänge als quasistationär. Für den quasistationären Fall gelten die angeführten
Gleichungen.
Peter Unterwieser
Seite 12
Grundlagen der magnetischen Felder
I.
r
rotB = μ ⋅ J
II.
r
r
∂B
rotE = −
∂t
III.
r ρ
divE =
IV.
r
divB = 0
Ein
stationäres
GL. 2.10
ε
magnetisches
Feld
wird
als
Vektorfeld
durch
Funktionen
der
Aufpunktskoordinaten für die Vektorkomponenten beschrieben. Für zeitveränderliche
Magnetfelder ergibt sich die Zeit als weiterer bestimmender Parameter.
⎛ B x ( x, y , z , t ) ⎞
r
⎜
⎟
B ( x, y , z , t ) = ⎜ B y ( x, y , z , t )⎟
⎜ B ( x, y , z , t ) ⎟
⎝ z
⎠
GL. 2.11
Für den Fall eines quasistationären, periodischen Feldes, ändern sich die Komponenten der
Feldvektoren periodisch.
2.3 Niederfrequente Magnetfelder bzw. ELF-Magnetfelder
Technisch erzeugte magnetische Felder im Bereich der elektrischen Energietechnik sind in
der Regel niederfrequente magnetische 50-Hz- bzw. 16-2/3-Hz-Wechselfelder. Sie werden in
der Folge mit ELF-Magnetfelder (Extremely Low Frequency) bezeichnet. Diese ELFMagnetfelder treten überall auf, wo elektrische Energie transportiert oder umgesetzt und wo
elektrische Betriebsmittel des täglichen Lebens betrieben werden. Elektrische Geräte, die
Strom aus Steckdosen beziehen, jede Leitung der Elektroinstallation in Haushalten, jedes
Kabel, jede Freileitung, jeder Transformator, jede Bahnanlage und jede elektrische Maschine
erzeugen niederfrequente magnetische und elektrische Felder in ihrer Umgebung.
Elektrische Felder sind im Vergleich zu magnetischen Feldern einfach abzuschirmen. Sie
treten in der Umgebung von Bahnanlagen in so kleinem Maße auf, dass hier auf ihre
Untersuchung verzichtet werden kann.
Peter Unterwieser
Seite 13
Grundlagen der magnetischen Felder
2.4 Berechnung magnetischer Felder
Die von stromdurchflossenen Leitern ausgehenden magnetischen Felder werden im Zuge
dieser Arbeit in einem Teilleitermodell durch Polygonzüge nachgebildet, und nach dem BiotSavart’schen Gesetz berechnet. Die Berechnung der magnetischen Ersatzflussdichte erfolgt
nach den in der ÖNORM S1119 festgelegten Berechnungsmethoden.
Als Hilfe für die Berechnung kommt das Programm MF-Calc-railway zum Einsatz. Autor des
Programms ist Dipl.-Ing. Andreas Abart.
2.4.1 Berechnung der Ersatzflussdichte nach ÖNORM S1119
In der ÖNORM S1119 „Niederfrequente elektrische und magnetische Felder - Zulässige
Expositionswerte zum Schutz von Personen im Frequenzbereich von 0...30 kHz“ wird die
Ersatzflussdichte (EFD), als die für die Exposition entscheidende Größe festgelegt. Die
Ersatzflussdichte ist daher als, das Ausmaß der Exposition bestimmende Größe,
heranzuziehen4.
Die Ersatzflussdichte errechnet sich per Definition aus den Vektorkomponenten der
magnetischen Flussdichte laut der Formel.
EFD = Bx2 + B y2 + Bz2
GL. 2.12
EFD … magnetischen Ersatzflussdichte [ μT ]
Bx ... X - Komponente der magnetischen Flussdichte [ μT ]
By ... Y - Komponente der magnetischen Flussdichte [ μT ]
Bz ... Z - Komponente der magnetischen Flussdichte [ μT ]
4
Abart, A.: Visualisierung der 50 Hz Magnetfelder im Haushalt und in öffentlichen Bereichen. TU Graz, Institut
für Elektrische Anlagen.
Peter Unterwieser
Seite 14
Grundlagen der magnetischen Felder
2.5 Grundlagen der Messung von elektromagnetischen Feldern
„Für die Messung von reinen Wechselfeldern ist die Methode der ruhenden Spulen die
einfachste und ohne großen apparativen Aufwand durchzuführen“ (Studie 1997 ÖBM)5 .Viele
Messinstrumente sind für die Analyse magnetischer Felder im Arbeitsbereich sowie im
öffentlichen Bereich konzipiert, mit dem Ziel die Einhaltung oder gegebenenfalls die
Überschreitung der Grenzwertempfehlungen zu dokumentieren. In der Regel zeigen daher
solche Instrumente die Ersatzflussdichte, die nach ÖNORM S1119 die bestimmende, fiktive
Größe ist, mit guter Genauigkeit an.
Die Anforderungen der wissenschaftlichen Analyse liegen jedoch weitaus höher, da hier
neben der Ersatzflussdichte auch die Richtung des Vektors der magnetischen Flussdichte, das
bedeutet die Aufteilung auf die drei räumlichen Komponenten der Flussdichte, von Interesse
ist.
2.5.1 Physikalische Zusammenhänge
Grundlage für die Messung niederfrequenter magnetischer Wechselfelder mit einer Spule ist
das Induktionsgesetz. Als Sensor wird dabei eine Spule mit der Fläche A (Größe und
Richtung) und der Windungszahl N verwendet. Es werden sowohl Spulen mit Ferritkernen,
als auch solche ohne Kern verwendet. Hochpermeable Kerne verursachen eine Verdichtung
des Flusses durch die Spulenfläche und erhöhen so die Empfindlichkeit. Tritt ein zeitlich
veränderlicher magnetischer Fluss durch die Spule, so wird eine ebenso zeitlich veränderliche
Spannung Uind in die Spule induziert.
U ind = − N
dΦ
dt
Φ
... magnetischer Fluss [ Wb ]
N
... Windungszahl der Induktionsspule
Uind
… induzierte Spannung [ V ]
5
GL. 2.13
Kunsch B., Neubauer G., Garn H., Bonek E., Leitgeb N., Magerl G., Jahn O. : Studie dokumentierter
Forschungsresultate über Wirkung elektromagnetischer Felder Teil 1; Bundesministerium für Gesundheit und
Konsumentenschutz, 1997
Peter Unterwieser
Seite 15
Grundlagen der magnetischen Felder
Die Spannung zwischen den Enden einer leerlaufenden Spule ist proportional der zeitlichen
Änderung des von ihr umfassten magnetischen Flusses Φ.
r
Φ = ∫ B ⋅ dA
[Wb]
GL. 2.14
A
Bei zeitlich sinusförmigem Verlauf der mit einer Spule (mit N Windungen) verketteten
v
Flussdichte B(t ) , ergeben sich für den Effektivwert der in der Spule induzierten Spannung die
r
folgenden Gleichungen, wobei n die Richtung der Flächennormalen der Spulenfläche
darstellt.
r
B(t ) = Bˆ ⋅ sin (ωt + ϕ )
0
r r
d ∫ B ⋅ dA
U = −N ⋅
dt
r r
∫ B ⋅ dA ≈ B ⋅ A
(
U = −N ⋅ A⋅
)
d (B0 ⋅ sin (ω ⋅ t + ϕ ))
dt
[T]
GL. 2.15
[V]
GL. 2.16
[ Wb ]
GL. 2.17
[V]
GL. 2.18
[V]
GL. 2.19
r
B
= B cos(ω ⋅ t + ϕ )
eff
0
(
r r
U eff = N ⋅ A ⋅ ω ⋅ BEff ⋅ cos ∠B, n
ϕ
)
... Phasenverschiebung der induzierten Spannung [ 1 ]
Der Zeitverlauf der Spannung entspricht, gemäß den Gleichungen 2.16 bis 2.19, der zeitlichen
Ableitung der Messgröße. Das Amplitudenspektrum des Messsignals ist gegenüber jenem der
Messgröße proportional der Frequenz ansteigend. Das Phasenspektrum bleibt unverändert.
Die Dimensionierung der Sensorspule ist so zu wählen, dass sich ein günstiger
Proportionalitätsfaktor zwischen der Flussdichte und der an der Spule abgegriffenen
Spannung ergibt (z.B. die Größe der Spule ist insbesondere bei der Messung von Feldern, die
in Relation zu den Spulenabmessungen inhomogen sind, von Bedeutung. Die von der
deutschen Norm DIN 848 geforderte 100 cm² - Spulenfläche wird von kleinen
Handmessgeräten meist nicht erfüllt. Durch Variation der Spulenrichtung in einem Aufpunkt
des Feldes kann im Wechselfeld der maximale Wert der induzierten Spannung gemessen
werden. Die Flächennormale gibt dann die Richtung an (Abbildung 2.4). Diese Ausführungen
gelten unter der Voraussetzung eines im Bereich der Spule homogenen Feldes.
Peter Unterwieser
Seite 16
Grundlagen der magnetischen Felder
Abbildung 2.4 : Messprinzip für die mag. Flussdichte unter Berücksichtigung der
r r
r
r
Neigung α = ∠B, n der Spulen- (n ) zur Feldachse B
(
)
()
2.5.2 Messverstärker
Der in Kapitel 2.5.1 beschriebene Frequenzgang der Messwertumformung kann durch ein
aktives oder passives Glied kompensiert werden. Als aktives Glied wird meist ein Integrator
verwendet werden. Darüber hinaus sollte ein Bandpassverhalten höherer Ordnung für die
Unterdrückung der Bewegungsinduktion im Erdmagnetfeld und die Begrenzung auf den ELFBereich sorgen. Manche Sonden sind auch mit Selektivfiltern ausgestattet um beispielsweise
bahnfrequente Felder von 50-Hz-Feldern unterscheiden zu können. Der Messbereich der ELFMF-Sonden zur Expositionsmessung überspannt je nach Destination meist mehrere
Zehnerpotenzen (2 oder 10 nT ... 5 mT manche auch darüber). Bei digitalen Instrumenten
weist der Messverstärker meist logarithmische Übertragungseigenschaften auf.
2.5.3 Messung zeitvarianter magnetischer Felder
Von zeitvarianten Feldern spricht man, wenn sich die Flussdichte für jeden Zeitaugenblick
ändert. Wenn man jedoch ein Profil der magnetischen Flussdichte mit nur einer Messsonde
messen will, setzt man voraus, dass sich das magnetische Feld zeitlich nicht ändert. Während
der Aufnahme eines Profils der magnetischen Flussdichte einer Bahnanlage, einer
Hochspannungsleitung oder von PEN-Leitern, bleibt der Belastungszustand der Leiter und
damit die gemessenen Flussdichten in verschiedenen Raumpunkten nicht konstant. Es ändert
Peter Unterwieser
Seite 17
Grundlagen der magnetischen Felder
sich in der Regel der feldverursachende Strom während in den einzelnen Aufpunkten
gemessen wird. Das führt dazu, dass das gemessene quasistationäre Profil von den zeitlichen
Feldänderungen, verursacht durch die Lastflusssituation, überlagert wird.
Zur Elimination der zeitlichen Änderungen benötigt man eine zweite Messsonde, die während
der gesamten Messung die zeitliche Varianz in einem Aufpunkt misst. Diese Sonde wird als
stationäre Sonde bezeichnet. Die erste Sonde wird als mobile Sonde bezeichnet und wird
entlang der Aufpunktsgeraden an den einzelnen Messpunkten positioniert. Wird nun die von
der mobilen Sonde gemessene Flussdichte auf die der stationären Sonde bezogen, so lässt sich
die Zeitvarianz des Feldes eliminieren. Diese zeitlich korrigierte Messreihe entspricht einer
Messreihe bei der alle Messpunkte zum gleichen Zeitpunkt t0 aufgenommen werden.
xbez. ( x, t 0 ) =
X mob ( x, t )
Bstat ( x0 , t )
[1]
GL. 2.20
xbez(x,t0) … bezogene Vektorkomponenten der charakteristischen Verteilung für den
Zeitpunkt t0
Xmob(x,t) … gemessene Vektorkomponenten am Ort x zur Zeit t [ μT ]
Bstat(x0,t) … gemessene EFD der stationären Sonde zur Zeit t [ μT ]
Um ein physikalisches Ergebnis mit der Einheit μT zu erhalten wird die Gleichung 2.20 noch
mit dem Wert der mobilen Sonde multipliziert6.
B X _ MOB _ korr ( x, t 0 ) =
BX _ MOB ( x, t )
BEFD _ STAT ( x0 , t )
⋅ BEFD _ MOB ( x0 , t0 )
[μT]
GL. 2.21
Die Zusammensetzung der Ersatzflussdichte aus den einzelnen Komponenten sieht man in
Abschnitt 2.4.1.
EFD = B X2 + BY2 + BZ2
6
[μT]
GL. 2.22
Diplomarbeit. TU Graz, Institut für Elektrische Anlagen. 1997.Andreas Abart
Peter Unterwieser
Seite 18
Grundlagen der magnetischen Felder
Bei diesem Verfahren wird vorausgesetzt, dass das Zeitverhalten im Aufpunkt der stationären
Sonde, jenem in den Aufpunkten der mobilen Sonde entspricht. Gleichzeitig darf sich die
räumliche Verteilung auch nicht ändern.
Durch die Aufnahme mehrerer Messpunkte entlang einer Achse erhält man ein Profil. Dieses
Profil gibt die räumliche Verteilung des Magnetfeldes wieder.
2.5.3.1 Verwendete Messgeräte
Combinova-FD3
Das FD3 ist ein kompaktes Messgerät, das speziell zur Messung niederfrequenter
magnetischer Felder konzipiert wurde. Durch drei im Gerät orthogonal angeordnete Spulen
erfasst der Datenlogger die kartesischen Vektorkomponenten der magnetischen Flussdichte
gleichzeitig und zeichnet die Messwerte auf. Das Messgerät wird als stationäre Sonde
eingesetzt, weil es automatisch Messwerte in vorgegeben Zeitintervallen aufnimmt und
speichert.
Abbildung 2.5 : Combinova-FD3 mit Skizze der Spulenachsen
Peter Unterwieser
Seite 19
Grundlagen der magnetischen Felder
Die Bedienung ist sehr einfach. Ähnlich wie bei einem Videorecorder können bei der
Programmierung durch die Software unter Windows die Beginn- und Endzeiten für die
Messung
festgelegt
werden.
Auch
tägliche
Aufzeichnungen
während
bestimmter
Zeitintervalle sind möglich. Im manuellen Modus kann die Messung durch Drücken der
Tasten
gestartet
beziehungsweise
gestoppt
werden.
Wahlweise
werden
die
Sekundenmittelwerte für den Betrag oder jene der einzelnen Komponenten in Intervallen von
1 bis 600 Sekunden aufgezeichnet.
Spezifikationen der Sonde:7
• Drei orthogonal ausgerichtete Spulen
• Frequenzbereich 20 Hz bis 2000 Hz - (ELF Extremly Low Frequency)
• großer Dynamikumfang 10nT - 100 µT
• wahlweise Betragsmessung oder Komponentenmessung
• LED-Balkenanzeige
• Speicher für 60.000 Messwerte - serielle Schnittstelle zur Datenübertragung
• Stromversorgung durch zwei R6 (AA) 1,5 Volt Batterien
• Lederetui mit Spange zur Befestigung am Hüftgurt
In den Spezifikationen wird der Frequenzbereich mit 20-2000 Hz angegeben. Die OEBB
verwenden für die Energieversorgung ein Wechselspannungsnetz mit 16 2/3 Hz. Deshalb
entstehen in der Umgebung von Bahnanlagen Wechselfelder mit 16 2/3 Hz. Um 16 2/3 Hz zu
messen ist der Messwert der EFD mit 2 zu multiplizieren. Dieser Faktor wird bestimmt durch
den Frequenzfilter des Messgerätes und ist dem Manual zu entnehmen.
Weiters ist das Combinova-FD3 nicht im Stande frequenzselektiv zu messen. Eine
Feldkomponente in einer Richtung ist somit die Summe aller Feldkomponenten in dieser
Richtung für die verschiedenen Frequenzen des betrachteten Freuqenzbandes. Aus den drei
gemessen Komponenten wird die EFD errechnet. Als Kontrolle ist es üblich, zuerst
frequenzselektiv zu messen, um so die Komponenten der einzelnen Frequenzen abzuschätzen.
Tragen die Felder mit 16 2/3 Hz den größten Teil zur Summe bei, ist der Fehler bei nicht
frequenzselektiver Messung vernachlässigbar klein. Eine frequenzselektive Messung kann z.
B. mit dem EM-Feldanalysator EFA-3 durchgeführt werden.
Da die OEBB als Netzfrequenz 16 2/3 Hz, das allgemeine Energieversorgungsnetz aber 50 Hz
verwendet, ist eine eindeutige Zuordnung der magnetischen Felder über deren Frequenz
7
Bedienungsanleitung Combinova-FD3
Peter Unterwieser
Seite 20
Grundlagen der magnetischen Felder
möglich. Das heißt alle Felder mit 50 Hz stammen ursprünglich von dem allgemeinen
Energieversorgungsnetz. Alle Felder mit 16 2/3 Hz können nur von der OEBB verursacht
werden.
Das Messgerät kann mittels Rechner ausgelesen werden. Das Combinova-FD3 wird bei den
folgenden Messungen als ortsfeste Messsonde eingesetzt.
EM-Feldanalysator EFA-3 von Wandel & Goltermann
Das Messgerät EFA-3 ist für die Messung elektrischer und magnetischer Felder geeignet. Es
erfasst die drei Vektorkomponenten der magnetischen Flussdichte. Es ist eine
frequenzselektive oder eine bandselektive Messung möglich. Somit ist es möglich, nur
magnetische Felder der Frequenz 16 2/3 Hz zu messen. Das Messgerät verfügt über eine
interne Magnetfeldsonde. Die interne Sonde ermöglicht es mit geringem Aufwand Felder
festzustellen und zu messen. Trotz der kleinen Abmessungen beträgt der Messfehler der
Messung noch ca. 6 %. Außerdem kann eine externe Präzisions-B-Feld-Sonde angeschlossen
werden. Die externe Präzisions-B-Feld-Sonde verfügt über Messspulen mit 100 cm2
Querschnittsfläche. Die VDE-Norm 0848 schreibt eine Sonde mit einer wirksamen
Querschnittsfläche von 100 cm2 vor. Durch die große Fläche ergibt sich eine gute
Fehlerklasse von ca. 3 %. Diese Sonde ist auch vorteilhaft, um bei Messungen die Wirkung
kleiner Wirbelfelder auszuschließen
Die folgenden Angaben sind der Bedienungsanleitung8 des Messgerätes entnommen.
Frequenzbereich:
5 Hz...30 kHz (3 dB)
Messbereich:
100 nT, 1 μT, 10 μT, 100 μT, 1 mT, 10 mT
automatische Messbereichswahl möglich
Frequenzmessung (bei Breitbandmessung)
Frequenzanzeige:
1 Hz...30 kHz
Auflösung:
1 Hz
8
Bedienungsanleitung EFA-1/EFA-2/EFA-3EM-Feldanalysator B-Feld, BN 2245/98.01
Peter Unterwieser
Seite 21
Grundlagen der magnetischen Felder
Filterfunktionen:
Breitbandmessung:
5 Hz...2 kHz, 30 Hz...2 kHz
5 Hz...30 kHz, 30 Hz...30 kHz
Selektivfilter:
16,7 Hz, 33,3 Hz, 50 Hz, 60 Hz
100 Hz, 120 Hz, 150 Hz, 180 Hz
400 Hz, 800 Hz, 1200 Hz
Variable Filter (EFA-2/-3):
von 15 Hz ...2 kHz
Messgenauigkeit: EFA mit externer B-Feld-Präzisionssonde (100 cm2 Fläche)
Allgemeine Daten:
Anzeigeauflösung :
0,1 %
Auffrischrate der Anzeige:
ca. 3/s
Messbereichswahl:
manuell
Alarmfunktionen:
Schwelle einstellbar und ein/aus
Abmessungen (B x H x T in mm):
ca. 110 x 200 x 60
Gewicht (inkl. Akkus):
ca. 1 kg
Selbsttests:
Automatischer Selbsttest nach dem Einschalten: Warnfunktionen, Wandlertest, Speichertest,
Prüfung der Betriebsspannung.
Das Messgerät wird als mobile Sonde eingesetzt. Es speichert markierte Messwerte mit. Das
Messgerät kann mittels Rechner ausgelesen werden.
Peter Unterwieser
Seite 22
Grundlagen der magnetischen Felder
Abbildung 2.6 : Achsen und Frontansicht des Magnetfeldmessgerätes EFA-3
2.6 Prinzip und Problematik der verteilten Rückleitung
Bei der Berechnung von magnetischen Feldern ist zu berücksichtigen, dass es sich in der
Regel nicht um einzelne Leiter in abgeschlossenen Systemen handelt. Meist sind es mehrere
Leiterschleifen, die miteinander kapazitiv und induktiv gekoppelt sind. Sie beeinflussen sich
daher gegenseitig. Bei Leiterschleifen sind Längs- und Querimpedanzen zu berücksichtigen.
Bei der Rückleitung eines Wechselstroms im Erdreich bildet sich zwischen den
Erdungspunkten ein Strömungsfeld aus, das von der Leitungsführung beeinflusst wird. Der
Rückstrom im Erdreich wird durch die Wirkung des magnetischen Feldes unter der Leitung
gebündelt und folgt der Leitungsführung. Im Erdreich ergibt sich dabei eine bestimmte
Stromdichteverteilung.
Erklärung der verteilten Rückleitung anhand des Beispieles Bahnanlage:
Sowohl die Zuleitungen als auch die Rückleitungen einer Bahnanlage bestehen aus mehreren
Leitern. Die Zuleitungen sind das Tragseil, der Fahrdraht und Unterstützungsleitungen. Die
Rückleiter bilden die Schienen, das Erdreich und alle mit dem Erdungssystem verbundenen
parallelen Rückleiter. Dies können auch die Armierungsleiter eines Tunnels sein. In all diesen
Peter Unterwieser
Seite 23
Grundlagen der magnetischen Felder
Leitern fließen Ströme, die sich entsprechend der Impedanzen aufteilen. Jeder dieser Ströme
bildet ein magnetisches Feld aus, dessen Richtung von der Stromrichtung, und dessen
Amplitude von der Größe des verursachenden Stromes abhängt. All diese Felder überlagern
sich nun zu einem resultierenden Feld, welches einen sehr komplexen räumlichen Verlauf
annehmen kann.
Die Summe all dieser Einflussfaktoren stellt die große Komplexität bei der Messung und
Berechnung magnetischer Felder in Systemen mit verteilter Rückleitung dar.
2.7 Grenzwerte
Die zulässigen Grenzwerte für magnetische und elektrische Felder sind in der ÖNORM S
1119 festgelegt. Sie werden dort definiert als Exposition der Allgemeinbevölkerung durch
zeitlich veränderliche elektrische und magnetische Felder. Sie stimmen mit den Richtlinien
der ICNIRP (internationale Kommission zum Schutz vor nichtionisierender Strahlung)
überein und sind von der WHO (world health organisation) anerkannt.
Die zulässige Höhe der Grenzwerte hängt von der Frequenz des Feldes ab.
Frequenz [Hz]
16 2/3
50
elektrisches Feld [kV/m] magnetische Ersatzflussdichte [µT]
10
300
5
100
Tabelle 2.1 : Grenzwerte für magnetische und elektrische Felder
Die Grenzwerte der magnetischen Ersatzflussdichte werden in den hier durchgeführten
Simulationen bei weitem nicht erreicht. Deshalb ist es nicht nötig Reduktionsleiter aufgrund
einer Grenzwertüberschreitung anzuordnen.
Peter Unterwieser
Seite 24
Programmierung
3 Programmierung
Ein wichtiger Teil der Diplomarbeit beschäftigt sich mit der Berechnung und Darstellung von
magnetischen Feldern. Dazu wurde das Softwarepaket MF-Calc-railway vom Institut für
Elektrische Anlagen der TU Graz verwendet. Der Autor dieses Programms ist Dipl.-Ing.
Andreas Abart.
3.1 Wie arbeitet MF-Calc-railway?9
•
Einfache, effiziente dialoggeführte Eingabe von Bahnanlagen als ebene Probleme
•
Berechnung der Stromverteilung in Leiteranordnungen mit Hilfe der Koppelimpedanzen (abhängig von Material und Geometrie) unter dem Einfluss erdfühliger
Rückleiter
•
Berechnung der magnetischen EFD als Verteilung in vertikalen Schnittebenen oder
über horizontalen Aufpunktgeraden nach Biot-Savart
Die Berechnung ebener Probleme ist in der Praxis der EMF-Bewertung oft von Vorteil. Durch
die Modellreduktion in eine (Schnitt-) Ebene werden die Aufwände für die Modellierung
ebenso wie für die Berechnung erheblich reduziert. Abweichungen des Modells von den
realen Bedingungen sind für 3D-Modelle ebenso gegeben, wie bei ebenen 2D-Modellen, da
oft Details der Erdungsanlage bzw. darin eingebundener Leitungssysteme völlig unklar sind.
Es sei an dieser Stelle darauf hingewiesen, dass für den Nachweis der tatsächlichen EMFExposition ein aus Rechnung und Messung bestehendes Analyseverfahren am besten geeignet
ist.
Die Leiter einer im Modell unendlich langen Energieleitung sind je Längeneinheit durch
Koppelimpedanzen
verbunden.
Es
ergibt
sich
eine
Ersatzschaltung
über
deren
Knotenadmittanzmatrix die Stromverteilung berechnet wird. Die Koeffizienten entsprechen
den Koppeladmittanzen, die sich aus Leiterposition, Leiterdicke, Materialkonstanten und
Widerstandsbelag ergeben.
Das magnetische Feld in der Umgebung des einzelnen, geraden, unendlich langen Leiters
wird nach den Gleichungen, die sich aus dem Satz von Biot-Savart ergeben, berechnet. Dabei
9
Abart, A.: Auszüge aus Programmbeschreibung und Bedienungsanleitung MF-Calc-railway. TU Graz, Institut
für Elektrische Anlagen.
Peter Unterwieser
Seite 25
Programmierung
wird der Leiter fadenförmig angenommen und weder eine Stromverteilung im Inneren des
Leiters, noch seine magnetischen Eigenschaften berücksichtigt. Diese Einflüsse sind
hinsichtlich der ohnedies bestehenden Unschärfe in der Modellbildung vernachlässigbar.
Die Aufgabe in dieser Diplomarbeit bestand nun darin, die Ersatzflussdichte inner- und
außerhalb eines Tunnels zu berechnen. Um einen Tunnel simulieren zu können, musste das
dazu verwendete Tunnelmodul erst in das Programm implementiert werden.
3.2 Formelwerk zu MF-Calc-railway
Ein genaues Formelwerk zu MF-Calc-railway in englischer Sprache ist im Anhang
ersichtlich. Unter dem Titel “MF-Calc-Railway –The formula base” verfassten Dipl.-Ing.
Andreas Abart und Dr. Ernst Schmautzer eine Beschreibung der mathematischen
Hintergründe.
3.3 Grundsätzliche Überlegungen zur Tunnelsimulation
Ein Eisenbahntunnel wird heute in Beton- oder Stahlbetonbauweise ausgeführt. Wenn keine
erhöhten Anforderungen an die Festigkeit gestellt werden, wird die Betonbauweise
verwendet. Diese kann kostengünstiger realisiert werden, hat aber den Nachteil, dass aufgrund
der fehlenden elektrischen Armierungsleiter das magnetische Feld nicht beeinflusst werden
kann. Tunnelbauwerke älterer Bauart sind meist in Betonbauweise ausgeführt.
Der Stahl im Beton führt zu einer erhöhten Festigkeit des Werkstoffgemisches. Er nimmt
dabei die Zugkräfte auf. Der Stahl kann Zugkräfte besser beherrschen als Beton. Der Beton
leitet die Druckkräfte ideal ab. Deshalb ist die Kombination aus Stahl und Beton ein idealer
Werkstoff für alle Arten von Belastungszuständen. Beide Werkstoffe haben einen ähnlichen
Temperaturkoeffizienten, d.h. sie dehnen sich bei Temperaturänderungen gleichmäßig aus
ohne Sprünge im Material zu bilden. Diese gleichmäßige Ausdehnung ist die Voraussetzung
für eine lange Lebensdauer. Somit ergibt sich ein idealer Verbundwerkstoff aus
bautechnischer Sicht.
Bei Herstellung wird zuerst das Stahlgerüst aufgebaut, dabei werden die Stahlstangen,
Stahlbögen und ähnliche Stahlteile miteinander verbunden. Dieses Gerüst wird anschließend
mit flüssigem Beton ausgegossen bzw. gespritzt. Am Ende ist der Stahl vollkommen im
Peter Unterwieser
Seite 26
Programmierung
Werkstoff Stahlbeton integriert. Einzig die Erdungsbänder der Stahlteile sind nach außen
geführt. Diese Stahlbänder werden nun miteinander und mit der Erdungsanlage verbunden.
Die Stahlstangen im Stahlbeton und die Erdungsbänder sind die Voraussetzung für die
Leitung eines elektrischen Stromes. Mit elektrischem Strom sind hier die induzierten Ströme
und Rückströme der Energieübertragung gemeint.
Im Folgenden gilt es zu untersuchen, wie oft der Stahl im Beton untereinander und mit der
Erdungsanlage zu verbinden ist, um möglichst gute Reduktionswirkungen zu erzielen.
Die Vorrausetzung für die Gültigkeit, der in dieser Diplomarbeit durchgeführten
Simulationen, sind Stahlleiter im Beton, d. h. Stahlbetonbauweise.
Physikalisch führen die Armierungsleiter und alle anderen Rückleiter den Rückstrom des
Triebfahrzeuges. Der Strom teilt sich entsprechend der Impedanzen auf. Außerdem werden
über das magnetische Feld Ströme in die Armierungsleiter induziert. Diese Ströme fließen in
entgegengesetzter Richtung zu den Traktionsströmen. Die Rückleiterströme und die
induzierten Ströme bilden in Summe ein magnetisches Feld aus, welches entgegen dem
verursachenden Feld wirkt. Deshalb verstärken sie das Feld innerhalb des Tunnels und
schwächen es außerhalb des Tunnels ab. Diese Feldreduzierung in Abhängigkeit der
Erdungssituation des Tunnelbauwerkes gilt es zu untersuchen. Die Erdung gibt Auskunft
darüber, wie gut diese Leiter miteinander und mit der Erde verbunden sind. Je besser die
Verbindung der Leiter in den einzelnen Abschnitten und die mit der Erde ist, desto mehr
Rückströme werden sie führen und desto besser ist die Reduktionswirkung. Mit Verbindung
der einzelnen Tunnelabschnitte sind die elektrischen Verbindungen der Blockfuge gemeint.
Peter Unterwieser
Seite 27
Programmierung
Es soll nun kurz die Bedeutung der Symbole in nachfolgenden Abbildungen erklärt werden.
1
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
> 500
< 500
< 400
< 300
< 200
< 100
< 50
< 40
< 30
< 20
< 10
< 5
< 4
< 3
< 2
< 1
< 0.5
< 0.4
< 0.3
< 0.2
< 0.1
< 0.05
< 0.04
< 0.03
< 0.02
< 0.01
< 0.005
< 0.004
< 0.003
< 0.002
< 0.001
2
2
12,0
3
11,0
10,0
10
10
3
9,0
8,0
Y
7,0
6,0
20
3,0
1
30
4,0
5
1
20
0.5
2
10
30
5,0
1,0
2
10
3
2,0
1
-1,0
5
0.4
0.5
5
0,0
X
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
TU-Graz
A.Abart 2003
Abbildung 3.1 : Magnetische EFD einer zweigleisigen Bahnanlage unter Einfluss eines
Tunnels
Alle Leiter der Bahnanlage sind als rote Symbole dargestellt. Die Oberleitungen sind als rote
Rechtecke, die Schienen als rote Gleisprofile und die Armierungsleiter als grüne Punkte
abgebildet. Die blauen Bereiche stellen die Größe des Feldes der EFD dar. Unten ist die X
Achse, und rechts die Y Achse in Metern aufgetragen. Die hellgrauen Kästchen mit der Linie
auf die Oberleitungen (rote Rechtecke) sind Objektbezeichner. Die Zahlen in den hellgrauen
Kästchen geben den Wert der EFD wieder.
Der Tunnel wird durch eine geometrische Anordnung von unendlich langen erdfühlig
verlegten Leitern nachgebildet. Diese Leiter werden vom Programm als Rückleiter gesehen,
d.h. sie führen Rückströme. Die Rückströme verteilen sich entsprechend ihrer Impedanzen.
Die Koppelimpedanzen der Leiter berücksichtigen die Ströme, die über das magnetische Feld
eingekoppelt werden.
Peter Unterwieser
Seite 28
µT
13,0
Programmierung
Das Tunnelmodul besteht aus drei Teilen. Das Erste ist für die Eingabe des Tunnels
zuständig.
Mit
der
Schaltfläche
„Tunnel
hinzufügen“
kommt
man
in
das
Tunnelbearbeitungsmodul. Dort betätigt man in der linken oberen Ecke den grau dargestellten
Tunnelleiter. Es erscheint ein neuer grüner Tunnelleiter der ausgewählt werden kann. Die
einzelnen Leiterstäbe können mittels „drag and drop“ an der gewünschten Stelle positioniert
werden. Pro Tunnel können bis zu 45 Leiter verwendet werden. Weiters besteht die
Möglichkeit der Eingabe mittels Tabelle. Die Tabelleneingabe hat den Vorteil die Geometrie
genauer nachbilden zu können. Eine zentimetergenaue Eingabe der Maße des Tunnels und der
Position der Leiter ist nur in der Tabellenform möglich.
Abbildung 3.2 : Eingabeoberfläche des Tunnels aus MF-Calc-railway
Peter Unterwieser
Seite 29
Programmierung
Nach der Eingabe der Geometrie drückt man auf die Taste „OK“ und beendet so die
Leiterpositionierung. Dann werden die charakteristischen Parameter eingeben. Dies sind der
Leiterdurchmesser und den Widerstandsbelag in Ω/km. Die realen Stäbe im Stahlbeton sind
sehr klein und in sehr großer Anzahl vorhanden, deshalb wird in der Simulation der Tunnel
mit weniger Stäben in größeren Abständen nachgebildet. Welchen Durchmesser und Abstand
sie haben sollten um eine gute Übereinstimmung mit der realen Situation zu erhalten, gilt es
in dieser Arbeit erst zu klären. Ein realer Durchschnittswert ist 26,8 cm2 Stahl im m2 Beton.
Er stammt aus dem aktuellen Bauvorhaben der Koralmbahn Nähe Graz.
Abbildung 3.3 : Eingabeoberfläche des Tunnels für die charakteristischen Daten
Peter Unterwieser
Seite 30
Programmierung
Der zweite Teil ist für die grafische Darstellung zuständig. In diesem Teil können die Leiter
in einem Bearbeitungsmodus nachträglich verschoben, erweitert oder gelöscht werden. Hier
wurde besonderes Augenmerk auf die Einfachheit und Übersichtlichkeit gelegt.
Abbildung 3.4 : Änderungsoberfläche des Tunnelmoduls aus MF-Calc-railway
Peter Unterwieser
Seite 31
Programmierung
Der dritte Teil ist zuständig für die Berechnung. Man wählt „Berechnen“ aus, kommt dann
zum Darstellungsfenster, wählt dort die gewünschte Darstellung aus und erhält nach kurzen
Berechnungen das Ergebnis.
Abbildung 3.5 : MF-Calc-railway beim Berechnungsvorgang
Peter Unterwieser
Seite 32
Programmierung
Der vierte Teil beschäftigt sich mit der Visualisierung der Ergebnisse. Das magnetische Feld
kann als Feldplot ausgegeben werden. Hier wird der gesamte Bereich in Falschfarben
entsprechend der Werte der EFD dargestellt. Als zweite Möglichkeit gibt es die Darstellung
als Profil, bei welcher die gewünschte Schnittebene frei gewählt werden kann. Hier sind die
konkreten Werte der magnetischen Ersatzflußdichte sehr übersichtlich abzulesen.
Abbildung 3.6 : MF-Calc-railway mit dem Berechnungsergebnis
Weiters gibt es eine Darstellung als RESULT Tabelle, die für die weitere Verarbeitungen
ideal geeignet ist. Eine mögliche weitere Verarbeitung wäre es z. B. die Differenz zweier
Feldbilder auszurechnen und darzustellen. Dies ist im Abschnitt 6 dieser Diplomarbeit zu
sehen. Die Ergebnisse werden auch als Matrix in Abhängigkeit ihrer Position in der Ebene
dargestellt.
Die
Implementierung
des
Tunnelmoduls
in
MF-Calc-railway
wurde
mit
der
Programmiersprache „Visual Basic for Application“, die ein Teil von Microsoft Windows ist,
im Zuge der Diplomarbeit realisiert.
Peter Unterwieser
Seite 33
Rechenbeispiel zu MF-Calc-railway
4 Rechenbeispiel zu MF-Calc-railway
4.1 Allgemeines
Anhand eines kurzen Rechenbeispieles wird das magnetische Feld zweier Leiter zuerst
analytisch errechnet. Dann wird die gleiche Anordnung mit MF-Calc-railway gerechnet.
Abschließend wird das Ergebnis mit jenem von MF-Calc-railway verglichen. Dies dient
einerseits zur Erklärung des Rechenprinzips und andererseits zur Kontrolle der mit MF-Calcrailway errechneten Werte.
Gefragt ist die Ersatzflussdichte im Aufpunkt A, die durch zwei stromdurchflossene Leiter
verursacht wird. Der Leiter 1 mit einem Strom von 150 A und der Leiter 2 mit einem Strom
von 250 A.
4.2 Analytischer Rechenvorgang
Ausgangspunkt ist das Biot-Savart’sche Gesetz in differenzieller Form (siehe Gleichung 2.2).
(
r
r μ 0 ⋅ I ⋅ dl × rr
dB =
4π ⋅ r 3
r μ ⋅I 1
dB = 0 ⋅ 2
4π ⋅ r
)
GL. 4.1
r
⎛ r r⎞
d
l
×
⎜
⎟
r⎠
⎝
r r
r r r
er = = r → Einheitsvektor
r r
(
r
r
ds = dl → Linienelement
r μ ⋅I 1 r r
dB = 0 ⋅ 2 dl × er
4π ⋅ r
)
r
r r
I
B = μ⋅∫
⋅ ds × er
2
4πr
s
r μ 0 ⋅ I dsr × rr
B=
4π ∫s r 3
Peter Unterwieser
GL. 4.2
Seite 34
Rechenbeispiel zu MF-Calc-railway
Für einen unendlich langen Leiter in Z Richtung gilt:
r μ ⋅I
B= 0
4π
r r
ds × r
∫ r3
−∞
+∞
⎛ x⎞
r ⎜ ⎟
r = ⎜ y⎟
⎜z⎟
⎝ ⎠
GL. 4.3
⎛0⎞
r ⎜ ⎟
ds = ⎜ 0 ⎟
⎜ dz ⎟
⎝ ⎠
⎛ 0 ⎞ ⎛ x⎞
r r ⎜ ⎟ ⎜ ⎟
r
r
ds × r = ⎜ 0 ⎟ × ⎜ y ⎟ = − y ⋅ dz ⋅ ex + x ⋅ dz ⋅ e y
⎜ dz ⎟ ⎜ z ⎟
⎝ ⎠ ⎝ ⎠
(
r = x2 + y 2 + z 2 ⇒ r 3 = x2 + y2 + z 2
r μ ⋅I
⇒B= 0
4π
r μ ⋅I
B= 0
4π
+∞
∫
−∞
+∞
∫
r
r
x ⋅ e y − y ⋅ ex
r3
−∞
r
r
x ⋅ e y − y ⋅ ex
(x
2
+ y2 + z2
)
3
)
3
2
⋅ dz
⋅ dz =
2
+∞
1
⎛ μ0 ⋅ I ⋅ x r μ0 ⋅ I ⋅ y r ⎞
⋅ ey −
⋅ ex ⎟ ⋅ ∫
⎜
4π
⎝ 4π
⎠ −∞ x 2 + y 2 + z 2
(
+∞
Gesucht ist das Integral
∫
−∞
(x
1
2
+ y2 + z2
)
3
z = +∞
∫
z = −∞
=
(c
1
2
+ z2
)
3
dz
3
dz ⇒
2
dz
2
Substitution: x 2 + y 2 + z 2 = c 2 + z 2
⇒
)
da x und y konstant bezüglich dz sind
laut Formelsammlung
2
z
⋅ c2 + z2
c2
−∞
+∞
=
2
c2
2
x + y2
2
r
r
μ ⋅I
y r μ0 ⋅ I
x
B=− 0 ⋅ 2
e +
e
⋅ 2
2 x
2 y
2π x + y
2π x + y
Peter Unterwieser
GL. 4.4
Seite 35
Rechenbeispiel zu MF-Calc-railway
Für die Komponenten in X und Y Richtung gilt:
Bx = −
By = +
μ0 ⋅ I ⋅ y
(
2π ⋅ x 2 + y 2
μ0 ⋅ I ⋅ x
(
2π ⋅ x 2 + y 2
)
GL. 4.5
)
GL. 4.6
Abbildung 4.1 : Anordnung der Leiter und des Aufpunkts
Abbildung 4.2 : Abstände der Leiter mit Bemaßung
Peter Unterwieser
Seite 36
Rechenbeispiel zu MF-Calc-railway
Zuerst errechnet man die Komponenten der Feldstärken Bx1 und By1 des ersten Leiters.
Abbildung 4.3 : Feldbild der Leiters 1
Es ergibt sich laut Gleichung 4.5:
Bx1 = −
μ0 ⋅ I ⋅ y
2π ⋅ (x 2 + y 2 )
=−
4π ⋅ 10 −7 Vs / Am ⋅ 150 A ⋅ (1m )
2π ⋅ (5m 2 + 1m 2 )
Bx1 = −1,1538μT
Analog errechnet sich die Y Komponente laut Gleichung 4.6:
B y1 =
μ0 ⋅ I ⋅ x
2π ⋅ (x 2 + y 2 )
=
4π ⋅ 10 −7 Vs / Am ⋅ 150 A ⋅ (5m )
2π ⋅ (5m 2 + 1m 2 )
B y1 = 5,7692μT
Peter Unterwieser
Seite 37
Rechenbeispiel zu MF-Calc-railway
Die Komponenten der Feldstärke Bx2 und By2 des zweiten Leiters errechnen sich als:
Abbildung 4.4 : Feldbild der Leiters 2
Bx 2 = 8,7692μT
B y 2 = −3,4483μT
Peter Unterwieser
Seite 38
Rechenbeispiel zu MF-Calc-railway
Die Komponenten der Feldstärke in jeder Achse werden addiert.
Abbildung 4.5 : Feldsuperposition für die Leiter 1 und 2
Bx = Bx1 + Bx 2 = 7,4669μT
B y = B y1 + B y 2 = 2,3205μT
Als Ersatzflußdichte ergibt sich dann laut Abschnitt 2.4.1:
EFD = B x2 + B y2 = 7,8192μT
Peter Unterwieser
Seite 39
Rechenbeispiel zu MF-Calc-railway
4.3 Berechnung mit MF-Calc-railway
Im Reportblatt sieht man alle wichtigen Daten. Ersichtlich sind die eingegeben Daten wie die
Position der Leiter, Leiterdurchmesser, Leiterwiderstand, Strom im Leiter. Weiters alle
errechneten Daten wie die Aufteilung der Ströme in den Rückleitern. In diesem Fall ist das
nur die Erde, in der die Summe aus dem Leiter 1 und dem Leiter 2 zurückfließt. Das sind
400 A mit einem Phasenwinkel von -180º.
Nennspannung
15000 V
Bodenleitfähigkeit
Strom im Erdreich
400
mm²
mm²
m/ Ωmm²
Ω/km
mm
*
*
*
*
*
*
*
*
*
*
Beeinflusste Leitung 3
Beeinflusste Leitung 2
Beeinflusste Leitung 1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
15000 *
*
*
*
*
*
*
*
*
*
*
*
*
*
Beeinflusste Leitung 3
*
*
*
*
*
Beeinflusste Leitung 2
Beeinflusste Leitung 1
Rückleitung 3
Rückleitung 2
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
95 *
*
*
0,195 *
11,00087 *
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
-
*
*
*
*
*
-
0 *
*
*
250,00
0,00
*
*
*
*
*
*
*
*
*
*
-
*
*
*
*
*
*
*
*
*
*
*
*
-
*
*
*
*
*
*
*
*
*
*
*
*
*
-
*
2*
5*
*
*
*
*
*
Rückleitung 1
*
*
*
*
*
*
*
-
*
*
95 *
*
*
0,195 *
11,00087 *
*
*
Hilfsleitung 3
*
*
*
*
*
-
Cu95
-
*
*
*
*
*
-
0 *
*
*
150,00
0,00
*
*
-
*
-
*
*
-
*
*
*
*
*
Rückleitung 3
*
-
*
*
*
Mast
*
*
*
*
*
Rückleitung 2
*
*
*
-
*
*
*
-
*
*
*
*
*
*
*
*
Rückleitung 1
*
*
*
-
*
*
*
Hilfsleitung 2
*
*
*
*
*
*
*
*
Hilfsleitung 3
*
*
15000 *
-
-5 *
-1 *
*
-
*
*
*
*
*
-
Materialbezeichnung
Querschnitt 1
Querschnitt 2
spez. Leitfähigkeit
Widerstandsbelag
äquiv. Durchmesser
0*
0*
*
*
*
*
*
*
-
Profiltyp:
X/m
standard1
Y/m
Trak tionsstrom It/A
U/V *
250
U/° *
0 deltaU/V *
Nennspannung
deltaU/° *
15000
I/A *
0
I/° *
Horizontalwinkel
0°
*
*
*
-
GR2
*
*
Hilfsleitung 1
auto
*
*
*
*
*
Hilfsleitung 2
Mast
*
*
*
*
*
Trassenachse
Leitung
LeitungL2
*
*
*
*
*
*
*
*
*
*
*
*
*
Cu95
mm²
mm²
m/ Ωmm²
Ω/km
mm
*
*
*
*
*
*
*
*
-
Materialbezeichnung
Querschnitt 1
Querschnitt 2
spez. Leitfähigkeit
Widerstandsbelag
äquiv. Durchmesser
0*
0*
*
*
*
*
*
*
-
Profiltyp:
X/m
standard1
Y/m
Trak tionsstrom It/A
U/V *
150
U/° *
0 deltaU/V *
Nennspannung
deltaU/° *
15000
I/A *
0
I/° *
Horizontalwinkel
0°
Hilfsleitung 1
GR1
-
auto
Trassenachse
Leitung
LeitungL1
16,67 Hz
2
-
2
Gleise / Leitungen
Frequenz
100 Ohm m
-180 A/°
-
20.01.2005
*
*
*
*
*
Abbildung 4.6 : Auszug aus dem Reportblatt (MF-Calc-railway)
Peter Unterwieser
Seite 40
Rechenbeispiel zu MF-Calc-railway
Die Modellierung im Programm MF-Calc-railway erfolgte folgendermaßen:
Jeder einzelne Leiter wird als Leitung eingegeben. Daraus folgt, dass es 2 Objekte gibt, bei
denen der Strom vorgegeben werden kann.
Der Widerstandsbelag und der Durchmesser der Leiter haben für diese Anordnung keine
Auswirkung auf das Berechnungsergebnis. Die Ströme der Leiter sind hier eingeprägt. Die
Erde ist der einzige Rückleiter d. h. es muss keine Aufteilung der Rückleiterströme berechnet
werden. Deshalb können beliebige Werte angenommen werden.
10,0
9,0
8,0
7,0
6,0
5,0
4,0
Y
3,0
2,0
Leitung0
Leitung1
250A 0°
150A
GR2
GR1
1,0
0,0
-1,0
-2,0
-3,0
-4,0
9,0
10,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-5,0
TU-Graz
A.Abart 2003
X
Abbildung 4.7 : Anordnung der Leiter
Peter Unterwieser
Seite 41
Rechenbeispiel zu MF-Calc-railway
10,0
9,0
8,0
10
40
100
10
5,0
20
4,0
10
Y
10
3,0
10
2,0
10
Leitung0
Leitung1
250A 0°
150A
GR2
GR1
1,0
0,0
-1,0
-2,0
10
-3,0
µT
20
6,0
30
20
> 500
< 500
< 400
< 300
< 200
< 100
< 50
< 40
< 30
< 20
< 10
< 5
< 4
< 3
< 2
< 1
< 0.5
< 0.4
< 0.3
< 0.2
< 0.1
< 0.05
< 0.04
< 0.03
< 0.02
< 0.01
< 0.005
< 0.004
< 0.003
< 0.002
< 0.001
7,0
10
-4,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-5,0
TU-Graz
A.Abart 2003
X
Abbildung 4.8 : Feldbild der Ersatzflußdichte
Um die Ersatzflussdichte im Aufpunkt besser ablesen zu können wurde ein Diagramm
gezeichnet. Das Diagramm der Ersatzflußdichte wurde für die in Abhängigkeit der X Achse
für die Position Y = 0 Meter gezeichnet. Das Diagramm geht genau durch unseren Aufpunkt,
der bei Y = 0 Meter liegt.
Querprofil magnetische Flussdichte mfcalc railway
Magnetische Ersatzflussdichte µT
1000
100
B- EFD
X-Komp.
10
Y-Komp.
1
TU Graz
A. Abart 2003
0,1
-10
-8
-6
-4
-2
0
2
4
6
8
10
Abstand vom Punkt X = 0, Y = 0 Meter
Abbildung 4.9 : Diagramm der mag. Ersatzflußdichte in der Aufpunktsebene
Peter Unterwieser
Seite 42
Rechenbeispiel zu MF-Calc-railway
Die magnetische Flussdichte ist im logarithmischen Maßstab dargestellt.
Im PROFILDAT Blatt von MF-Calc-railway sind die Daten für das gezeichnete Diagramm
hinterlegt. Die X Komponente, die Y Komponente und die EFD sind über die X Achse
aufgetragen. Für das Diagramm wurde im Berechnungsvorgang die X Achse ausgewählt. Aus
dem Tabellenblatt wurde ein Teil ausgeschnitten um die Übersichtlichkeit zu erhöhen. Das
Ergebnis der einzelnen Komponenten wurde rot markiert. Es stimmt mit der analytischen
Rechnung überein
X/m
-0,2
-2,0539E-15
0,2
B- EFD
X-Komp.
Y-Komp.
Z-Komp.
7,48204819 7,11912116 2,30199024
3,578E-15
7,8080224
7,4558677 2,31845865 3,6036E-15
8,12608549 7,77181434 2,37321876 3,6887E-15
Abbildung 4.10 : Auszug aus dem Profildatenblatt
Im RESULT Blatt von MF-Calc-railway sind die Daten für den gezeichneten Fieldplot
hinterlegt. Das heißt, die EFD aufgetragen über X-Position und Y-Position. Aus dem
Tabellenblatt wurde ein Teil ausgeschnitten um die Übersichtlichkeit zu erhöhen. Das
Ergebnis wurde rot markiert. Es stimmt mit der analytischen Rechnung überein.
X = -0,5
X=0
X = 0,5
Y = -0,5
7,48900605
8,01244606
8,53847741
Y=0
6,98529444
7,8080224
8,58261712
Y = 0,5
6,60725286
7,74168662
8,78035131
Abbildung 4.11 : Auszug aus dem Ergebnisblatt
Beim Vergleich sieht man, dass die Ergebnisse der analytischen Rechnung und die der
Simulation übereinstimmen. In der Abbildung 4.10 sieht man die EFD mit 7,8080 μT als
Ergebnis der Simulation. Die analytische Lösung ergab 7,8192 μT als Ergebnis. Die kleine
Abweichung im Bereich von 0,2% entsteht durch Rundungsfehler der Matrizenoperationen.
Peter Unterwieser
Seite 43
Magnetfeldmessung Grüntunnel
5 Magnetfeldmessung Grüntunnel
5.1 Allgemeines
Ein besonderer Dank geht an Herrn Dr. Gerold Punz von den Österreichischen
Bundesbahnen, und allen Mitarbeitern der Regionalstelle St. Pölten für die Organisation und
Mitarbeit an der Messung beim Grüntunnel nahe Loosdorf.
Aufgabe der Diplomarbeit ist es, den Einfluss von Kompensationsleitern auf die magnetische
Ersatzflussdichte bei elektrischen Bahnen zu bestimmen. Der beste Weg die Ergebnisse der
Simulation zu verifizieren ist, eine Messung durchzuführen.
Abbildung 5.1 : Bild vom Grüntunnel Blickrichtung Osten
Peter Unterwieser
Seite 44
Magnetfeldmessung Grüntunnel
5.2 Spezielle Anforderungen an den Messtunnel
Die Tunnelarmierung wird in der Simulation durch eine Anordnung von unendlich langen
Leitern modelliert. Diese Leiter sollen das Stahlgeflecht im Beton nachbilden, welches bei
Stahlbetonbauten verwendet wird. Daher wird für die Messung der Feldbeeinflussung eine
spezielle Tunnelbauweise benötigt. Es wird weiters ein Tunnel mit wenig Überdeckung
gesucht, um im Zuge einer Messung ein magnetisches Querprofil erstellen zu können. Das
magnetische Querprofil besteht aus einzelnen Messpunkten, die oberhalb des Tunnels entlang
einer Messtrasse aufgenommen werden. Mit Überdeckung ist das Erdreich über einem
Tunnelbauwerk gemeint.
Ein weiterer wichtiger Punkt ist, dass man bei der Messung möglichst nahe an diese
Armierungsleiter im Tunnel kommt, um brauchbare Messergebnisse zu erhalten.
Ein Tunnel, bei dem hohe Anforderungen an die Festigkeit gestellt werden, wird zumeist in
Stahlbetonbauweise errichtet. Jedoch weisen diese Stahlbetontunnel eine große Überdeckung
auf, und damit stehen diese beiden Forderungen meist im Widerspruch zueinander.
Mit Hilfe der Österreichischen Bundesbahnen wurde ein Tunnel gefunden, der den oben
genannten Anforderungen entspricht, nämlich der Grüntunnel bei Loosdorf cirka 20 km
westlich von St. Pölten. Er ist Teil der Westbahnstrecke die in diesem Abschnitt als
Hochgeschwindigkeitstrecke geführt wird.
Der Tunnel liegt unter der Autobahnabfahrt Loosdorf. Der in Stahlbetonbauweise
ausgeführte, 300 m lange Tunnel, mit einer maximalen Überdeckung von nur 1,5 Metern, ist
ein ideales Messobjekt. Die Gesamtlänge von 300 m reicht aus, um die auftretenden
Inhomogenitäten des Feldes am Tunnelanfang und - ende auszuschließen.
Peter Unterwieser
Seite 45
Magnetfeldmessung Grüntunnel
5.3 Die Ausführung der Messung
Um möglichst hohe Ströme und eine definierte Stromrichtung vorzugeben, wurde der
Leitungsabschnitt im Stich betrieben. Das bedeutet, dass der Tunnel nur von einer Seite mit
elektrischer Energie versorgt wurde. Im Umspannwerk Bergan wurden daher die
Leistungsschalter geöffnet und der Streckenabschnitt des Grüntunnels wurde nur vom
Umspannwerk Rohr betrieben. Zusätzlich wurde eine Strommessung im UW Rohr mittels
Datenlogger realisiert. Dieser Datenlogger speicherte alle 5 Sekunden einen Messwert für den
Strom. Dieser Messwert besteht aus einem Maximalen-, einem Minimalen- und einem
Durchschnittsstromwert.
Die Messung wurde am 4. Dezember 2003 durchgeführt.
Abbildung 5.2 : Skizze des Messvorganges
Dargestellt ist der genaue Verlauf der Messtrassen über dem Grüntunnel. Eingetragen ist die
Richtung der Achsen, die Reihenfolge und die Richtung der Messungen.
Peter Unterwieser
Seite 46
Magnetfeldmessung Grüntunnel
Die Eisenbahnstrecke macht in diesem Abschnitt eine leichte Biegung, deshalb wurde der
ungefähre Verlauf des Tunnels markiert. Dies geschah mit Stangen oberhalb des Tunnels.
Zuerst wurde ein Längsprofil erstellt, um charakteristische Werte zu finden und um
Verfälschungen
durch
Querbanderder
oder
ähnliches
auszuschließen.
Aus
diesen
Längsprofilen konnten unmittelbar bei der Messung keine Informationen entnommen werden,
da die zeitliche Änderung des Stromes zu groß war. Dies wurde erst bei der Auswertung der
Messwerte festgestellt.
Im UW Rohr wurden die Oberleitungsströme mittels Datenlogger der Österreichischen
Bundesbahnen gemessen und im folgenden Diagramm über die Zeit aufgetragen. Die Größe
der Ströme ist in Prozent, bezogen auf den Maximalwert, dargestellt.
100,0
90,0
80,0
70,0
60,0
50,0
40,0
30,0
20,0
10,0
0,0
0:00:00
0:00:05
0:00:10
0:00:15
0:00:20
0:00:25
0:00:30
0:00:35
0:00:40
0:00:45
0:00:50
0:00:55
0:01:00
0:01:05
0:01:10
0:01:15
0:01:20
0:01:25
0:01:30
0:01:35
0:01:40
0:01:45
0:01:50
0:01:55
0:02:00
0:02:05
0:02:10
0:02:15
0:02:20
0:02:25
0:02:30
0:02:35
Strom [%]
Variation des Stromes bei einer Längsmessung
Zeit [ h:min:sec ]
Abbildung 5.3 : Oberleitungsstrom in Abhängigkeit der Zeit
Peter Unterwieser
Seite 47
Magnetfeldmessung Grüntunnel
Zu erkennen ist die starke Änderung des Stromes. Um trotz der Änderung des Stromes richtig
zu messen wurde ein Messverfahren mit 2 Sonden gewählt. Eine detaillierte Beschreibung des
Verfahrens ist dem Abschnitt 2.5.3 zu entnehmen.
Danach wurden die gesuchten Querprofile gemessen. Dazu wurden Messpunkte von -20 m
bis +20 m bezüglich der Tunnellängsachse aufgenommen und in ein Diagramm eingetragen.
Es wurde versucht bei jedem Meter einen Messpunkt zu verwirklichen.
Peter Unterwieser
Seite 48
Magnetfeldmessung Grüntunnel
5.4 Simulation des magnetischen Feldes bei Bahnanlagen unter
Einfluss der Tunnelarmierung
Die Simulation wurde mit dem Programm MF-Calc-railway durchgeführt.
Abbildung 5.4 : Skizze des Grüntunnels mit allen Leitern
In der Skizze sind alle wichtigen Leiter eingezeichnet. Elektrische Traktionsleitungen sind das
Tragseil und der Fahrdraht. Als Rückleiter dienen Erdungsleitungen, Rückleiter, Handlauf,
Schiene und die Armierungsleiter im Tunnel. Alle Rückleiter sind miteinander galvanisch
verbunden. Der Rückstrom teilt sich entsprechend ihrer Impedanzen auf.
Peter Unterwieser
Seite 49
Magnetfeldmessung Grüntunnel
Abbildung 5.5 : Angenommene Position der Tunnelleiter
Abgebildet ist die genaue Position der Tunnelleiter des Grüntunnels. Die Koordinaten können
in die Tunneltabelle für die Simulation eingegeben werden.
Daten für die Simulation
Bezeichnung
A1
A2 Ohm/km Typ allg.
Armierungsleiter
100
0,195 Rückleiter
Erdungsleiter Kupfer
95
0,187 Rückleiter
Rückleiter Kupfer
150
0,119 Rückleiter
Handlauf
400
0,039 Rückleiter
5
5
5
5
Schätzung
Aus Erdungskonzept OEBB
Aus Erdungskonzept OEBB
Schätzung
( Normprofilrohr aus TB Metallechnik )
Abbildung 5.6 : Daten für die Simulation
Peter Unterwieser
Seite 50
Magnetfeldmessung Grüntunnel
Berechnung des Widerstandes pro Kilometer am Beispiel des Erdungsleiters aus Kupfer:
γKupfer=56 [ Sm/mm2 ]
R=
R=
10
l
[Ω]
γ ⋅A
GL. 5.1
1m
= 0,000187 [Ω]
Sm
2
56
⋅ 95mm
mm 2
R1000 m = R1m ⋅ 1000m = 0,187 [Ω] → R / km =
R
R
=
= 0,187 [Ω/km]
l 1km
Abschätzung des Widerstandes pro Kilometer der Armierungsleiter:
R=
l
[Ω]
γ ⋅A
γStahldraht= 5,88 [Sm/mm2]
11
Abschätzung des Minimalwiderstandes pro km:
In Stahlbeton werden ca. 26,8 cm2 Armierungsstahl pro m2 Beton verwendet. Diese Angabe
stammt von einem Fachmann der Bauindustrie. Für das Beispiel des Grüntunnels ergibt sich
bei einem Umfang von 37 Metern und einer Dicke vom durchschnittlich 0,7 Metern ein
Querschnitt von ca. 25,85 m2 Stahlbeton. Für die 32 Armierungsleiter in der Simulation ergibt
sich somit ein Wert von 0,807 Leitern pro Quadratmeter Tunnel.
Anzahl der Quadratmeter pro Ersatz Leiter:
Tunnelquerschnitt
25,85m 2
Anzahl =
=
= 0,807
Anzahl _ der _ Leiter
32
26,8 cm2/m2 ergibt 2680 mm2/m2 Armierungsstahl.
10
Friedrich, W.: Tabellenbuch Elektrotechnik Elektronik. ISBN 3-427-53024-8, Dümmlers Verlag, 1993
11
Weinmann, A .: ELIN Formeln und Fakten. ISBN 3-9500084-0-3, Firma ELIN, 1991
Peter Unterwieser
Seite 51
Magnetfeldmessung Grüntunnel
Gefragt ist nun der rechnerische Querschnitt eines Armierungsleiters in der Simulation. Bei
0,807 Leitern pro Quadratmeter und 2680 mm2/m2 Armierungsstahl ergibt sich:
Arechnerisch = 0,807
RMin =
Leiter
mm 2
⋅ 2680 2 = 2162,76 [mm2/m2]
m
m
1000m
= 0,0786 [Ω/km]
Sm
2
5,88
⋅
2162
,
76
mm
mm 2
Der Widerstand pro km liegt nun zwischen einem Maximalwert und dem Minimalwert von
0,0786 [Ω/km] pro Stab für unsere geometrische Anordnung in der Simulation. Weiters
besteht die Armierung nicht aus Stahlstäben sondern ist als Gitter mit mehreren
Querverbindungen ausgeführt. Über die Schweißverbindungen der Stahlstäbe entstehen so
mehrere Parallelschaltungen.
Der angenommene Widerstandswert pro km für einen Ersatzleiter mit 95 mm2 beträgt
0,195 [Ω/km]. Dieser Wert wurde von Experten bestätigt.
Das heißt, es ist daher für das Ergebnis der Simulation von großer Bedeutung, den Widerstand
der Armierungsleiter genau zu kennen. Am besten wäre eine Messung des genauen
Widerstandes. Das ist natürlich in der Planungsphase, in der die magnetischen Felder
abgeschätzt werden sollen, sehr schwierig. Wie groß der Einfluss des Widerstandes auf die
Simulation ist, kann man dem Diagramm in Abbildung 6.12 entnehmen.
Peter Unterwieser
Seite 52
Magnetfeldmessung Grüntunnel
1
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
> 500
< 500
< 400
< 300
< 200
< 100
< 50
< 40
< 30
< 20
< 10
< 5
< 4
< 3
< 2
< 1
< 0.5
< 0.4
< 0.3
< 0.2
< 0.1
< 0.05
< 0.04
< 0.03
< 0.02
< 0.01
< 0.005
< 0.004
< 0.003
< 0.002
< 0.001
2
2
12,0
3
11,0
10,0
10
10
3
9,0
8,0
Y
7,0
6,0
20
3,0
1
30
4,0
5
1
20
0.5
2
10
30
5,0
1,0
2
10
3
2,0
1
-1,0
5
0.4
0.5
5
0,0
X
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
TU-Graz
A.Abart 2003
Abbildung 5.7 : Magnetische Felder einer zweigleisigen Bahnanlage unter Einfluss eines
Tunnels
Dargestellt ist ein Querschnitt durch den Tunnel. Angenommen wurde der Traktionsstrom im
rechten Fahrdraht. Als Werte wurden 500 A als Traktionsstrom und 100 A als Hilfszuleitungsstrom (negativer Traktionsstrom) in der zweiten Oberleitung gewählt.
Peter Unterwieser
Seite 53
µT
13,0
Magnetfeldmessung Grüntunnel
Querprofil magnetische Flussdichte mfcalc railway
Magnetische Ersatzflussdichte µT
1000
100
B- EFD
X-Komp.
10
Y-Komp.
1
TU Graz
A. Abart 2003
0,1
-20
-15
-10
-5
0
5
10
15
20
Abstand vom Punkt X = 0, Y = 0 Meter
Abbildung 5.8 : Magnetische Ersatzflußdichte einer zweigleisigen Bahnanlage bei einem
Tunnel in der Höhe von ca. 10 m über der Sohlplatte des Tunnels
Peter Unterwieser
Seite 54
Magnetfeldmessung Grüntunnel
Messung des magnetischen Feldes bei Bahnanlagen mit einem Tunnel
Um die simulierten Werte mit den gemessenen vergleichen zu können, ist ein Diagramm mit
den Ersatzflussdichtewerten in der Höhe von ungefähr 10 m zu erstellen.
0,8
0,6
0,4
0,2
0,0
1,1
2,2
3,3
4,4
5,6
6,7
7,8
8,9
10,0
11,1
12,2
13,3
14,4
15,6
16,7
17,8
18,9
20,0
21,3
22,5
23,8
25,0
26,3
27,5
28,8
30,0
31,3
32,5
33,8
35,0
36,3
37,5
38,8
40,0
41,3
42,5
43,8
45,0
46,3
47,5
48,8
50,0
51,3
52,5
53,8
55,0
Bez. mag. Flußdichte
[1]
1,0
Bezogene mag. Ersatzflußdichte
Tunnelachse
Abstand [ m ]
Abbildung 5.9 : Bezogene magnetische Ersatzflußdichte einer zweigleisigen Bahnanlage in
einem Tunnel in der Höhe von ca. 10 m über der Gleisebene des Tunnels (Messung M1 quer)
Die Werte des in Abbildung 5.9 dargestellten Diagrammverlaufs sind mit Hilfe eines 2Sonden-Messverfahrens ermittelt worden. Die Symmetrieachse des Tunnels hat einen
Abstand von 19 m im Diagramm. Die Messwerte der mobilen Sonde werden immer bezogen
auf die Messwerte der festen Sonde zum gleichen Zeitpunkt. Sie sind im Diagramm als
bezogene magnetische Flussdichte aufgetragen. Ein Zahlenwert von 1 würde in dieser
Darstellung nur bedeuten, dass der Wert der mobilen und der Wert der festen Sonde für den
betrachteten Zeitpunkt gleich groß sind.
Peter Unterwieser
Seite 55
Magnetfeldmessung Grüntunnel
5.5 Vergleich der Messung mit der Simulation
Es werden die einzelnen Komponenten des magnetischen Feldes und die EFD der Messung
und der Simulation miteinander verglichen. Dazu wurden berechnete und simulierte Werte
gemeinsam in ein Diagramm eingetragen.
Zur leichteren Orientierung ist die Tunnelachse (Symmetrieachse des Tunnels) in die
Darstellungen eingezeichnet. Bei der Simulation wurde ein Traktionsstrom mit 500 A
angenommen, da dies besser zur realen Situation passt. Im Unterschied zu den Abbildungen
in Abschnitt 5.4, dort wurden ein Traktionsstrom von 500 A und ein Hilfszuleitungsstrom von
-100 A in der Oberleitung verwendet.
5.5.1 Messung 1 in Querrichtung zur Tunnelachse
Bezogene mag. Ersatzflußdichte und Komponenten
Tunnelachse
0,8
EFD
0,6
0,4
BY
BX
0,2
0,0
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
11,0
12,0
13,0
14,0
15,0
16,0
17,0
18,0
19,0
20,0
21,0
22,0
23,0
24,0
25,0
26,0
27,0
28,0
29,0
30,0
31,0
32,0
33,0
34,0
35,0
36,0
37,0
38,0
39,0
Bez. mag. Flußdichte
[1]
1,0
Abstand [ m ]
Abbildung 5.10: Magnetische Ersatzflußdichte einer zweigleisigen Bahnanlage bei einem
Tunnel in der Höhe von ca. 10 m über der Sohlplatte des Tunnels.
Aus der Abbildung 5.10 ist der Verlauf der EFD (blau) und der Komponenten in X- (grün)
und Y-Richtung (schwarz) zu erkennen. Dieser Verlauf ist mit MF-Calc-railway simuliert.
Peter Unterwieser
Seite 56
Magnetfeldmessung Grüntunnel
Bezogene mag. Flußdichte in X-Richtung
Tunnelachse
0,8
BX_Simuliert
0,6
0,4
BX_Gemessen
0,2
0,0
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
11,0
12,0
13,0
14,0
15,0
16,0
17,0
18,0
19,0
20,0
21,0
22,0
23,0
24,0
25,0
26,0
27,0
28,0
29,0
30,0
31,0
32,0
33,0
34,0
35,0
36,0
37,0
38,0
39,0
Bez. mag. Flußdichte
[1]
1,0
Abstand [ m ]
Abbildung 5.11 : Vergleich der Rechnung und der Messung der bezogenen mag. Flussdichte
in X Richtung einer zweigleisigen Bahnanlage in einem Tunnel in der Höhe von ca. 10 m
über der Sohlplatte des Tunnels (Messung M1 quer)
In der Abbildung 5.11 ist in Rot der gemessene Verlauf der mag. Flussdichte in X-Richtung
aufgetragen. Im Vergleich dazu in Grün der simulierte Verlauf der mag. Flussdichte in XRichtung. Zu erkennen ist ein ähnlicher Verlauf.
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0,0
Tunnelachse
BY_Simuliert
BY_Gemessen
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
11,0
12,0
13,0
14,0
15,0
16,0
17,0
18,0
19,0
20,0
21,0
22,0
23,0
24,0
25,0
26,0
27,0
28,0
29,0
30,0
31,0
32,0
33,0
34,0
35,0
36,0
37,0
38,0
39,0
Bez. mag. Flußdichte
[1]
Bezogene mag. Flußdichte in Y-Richtung
Abstand [ m ]
Abbildung 5.12. : Vergleich der Rechnung und der Messung der bezogenen mag. Flussdichte
in Y Richtung einer zweigleisigen Bahnanlage in einem Tunnel in der Höhe von ca. 10 m
über der Sohlplatte des Tunnels (Messung M1 quer)
Peter Unterwieser
Seite 57
Magnetfeldmessung Grüntunnel
In der Abbildung 5.12 ist in Rot der gemessene Verlauf der mag. Flussdichte in Y-Richtung
aufgetragen. Im Vergleich dazu in Schwarz der simulierte Verlauf der mag. Flussdichte in YRichtung. Man erkennt das der Verlauf der Komponenten der magnetischen Flussdichte der
Rechnung und der Messung ähnlich sind. Ähnliche Maxima und Minima sind ersichtlich.
Bezogene mag. Ersatzflußdichte
Tunnelachse
0,8
0,6
EFD_Gemessen
EFD_Simuliert
0,4
0,2
0,0
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
11,0
12,0
13,0
14,0
15,0
16,0
17,0
18,0
19,0
20,0
21,0
22,0
23,0
24,0
25,0
26,0
27,0
28,0
29,0
30,0
31,0
32,0
33,0
34,0
35,0
36,0
37,0
38,0
39,0
Bez. mag. EFD [ 1 ]
1,0
Abstand [ m ]
Abbildung 5.13 : Vergleich der Rechnung und der Messung der bezogenen mag.
Ersatzflußdichte einer zweigleisigen Bahnanlage in einem Tunnel in der Höhe von ca. 10 m
über der Sohlplatte des Tunnels (Messung M1 quer)
In der Abbildung 5.13 ist in Rot der gemessene Verlauf der EFD aufgetragen. Im Vergleich
dazu in Violett der simulierte Verlauf der EFD. Man erkennt das der Verlauf der EFD der
Rechnung und der Messung vergleichbare Gestalt haben.
Auch der gemessene Maximalwert der EFD von 8,2 μT passt zur Rechnung.
Je weiter die Messorte von der Tunnelachse entfernt sind desto größer wird für sie der Fehler.
Dieser Fehler entsteht da ihre absolute Größe nur ein Buchteil vom Maximum ist.
Peter Unterwieser
Seite 58
Magnetfeldmessung Grüntunnel
Mag. Ersatzflußdichte der festen Sonde
entspricht dem Strom
8,0
feste Sonde
6,0
f (x0,t)
4,0
mobile Sonde
2,0
0,0
f (x,t)
00:00
00:02
00:06
00:10
00:13
00:17
00:19
00:23
00:28
00:33
00:37
00:41
00:46
00:50
00:56
00:59
01:04
01:08
01:12
01:17
01:20
01:24
01:29
01:33
01:37
01:40
01:44
01:48
01:50
01:54
01:57
02:01
02:05
02:11
02:16
02:23
02:28
02:33
02:38
02:42
02:47
02:51
02:56
02:59
03:03
03:08
Magnetische EFD
[μ T ]
10,0
Zeit [sec]
Abbildung 5.14 : Ergebnisse der Messung der bezogenen mag. Ersatzflußdichte der festen
und der mobilen Sonde einer zweigleisigen Bahnanlage in einem Tunnel in der Höhe von ca.
10 m über der Sohlplatte des Tunnels (Messung M1 quer)
Die Abbildung 5.14 zeigt die Abhängigkeit der EFD der Sonden von der Zeit für die Dauer
der Messung. Die mag. Ersatzflußdichte der festen Sonde ist proportional dem Strom in der
Oberleitung.
Zu erkennen ist die starke Änderung des Stromes im Messzeitraum. Die schnelle Änderung
wirkt sich auf die Messfehler aus. Mit Hilfe besserer Synchronisation der mobilen und der
festen Sonde könnte die Messfehler des Messverfahrens entscheidend verbessert werden. Die
beiden Messgeräte könnten über den Datenübertragungsdienst eines Mobilfunkanbieters
verbunden werden und Messwerte austauschen. Damit könnte eine Echtzeitkorrelation
durchgeführt werden und so die Messpunkte während der Messung nach ihrer Aussagekraft
beurteilt werden. Das beschriebene Messverfahren heißt Flying Carpet und ist in der
Diplomarbeit von Andreas Fürst entwickelt worden.
Weiters wirkt sich der Fahrzustand des Zuges auf den Strom aus. Der oben dargestellte
Verlauf könnte beispielsweise einen Beschleunigungsvorgang darstellen.
Peter Unterwieser
Seite 59
Reduktionsfaktorenrechnung mit MF-Calc-railway
6 Reduktionsfaktorenrechnung mit MF-Calc-railway
6.1 Allgemeines
Mit der Hilfe von MF-Calc-railway kann der Verlauf der magnetischen Felder dargestellt
werden. Zur besseren Übersichtlichkeit wurde eine Differenzdarstellung erarbeitet. Sie stellt
die Differenz der örtlich veränderlichen Feldverhältnisse mit und ohne Einfuß der
Tunnelarmierung dar.
Zur Berechnung wurde die geometrische Kompensationsleiter ohne Vergleichsleiter mit Hilfe
von MF-Calc-railway nachgebildet und die EFD berechnet. Die Ersatzflussdichte des
magnetischen Feldes kann aus dem Ergebnisblatt entnommen werden. In diesem Blatt wird
die Ersatzflussdichte des magnetischen Feldes in Abhängigkeit der X und Y Position
dargestellt. Danach wird die gleiche geometrische Anordnung unter Einfluss der
Kompensationsleiter berechnet. Es kann nun die Differenz der beiden Rechnungen gebildet
werden. Die Differenz wird bezogen auf die Ersatzflussdichte des magnetischen Feldes ohne
Tunnelarmierung und in Prozent dargestellt. Mit der Feldänderung in Prozent kann nun ein
eigenes Bild erstellt werden, genannt die relative Änderung. Diese stellt die Änderung zweier
zu vergleichender Zustände der Ersatzflussdichte des magnetischen Feldes in Falschfarbendarstellung dar.
Aufgrund der Diskretisierung in MF-Calc-railway können zufällig hohe EFD berechnet
werden, die sich in der Nähe der Leiter ergeben. Dies ist dann der Fall wenn die
Leiterposition und die Position des Rechenwertes genau zusammenfallen. Diese
Übereinstimmung entspricht einer Division durch null deren Ergebnis unendlich groß wäre.
Diese Werte der EFD wurden in der Berechnung der Änderungen und Reduktionsfaktoren
aussortiert.
Peter Unterwieser
Seite 60
Reduktionsfaktorenrechnung mit MF-Calc-railway
Relative Änderung
ΔEFDRe lativ =
EFDmitTunnel
⋅ 100
EFDohneTunnel
ΔEFDRelativ
…relative Änderung der Ersatzflussdichte des magnetischen Feldes in %
[%]
GL. 6.1
EFDohneTunnel …Ersatzflussdichte des magnetischen Feldes ohne den Einfluss der
Tunnelarmierung in μT
EFDmitTunnel
…Ersatzflussdichte des magnetischen Feldes mit Einfluss der
Tunnelarmierung in μT
Als Beispiel 25 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 0,25 μT
verringert hat.
Bei einer Skalierung mit einem Maximum von 150 % können Verkleinerungen der EFD als
Differenzen unter 100 % abgelesen werden. Vergrößerungen sind als Differenzen größer als
100 % abgebildet. Wenn sich die EFD von dem Wert 1,0 μT ohne Tunnelleiter auf den Wert
1,5 μT mit Tunnelleiter ändert, so bedeutet dies eine relative Abweichung von 150 %. Diese
Verschlechterung der Reduktionswirkung könnte im Bereich der Oberleitungen auftreten
(siehe Abbildung 6.6).
Alle relativen Feldverläufe werden nachfolgend mit dem gleichen Skalenmaximalwert von
150 % gezeichnet, um sie untereinander vergleichen zu können.
Peter Unterwieser
Seite 61
Reduktionsfaktorenrechnung mit MF-Calc-railway
Flächenbezogene Ersatzflussdichtereduktionsfaktor
Die relativen Änderungen sind über die Abbildung sehr ungleichmäßig verteilt. Um die
nachfolgenden Differenzdarstellungen besser miteinander vergleichen zu können, wurde ein
flächenbezogener Ersatzflussdichtereduktionsfaktor für das gesamte Feldbild errechnet.
Dieser ergibt sich aus der Summe aller im Bild dargestellten Änderungen der
Ersatzflussdichten, dividiert durch die Anzahl der Änderungen der Ersatzflussdichten. Der
Reduktionsfaktor stellt somit den arithmetischen Mittelwert der Änderungen der EFD im
betrachteten Ausschnitt dar.
Für die 30 x 17 Meter Bilder mit einer Unterteilung von 0,5 Meter ergeben sich so 2165
errechnete Punkte (35 x 61). Der flächenbezogene Ersatzflussdichtereduktionsfaktor ist also
der Mittelwert aus 2165 Einzelwerten der Änderung der EFD.
Für die 160 x 82 Meter Bilder mit einer Unterteilung von 2 Meter ergeben sich so 3402
errechnete Punkte (81 x 42). Der flächenbezogene Ersatzflussdichtereduktionsfaktor ist also
der Mittelwert aus 3402 Einzelwerten der Änderung der EFD.
Berechnung des Reduktionsfaktors:
Reduktionsfaktor =
ΔEFD
1 x=n y =m
∑ ∑ ΔEFDn,m
n ⋅ m x=1 y =1
[%]
GL. 6.2
…Änderung der Ersatzflussdichte des magnetischen Feldes in %, siehe
GL. 6.1
x, y
…Raumkoordinaten in x und y Richtung
n
…Anzahl der gerechneten Punkte in x Richtung
m
…Anzahl der gerechneten Punkte in y Richtung
Peter Unterwieser
Seite 62
Reduktionsfaktorenrechnung mit MF-Calc-railway
6.2 Reduktionswirkung an Hand eines Beispiels
Die im Folgenden gewählte Anordnung entspricht dem Grüntunnel. Die Felder ohne den
Einfluss der Tunnelarmierung sollen mit den Feldern mit Einfluss der Armierung des
Grüntunnels verglichen werden. Als erstes wird die geometrische Anordnung der Leiter
dargestellt und anschließend der Feldverlauf der EFD errechnet.
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
13,0
12,0
11,0
10,0
9,0
8,0
Y
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
X
TU-Graz
A.Abart 2003
Abbildung 6.1 : Leiteranordnung ohne Armierungsleiter in MF-Calc-railway
Peter Unterwieser
Seite 63
Reduktionsfaktorenrechnung mit MF-Calc-railway
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
3
12,0
10,0
9,0
20
4
5
5
4
11,0
10
8,0
Y
7,0
20
5
40
6,0
5,0
30
4,0
3,0
5
30
20
10
0,0
4
2
1,0
3
4
3
2,0
> 500
< 500
< 400
< 300
< 200
< 100
< 50
< 40
< 30
< 20
< 10
< 5
< 4
< 3
< 2
< 1
< 0.5
< 0.4
< 0.3
< 0.2
< 0.1
< 0.05
< 0.04
< 0.03
< 0.02
< 0.01
< 0.005
< 0.004
< 0.003
< 0.002
< 0.001
-1,0
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
TU-Graz
A.Abart 2003
X
Abbildung 6.2 : EFD der Anordnung ohne Armierungsleiter
Der Grüntunnel soll mit der Hilfe von 32 Armierungsleitern in der Simulation nachgebildet
werden. Im rechten Schienensystem wird ein Traktionsstrom von 500 A angenommen. Die
Annahmen und die Bezeichnung der Leiter sind im Abschnitt 5.4 genauer beschrieben.
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
13,0
12,0
11,0
10,0
9,0
8,0
Y
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
X
TU-Graz
A.Abart 2003
Abbildung 6.3 : Leiteranordnung mit Tunnelleitern in MF-Calc-railway
Peter Unterwieser
Seite 64
µT
3
13,0
Reduktionsfaktorenrechnung mit MF-Calc-railway
1
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
13,0
3
11,0
10,0
10
10
3
9,0
8,0
Y
7,0
6,0
20
3,0
1
30
4,0
5
1
20
0.5
2
10
30
5,0
1,0
2
10
3
2,0
1
-1,0
5
0.4
0.5
5
0,0
> 500
< 500
< 400
< 300
< 200
< 100
< 50
< 40
< 30
< 20
< 10
< 5
< 4
< 3
< 2
< 1
< 0.5
< 0.4
< 0.3
< 0.2
< 0.1
< 0.05
< 0.04
< 0.03
< 0.02
< 0.01
< 0.005
< 0.004
< 0.003
< 0.002
< 0.001
µT
2
2
12,0
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
TU-Graz
A.Abart 2003
X
Abbildung 6.4 : EFD der Anordnung mit Tunnelleiter
Nun wird die relative Differenz der EFD in Abbildung 6.2 und in Abbildung 6.4 gebildet und
in Abbildung 6.5 in Prozent des unbeeinflussten Wertes dargestellt.
15,0
Gleis1
500A 0°
GR2
14,0
50
13,0
12,0
50
45
11,0
55
10,0
9,0
50
60
40
50
8,0
Y
45
65
7,0
6,0
45
40
75
40
4,0
3,0
40
2,0
55
35
1,0
0,0
30
25
55
40
X
15,0
14,0
13,0
12,0
-2,0
11,0
9,0
10,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
50
35
-1,0
TU-Graz
A.Abart 2003
Abbildung 6.5 : Relative Änderung der EFD in %12
12
125 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,25 μT ändert
Peter Unterwieser
Seite 65
%
5,0
35
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
µT
45
45
MFCALC Railway Version Sbb.1.0
Gleis0
0A 0°
GR1
Reduktionsfaktorenrechnung mit MF-Calc-railway
Aus der relativen Änderung kann nun genau ermittelt werden ob sich die EFD erhöht oder
verringert. Eine Erhöhung der EFD ergibt Werte über 100 % und Farben im grünen Bereich.
Eine Verringerung der EFD ergibt Werte unter 100 % und Farben im gelben und im blauen
Bereich. Man erkennt die größte „Verschlechterung“ im Bereich der Tunnelleiter oberhalb
des traktionsstromführenden Fahrdrahtes.
Außerdem ist die Reduktionswirkung in der linken Hälfte des Bildes größer als in der rechten
Hälfte. Dies ist bedingt durch die Wahl des Stromes im rechten Schienensystem.
Die Reduktionswirkung ist nicht gleichmäßig verteilt. Es bestehen Unterschiede von bis zu
70 %. Aus der Änderung der EFD des Bildes kann man den flächenbezogenen
Ersatzflussdichtereduktionsfaktor ausrechnen. Der genaue Berechnungsvorgang ist Gl. 6.2 zu
entnehmen. Aufgetragen über den ganzen Querschnitt stellt er die Reduktionswirkung der
Tunnelarmierung dar. Diese errechnet sich aus der Summe der Differenzen der
Ersatzflussdichten aller Punkte in X- und Y-Richtung gebrochen durch die Anzahl der
Punkte. Für die Abbildung 6.5 beträgt die Schrittweite 0,5 Meter. Die flächenbezogene
Ersatzflussdichtereduktion der Abbildung 6.5 beträgt 46,63 %. Das bedeutet, dass sich für
einen Querschnitt von 30 x 17 Meter die EFD unter Einfuß der Tunnelarmierung im
Durchschnitt um 46,63 % reduziert.
Peter Unterwieser
Seite 66
Reduktionsfaktorenrechnung mit MF-Calc-railway
Um den weiteren Verlauf der Feldreduktion im Fernbereich des Tunnels zu untersuchen
wurde ein größerer Ausschnitt gewählt. Die Größe des gewählten Ausschnittes beträgt 160 x
78,0
74,0
70,0
66,0
62,0
58,0
54,0
50,0
46,0
42,0
38,0
34,0
30,0
26,0
22,0
18,0
14,0
10,0
6,0
2,0
-2,0
0.2
0.3
1
0.5
0.2
0.4
0.4
0.3
76,0
70,0
64,0
58,0
52,0
46,0
40,0
34,0
28,0
22,0
16,0
4,0
10,0
-2,0
-8,0
-14,0
-20,0
0.5
1
20
0.4
-26,0
-32,0
0.2
-38,0
-44,0
-50,0
-56,0
-62,0
-68,0
-74,0
-80,0
> 500
< 500
< 400
< 300
< 200
< 100
< 50
< 40
< 30
< 20
< 10
< 5
< 4
< 3
< 2
< 1
< 0.5
< 0.4
< 0.3
< 0.2
< 0.1
< 0.05
< 0.04
< 0.03
< 0.02
< 0.01
< 0.005
< 0.004
< 0.003
< 0.002
< 0.001
µT
Gleis1
500A 0°
GR2
0.2
Gleis0
0A 0°
GR1
Y
82 Meter.
X
TU-Graz
A.Abart 2003
0.0
0.1
0.2
0.2
> 500
< 500
< 400
< 300
< 200
< 100
< 50
< 40
< 30
< 20
< 10
< 5
< 4
< 3
< 2
< 1
< 0.5
< 0.4
< 0.3
< 0.2
< 0.1
< 0.05
< 0.04
< 0.03
< 0.02
< 0.01
< 0.005
< 0.004
< 0.003
< 0.002
< 0.001
76,0
70,0
64,0
58,0
52,0
46,0
40,0
34,0
28,0
22,0
16,0
4,0
10,0
-2,0
-8,0
-14,0
-20,0
-26,0
0.1
-32,0
0.0
-38,0
-44,0
-50,0
0.0
-56,0
-62,0
3
10
1
0.3
0.3
0.0
0.03
-68,0
-74,0
-80,0
78,0
74,0
70,0
66,0
62,0
58,0
54,0
50,0
46,0
42,0
38,0
34,0
30,0
26,0
22,0
18,0
14,0
10,0
6,0
2,0
-2,0
X
TU-Graz
A.Abart 2003
Abbildung 6.7 : EFD der Anordnung mit Armierungsleiter als großer Ausschnitt
Peter Unterwieser
Seite 67
µT
Gleis1
500A 0°
GR2
0.0
Gleis0
0A 0°
GR1
Y
Abbildung 6.6 : EFD der Anordnung ohne Armierungsleiter als großer Ausschnitt
Reduktionsfaktorenrechnung mit MF-Calc-railway
Es kann nun wieder die relative Differenz gebildet und in einem Differenzfeldbild dargestellt
35
30
35
40
25
76,0
70,0
64,0
58,0
52,0
46,0
40,0
34,0
28,0
22,0
16,0
10,0
4,0
-2,0
-8,0
-14,0
-20,0
-26,0
-32,0
-38,0
-44,0
-50,0
-56,0
-62,0
-68,0
-74,0
-80,0
35
25
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
X
TU-Graz
A.Abart 2003
Abbildung 6.8 : Relative Änderung der EFD in %13 als großer Ausschnitt
Das Bild zeigt die Reduktionswirkung im Fernbereich des Tunnels als relative Änderung. Die
Reduktionswirkung im Nahbereich ist in der kleineren Abbildung 6.5 besser zu sehen. Die
Reduktionswirkung ist nicht gleichmäßig verteilt. Es bestehen Unterschiede von bis zu 70 %.
Weiters ist die Reduktionswirkung bedingt durch die Wahl des Stromes im rechten
Schienensystem in der linken Hälfte des Bildes größer als in der rechten.
Der flächenbezogene Ersatzflussdichtereduktionsfaktor der Abbildung 6.8 beträgt 31,73 %.
Im Vergleich dazu betrug der flächenbezogene Ersatzflussdichtereduktionsfaktor im
Nahbereich, dargestellt in Abbildung 6.5 nur 46,63 %. In den größeren Abbildungen erhält
man für die gleiche Leiteranordnung eine bessere Reduktionswirkung. Da der
flächenbezogene Ersatzflussdichtereduktionsfaktor ein Mittelwert ist, kommt hier die bessere
Reduktionswirkung im Außenbereich des Tunnels stärker zu tragen.
Hierbei ist zu beachten, dass im Fall der relativen Änderung kleinere Zahlenwerte eine
größere Reduktionswirkung bedeuten.
13
125 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,25 μT ändert
Peter Unterwieser
Seite 68
%
78,0
74,0
70,0
66,0
62,0
58,0
54,0
50,0
46,0
42,0
38,0
34,0
30,0
26,0
22,0
18,0
14,0
10,0
6,0
2,0
-2,0
µT
Gleis1
500A 0°
GR2
MFCALC Railway Version Sbb.1.0
Gleis0
0A 0°
GR1
Y
werden.
Reduktionsfaktorenrechnung mit MF-Calc-railway
6.3 Allgemeine Einflüsse auf die Reduktionswirkung
Die folgenden Reduktionsdiagramme wurden mit der Hilfe von MF-Calc-railway erarbeitet,
die Reduktionswirkung mit Hilfe vom Excel berechnet. In den Diagrammen ist die relative
Änderung aufgetragen. Die unterschiedlichen Fälle wurden dann in Diagrammen verglichen.
Grundlage für die Simulation ist eine zweigleisige Strecke wie sie schon in den Abschnitten
davor verwendet wurde. Als Ströme wurden 1000 A im rechten und 1000 A im linken
Gleissystem angenommen. Jedes Gleissystem hat einen Fahrdraht, ein Tragseil, eine
Verstärkungsleitung und eine Rückleitung in Standardanordnung. Die Tunnel haben einen
rechteckigen Querschnitt. Die Werte der EFD wurden einen Meter über der Gleisoberkante
gerechnet.
Als Erstes wurde die relative Änderung der EFD in Abhängigkeit von der Anzahl der
Armierungsleiter untersucht.
Ersatzflußdichtereduktion - Armierungszunahme
Relative Differenz [EFD/EFDo]
2,5
Abstand in[m]
80m
70m
60m
50m
40m
30m
20m
10m
9m
8m
7,6m
2
1,5
1
0,5
0
0
10
20
30
40
50
Anzahl Armierungen
Abbildung 6.9 : Abhängigkeit der relativen Änderung der EFD von der Anzahl der
Armierungsleiter
Peter Unterwieser
Seite 69
Reduktionsfaktorenrechnung mit MF-Calc-railway
Aufgetragen ist die relative Änderung in Bezug auf die Anzahl der Armierungsleiter. Diese
sind symmetrisch angeordnet und ihre Anzahl wird fortlaufend von der Symmetrieachse aus
erhöht. Als weitere Einflussgröße ist der Abstand vom Tunnel dargestellt. Der Abstand ist
gekennzeichnet durch die Linien unterschiedlicher Farbe.
Ab einem Abstand von ca. 9 Metern nimmt die Abschwächung ab, bei kleinerem Abstand
kann sie, wie schon vorher im Abschnitt 6.2 zu sehen ist, sogar zunehmen.
In der folgenden Abbildung wurde der Widerstand der Armierungsleiter verringert und die
Auswirkung auf die relative Änderung aufgetragen. Die Farben der Kurven geben die
Abhängigkeit vom Abstand wieder. Als Ausgangswert ist hier 0,195 Ω/km angenommen.
Dieser Wert entspricht dem angenommenen Widerstandsbelag der Kompensationsleiter aus
dem Grüntunnel. Deshalb hat die relative Änderung in der Abbildung 6.10 den Wert 1 für
0,195 Ω/km.
Ersatzflussdichtenreduktion - Widerstandsänderung
Relative Differenz [EFD/EFDo]
1,5
Abstand in[m]
80m
70m
60m
50m
40m
30m
20m
10m
9m
8m
7,6m
1
0,5
0
0
0,05
0,1
0,15
0,2
0,25
0,3
Widerstandsbelag [Ohm/km]
Abbildung 6.10 : Abhängigkeit der relativen Änderung der EFD vom Widerstandsbelag der
Armierungsleiter
Peter Unterwieser
Seite 70
Reduktionsfaktorenrechnung mit MF-Calc-railway
Man erkennt, dass eine Reduktion des Widerstandes zu einer sehr guten EFD Reduktion führt.
Durch den geringeren Widerstand fließen in den Armierungsleitern höhere Rückströme. Die
Ströme in der Armierung fließen gegen die Richtung der feldverursachenden Ströme und
erzeugen so Felder, die gegen die verursachenden Felder wirken. Diese höheren Ströme
reduzieren das Feld stärker als zuvor. Bei Tunnelbauwerken ist das jedoch sehr schwierig, da
eine Widerstandsreduktion einen anderen Werkstoff oder einen größeren Leiterdurchmesser
bedeuten würde. Stahlbeton ist aber nur mit Stahlarmierungsleitern technisch ausführbar. Auf
einer freien Strecke könnte eine Widerstandsreduzierung zur Feldreduktion eingesetzt
werden. Diese Idee wird im Abschnitt 0 genauer untersucht.
Wie aus der Abbildung 6.10 zu entnehmen ist, ist der Einfluss des Widerstandes sehr
bedeutend, daher ist eine Abschätzung des Widerstandes der Stahlarmierung im Beton von
größter Bedeutung für das Ergebnis der Simulation.
Als praktisches Beispiel dient die in den Boden gehende Unterflurtrasse, als eine schräge
Ebene nach unten. Die Schienen gehen vom Niveau des Erdbodens auf einer gewissen Länge
auf das Niveau des Tunnels nach unten.
Ersatzfussdichtenreduktion - Unterflurtrasseneinfahrt
Relative Differenz [EFD/EFDo]
2
Abstand in[m]
80m
70m
60m
50m
40m
30m
20m
10m
9m
8m
7,6m
1,5
1
0,5
0
0
4
8
12
16
Anzahl Tunnelleiter vertikal
Abbildung 6.11 : Einfluss der Zahl der Tunnelleiter auf die relative Änderung
Man sieht, je weiter man mit der Schnittebene in den Tunnel geht, desto größer die
Reduktionswirkung im Außenbereich.
Peter Unterwieser
Seite 71
Reduktionsfaktorenrechnung mit MF-Calc-railway
6.4 Reduktionswirkung auf der freien Stecke
Es stellt sich nun die Frage, welchen Einfluss hat der Rückleiter auf der freien Strecke auf die
magnetische EFD?
Um dieser Frage nachzugehen, wurde wieder eine Differenzdarstellung gebildet. Sie ist
bezogen auf die freie Strecke ohne Rückleiter.
Gewählt wurde ein 2 Schienensystem in Standardanordnung mit je 1000 A Traktionsstrom.
Gleis0
1000A 0°
GR1
15,0
Gleis1
1000A 0°
GR2
14,0
13,0
12,0
11,0
10,0
9,0
8,0
Y
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
X
TU-Graz
A.Abart 2003
Abbildung 6.12 : Standardanordnung der freien Strecke ohne Rückleiter
Zu sehen sind 2 Gleissysteme in Standardanordnung mit je 1000 A Traktionsstrom. Das Bild
enthält Fahrdraht, Tragseil, Verstärkungsleitung aber keine Rückleiter. Die Abbildung 6.12
stellt jene Anordnung dar, mit der die nachfolgende Anordnung mit dem Rückleiter
verglichen wird.
Peter Unterwieser
Seite 72
Reduktionsfaktorenrechnung mit MF-Calc-railway
Gleis0
1000A 0°
GR1
15,0
Gleis1
1000A 0°
GR2
14,0
13,0
12,0
11,0
10,0
9,0
8,0
Y
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
X
TU-Graz
A.Abart 2003
Abbildung 6.13 : Standardanordnung der freien Strecke mit Rückleiter
Zu sehen ist die gleiche Leiteranordnung wie in Abbildung 6.12, nur mit zusätzlich einem
Rückleiter je Gleissystem.
Das nachfolgende Bild ist auf ein Maximum von 150 % normiert. Das garantiert eine
optimale Vergleichbarkeit der Darstellungen. Für die Skalierung und die Darstellung gelten
wieder gleiche Voraussetzungen wie in Abschnitt 6.2 beschrieben.
Peter Unterwieser
Seite 73
Reduktionsfaktorenrechnung mit MF-Calc-railway
Gleis0
1000A 0°
GR1
15,0
Gleis1
1000A 0°
GR2
14,0
9,0
8,0
75
75
70
Y
7,0
80
6,0
5,0
65
90
70
85
65
85
4,0
3,0
70
80
2,0
80
1,0
0,0
80
-1,0
15,0
14,0
13,0
12,0
11,0
9,0
10,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
X
TU-Graz
A.Abart 2003
Abbildung 6.14 : Relative Änderung der EFD in %14 mit und ohne RL
Der flächenbezogene Ersatzflussdichtereduktionsfaktor der Abbildung 6.14 beträgt 82,47 %.
Für das Differenzbild im Fernbereich ergibt sich eine noch größere Reduktionswirkung.
14
125 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,25 μT ändert
Peter Unterwieser
Seite 74
µT
90
10,0
75
95
85
85
11,0
95
%
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
12,0
MFCALC Railway Version Sbb.1.0
13,0
90
Reduktionsfaktorenrechnung mit MF-Calc-railway
6.5 Reduktionswirkung der Längsbanderder
Die in Abschnitt 6.2 beschriebene Reduktionswirkung für einen gesamten Tunnel mit 32
Armierungsleitern stellt den besten praktischen Fall dar. Die Reduktionswirkung der
Längsbanderder ist, weil sie den Schienen so nahe sind, am geringsten.
Da an den Trennstellen des Tunnels die Armierung nicht durchgehend ist sondern nur
durchverbunden ist, muss diese Stelle separat untersucht werden. An diesen Stellen ist die
Reduktionswirkung am kleinsten, weil dort die wenigsten Armierungsleiter vorhanden sind.
Die Breite einer Trennstelle beträgt in der Praxis ungefähr 10 bis 40 cm. Durch diese kurze
Tennstelle kommt es zu Randerscheinungen im magnetischen Feldverlauf. Da die
Homogenität aber Vorrausetzung für die Richtigkeit der Simulation mit MF-Calc-railway ist,
können deshalb nur die maximalen Felder abgeschätzt werden. Das bedeutet, aus der
Simulation folgt nur eine Abschätzung der minimalen Reduktionswirkung. In Wirklichkeit ist
die zu erwartende Reduktionswirkung größer. Man kann sagen, die tatsächliche
Reduktionswirkung für die Blockfuge liegt irgendwo zwischen der in (Abbildung 6.16)
dargestellten
minimalen
und
der
in
(Abbildung
6.5)
dargestellten
maximalen
Reduktionswirkung.
Es wird die magnetische Ersatzflussdichte mit und ohne Armierungsleiter verglichen. Ein
Längsbanderder aus Bandstahl mit 40 mm x 4 mm ergibt einen Querschnitt von 160 mm2.
Peter Unterwieser
Seite 75
Reduktionsfaktorenrechnung mit MF-Calc-railway
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
13,0
12,0
11,0
10,0
9,0
8,0
Y
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
15,0
14,0
13,0
12,0
11,0
9,0
10,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
X
TU-Graz
A.Abart 2003
Abbildung 6.15 : Leiteranordnung mit Längsbanderdern in MF-Calc-railway
Abgebildet ist die aus dem Grüntunnel bekannte Leiteranordnung (siehe Abbildung 5.4) mit
den zwei in Grün gezeichneten Längsbanderdern. Die rot dargestellten Leiter knapp über den
Längsbanderdern bilden den Handlauf nach. Diese Anordnung wird wieder mit der
Anordnung ohne Armierungsleiter in Abbildung 6.1 verglichen.
Es kann nun wieder die relative Änderung gebildet und in einem Differenzfeldbild dargestellt
werden.
Peter Unterwieser
Seite 76
Reduktionsfaktorenrechnung mit MF-Calc-railway
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
11,0
10,0
9,0
100
8,0
Y
7,0
100
6,0
5,0
110
4,0
110
110
2,0
0,0
110
100
110
1,0
-1,0
120
X
15,0
14,0
13,0
12,0
11,0
9,0
10,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-2,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
110
100
100
110
-15,0
3,0
110
TU-Graz
A.Abart 2003
Abbildung 6.16 : Relative Änderung der EFD in %15
Es ist genau zu erkennen, dass im Nahbereich der Banderder eine Zunahme der EFD auftritt.
Die Reduktionswirkung der Abbildung 6.16 beträgt 102,7 %! Das bedeutet der
flächenbezogene Verlauf der EFD erhöht seinen Wert unter Einfluss der Längsbanderder.
Interessant ist nun der Fernbereich, welcher in einem größeren Ausschnitt dargestellt wird.
15
102,7 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,027 μT ändert
Peter Unterwieser
Seite 77
%
110
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
µT
12,0
MFCALC Railway Version Sbb.1.0
13,0
76,0
70,0
64,0
58,0
52,0
46,0
40,0
34,0
28,0
100
22,0
16,0
10,0
4,0100
110
-2,0
-8,0
-14,0
-20,0
-26,0
-32,0
-38,0
-44,0
-50,0
-56,0
-62,0
-68,0
-74,0
-80,0
95
100
100
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
X
TU-Graz
A.Abart 2003
Abbildung 6.17 : Relative Änderung der EFD in %16 als großer Ausschnitt
In dieser Abbildung ist eine geringe Verbesserung gegenüber dem kleinen Ausschnitt zu
erkennen. Die Reduktionswirkung der Abbildung 6.17 beträgt 97,16 %.
16
125 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,25 μT ändert
Peter Unterwieser
Seite 78
%
78,0
74,0
70,0
66,0
62,0
58,0
54,0
50,0
46,0
42,0
38,0
34,0
30,0
26,0
22,0
18,0
14,0
10,0
6,0
2,0
-2,0
µT
Gleis1
500A 0°
GR2
MFCALC Railway Version Sbb.1.0
Gleis0
0A 0°
GR1
Y
Reduktionsfaktorenrechnung mit MF-Calc-railway
Reduktionsfaktorenrechnung mit MF-Calc-railway
6.6 Optimale geometrische Auslegung der Tunnelarmierung
Die Frage ist, wie könnte eine sinnvolle Anordnung der Armierungsleiter aussehen. Das Ziel
ist, mit möglichst wenigen Armierungsleitern eine möglichst hohe Reduktionswirkung zu
erzielen. Diese Aufgabe stellt sich einerseits für die Blockfuge, die die Trennstelle der
einzelnen Abschnitte ist. Andererseits ganz allgemein für die Frage, ob Stahlbeton verwendet
werden soll oder nicht.
Als Maximum ist 150 % gewählt, um die Darstellungen wie vorher optimal miteinander
vergleichen zu können. Als Versuchsanordnung dient wieder die aus dem Grüntunnel
bekannte Leiteranordnung.
Es soll ermittelt werden, wie die Tunnelleiter räumlich optimal angeordnet werden, um eine
maximale Feldreduktionswirkung bei möglichst geringer Anzahl von Armierungsleitern zu
erhalten. Die Idee dabei ist, die Tunnelleiter möglichst nahe an die traktionsstromführenden
Leiter zu legen.
Als erstes sollen 2 Leiter in die Lücke zwischen Rückleiter und Verstärkungsleitung gelegt
werden. Wir können die Leiter nur im Schnittbereich des Tunnels anordnen, weil sie Teil des
Stahlbetons sind.
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
13,0
12,0
11,0
10,0
9,0
8,0
Y
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
X
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
-2,0
TU-Graz
A.Abart 2003
Abbildung 6.18 : Leiteranordnung mit 2 Armierungleitern
Peter Unterwieser
Seite 79
Reduktionsfaktorenrechnung mit MF-Calc-railway
Dargestellt ist die prinzipielle Anordnung der zwei Gleissysteme mit zwei Armierungleitern.
15,0
Gleis1
500A 0°
GR2
14,0
85
11,0
85
10,0
9,0
90
80
90
7,0
110
95
Y
80
85
8,0
75
85
90
5,0
95
75
6,0
85
4,0
3,0
90
75
2,0
1,0
0,0
85
X
15,0
14,0
13,0
12,0
11,0
9,0
10,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
80
-1,0
TU-Graz
A.Abart 2003
Abbildung 6.19 : Relative Änderung der EFD in %17
In der Abbildung 6.19 ist deutliche Verbesserung im Vergleich zur Abbildung 6.16 zu
erkennen. Der flächenbezogene Ersatzflussdichtereduktionsfaktor der Abbildung 6.19 beträgt
83,47 %.
Dieselbe Anordnung wird für den Fernbereich in einem größeren Ausschnitt dargestellt.
17
125 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,25 μT ändert
Peter Unterwieser
Seite 80
%
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
12,0
µT
13,0
85
MFCALC Railway Version Sbb.1.0
Gleis0
0A 0°
GR1
76,0
70,0
64,0
58,0
52,0
46,0
40,0
34,0
28,0
22,0
16,0
10,0
4,0
-2,0
80
X
TU-Graz
A.Abart 2003
Abbildung 6.20 : Relative Änderung der EFD in %18 als großer Ausschnitt
Der flächenbezogene Ersatzflussdichtereduktionsfaktor der Abbildung 6.20 beträgt 80,73 %.
Als nächstes sollen 2 Leiter genau über die Verstärkungsleitungen gelegt werden, um deren
Einfluss durch einen geringen Abstand zu optimieren. Die Verstärkungsleitungen führen
ungefähr den halben Traktionsstrom und erzeugen somit mindestens das halbe magnetische
Feld der Anordnung. Diese Annahme der Stromverteilung ist dem Reportblatt von MF-Calcrailway zu entnehmen. Im Reportblatt wird die errechnete Stromverteilung aller Leiter
eingetragen.
18
125 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,25 μT ändert
Peter Unterwieser
Seite 81
µT
80
-8,0
-14,0
-20,0
-26,0
-32,0
-38,0
-44,0
-50,0
-56,0
-62,0
-68,0
-74,0
-80,0
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
%
78,0
74,0
70,0
66,0
62,0
58,0
54,0
50,0
46,0
42,0
38,0
34,0
30,0
26,0
22,0
18,0
14,0
10,0
6,0
2,0
-2,0
MFCALC Railway Version Sbb.1.0
Gleis1
500A 0°
GR2
80
Gleis0
0A 0°
GR1
Y
Reduktionsfaktorenrechnung mit MF-Calc-railway
Reduktionsfaktorenrechnung mit MF-Calc-railway
Gleis0
0A 0°
GR1
15,0
Gleis1
500A 0°
GR2
14,0
9,0
85
8,0
100
85
95
6,0
90
90
95
5,0
85
4,0
3,0
90
75
2,0
85
85
75
1,0
0,0
85
%
70
Y
7,0
µT
85
75
10,0
MFCALC Railway Version Sbb.1.0
11,0
80
75
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
µT
12,0
MFCALC Railway Version Sbb.1.0
13,0
15,0
14,0
13,0
12,0
11,0
9,0
10,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
80
-1,0
TU-Graz
A.Abart 2003
X
Abbildung 6.21 : Relative Änderung der EFD in %19
Gleis1
500A 0°
GR2
80
80
76,0
70,0
64,0
58,0
52,0
46,0
40,0
34,0
28,0
22,0
85
16,0
10,0
4,0
75
-2,0
-8,0
-14,0
-20,0
-26,0
-32,0
-38,0
-44,0
-50,0
-56,0
-62,0
-68,0
-74,0
-80,0
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
X
TU-Graz
A.Abart 2003
Abbildung 6.22 : Relative Änderung der EFD in %20 als großer Ausschnitt
Der flächenbezogene Ersatzflussdichtereduktionsfaktor der Abbildung 6.22 beträgt 79,50 %.
19
125 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,25 μT ändert
20
125 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,25 μT ändert
Peter Unterwieser
Seite 82
%
78,0
74,0
70,0
66,0
62,0
58,0
54,0
50,0
46,0
42,0
38,0
34,0
30,0
26,0
22,0
18,0
14,0
10,0
6,0
2,0
-2,0
80
Gleis0
0A 0°
GR1
Y
Der flächenbezogene Ersatzflussdichtereduktionsfaktor der Abbildung 6.21 beträgt 81,60 %.
Reduktionsfaktorenrechnung mit MF-Calc-railway
Der nächste Schritt ist es, die beiden vorherigen Fälle zu kombinieren. Das bedeutet zweimal
zwei Armierungsleiter zu verwenden.
15,0
14,0
70
70
13,0
70
11,0
75
10,0
70
60
80
9,0
65
7,0
Y
60
70
8,0
75
95
6,0
55
5,0
90
4,0
80
85
3,0
75
70
2,0
75
80
1,0
75
0,0
70
X
15,0
14,0
13,0
12,0
11,0
9,0
10,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
-12,0
-13,0
-14,0
-15,0
65
60
-1,0
TU-Graz
A.Abart 2003
Abbildung 6.23 : Relative Änderung der EFD in %21
Der flächenbezogene Ersatzflussdichtereduktionsfaktor der Abbildung 6.23 beträgt 70,06 %.
In dieser relativen Abbildung ist der flächenbezogene Ersatzflussdichtereduktionsfaktor nicht
ganz die Summe der beiden vorhergehenden Anordnungen mit zwei Leitern.
In der Praxis kann man die Position der Armierungsleiter nicht vorgeben, da der gesamte
Stahlbeton mit dem Armierungsgeflecht durchzogen ist. Daraus folgt, dass insbesondere der
Bereich des oberen Bogens, der die Rückströme führt, die magnetischen Felder reduziert.
Man erkennt, dass bei einer Ummantelung der traktionsstromführenden Leiter eine optimale
Reduktionswirkung mit geringem Aufwand erzielt werden kann. Der Grund dafür liegt im
geringen Abstand von Hin- und Rückleiter und der damit verbunden großen Koppelimpedanz.
Auch für die Trennstellen stellt diese Anordnung eine ideale Lösung dar. Das heißt die
Trennstellen sollten in Bereich des oberen Bogens durchverbunden werden.
21
125 % relative Änderung bedeutet, dass sich die EFD von 1 μT auf 1,25 μT ändert
Peter Unterwieser
Seite 83
%
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
12,0
60
µT
Gleis1
500A 0°
GR2
70
MFCALC Railway Version Sbb.1.0
Gleis0
0A 0°
GR1
70
Reduktionsfaktorenrechnung mit MF-Calc-railway
6.7 Gedanken zur optimalen geometrischen Reduktionsleiteranordnung
Wie könnte die magnetfeldoptimale elektrische Eisenbahn aussehen, wenn man nicht auf die
praktische Ausführbarkeit achtet?
Die optimale Anordnung stellt die aus der Praxis bekannte Koaxialgeometrie mit dem
traktionsstromführenden Leiter in der Mitte, der von dem Rückleiter umgeben ist, dar.
Skizze zur allgemeinen Leiteranordnung:
Abbildung 6.24 : Allgemeine Leiteranordnung
In der Mitte ist der Fahrdraht der den feldverursachenden Leiter darstellt. Darunter sind die
Schienen die die Rückleiter darstellen. In Rot ist der konzentrische Kreis mit dem Fahrdraht
als Mittelpunkt unter Einbeziehung der Schienen auf dem Radius dargestellt.
Peter Unterwieser
Seite 84
Reduktionsfaktorenrechnung mit MF-Calc-railway
Abbildung 6.25 : Leiteranordnung mit Abständen der Reduktionsleiter
Es werden nur die Reduktionsleiter auf einem Kreis mit der Oberleitung als Mittelpunkt
angeordnet. Die Reduktionsleiter werden in einem Winkel zueinander von je 10 Grad
zueinander positioniert. So wird der ganze Kreis mit Reduktionsleitern besetzt.
Peter Unterwieser
Seite 85
Reduktionsfaktorenrechnung mit MF-Calc-railway
Abbildung 6.26 : Vollständige Leiternanordnung
Die in Abbildung 6.26 dargestellten Leiter werden nun in MF-Calc-railway eingegeben und
die EFD berechnet. Dies geschieht einmal mit und einmal ohne Reduktionsleiter.
Anschließend wird die relative Differenz gebildet und graphisch dargestellt.
Peter Unterwieser
Seite 86
20,0
19,0
18,0
17,0
16,0
15,0
14,0
13,0
12,0
11,0
10,0
9,0
8,0
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
20,0
18,0
16,0
14,0
12,0
10,0
8,0
6,0
4,0
2,0
0,0
-2,0
-4,0
-6,0
-8,0
-10,0
-12,0
-14,0
-16,0
-18,0
-20,0
Gleis0
500A 0°
GR1
Y
Reduktionsfaktorenrechnung mit MF-Calc-railway
TU-Graz
A.Abart 2003
X
Abbildung 6.27 : Vollständige Leiteranordnung in MF-Calc-railway
Die Abbildung 6.27 stellt die eingegeben Leiter mit Reduktionsleiter dar. Als Strom im
1
2
4
4
38,0
35,0
32,0
29,0
26,0
23,0
20,0
17,0
14,0
11,0
8,0
5,0
2,0
-1,0
-4,0
-7,0
-10,0
-13,0
-16,0
-19,0
-22,0
-25,0
-28,0
-31,0
-34,0
-37,0
-40,0
1
1
2
1
20
20
10
10
5
40,0
38,0
36,0
34,0
32,0
30,0
28,0
26,0
24,0
22,0
20,0
18,0
16,0
14,0
12,0
10,0
8,0
6,0
4,0
2,0
0,0
-2,0
-4,0
-6,0
-8,0
-10,0
> 500
< 500
< 400
< 300
< 200
< 100
< 50
< 40
< 30
< 20
< 10
< 5
< 4
< 3
< 2
< 1
< 0.5
< 0.4
< 0.3
< 0.2
< 0.1
< 0.05
< 0.04
< 0.03
< 0.02
< 0.01
< 0.005
< 0.004
< 0.003
< 0.002
< 0.001
TU-Graz
A.Abart 2003
X
Abbildung 6.28 : EFD-Verteilung der Leiteranordnung
Peter Unterwieser
Seite 87
µT
3
3
2
2
1
1
Gleis0
500A 0°
GR1
Y
Fahrdraht wurde 500 A gewählt.
Reduktionsfaktorenrechnung mit MF-Calc-railway
> 500
< 500
< 400
< 300
< 200
< 100
< 50
< 40
< 30
< 20
< 10
< 5
< 4
< 3
< 2
< 1
< 0.5
< 0.4
< 0.3
< 0.2
< 0.1
< 0.05
< 0.04
< 0.03
< 0.02
< 0.01
< 0.005
< 0.004
< 0.003
< 0.002
< 0.001
TU-Graz
A.Abart 2003
X
Abbildung 6.29 : EFD-Verteilung der Leiteranordnung mit Reduktionsleitern
Man erkennt am Bild der EFD-Verteilung in Abbildung 6.28 eine deutliche Feldreduktion im
Vergleich zur Abbildung 6.29.
Peter Unterwieser
Seite 88
µT
40,0
38,0
36,0
34,0
32,0
30,0
28,0
26,0
24,0
22,0
20,0
18,0
16,0
14,0
12,0
10,0
8,0
6,0
4,0
2,0
0,0
-2,0
-4,0
-6,0
-8,0
-10,0
38,0
35,0
32,0
29,0
26,0
23,0
20,0
17,0
14,0
11,0
8,0
5,0
2,0
-1,0
-4,0
-7,0
-10,0
-13,0
-16,0
-19,0
-22,0
-25,0
-28,0
-31,0
-34,0
-37,0
-40,0
0.1
0.1
0.2
0.2
0.4
0.4
0.3
0.3
50
0.3
0.3
0.2
0.2
0.1
Gleis0
500A 0°
GR1
Y
Die Abbildung 6.28 stellt die räumliche EFD-Verteilung der Leiteranordnung dar.
Reduktionsfaktorenrechnung mit MF-Calc-railway
Es wird die relative Änderung gebildet und graphisch dargestellt. Als Maximalwert der Skala
10
38,0
35,0
32,0
29,0
26,0
23,0
20,0
17,0
14,0
8,0
11,0
5,0
2,0
-1,0
-4,0
-7,0
-10,0
-13,0
-16,0
-19,0
-22,0
-25,0
-28,0
-31,0
-34,0
-37,0
-40,0
10
10
10
> 150
< 150
< 145
< 140
< 135
< 130
< 125
< 120
< 115
< 110
< 105
< 100
< 95
< 90
< 85
< 80
< 75
< 70
< 65
< 60
< 55
< 50
< 45
< 40
< 35
< 30
< 25
< 20
< 15
< 10
< 5
TU-Graz
A.Abart 2003
X
Abbildung 6.30 : Relative Änderung
Die EFD reduziert sich auf bis zu 10 % der ursprünglichen EFD. Der flächenbezogene
Ersatzflussdichtereduktionsfaktor für die Abbildung 6.30 beträgt 12,78 %.
Auswertung der Ergebnisse:
Die koaxiale Anordnung von Oberleitung und Reduktionsleitern stellt die aus der Praxis
bekannte theoretisch optimale Lösung zur Reduktion der Felder dar. Warum sie sich bei
elektrischen Eisenbahnen wahrscheinlich nicht durchsetzen wird hat mehrere Gründe:
Die koaxiale Geometrie würde für eine zweigleisige Strecke zwei Reduktionsleiterkreise
erfordern. Es wären neue Maste mit kreisförmiger Gestalt nötig. Ein Tunnel müsste in
entsprechender Weise größer gebaut werden. Die Kosten für die Errichtung solcher Anlagen
wären nicht wirtschaftlich. Die erzielbaren Reduktionswirkungen stehen in keiner Relation zu
den Aufwendungen. Trotz all dieser praktischen Einschränkungen weist diese koaxiale
Anordnung doch die ideale Reduktion auf.
Peter Unterwieser
Seite 89
µT
10
10
%
40,0
38,0
36,0
34,0
32,0
30,0
28,0
26,0
24,0
22,0
20,0
18,0
16,0
14,0
12,0
10,0
8,0
6,0
4,0
2,0
0,0
-2,0
-4,0
-6,0
-8,0
-10,0
Gleis0
500A 0°
10
GR1
Y
ist 150 % gewählt.
Reduktionsfaktorenrechnung mit MF-Calc-railway
Da die Berechnungsverfahren auf den in der Ferne aufgenommenen Traktionsstrom aufbauen
stellt sich nun die Frage wie die Flussdichtenverteilung aussieht, wenn der Traktionsstrom
unmittelbar im Bereich des Beobachtungspunkts aufgenommen wird. Systembedingt wird der
vom Fahrdraht aufgenommene Fahrstrom über die Schienen, oder zumindest eine Schiene
zurück und in das Erdreich geleitet. Erst über die Länge kann sich dann der Rückstrom
gleichmäßig auf eine elektrisch und geometrisch radialsymmetrische Anordnung von
Rückleitern aufteilen. Das bedeutet, dass durch dieses Verfahren Spitzenwerte der Flussdichte
nicht bzw. nur wenig reduziert werden könnten, außer es werden von der Lokomotive
ausgehende radialsymmetrische Schleifkontakte gebildet. Dass diese Lösung wohl im Reich
der technischen Phantasie beheimatet ist zeigt folgende Abbildung.
Peter Unterwieser
Seite 90
Zusammenfassung und Ergebnisse
7 Zusammenfassung und Ergebnisse
Im Rahmen dieser Arbeit werden niederfrequente magnetische Felder, die bei elektrischen
Eisenbahnen unter Einfluss von Reduktionsleitern auftreten, gemessen, berechnet und
analysiert. Das Auftreten einer reduzierenden Wirkung wird für verschiedene Anordnungen in
Theorie und Praxis untersucht. Die von den stromführenden Leitern verursachten
magnetischen Flussdichten werden mittels Modellen berechnet, interpretiert und graphisch
dargestellt.
Am Beginn der Arbeit werden Grundlagen über Entstehung, Messung und Berechnung
magnetischer Wechselfelder erläutert. Es werden die magnetische Ersatzflussdichte und
Profile der magnetischen Flussdichte aus den Vektorkomponenten der magnetischen
Flussdichte berechnet. Die Berechnung wird anhand eines Modells für ein ebenes Problem für
den homopolaren stromdurchflossenen Leiter sowie für den Hin- und Rückleiter mit dem
Programm MF-Calc-railway nach Carson & Polaczek und Biot-Savart durchgeführt. Zum
Ausdruck kommt hierbei die feldreduzierende Wirkung der Hin- und Rückleitung bei
entsprechender räumlicher Nähe beider Leiter.
Weiters wird anhand eines kurzen Rechenbeispieles die Arbeitsweise des Programms MFCalc-railway erklärt. Dazu wird eine Anordnung von zwei Leitern zuerst analytisch und dann
mit MF-Calc-railway gerechnet und die Übereinstimmung demonstriert.
Mit Hilfe einer Messung der magnetischen Felder beim Grüntunnel (an der Westbahnstrecke
in Niederösterreich) konnten die grundsätzlichen Verläufe der Ersatzflussdichte der
Simulation bestätigt werden. Es wurde ein 2-Sonden-Messverfahren eingesetzt um, trotz der
Zeitvarianz der magnetischen Felder, eine vernünftige Messung durchführen zu können.
Bestehende wesentliche Abweichungen zwischen Mess- und Berechnungsergebnissen lassen
auf vom Modell abweichende reale Bedingungen schließen.
Zur besseren Übersichtlichkeit wurde eine geeignete Darstellung zur Visualisierung der
Änderung erarbeitet. Sie stellt die Differenz der örtlich veränderlichen Feldverhältnisse von
zwei verschiedenen Feldbildern in Falschfarbendarstellung dar. Erst mit dieser Visualisierung
wurde es möglich, die örtlichen Veränderungen der Feldverhältnisse zu vergleichen und die
Reduktionswirkung zu beurteilen.
Untersucht wurden der Einfluss der Tunnelarmierung und der Einfluss der Rückleiterführung
auf der freien Strecke auf die magnetischen Felder. Abschließend wurde noch eine optimierte
Form der Tunnelarmierung erarbeitet.
Peter Unterwieser
Seite 91
Zusammenfassung und Ergebnisse
Es konnte gezeigt werden, dass die magnetische Ersatzflussdichte bei zwei Leitern um
17,5 %, bei vier Leitern um 30 % und beim idealen Tunnel um 87,3 % gesenkt werden kann.
Weiter ist zu erkennen, dass es zwei grundlegende Einflussfaktoren gibt, einerseits der
Abstand und die räumliche Lage des Rückleiters zu traktionsstromführenden Leitern und
damit die Größe des reduzierenden Feldes und anderseits der elektrische Widerstand der
Reduktionsleiter, der die Stromverteilung der Anordnung bestimmt. Es stellt sich natürlich die
Frage nach der Qualität des Modells hinsichtlich realer Verhältnisse. Im Speziellen konnten
die Impedanzverhältnisse der Anordnung für die Simulation nur abgeschätzt werden und die
elektrischen Eigenschaften einer Tunnelauskleidung wurden, als über den Querschnitt
homogen angenommen. Die Prozentangaben in den Differenzdarstellungen sind daher
gegenüber realen Verhältnissen mit der Unsicherheit des Modells behaftet.
Dennoch zeigt diese Arbeit den Einfluss von Kompensationsleitern auf die Ersatzflussdichte
in der Umgebung von elektrischen Eisenbahnen, und bietet Ansätze, die es gestatten die
elektromagnetischen Emissionen zu minimieren. Dabei zeigt sich unter anderem, dass
vollständig optimierte Systeme weitab von technisch sinnvoll realisierbaren Lösungen liegen.
Peter Unterwieser
Seite 92
Formelzeichen und Abkürzungen
8 Formelzeichen und Abkürzungen
Konstanten
π
Pi
3,14159
[1]
ε0
Dielektrizitätskonstante
8,854 ·10-12
[As/Vm]
μ0
Permeabilitätskonstante
4π
·10-7
[Vs/Am]
Variablen
x,y,z
Koordinaten des Raumes
[m]
t
Zeit
[s]
f
Frequenz
[Hz]
ω
Kreisfrequenz
[1/s]
I
elektrische Stromstärke
[A]
U
r
E
r
H
r
B
elektrische Spannung
[V]
Vektor der elektrischen Feldstärke
[V/m]
Vektor der magnetische Feldstärke
[A/m]
Vektor der magnetischen Flussdichte
[T]
Φ
r
J
magnetischer Fluss
[ Wb ]
Vektor der Stromdichte
[A/m2]
N
Windungszahl der Induktionsspule
[1]
Uind
induzierte Spannung
[V]
ϕ
Phasenverschiebung der induzierten Spannung
[1]
Vektor eines Linienelementes
[m]
Vektor eines Linienelementes
[m]
Vektor des Radius
[m]
r
ds
r
dl
r
r
Peter Unterwieser
Seite 93
Formelzeichen und Abkürzungen
Formelzeichen
∂
∂t
partielle Ableitung nach der Zeit
div
r ∂B
∂B
∂B
Divergenz divB = x + y + z
∂z
∂x
∂y
rot
Rotor
⎛∂ ⎞
⎜ ⎟
⎜ ∂x ⎟ ⎛ B ⎞
r ⎜ ∂ ⎟ ⎜ x⎟
× B
rotB =
⎜ ∂y ⎟ ⎜ y ⎟
⎜ ∂ ⎟ ⎜⎝ Bz ⎟⎠
⎜ ⎟
⎝ ∂z ⎠
Abkürzungen
ÖBB
Österreichische Bundesbahnen
RL
Rückleiter
ELF
Extremely Low Frequency
UW
Umspannwerk
mag.
magnetisch
bez.
bezogen
FD3
Messgerätetype der Firma Combinova
EFA3
Messgerätetype der Firma Wandel & Goltermann
MF-Calc-railway
Softwarepaket zur Berechnung von magnetischen Feldern in der
Umgebung von elektrischen Eisenbahnen
2D
2 dimensional
3D
3 dimensional
Peter Unterwieser
Seite 94
Abbildungsverzeichnis
9 Abbildungsverzeichnis
Abbildung 1.1 : Grüntunnel bei St.Pöllten................................................................................. 2
Abbildung 2.1 : Feldbild eines geraden einfachen Leiters......................................................... 8
Abbildung 2.2 : Stromfaden in Z-Richtung von –l/2 bis +l/2 .................................................... 9
Abbildung 2.3 : Magnetisches Vektorfeld im Aufpunkt A(X, Y, Z) ....................................... 12
Abbildung 2.4 : Messprinzip für die mag. Flussdichte unter Berücksichtigung der................ 17
Abbildung 2.5 : Combinova-FD3 mit Skizze der Spulenachsen ............................................. 19
Abbildung 2.6 : Achsen und Frontansicht des Magnetfeldmessgerätes EFA-3....................... 23
Abbildung 3.1 : Magnetische EFD einer zweigleisigen Bahnanlage unter Einfluss eines
Tunnels ............................................................................................................................. 28
Abbildung 3.2 : Eingabeoberfläche des Tunnels aus MF-Calc-railway .................................. 29
Abbildung 3.3 : Eingabeoberfläche des Tunnels für die charakteristischen Daten ................. 30
Abbildung 3.4 : Änderungsoberfläche des Tunnelmoduls aus MF-Calc-railway.................... 31
Abbildung 3.5 : MF-Calc-railway beim Berechnungsvorgang................................................ 32
Abbildung 3.6 : MF-Calc-railway mit dem Berechnungsergebnis .......................................... 33
Abbildung 4.1 : Anordnung der Leiter und des Aufpunkts...................................................... 36
Abbildung 4.2 : Abstände der Leiter mit Bemaßung ............................................................... 36
Abbildung 4.3 : Feldbild der Leiters 1 ..................................................................................... 37
Abbildung 4.4 : Feldbild der Leiters 2 ..................................................................................... 38
Abbildung 4.5 : Feldsuperposition für die Leiter 1 und 2........................................................ 39
Abbildung 4.6 : Auszug aus dem Reportblatt (MF-Calc-railway)........................................... 40
Abbildung 4.7 : Anordnung der Leiter..................................................................................... 41
Abbildung 4.8 : Feldbild der Ersatzflußdichte ......................................................................... 42
Abbildung 4.9 : Diagramm der mag. Ersatzflußdichte in der Aufpunktsebene ....................... 42
Abbildung 4.10 : Auszug aus dem Profildatenblatt ................................................................. 43
Abbildung 4.11 : Auszug aus dem Ergebnisblatt..................................................................... 43
Abbildung 5.1 : Bild vom Grüntunnel Blickrichtung Osten .................................................... 44
Abbildung 5.2 : Skizze des Messvorganges............................................................................. 46
Abbildung 5.3 : Oberleitungsstrom in Abhängigkeit der Zeit ................................................. 47
Abbildung 5.4 : Skizze des Grüntunnels mit allen Leitern ...................................................... 49
Abbildung 5.5 : Angenommene Position der Tunnelleiter ...................................................... 50
Abbildung 5.6 : Daten für die Simulation ................................................................................ 50
Peter Unterwieser
Seite 95
Abbildungsverzeichnis
Abbildung 5.7 : Magnetische Felder einer zweigleisigen Bahnanlage unter Einfluss eines
Tunnels ............................................................................................................................. 53
Abbildung 5.8 : Magnetische Ersatzflußdichte einer zweigleisigen Bahnanlage bei einem
Tunnel in der Höhe von ca. 10 m über der Sohlplatte des Tunnels ................................. 54
Abbildung 5.9 : Bezogene magnetische Ersatzflußdichte einer zweigleisigen Bahnanlage
in einem Tunnel in der Höhe von ca. 10 m über der Gleisebene des Tunnels
(Messung M1 quer) .......................................................................................................... 55
Abbildung 5.10: Magnetische Ersatzflußdichte einer zweigleisigen Bahnanlage bei einem
Tunnel in der Höhe von ca. 10 m über der Sohlplatte des Tunnels. ................................ 56
Abbildung 5.11 : Vergleich der Rechnung und der Messung der bezogenen mag.
Flussdichte in X Richtung einer zweigleisigen Bahnanlage in einem Tunnel in der
Höhe von ca. 10 m über der Sohlplatte des Tunnels (Messung M1 quer). ...................... 57
Abbildung 5.12. : Vergleich der Rechnung und der Messung der bezogenen mag.
Flussdichte in Y Richtung einer zweigleisigen Bahnanlage in einem Tunnel in der
Höhe von ca. 10 m über der Sohlplatte des Tunnels (Messung M1 quer) ....................... 57
Abbildung 5.13 : Vergleich der Rechnung und der Messung der bezogenen mag.
Ersatzflußdichte einer zweigleisigen Bahnanlage in einem Tunnel in der Höhe von
ca. 10 m über der Sohlplatte des Tunnels (Messung M1 quer)........................................ 58
Abbildung 5.14 : Ergebnisse der Messung der bezogenen mag. Ersatzflußdichte der festen
und der mobilen Sonde einer zweigleisigen Bahnanlage in einem Tunnel in der Höhe
von ca. 10 m über der Sohlplatte des Tunnels (Messung M1 quer)................................. 59
Abbildung 6.1 : Leiteranordnung ohne Armierungsleiter in MF-Calc-railway ....................... 63
Abbildung 6.2 : EFD der Anordnung ohne Armierungsleiter.................................................. 64
Abbildung 6.3 : Leiteranordnung mit Tunnelleitern in MF-Calc-railway ............................... 64
Abbildung 6.4 : EFD der Anordnung mit Tunnelleiter............................................................ 65
Abbildung 6.5 : Relative Änderung der EFD in % .................................................................. 65
Abbildung 6.6 : EFD der Anordnung ohne Armierungsleiter als großer Ausschnitt............... 67
Abbildung 6.7 : EFD der Anordnung mit Armierungsleiter als großer Ausschnitt ................. 67
Abbildung 6.8 : Relative Änderung der EFD in % als großer Ausschnitt ............................... 68
Abbildung 6.9 : Abhängigkeit der relativen Änderung der EFD von der Anzahl der
Armierungsleiter............................................................................................................... 69
Abbildung 6.10 : Abhängigkeit der relativen Änderung der EFD vom Widerstandsbelag
der Armierungsleiter ........................................................................................................ 70
Abbildung 6.11 : Einfluss der Zahl der Tunnelleiter auf die relative Änderung ..................... 71
Peter Unterwieser
Seite 96
Abbildungsverzeichnis
Abbildung 6.12 : Standardanordnung der freien Strecke ohne Rückleiter .............................. 72
Abbildung 6.13 : Standardanordnung der freien Strecke mit Rückleiter ................................. 73
Abbildung 6.14 : Relative Änderung der EFD in % mit und ohne RL .................................... 74
Abbildung 6.15 : Leiteranordnung mit Längsbanderdern in MF-Calc-railway ....................... 76
Abbildung 6.16 : Relative Änderung der EFD in % ................................................................ 77
Abbildung 6.17 : Relative Änderung der EFD in % als großer Ausschnitt ............................. 78
Abbildung 6.18 : Leiteranordnung mit 2 Armierungleitern..................................................... 79
Abbildung 6.19 : Relative Änderung der EFD in % ................................................................ 80
Abbildung 6.20 : Relative Änderung der EFD in % als großer Ausschnitt ............................. 81
Abbildung 6.21 : Relative Änderung der EFD in % ................................................................ 82
Abbildung 6.22 : Relative Änderung der EFD in % als großer Ausschnitt ............................. 82
Abbildung 6.23 : Relative Änderung der EFD in % ................................................................ 83
Abbildung 6.24 : Allgemeine Leiteranordnung ....................................................................... 84
Abbildung 6.25 : Leiteranordnung mit Abständen der Reduktionsleiter ................................. 85
Abbildung 6.26 : Vollständige Leiternanordnung.................................................................... 86
Abbildung 6.27 : Vollständige Leiteranordnung in MF-Calc-railway..................................... 87
Abbildung 6.28 : EFD-Verteilung der Leiteranordnung.......................................................... 87
Abbildung 6.29 : EFD-Verteilung der Leiteranordnung mit Reduktionsleitern ...................... 88
Abbildung 6.30 : Relative Änderung ....................................................................................... 89
Peter Unterwieser
Seite 97
Literaturnachweis
10 Literaturnachweis
[1] BEMS 22th Annual Meeting 2000 Munich Abstract Book BEMS 2000
[2] Larch, J.: Niederfrequente magnetische Drehfelder in der elektrischen Energietechnik
[3] Biro, O.: Vorlesungsskriptum Theorie der Elektrotechnik 2. TU Graz, Institut IGTE. 2001.
[4] Abart, A.: Visualisierung der 50 Hz Magnetfelder im Haushalt und in öffentlichen
Bereichen. TU Graz, Institut für Elektrische Anlagen.
[5] Kunsch B., Neubauer G., Garn H., Bonek E., Leitgeb N., Magerl G., Jahn O.: Studie
dokumentierter Forschungsresultate über Wirkung elektromagnetischer Felder Teil 1;
Bundesministerium für Gesundheit und Konsumentenschutz, 1997.
[6] Abart, A.: Diplomarbeit. TU Graz, Institut für Elektrische Anlagen. 1997.
[7] Bedienungsanleitung Combinova-FD3
[8] Bedienungsanleitung EFA-1/EFA-2/EFA-3EM-Feldanalysator B-Feld. BN 2245/98.01
[9] Abart, A.: Auszüge aus Programmbeschreibung und Bedienungsanleitung
MF-Calc-railway. TU Graz, Institut für Elektrische Anlagen.
[10] Friedrich, W.: Tabellenbuch Elektrotechnik Elektronik. ISBN 3-427-53024-8, Dümmlers
Verlag, 1993.
[11] Weinmann, A .: ELIN Formeln und Fakten. ISBN 3-9500084-0-3, Firma ELIN, 1991.
Peter Unterwieser
Seite 98