Formelsammlung zur LV „Mathematik“

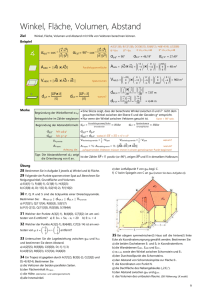
Prof. U. Stephan
TFH Berlin, FB II
Studiengang BAU – 1. Fachsemester
LV „Mathematik“
Übung 1
Seite 1 von 5
Hinweise:
• Erstellen Sie in den Fällen, wo die Aufgabe keine Skizze enthält, erst eine Skizze.
• Benutzen Sie die in der Aufgabe gegebenen Bezeichnungen.
• Für fehlende Bezeichnungen überlegen Sie sich selbst einen Platzhalter.
• Längen sind jeweils mit Einheiten anzugeben, gerechnet auf 1 mm Genauigkeit (wie Sie später ein solches berechnetes Ergebnis in die Baupraxis übertragen, ist Ihre Sache).
• Berechnete Winkel sind auf eine Stelle nach dem Komma zu runden.
• Alle Rechnungen werden komplett in voller Genauigkeit ausgeführt. Das Endergebnis wird
wie gefordert gerundet.
• Ich gebe in den Lösungen manchmal mehr Stellen an, damit Sie vergleichen können.
Aufgabe 1:
a) Ein Abwasserrohr soll entlang einer ebenen Straße auf einer Strecke s = 67,28 m mit einem
Gefälle von j = 1° verlegt werden. Am Anfang liegt das Rohr in einer Tiefe von ta = 1,24 m. In
welcher Tiefe te liegt das Ende des Rohres? (Bezeichnen Sie den Zuwachs an Tiefe mit tz).
b) Häufig werden Gefälle in der Form 1:50, 1:100, 1:150 angegeben. Berechnen Sie jeweils den
Winkel gegenüber der Ebene.
c) Eine Brücke soll einen Kanal in einer Höhe von h = 47,65 m über Straßenniveau überqueren.
Die Rampe, die zur Brücke hochführt, soll eine Steigung von 8 % haben.
r
h
j
s
Fragen:
• Über welche (ebene) Strecke s erstreckt sich die Rampe?
• Wie groß ist der Steigungswinkel der Rampe?
• Wie lang ist die Fahrbahn r der Rampe?
Aufgabe 2:
a) Auf dem First eines Daches soll ein h = 12,7 m hoher Funkmast montiert werden. Die Dachoberfläche hat gegenüber der Ebene eine Neigung von j = 28° und hat eine Ausdehnung
a = 6,82 m. Berechnen Sie den Anstand d der Mastspitze von der seitlichen Dachkante.
Hinweis: Schließen Sie aus j und dem rechten Winkel auf weitere Winkel.
d
h
a
j
b) Von den Elementen einer Konstruktion seien Seiten z = 4,97 m und r = 6,19 m und Winkel
g = 56,3° bekannt. Berechnen Sie den Winkel a:
g
z
r
a
Frage: Ist die Konstruktion mit diesen
Elementen eindeutig? Welcher
Kongruenzsatz liegt dieser
Konstruktion zugrunde?
Prof. U. Stephan
TFH Berlin, FB II
Studiengang BAU – 1. Fachsemester
LV „Mathematik“
Übung 1
Seite 2 von 5
 −2 
1
 
 
Aufgabe 3: Gegeben seien die Vektoren a = −3 und b = 5 .
 
 
 3
4
 
 
a) Berechnen Sie den Winkel zwischen den beiden Vektoren. Geben Sie den Winkel in Grad (°) und
im Bogenmaß.
b) Berechnen Sie a × b und die Länge dieses Vektors.
c) Weisen Sie nach, dass a × b senkrecht steht sowohl auf a als auch auf b .
 2 4 −2 


Aufgabe 4: Gegeben sei eine Vektorgleichung A ⋅ u = r mit A = −3 5 −19


 1 −2 7 


a) Berechnen Sie det(A), indem Sie die Determinante nach der 3. Spalte entwickeln. Zwischenschritte der Rechnung sind hinzuschreiben.
b) Welche Schlussfolgerung ziehen Sie aus dem Ergebnis hinsichtlich der Anzahl der Lösungen der
Vektorgleichung?
 2 −7 
 −4 1 
 3 2 −5 


, C =
, D = −5 3 .
Aufgabe 5: Gegeben seien die Matrizen B = 




 3 5
 −1 4 6 
6 4


Berechnen Sie alle Produkte, die definiert sind. Beachten Sie, dass es 9 mögliche Produkte gibt (nicht
nur B.C und B.D, sondern auch B.B etc.).
Prof. U. Stephan
TFH Berlin, FB II
Studiengang BAU – 1. Fachsemester
LV „Mathematik“
Übung 1
Seite 3 von 5
Lösungen:
Aufgabe 1:
a) Skizze:
s
j
tz
Erkennen:
rechtwinkliges Dreieck, Winkel j, Gegen- und Ankathete
Ansatz:
tan ϕ =
tz
s
ergibt
t z = s ⋅ tan ϕ = 1,174 m (gerundet von 1,174376…).
te = ta + tz = 2,41 m
b) Skizze und Erkennen wie bei a). Für 1:50 gilt z. B. s = 50, tz = 1.
Ansatz: tan ϕ =
ϕ1:100 = arctan
1
50
ergibt
ϕ1:50 = arctan
1
≈ 1,1° (gerundet von 1,1457…)
50
1
≈ 0,5729...°
100
c) Steigung 8% bedeutet:
h : s = 8 : 100, also
s=
•
Ebene Strecke
•
tan ϕ =
•
Pythagoras ergibt r =
8
100
ϕ1:150 = arctan
1
≈ 0,38196...°
150
h
8
=
, ergibt
s 100
100 ⋅ h
= 595,625 m
8
ergibt
ϕ = arctan 0,08 = 4,57392...°
s 2 + h 2 = 597,5279... ;
h
h
Kontrollrechnung (oder alternativ) sin ϕ =
ergibt r =
= 597,5279...
r
sin ϕ
Aufgabe 2:
a) Man berechnet zuerst Winkel b :
C
d
h
a
A
b
a
B
j
Im rechtwinkligen Dreieck folgt a = 90° - j und b = 180° - a = 180° - ( 90° - j ) = 90° + j = 118°
Überlegung: Im Dreieck ABC sind folgende Elemente am Problem beteiligt: Seiten a, h und d;
Winkel b . d ist gesucht, die anderen drei Elemente sind gegeben. Diese Konstellation ist mit dem
Prof. U. Stephan
TFH Berlin, FB II
Studiengang BAU – 1. Fachsemester
LV „Mathematik“
Übung 1
Seite 4 von 5
Cosinus-Satz lösbar, man beginnt immer mit der gesuchten Seite (bzw. der Seite, die dem Winkel
gegenüberliegt):
d 2 = a 2 + h 2 − 2ah cos β
Einsetzen der Werte ergibt d² = 289,1280198… , d = 17,004 m .
b) Man erkennt zwei Paare (Seite, gegenüberliegender Winkel). Dies deutet auf den Sinus-Satz
hin.
Bevor man den Sinus-Satz aufstellt, muss man sich die Eindeutigkeit der Konstruktion überlegen. Gegeben sind zwei Seiten und der der größeren Seite gegenüberliegende Winkel, also
eine Konstruktion nach Kongruenzsatz SsW.
Man stellt den Sinus-Satz auf, indem man mit dem unbekannten Element beginnt:
sin α sin γ
z ⋅ sin γ
=
. Multiplikation der Gleichung mit z ergibt sin α =
z
r
r
z ⋅ sin γ
und α = arcsin
= 41,91154...°
r
(Ich wiederhole meinen einführenden Hinweis: Es ist natürlich Blödsinn, auf dem Bau einen
Winkel auf 5 Stellen nach dem Komma anzugeben. Die weiteren Stellen sollen Ihnen den
Vergleich mit Ihren Berechnungen ermöglichen).
1
 −2 


 
Aufgabe 3: Gegeben seien die Vektoren a = −3 und b = 5 .
 
 
 3
4
 
 
a) Für den Winkel zwischen zwei Vektoren benutzen man die Definition des Skalarprodukts:
a ib = a ⋅ b ⋅ cos ϕ
(1)
mit ϕ =
(a , b )
Als erstes berechnet man a ib = 1 ⋅ ( −2) + ( −3) ⋅ 5 + 4 ⋅ 3 = −5 . (Anmerkung: wäre dieses Ergebnis
gleich 0, wäre man fertig, der Winkel 90° - deshalb berechnet man diesen Teil der Aufgabe zuerst).
Dann berechnet man a² = 1 + 9 + 16 = 26, also a =
Gleichung (1) aufgelöst nach cos ϕ ergibt
und
ϕ ≈ 99,15°
26 und b² = 4 + 25 + 9 = 38, also b = 38 .
cos ϕ =
a ib
−5
=
≈ −0,15907
a ⋅b
26 ⋅ 38
bzw. xϕ ≈ 1,7305 .
 −29 


b) (Siehe Formelsammlung): a × b = −11


 −1 


2
a × b = 841 + 121 + 1 = 963 , also a × b = 963 .
c) Zum Nachweis des rechten Winkels zwischen zwei Vektoren (die beide nicht der Nullvektor sind)
benutzt man das Skalarprodukt:
Prof. U. Stephan
TFH Berlin, FB II
Studiengang BAU – 1. Fachsemester
LV „Mathematik“
Übung 1
Seite 5 von 5
 −29   1 
( a × b )ia =  −11 i −3  = −29 + 33 − 4 = 0 (also: senkrecht)
 −1   4 

 
 −29   −2 
( a × b )ib =  −11 i 5  = 58 − 55 − 3 = 0 (also: senkrecht)
 −1   3 

 
Aufgabe 4:
2
a)
4
−2
−3 5
2 4
2 4
det( A) = −3 5 −19 = −2 ⋅
+ 19 ⋅
+ 7⋅
= −2 − 152 + 154 = 0
1 −2
1 −2
−3 5
1 −2 7
b) Da die Determinante der Systemmatrix A gleich Null ist, gibt es keine eindeutige Lösung, d.h. die
Anzahl der Lösungen ist nicht 1. Also gibt es entweder keine Lösung oder unendlich viele Lösungen.
Aufgabe 5:
a) Produkte der Form B.X :
 19 1 
B² = B ⋅ B = 

 3 28 
 −13 −4 26 
B ⋅C = 

 4 26 15 
B.D ist nicht definiert
C.C ist nicht definiert
 −34 −35 
C⋅D = 
43 
 14
b) Produkte der Form C.X :
C.B ist nicht definiert
c) Produkte der Form D.X :
 −29 −33 
D ⋅ B =  29 10 
 −12 26 


Bearbeitungsstand: 13.5.2008
 13 −24 −52 
D ⋅ C =  −18 2
43 
 14
28 −6 

D.D ist nicht definiert