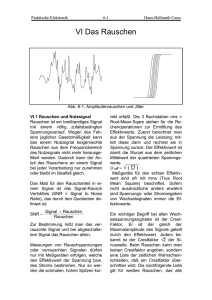
Rauschen

Physikalisches Fortgeschrittenenpraktikum
Versuchsprotokoll
Rauschen
Andreas Liehl
Maximilian Russ
Universität Konstanz
Betreuer: Markus Herz
Konstanz, den 26.02.2014
Abstract
This experiment deals with the fundamental properties of noise which is often
visible in electronic measurements and disturbs the measured signal. Particularly, we’ll investigate the properties of the so-called Johnson noise which results
from the thermal motion of the charge carriers. The Johnson noise depends
on the electical resistance where the charge carriers pass, the bandwidth with
which the measurement is taken and of course on temperature. The quantitative measurement of the Johnson noise allows to calculate the value of the
Boltzmann constant kB .
In a second part of the experiment, we’ll have a look at the so-called shot noise.
The shot noise appears if charge carriers have to get over a potential barrier.
The amount of charge carriers which pass the potential barrier is not constant
in time but fluctuates. Therefore, the measured signal begins to fluctuate. In
this case, a quantitative measurement of the shot noise allows a calculation of
the elementary charge e.
ii
Inhaltsverzeichnis
1 Einleitung und Motivation
1
2 Theoretische und experimentelle Grundlagen
2.1 Rauschen . . . . . . . . . . . . . . . . . . . . . .
2.1.1 Johnson-Rauschen . . . . . . . . . . . .
2.1.2 Schrot-Rauschen . . . . . . . . . . . . . .
2.1.3 Weißes und rosa Rauschen . . . . . . . . .
2.2 Messinstrumente und deren Funktion . . . . . . .
2.2.1 Frequenzfilter . . . . . . . . . . . . . . . .
2.2.2 Operationsverstärker . . . . . . . . . . . .
2.2.3 Elektrisches Messprinzip des Experiments
2
2
2
4
5
5
5
8
8
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Experimenteller Aufbau und Versuchsdurchführung
11
4 Ergebnisse und Diskussion
4.1 Johnson-Rauschen in Bezug auf Widerstand R und Bandbreite ∆f und
Bestimmung der Boltzmann-Konstante kB . . . . . . . . . . . . . . . . . .
4.2 Schrot-Rauschen und Bestimmung der Elementarladung e . . . . . . . . . .
4.3 Bestimmung des absoluten Temperaturnullpunkts anhand des JohnsonRauschens . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4 Fazit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
Literatur
20
Abbildungsverzeichnis
20
13
16
17
19
iii
1
1 Einleitung und Motivation
Rauschen ist in der Experimentalphysik bei elektrischen Messsignalen meist ein unliebsamer Begleiter. Oftmals sind Messungen aufgrund des Rauschens, der Überlagerung des
eigentlichen Messsignals mit zufälligen Fluktuationen im Signal, gar nicht möglich, da dessen Stärke das eigentliche Messsignal überragt.
Im Alltag begegnet man Rauschen häufig im Ultrakurzwellenrundfunk, das Rauschen führt
hier oftmals zu einer Verzerrung des akustischen Signals bei Radioübertragungen [1].
Es gibt unterschiedliche Arten von Rauschen, beispielsweise können externe Störquellen,
wie z.B. zufällige elektromagnetische Felder oder fehlerhafte elektrische Kontakte, was zu
einem variablen elektrischen Widerstand am Kontakt führt, ein elektrisches Messsignal beeinflussen. Durch ausreichende Abschirmung der Messapparatur sowie präzisem Vorgehen
lassen sich diese Rauschquellen minimieren. In diesem Experiment hingegen sollen zwei unvermeidbare Rauschquellen untersucht werden. Zunächst wird das thermische Rauschen,
das sog. Johnson-Rauschen, welches durch die thermische Bewegung der Ladungsträger,
in etwa vergleichbar mit der Brownschen Molekularbewegung auftritt, beobachtet. Weiter
tritt das sog. Schrot-Rauschen (engl. shot noise) durch die statistische Fluktuation der Anzahl der Ladungsträger, die eine Stelle im Leiter passieren und damit zu einem Stromfluss
beitragen, in elektronischen Messungen auf und wird im Experiment ebenfalls untersucht.
[2].
Neben der Untersuchung der Temperaturabhängigkeit des Rauschens lassen sich aus den
Messungen die Naturkonstanten kB und e bestimmen.
2 Theoretische und experimentelle Grundlagen
2
2 Theoretische und experimentelle Grundlagen
In diesem Abschnitt sollen zunächst die theoretischen Grundlagen des Rauschens sowie die
im Experiment verwendete Messvorrichtung erläutert werden.
2.1 Rauschen
Wie bereits in Abschnitt 1 erwähnt, gibt es mehrere Quellen, die zu einem verrauschten
Messsignal führen können. Eine davon ist die Kopplung der Messvorrichtung mit dessen
Umgebung, was auch als Interferenz bezeichnet wird. Im Wesentlichen können hier drei
Hauptquellen, die zum Rauschen führen, unterschieden werden: die elektrostatische Kopplung, Kopplung an externe elektromagnetische Felder, sowie mechanische Vibrationen an
der Versuchsapparatur, sofern diese an das Signal ankoppeln [2].
Eine weitere Quelle für Rauschen, die im übrigen durch präzise Arbeitsweise durchaus minimiert werden kann, bezeichnet man als technisches Rauschen und umfasst alle Defekte
an der Messvorrichtung, wie beispielsweise schwache elektrische Kontakte [2].
Der Fokus in diesem Experiment soll jedoch auf zwei unvermeidlichen Rauschquellen liegen: zum einen das Johnson-Rauschen (oftmals auch als Johnson-Nyquist-Rauschen
bezeichnet) und zum anderen das Schrot-Rauschen. Wie bereits in Abschnitt 1 erwähnt,
sind beide Rauschtypen physikalischer Natur und bilden daher bei gegebener Apparatur
eine Grenze des Auflösungsvermögens von elektrischen Messsignalen. Im Folgenden sollen
typische Eigenschaften der beiden Rauschtypen näher erläutert werden.
2.1.1 Johnson-Rauschen
Wie bereits in Abschnitt 1 erwähnt, liegt der Ursprung des Johnson-Rauschens in der
Brownschen Molekularbewegung, der zufälligen Bewegung von Atomen oder Molekülen
in Flüssigkeiten und Gasen aufgrund deren thermischer Energie, der Ladungsträger. Da
die Brownsche Molekularbewegung thermischer Natur ist, bezeichnet man das JohnsonRauschen auch als thermisches Rauschen. Die Brownsche Molekularbewegung wird bei
abnehmender Temperatur geringer, von daher ist es nicht verwunderlich, dass auch das
Johnson-Rauschen bei geringen Temperaturen weniger ins Gewicht fällt.
Für eine quantitative Beschreibung des Johnson-Rauschens betrachten wir das durch das
Rauschen verursachte zusätzliche Messsignal. Fließt durch einen elektrischen Widerstand
R ein elektrischer Strom I, so fällt an diesem gemäß dem Ohmschen Gesetz die Spannung
U = RI ab. Für I = 0 sollte also auch keine Spannung abfallen. Dies ist aufgrund des oben
angesprochenen Johnson-Rauschens in der Praxis jedoch nicht der Fall und es ist eine
zeitlich fluktuierende Spannung messbar. Diese Spannung sei im Folgenden mit UJ = UJ (t)
bezeichnet. Da das Rauschen - ebenso wie die Brownsche Molekularbewegung - zufällig
ist, verschwindet die zusätzliche Spannungsamplitude im zeitlichen Mittel:
hUJ (t)i = 0.
(2.1)
Um das Rauschen zu charakterisieren, verwendet man von daher Messtechniken, die das
Messsignal quadrieren. Die Amplitude des quadrierten Signals verschwindet im zeitlichen
Mittel nicht mehr. Der Zusammenhang zwischen mittlerer quadratischer Abweichung der
3
2.1 Rauschen
am Widerstand abfallenden Spannung konnte 1928 von Nyquist aufgestellt [3] und von
Johnson experimentell bestätigt werden [4]. Es gilt:
D
UJ (t)2
E
Z t2
1
UJ (t)2 dt
t2 − t1 t1
= 4kB T R∆f,
=
(2.2)
wobei T die Temperatur, R der elektrische Widerstand und ∆f die Bandbreite der Messung ist. Diese Formel wird auch als Nyquist-Formel bezeichnet. Die Abhängigkeit der
Spannungsamplitude UJ (t) von der Bandbreite der Messung ist offensichtlich, da das Rauschen als eine Überlagerung unendlich vieler Frequenzen zu verstehen ist. Da jede Frequenz
einen Energiebeitrag zum Rauschen leistet, kann die Spannungsamplitude UJ (t) nicht unabhängig von der Bandbreite sein [2]. Um die Bandbreite zu definieren verwenden wir in
diesem Experiment einen Bandpass-Filter, auf dessen Funktionsweise in Abschnitt 2.2.1
noch eingegangen wird.
Gleichung (2.2) soll im Experiment verwendet werden um sowohl die Boltzmann-Konstante
kB , als auch den absoluten Nullpunkt der Temperatur zu bestimmen. Oftmals definiert
man hier die sog. Rauschdichte S, manchmal auch als spektrale Rauschleistungsdichte
(engl. PSD = Power Spectral Density) bezeichnet, als mittlere quadratische Abweichung
der Spannungsamplitude pro Frequenzintervall1 [2]:
D
E
UJ (t)2
S=
= 4kB RT .
(2.3)
∆f
D
E
Misst man nun UJ (t)2 bei bekannter Temperatur T , bekanntem Widerstand R und
wohldefinierter Bandbreite, so lässt sich die Boltzmann-Konstante bestimmen. Ebenso
lässt sich der absolute Temperaturnullpunkt bestimmen, indem mehrere Messwerte bei
verschiedenen Temperaturen aufgenommen werden. Der gemäß Gleichung (2.3) lineare Zusammenhang sollte idealerweise eine Ursprungsgerade, d.h. T0 = 0 K liefern.
Es soll nun noch die Größenordnung des Johnson-Rauschens abgeschätzt werden. Wir
betrachten hierzu einen 100 − kΩ-Widerstand bei Raumtemperatur und eine Messung mit
einer Bandbreite von ∆f = 100 kHz, was durch einen Bandpass, der Frequenzen oberhalb
von 100 kHz herausfiltert2 , Drealisiert
E werden kann. Für die mittlere quadratische Span2
nungsamplitude ergibt sich UJ (t) ≈ 10−10 V2 . Da jedoch die Einheit V2 relativ unanschaulich ist, gibt man häufig die Wurzel aus der mittleren quadratischen Abweichung an,
was auch als quadratisches Mittel (engl. root mean square bzw. rms) bezeichnet wird. Man
erhält für obiges Beispiel ein Messsignal mit zeitlich fluktuierender Spannung im Bereich
von [2]
rD
E
∆U = UJ,rms =
1
UJ (t)2 ≈ 10 µV.
(2.4)
Tatsächlich ist die Rauschdichte in dieser Definition noch keine spektrale Leistungsdichte, was man sich
2
an dessen Einheit verdeutlichen kann: [S] = V
. Wird die Rauschdichte hingegen auf den Widerstand
Hz
bezogen, also als Rauschdichte pro Widerstand, ergibt sich auch von der Einheit eine spektrale LeisS
W
tungsdichte: R
= Hz
. In diesem Fall spricht man auch von der spektralen Rauschleistungsdichte des
Widerstands.
2
Bandpässe, die Frequenzen oberhalb einer bestimmten Frequenz herausfiltern werden auch als Tiefpässe
bezeichnet.
2 Theoretische und experimentelle Grundlagen
4
Durch das Johnson-Rauschen lässt sich ebenso das thermische Gleichgewicht zweier Leiter erklären, die energetisch nur durch eine koaxiale Leitung und nicht thermisch gekoppelt
sind. Es sei angenommen, dass beide Widerstände identisch sind (R1 = R2 = R) und die
koaxiale Leitung ebenso die Impedanz Z = R aufweist, damit keine Verluste durch Reflexion auftreten. Jedoch seien die Widerstände zu Beginn auf unterschiedlicher Temperatur.
Durch das Johnson-Rauschen fungieren beide Widerstände als schwarze Körper und deren Strahlung kann durch die koaxiale Leitung ausgetauscht werden. Dadurch stellt sich
schließlich ein thermisches Gleichgewicht zwischen den Widerständen ein [2]. Durch dieses
Gedankenexperiment konnte Nyquist letztendlich seine theoretischen Beschreibungen des
Johnson-Rauschens aufstellen [1, 3].
2.1.2 Schrot-Rauschen
Das Schrot-Rauschen kommt, wie ebenfalls bereits in Abschnitt 1 erwähnt, durch die Ladungsquantisierung zustande. In der Praxis ist gemessener elektrischer Strom I nichts
anderes als die Detektion der Anzahl n der Elektronen in einer gewissen Zeitspanne τ , die
alle die Ladung −e tragen3 . Es gilt hier [2]:
n=
Q
Iτ
=
.
e
e
(2.5)
Die Anzahl der Elektronen, die eine Potentialbarriere passieren, ist allerdings nicht konstant sondern statistisch verteilt. Unter Annahme unabhängiger Ladungsträger folgt die
Anzahl der detektierten Elektronen der Poisson-Statistik, d.h. es wird im Zeitintervall τ
√
die fluktuierende Anzahl n ± n an Elektronen gemessen [1]. Die Ladung fluktuiert also
mit Standardabweichung
√
√
σQ = e n = Iτ e
und damit ergibt sich eine Fluktuation der gemessenen Stromstärke von
r
σQ
Ie
σI =
=
.
τ
τ
(2.6)
Gemessen wird im Experiment die mittlere quadratische Abweichung der elektrischen
Stromstärke:
D
E
Ie
∆I (t)2 = σI2 = .
(2.7)
τ
Da jedoch auch hier die Definition eines Zeitintervalls τ der Messung schwierig ist, definiert
man die Fluktuation der Stromstärke, wie bereits beim Johnson-Rauschen die Definition
der Fluktuation der Spannung in Abschnitt 2.1.1, anhand der Bandbreite. Schottky
konnte dabei folgenden Zusammenhang ableiten [2]:
D
E
∆I (t)2 = 2Ie∆f .
(2.8)
Das Schrot-Rauschen ist also im Wesentlichen proportional zur gemessenen Stromstärke, was nicht verwunderlich ist, da gemäß der Poisson-Statistik ein größeres Messsignal
3
Zur Vereinfachung wird im Folgenden das Vorzeichen der Ladung nicht immer berücksichtigt.
5
2.2 Messinstrumente und deren Funktion
auch zu einer stärkeren Fluktuation führt. Die Abhängigkeit des Schrot-Rauschens von der
Bandbreite ergibt sich analog zur Überlegung zur Abhängigkeit des Johnson-Rauschens
von Letzterer in Abschnitt 2.1.1.
Auch hier soll die Größenordnung des Schrot-Rauschens anhand eines kurzen Zahlenbeispiels abgeschätzt werden. Betrachten wir wie in Abschnitt 2.1.1 die Bandbreite ∆f =
100 kHz und eine Stromstärke von I = 10 µA, was mit modernen hochauflösenden Ampèremetern durchaus mühelos detektierbar ist, so ergibt sich ein quadratisches Mittel der Fluktuationen der Stromstärke von
rD
E
∆I =
∆I (t)2 ≈ 0,57 nA.
(2.9)
2.1.3 Weißes und rosa Rauschen
Im Allgemeinen unterscheidet man zwischen weißem und rosa Rauschen. Die Klassifikation
erfolgt dabei anhand deren Rauschdichte. Während beim weißen Rauschen die Rauschdichte nicht frequenzabhängig ist, gilt für rosa Rauschen S ∝ f1 und wird von daher auch als
1/f -Rauschen bezeichnet. Gemäß dieser Definition sind also sowohl Johnson- als auch
Schrot-Rauschen weißes Rauschen. Für genügend niedrige Frequenzen dominiert das rosa Rauschen und für hohe Frequenzen das weiße Rauschen. Dieser Zusammenhang ist in
Abbildung (2.1) dargestellt [5].
Abbildung 2.1: Die Abbildung zeigt die Abhängigkeit der Rauschdichte von der Frequenz
bei weißem und rosa Rauschen [5].
2.2 Messinstrumente und deren Funktion
Für das Experiment werden einige elektronische Bauteile verwendet, auf deren Funktion
und Anwendung im Experiment in diesem Abschnitt eingegangen wird.
2.2.1 Frequenzfilter
Ein Frequenzfilter ist ein elektronisches Bauteil, welches aus einem Eingangssignal bestehend aus einer Überlagerung sehr vieler Frequenzen einen bestimmten Frequenzbereich
2 Theoretische und experimentelle Grundlagen
6
herausfiltert. Das Ausgangssignal enthält nur noch die Anteile der durchgelassenen Frequenzen. Man unterscheidet zwischen Hoch-, Tief- und Bandpässen, die im Folgenden kurz
erläutert werden.
Hochpass Ein Hochpass ist ein Frequenzfilter, der tiefe Frequenzen aus dem Eingangssignal herausfiltert und hohe Frequenzen passieren lässt. Man unterscheidet zwischen RCund LC-Hochpässen. Abbildung (2.2a) zeigt das Schaltbild eines RC-Hochpasses erster
Ordnung. Gemäß der Kirchhoffschen Maschenregel lässt sich das Verhältnis zwischen
Eingangs- und Ausgangsspannung berechnen:
Ua R
1
=
,
(2.10)
Ue |R + XC | = q
1
1 + (ωRC)
2
wobei Ua die Amplitude der Ausgangsspannung, Ue die Amplitude der Eingangsspannung
1
und XC = −i ωC
der kapazitive Widerstand bei einer Wechselspannung mit Frequenz ω als
Eingangssignal ist. Dieses Verhältnis ist in Abbildung (2.2b) dargestellt.
Tiefpass Ein Tiefpass hingegen filtert hohe Frequenzen heraus und lässt nur tiefe passieren. Auch hier lassen sich RC- und LC-Tiefpässe konstruieren. Die Schaltskizze eines
LC-Tiefpasses zeigt Abbildung (2.2c). Analog zum RC-Hochpass gilt für das Verhältnis
zwischen Eingangs- und Ausgangsspannung:
Ua 1
= |XC | = q
.
(2.11)
Ue |R + XC |
1 + (ωRC)2
Dieses Verhältnis zeigt Abbildung (2.2d). LC-Hoch- und Tiefpässe lassen sich analog konstruieren.
Bandpass Ein Bandpass ist ein elektronisches Bauteil, welches nur Frequenzen eines
bestimmten Frequenzintervalls durchlässt, alle anderen Frequenzen werden herausgefiltert.
Eine mögliche Anordnung für einen Bandpass ist in Abbildung (2.2e) gezeigt. Dabei gilt
wieder für das Verhältnis zwischen Eingangs- und Ausgangssignal [6]
Ua 1
= q
(2.12)
Ue 2 ,
L
1
1 + ωR
− ωRC
d.h. es ergibt sich ein Maximum der Ausgangsspannung bei der Resonanzfrequenz ω =
√ 1 . Dies ist in Abbildung (2.2f) dargestellt. Die Bandbreite ∆f ist über die Breite des
LC
um die Resonanzfrequenz zentrierten Peaks definiert.
Im Experiment realisieren wir den Bandpass durch eine Reihenschaltung von Hoch- und
Tiefpass.
Ebenso lassen sich auch Band-Stop-Filter konstruieren, die alle Frequenzen außer eines
definierten Frequenzintervalls ∆f passieren lassen.
Die Tatsache, dass der kapazitive bzw. induktive Widerstand komplex ist, äußert sich
bei allen analogen Frequenzfiltern in einer Phasenverschiebung zwischen Eingangs- und
Ausgangssignal.
7
2.2 Messinstrumente und deren Funktion
1
- - Ua - Ue -
0 −2
10
0
2
10
10
ωRC
(a) Schaltplan eines RC-Hochpass
(b) Durchlasskurve eines RC-Hochpass
1
- - Ua - Ue -
0 −2
10
0
2
10
10
ωRC
(c) Schaltplan eines RC-Tiefpass
(d) Durchlasskurve eines RC-Tiefpass
1
- - Ua - Ue -
0 −2
10
(e) Schaltplan eines Bandpass
0
10
√
ω LC
2
10
(f) Durchlasskurve eines RLC-Bandpass
Abbildung 2.2: Die Abbildung zeigt die Schaltpläne von (a) RC-Hochpass, (c) RC-Tiefpass
und (e) einer möglichen Konfiguration eines Bandpass [6]. Ebenso sind die
Verhältnisse von Ausgangs- und Eingangsspannung in Abhängigkeit der
Frequenz gezeigt (b),(d),(f). Man beachte die logarithmische Skala.
8
2 Theoretische und experimentelle Grundlagen
2.2.2 Operationsverstärker
In den Abschnitten 2.1.1 und 2.1.2 wurde die Größenordnung des Rauschens abgeschätzt.
Da die Amplitude des Johnson-Rauschens sehr gering ist (siehe auch Gleichung (2.4)),
muss das Rauschsignal verstärkt werden, um es auf dem Oszilloskop sichtbar zu machen.
Dazu wird ein sog. Operationsverstärker verwendet. Ein Operationsverstärker ist ein elektronisches Bauteil, welches zwei Eingänge besitzt, die mit “+“ und “−“ bezeichnet werden
[2]. Die zum Betrieb des im Experiment verwendeten Verstärkers, ein sog. nicht invertierender Verstärker, wobei die Bezeichnung daher rührt, dass Eingangs- und Ausgangssignal
dasselbe Vorzeichen besitzen, notwendige elektrische Schaltung ist in Abbildung (2.3) dargestellt. Ebenso gibt es auch invertierende Operationsverstärker, auf die hier jedoch nicht
eingegangen werden soll.
Das Eingangssignal Ue geht hier über den “+“-Eingang in den Verstärker, am “−“-Eingang
ist ein Widerstand angeschlossen. Durch die resistive Rückkopplung des Ausgangssignals
Ua an den “−“-Eingang des Verstärkers kann die Potentialdifferenz der beiden Eingänge am
Verstärker kontrolliert werden. Man spricht hier auch von Gegenkopplung, wird das Eingangssignal über den “−“-Eingang in den Verstärker geleitet und die Rückkopplung über
den “+“-Eingang realisiert, spricht man von Mitkopplung. Dabei wird die Rückkopplung
stets so kontrolliert, dass die Potentialdifferenz zwischen den Eingängen des Verstärkers
verschwindet. Damit lässt sich die Ausgangsspannung gemäß der Maschenregel berechnen
und es gilt [7, Abb. (2.3)]:
R2
Ua = Ue · 1 +
.
(2.13)
R1
Ue
R2
Ua
R1
Abbildung 2.3: Die Abbildung zeigt den Schaltplan des verwendeten Operationsverstärkers
[7].
2.2.3 Elektrisches Messprinzip des Experiments
In diesem Abschnitt soll kurz die elektrische Schaltung des Experiments erläutert werden.
Der Schaltplan des Experiments zur Messung des Johnson-Rauschens ist in Abbildung
(2.4) dargestellt.
Die an einem Widerstand Rin abfallende Spannung des Johnson-Rauschens UJ (t) wird
zunächst in einem Vorverstärker (engl. preamplifier) um einen Faktor Gpre verstärkt4 . An4
Die Bezeichnung G für die Verstärkung rührt aus dem Englischen - engl. gain = Verstärkung.
9
2.2 Messinstrumente und deren Funktion
Abbildung 2.4: Die Abbildung zeigt den Schaltplan zur Messung des Johnson-Rauschens.
Um das Schrot-Rauschen zu messen muss der Aufbau leicht modifiziert
werden [2].
schließend wird die Bandbreite des Signals definiert, indem zunächst in einem Hochpassund anschließend in einem Tiefpassfilter niedrige und hohe Frequenzen gefiltert werden.
Im Experiment verwenden wir Bandbreiten im Bereich von ∆f = 0,1 − 100 kHz. Anschließend wird das Signal nochmals im Hauptverstärker durch den Faktor Gmain verstärkt.
Das nun ausreichend verstärkte Messsignal wird auf einem Oszilloskop ausgelesen. Um
jedoch die mittlere quadratische Abweichung der Spannungsamplitude zu erhalten, was
gemäß Gleichung (2.2) für weitere Berechnungen notwendig ist, muss die Spannung des
Johnson-Rauschens quadriert werden, was mithilfe eines Quadrierers (engl. multiplier)
bewerkstelligt wird. Dieser liefert im Ausgang das zeitliche Mittel des Spannungsquadrats
um den Faktor 101V reduziert, was schließlich am Multimeter (DMM = digital multimeter)
ausgelesen word. Die Einheit, des ausgelesenen Signals UDMM ist also V. Es gilt [2]:
UDMM =
E
G2pre G2main D
· UJ (t)2 .
10 V
(2.14)
Zur Messung des Schrot-Rauschens wird die Schaltung leicht modifiziert. Zunächst ist
ein elektronisches Bauteil notwendig, an welchem das Schrot-Rauschen vermessen werden
kann, hier wird eine Photodiode verwendet. Der gemessene Photostrom Iph wird direkt
über ein weiteres Multimeter detektiert. Das Rauschsignal wird wieder durch die Anordnung aus Abbildung (2.4) detektiert und das zeitliche Mittel der Spannungsschwankung
aus Gleichung (2.14) kann direkt über das Ohmsche Gesetz in eine Stromstärke umgerechnet werden [2].
Bisher wurde generell das Rauschen an einem Widerstand Rin betrachtet und dabei die
Messapparatur als ideal angenommen, d.h. das Rauschen der Apparatur, insbesondere das
Rauschen der Verstärker, vernachlässigt. In der Praxis kann diese Annahme jedoch nicht
getroffen werden, viel mehr verursacht die Messanordnung eine zusätzliche Rauschspannung Uext (t). Für das resultierende Ausgangssignal Uges (t) gilt also:
Uges (t) = UJ (t) + Uext (t).
2 Theoretische und experimentelle Grundlagen
10
Dieses durch die Verstärker verursachte Rauschen lässt sich jedoch ebenfalls messen und
damit vom gesamten Messsignal subtrahieren. Dazu wird die Annahme getroffen, dass Uext
jene Spannung bezeichnet, welche zwar durch den Verstärker verursacht wird, jedoch bereits
vor dem Verstärker auftritt und anschließend von einem idealen, rauschlosen Verstärker mit
gleicher Verstärkung G verstärkt wird. Weiter sein angenommen, dass das unkorrelierte
Rauschen des Verstärkers nicht von dessen Eingangsspannung abhängt. Für das verstärkte
Signal gilt damit
Uges,amp (t) = G · (UJ (t) + Uext (t))
und für das quadratische zeitliche Mittel gilt folgender Zusammenhang:
D
Uges,amp (t)2
E
E
(UJ (t) + Uext (t))2
D
E
D
E
=
UJ (t)2 + 2 · hUJ (t) · Uext (t)i + Uext (t)2 .
∝
D
Die beiden Signale können als unkorreliert und mittelwertfrei angenommen werden, was
dadurch zu rechtfertigen ist, dass sie unterschiedlichen Objekten entstammen. Dadurch
verschwindet unter Verwendung von Gleichung (2.1) der Mischterm gemäß:
(2 1)
hUJ (t) · Uext (t)i = hUJ (t)i · hUext (t)i = 0.
Damit ist
D
E D
E D
E
Uges,amp (t)2 ∝ UJ (t)2 + Uext (t)2 ,
(2.15)
D
E
wodurch eine Messung von Uext (t)2 möglich wird, indem der Widerstand Rin , an dem
das Johnson-Rauschen vermessen wird, hinreichend klein gewählt wird, sodass das Johnson-Rauschen an diesem Widerstand im Vergleich zum Rauschen des Verstärkers vernachlässigt werden kann. Typische Größenordnungen des externen Rauschens liegen im Experiment bei Uext,rms ≈ 1 µV [2].
11
3 Experimenteller Aufbau und Versuchsdurchführung
In diesem Abschnitt soll kurz der Versuchsaufbau und das experimentelle Vorgehen geschildert werden.
Wie bereits in Abschnitt 2.2.3 erläutert, ist der experimentelle Aufbau zur Vermessung
des Johnson-Rauschens in Abbildung (2.4) dargestellt. Es wird lediglich eine kleine Änderung vorgenommen, dergestalt, dass der Hochpass-Filter entfernt wurde. Es lassen sich
dann über die Kontrolleinheit Bandbreiten von
∆f = 0,33 kHz , 1 kHz , 3,3 kHz , 10 kHz , 33 kHz und 100 kHz
einstellen. Hierbei ist zu beachten, dass die tatsächliche Bandbreite um einen Faktor 1,1108
größer ist. Dies rührt aus der Tatsache, dass, wie an Abbildung (2.2) zu sehen ist, ein gewisser Anteil der gefilterten Frequenzen immer noch durchgelassen wird. Es wird aus diesem
Grund eine effektive Bandbreite definiert, die sich bei den hier speziell verwendeten Filtern gemäß Herstellerangaben um oben genannten Faktor im Vergleich zum ursprünglichen
Wert verändert [2]. Zur Kontrolle der durchgelassenen Bandbreiten wird auf dem Oszilloskop zusätzlich die Fourier-Transformation des Rauschsignals beobachtet.
Ebenso lässt sich der Widerstand, an dem das Johnson-Rauschen vermessen wird, mit
Werten von
Rin = 1 Ω , 10 Ω , 100 Ω , 1 kΩ , 10 kΩ , 100 kΩ und 1 MΩ
einstellen.
Zur Messung des Johnson-Rauschens wird wie in Abschnitt 2.2.3 geschildert zunächst das
Rauschen der Verarbeitungskette des Messsignals für jede Bandbreite bestimmt. Dazu wird
am Eingangswiderstand der Wert Rin = 1 Ω eingestellt, damit das Johnson-Rauschen hier
so gering wird, dass es im Vergleich zum Rauschen der Signalverarbeitungskette vernachlässigt werden kann. Der so bestimmte Offset kann später von den Messwerten für höhere
Eingangswiderstände abgezogen werden.
Bei der quantitativen Messung des Johnson-Rauschens werden die Widerstände am Operationsvorverstärker (siehe auch Abbildung (2.3)) so kontrolliert, dass sich ein Vorverstärkungsfaktor von Gpre = 600 ergibt. Weiter wird hier sowie bei allen folgenden Messungen
am Quadrierer eine Zeitkonstante von τ = 1 s gewählt, d.h. die Berechnung des Mittelwerts
der quadrierten Rauschspannung erfolgt anhand einer zeitlichen Integration über den Zeitraum von einer Sekunde. Dies ist insofern von entscheidender Bedeutung, da eine zu kurze
Zeitkonstante hier zu fluktuierenden Werten führen würde, was auf die Ergoden-Theorie
zurückzuführen ist.
Am Hauptverstärker kann das Messsignal nochmals um einen Faktor Gmain ≤ 10000 verstärkt werden.
Um nun die Nyquist-Formel (Gleichung (2.2)) auf Proportionalität
zu Widerstand und
D
E
2
5
Bandbreite zu überprüfen, wird die Rauschspannung UJ (t) für jede Kombination aus
Bandbreite und Widerstand bestimmt. Aus diesen Werten lässt sich schließlich die Boltzmann-Konstante kB bestimmen. Dabei, wie auch bei allen anderen Messungen, wird die
5
An dieser Stelle sei darauf hingewiesen, dass im Folgenden die Bezeichnung
Rauschspannung
simultan
für den Mittelwert der quadrierten zeitlich fluktuierenden Rauschspannung UJ (t)2 und die eigentliche
Rauschspannung UJ (t) verwendet wird. Was jeweils gemeint ist, ergibt sich aus dem Zusammenhang.
Analog wird die Bezeichnung Rauschstrom beim Schrot-Rauschen verwendet.
3 Experimenteller Aufbau und Versuchsdurchführung
12
Verstärkung am Hauptverstärker in der Verarbeitungskette stets so gewählt, dass die verstärkte Spannung am digitalen Multimeter im Bereich von UDMM ≈ 1 V liegt, da für höhere
Spannungen die Gefahr besteht, dass der Messbereich des Oszilloskops nicht ausreicht und
der Detektor in die Sättigung gerät.
Wie ebenfalls in Abschnitt 2.2.3 geschildert, wird zur experimentellen Beobachtung des
Schrot-Rauschens eine Photodiode in das Gehäuse der Kontrolleinheit eingebaut, die mit
einer Glühbirne bestrahlt wird. Da sich Glühbirne und Photodiode innerhalb des Gehäuses befinden, ist eine zusätzliche externe Beleuchtung der Photodiode weitestgehend vermieden. Die Intensität der Glühbirne und damit der Photostrom IPh lässt sich über die
Kontrolleinheit steuern. Die Photodiode ist dabei parallel zum fest eingestellten
EingangsD
E
widerstand Rin = 10 kΩ geschaltet, über welchem die Rauschspannung ∆U (t)2 abgegriffen wird, aus welcher sich schließlich der Rauschstrom ergibt. Die Vorverstärkung des
Operationsverstärkers beträgt nun Gpre = 100. Auch hier wird für IPh = 0 A zunächst der
Offset der Rauschspannung, der aus dem Rauschen der Signalverarbeitungskette rührt,
bestimmt. Anschließend wird zur Verifikation von Gleichung (2.8) und zur Bestimmung
der Elementarladung e für die Bandbreiten ∆f = 3,3 kHz , 10 kHz , 33 kHz und 100 kHz
und verschiedene Photoströme im Bereich von IPh
D = 0 − 100
E µA die Rauschspannung be2
stimmt, woraus sich schließlich der Rauschstrom ∆I (t) gemäß dem Ohmschen Gesetz
ergibt.
Im letzten Versuchsteil wird die Temperaturabhängigkeit des Johnson-Rauschens untersucht. Dazu werden externe Widerstände mit Werten von Rin = 10 Ω , 10 kΩ und 100 kΩ
vermessen. Der kleinste Widerstand dient dabei wieder zur Bestimmung des Offsets. Die
Rauschspannung der externen Widerstände wird wieder für verschiedene Bandbreiten von
∆f = 1 kHz , 3,3 kHz und 10 kHz jeweils bei Raumtemperatur und bei T = 77 K, der
Siedetemperatur von flüssigem Stickstoff, in welchen die Widerstände abgesenkt werden,
bestimmt. Durch den resultierenden linearen Zusammenhang sollte sich später idealerweise
der absolute Temperaturnullpunkt T0 = 0 K ergeben.
13
4 Ergebnisse und Diskussion
In diesem Abschnitt werden die experimentellen Ergebnisse präsentiert und deren physikalischer Inhalt diskutiert.
4.1 Johnson-Rauschen in Bezug auf Widerstand R und Bandbreite ∆f
und Bestimmung der Boltzmann-Konstante kB
Zunächst wird die Nyquist-Formel in Bezug auf DBandbreite
E ∆f und Widerstand Rin un2
tersucht. Dazu wird jeweils die Rauschspannung UJ (t) über der jeweiligen Größe aufgetragen, was in einem linearen Zusammenhang resultieren sollte. Dies ist in Abbildungen
(4.1) und (4.2) und gezeigt, in beiden Diagrammen wurde der Offset aus der Signalverarbeitungskette bereits herausgerechnet. Hierbei wurde - wie in allen weiteren Plots - auf
die Fehlerbalken verzichtet, da sie im Diagramm ohnehin verschwindend klein wären. Dies
liegt vor allem daran, dass die Rauschspannung sehr genau abgelesen werden konnte und
nur wenig fluktuierte. Die Unsicherheit der daraus resultierenden Größen ergibt sich im
Wesentlichen aus statistischer Streuung der Messwerte. Man beachte hier, dass in beiden
−10
−12
10
−14
10
R = 0,1 kΩ
R = 1 kΩ
R = 10 kΩ
R = 100 kΩ
R = 1000 kΩ
D
UJ (t)
2
E
/
V2
10
−16
10
−1
10
0
1
10
∆f
10
/
2
10
kHz
Abbildung 4.1: D
Die Abbildung
zeigt die gemessene Abhängigkeit der Rauschspannung
E
2
UJ (t) des Johnson-Rauschens von der Bandbreite ∆f in doppelt logarithmischer Skala. Der Zusammenhang ist wie erwartet linear.
14
4 Ergebnisse und Diskussion
−10
−12
10
−14
∆ f = 0,33 kHz
∆ f = 1 kHz
∆ f = 3,3 kHz
∆ f = 10 kHz
∆ f = 33 kHz
∆ f = 100 kHz
10
D
UJ (t)
2
E
/
V2
10
−16
10
0
2
10
Rin
10
/
kΩ
Abbildung 4.2: D
Die Abbildung
zeigt die gemessene Abhängigkeit der Rauschspannung
E
2
UJ (t) des Johnson-Rauschens vom Widerstand Rin in doppelt logarithmischer Skala. Der Zusammenhang ist wie erwartet linear.
Graphen eine doppelt logarithmische Skala gewählt wurde, was aufgrund der Rechengesetze des Logarithmus und gemäß Gleichung (2.2) dazu führt, dass alle Geraden eine gleiche
Steigung jedoch einen horizontalen Versatz relativ zueinander aufweisen.
Die linearen Fits, welche in allen Fällen - bis auf wenige Ausnahmen, die sich jedoch auch
sehr leicht erklären lassen (siehe unten) - sehr gut auf die Messdaten passen, bestätigen die
Nyquist-Formel. In beiden Fällen wurde für die linearen Fits jeweils eine lineare Funktion
angesetzt. Streng genommen müsste jedoch um einen zusätzlichen Offset unbekannter Herkunft ausschließen zu können eine affin lineare Funktion als Modell herangezogen werden.
Dies würde jedoch in der doppelt logarithmischen Skala zu einem nichtlinearen Zusammenhang führen. Aus diesem Grund wurde zunächst bei jeder Messreihe ein affin lineares
Modell als Fit gewählt und anschließend der Offset im Rahmen der Ungenauigkeit als verschwindend verifiziert. Die linearen Fits in Abbildungen (4.1) und (4.2) basieren alle auf
den streng linearen Fitfunktionen.
Es zeigen sich bei den Messreihen einige wenige Ausnahmen. Wie vor allem bei den Messwerten mit dem höchsten Widerstand Rin = 1000 kΩ zu sehen ist, weichen die Messwerte
für hohe Bandbreiten von dem zu erwartenden linearen Zusammenhang ab (siehe Abbildung (4.1)). Dies lässt sich dadurch erklären, dass die verwendeten Kabel in der Signalverarbeitungskette ebenfalls eine Kapazität C aufweisen. In Kombination mit dem Eingangswiderstand Rin bildet sich hier ein zusätzlicher RC-Tiefpass, welcher gemäß Gleichung (2.11)
vor allem bei hohen Eingangswiderständen zusätzlich hohe Frequenzen herausfiltert, was
4.1 Johnson-Rauschen in Bezug auf Widerstand R und Bandbreite ∆f und
15
Bestimmung der Boltzmann-Konstante kB
D
E
die effektive Bandbreite und somit die Rauschspannung UJ (t)2 zusätzlich verringert.
Eine weitere Auffälligkeit ist, dass die Messwerte für den geringsten Widerstand Rin =
100 Ω und die beiden geringsten Bandbreiten in den Diagrammen
aufgeführt sind.
D nicht E
2
Hier war im Rahmen des Messunsicherheit die Rauschspannung UJ (t) am Eingangswiderstand nicht messbar größer als die der Signalverarbeitungskette und konnte deshalb
nicht ausreichend genau bestimmt werden. Tatsächlich wurde bei der Bestimmung der
Rauschspannung der Signalverarbeitungskette auch ein minimal zu großer Wert bestimmt,
da immer noch ein - wenn auch verschwindend kleiner - Eingangswiderstand vorhanden
war. Dies führt letztendlich zu kleinen systematischen Fehler, der vor allem bei kleinen
Eingangswiderständen und Bandbreiten ins Gewicht fällt.
Zur Berechnung der Boltzmann-Konstante werden aus diesem Grund diese, sowie die
Messwerte, die aus oben genannten Gründen eine Abweichung des linearen Zusammenhangs liefern, nicht berücksichtigt.
Für alle anderen Messwerte, bei denen kein unvermeidbarer systematischer Fehler auftritt,
wird zur Berechnung der Boltzmann-Konstante die Nyquist-Formel (Gleichung (2.2))
nach der Boltzmann-Konstante umgeformt und so erhalten wir für alle Messwerte einen
Wert für kB , welche wir anschließend mitteln. Die Messwerte sind im Wesentlichen statistisch verteilt und als Fehler wird von daher die Standardabweichung angenommen. Für die
Temperatur wird eine Raumtemperatur von T = (293 ± 2) K angenommen. Es ergibt sich
hier ein Wert von
kB = (1,31 ± 0,09) · 10−23
J
.
K
(4.1)
J
Vergleicht man dieses Ergebnis mit dem Literaturwert von kB = 1,38 · 10−23 K
[8], so ergibt sich eine Abweichung von lediglich 5%. Im Rahmen der Messungenauigkeit konnte
der Literaturwert bestätigt werden. Da im Versuch die Temperatur lediglich geschätzt und
nicht gemessen wurde, könnte hier eine vermeintliche Fehlerquelle liegen, welche zu der wenn auch nur geringen - Abweichung nach unten führt.
Ebenso erwarten wir aufgrund der Tatsache, dass für sehr kleine bzw. sehr große Widerstände und Bandbreiten der Wert nicht mehr ganz korrekt ist, eine bestmögliche Bestimmung der Boltzmann-Konstante für mittlere Bandbreiten und mittlere Widerstände.
Diese Vermutung spiegelt sich auch in unseren Messwerten wider, so treffen beispielsweise die berechneten Werte der Boltzmann-Konstante für einen mittleren Widerstand
von Rin = 10 kΩ und mittlere Bandbreiten von ∆f1 = 3,3 kHz bzw. ∆f2 = 10 kHz mit
J
J
kB,1 = (1,37 ± 0,04) · 10−23 K
bzw. kB,2 = (1,38 ± 0,02) · 10−23 K
den Literaturwert sehr
exakt. Die Fehler der beiden berechneten Werte ergeben sich dabei aus der Fehlerfortpflanzung, wobei der Fehler des Eingangswiderstands gemäß Herstellerangaben jeweils 1% des
tatsächlichen Wertes beträgt6 [2].
Weiter wirft die Tatsache, dass sich für hohe bzw. niedrige Bandbreiten und Widerstände
abweichende Werte ergeben, die Frage auf, ob die Werte tatsächlich als statistisch verteilt gewertet werden können. Die stochastische Unabhängigkeit der Messwerte war die
Rechtfertigung für die Abweichung des in Gleichung (4.1) berechneten Wertes anhand der
Standardabweichung. Da wir hier jedoch annehmen, dass die Abweichungen in guter Näherung in beide Richtungen in etwa gleich gewichtet sind, können die Werte hier dennoch in
guter Näherung als statistisch verteilt angesehen werden und die Messung als Bestätigung
des Literaturwertes deuten.
6
Eine Ausnahme ist der Widerstand Rin = 1 MΩ, hier beträgt der relative Fehler nur 0,1%.
16
4 Ergebnisse und Diskussion
4.2 Schrot-Rauschen und Bestimmung der Elementarladung e
Wie bereits in Abschnitt 3 erläutert, wird das Schrot-Rauschen an einer Photodiode vermessen, wobei durch die Photodiode stets ein Photostrom IPh fließt. Gemäß Gleichung
(2.8) sollte hier
Zusammenhang resultieren. Die erhaltenen Messwerte für den
D ein linearer
E
2
Rauschstrom ∆I (t) in Abhängigkeit des Photostroms sind in Abbildung (4.3) dargestellt. Der lineare Zusammenhang konnte dabei für alle Bandbreiten verifiziert werden.
Aus der Steigung der Geraden lässt sich schließlich die Elementarladung e berechnen. Hierfür wird analog zur Berechnung der Boltzmann-Konstante in Abschnitt 4.1 Gleichung
(2.8) nach der Elementarladung umgeformt und man erhält für jeden Messwert einen Wert
für die Elementarladung. Auch hier nehmen wir die Messwerte als unkorreliert an und
erhalten deshalb einen Mittelwert mit Standardabweichung von
e = (−1,59 ± 0,20) · 10−19 C.
(4.2)
Auch hier stimmt der Wert sehr gut mit dem Literaturwert von e = −1,60 · 10−19 C [9]
überein, die relative Abweichung beträgt weniger als 1%. Dennoch ist der von uns berechnete Wert mit einem recht hohen Fehler behaftet. Dies rührt wie schon in Abschnitt 4.1
−19
x 10
A2
2.5
∆ f = 3,3 kHz
∆ f = 10 kHz
∆ f = 33 kHz
∆ f = 100 kHz
1.5
1
D
∆I (t)
2
E
/
2
0.5
0
0
2
4
IP h
6
/
8
10
µA
Abbildung 4.3: Die AbbildungD zeigt die
E Messwerte für den an der Photodiode gemessenen
2
Rauschstrom ∆I (t) in Abhängigkeit des Photostromes IPh für verschiedene Bandbreiten. Der erwartete lineare Zusammenhang konnte dabei bestätigt werden.
4.3 Bestimmung des absoluten Temperaturnullpunkts anhand des
Johnson-Rauschens
17
aus der Tatsache, dass für hohe bzw. niedrige Bandbreiten und Photoströme Störquellen
die Messwerte stärker verfälschen können als für mittlere Bandbreiten und Photoströme.
Dies scheint für hohe Bandbreiten und Photoströme insbesondere dadurch einleuchtend,
dass die Wirkung des RC-Tiefpasses aus Eingangswiderstand und Kapazität der Kabel
aufgrund des hohen Eingangswiderstand Rin = 10 kΩ nicht mehr unbedingt vernachlässigbar ist. Wir wollen von daher einen zweiten Wert für die Elementarladung gewinnen,
indem nur die Bandbreiten ∆f = 10 kHz und ∆f = 33 kHz sowie Photoströme im Bereich
von IPh ≈ 30 − 60 µA berücksichtigt werden. Es ergibt sich e = (1,626 ± 0,026) · 10−19 C
was mit einer Abweichung von 1,5% ebenfalls den Literaturwert wiedergibt, jedoch nun
eine deutlich kleinere Unsicherheit liefert.
Zweifellos kann die Messung sehr genau den Literaturwert bestätigen.
4.3 Bestimmung des absoluten Temperaturnullpunkts anhand des
Johnson-Rauschens
Im letzten Versuchsteil soll schließlich noch die Temperaturabhängigkeit des JohnsonRauschens bestimmt werden, die gemäß der Nyquist-Formel ebenfalls linear ist. Wie
bereits in Abschnitt 3 erläutert, wird hierzu die Rauschspannung an externen Widerstän−12
2
∆ f = 1 kHz
∆ f = 3,3 kHz
∆ f = 10 kHz
1.5
1
D
UJ (t)
2
E
/
V2
2.5
x 10
0.5
0
0
100
200
T
/
300
400
K
Abbildung 4.4: Die Abbildung zeigt den linearen Zusammenhang zwischen Rauschspannung und Temperatur für einen Eingangswiderstand von Rin = 10 kΩ bei
verschiedenen Bandbreiten.
18
4 Ergebnisse und Diskussion
−11
x 10
1
D
UJ (t)
2
E
/
V2
∆ f = 1 kHz
∆ f = 3,3 kHz
∆ f = 10 kHz
0
0
100
200
T
/
300
400
K
Abbildung 4.5: Die Abbildung zeigt den linearen Zusammenhang zwischen Rauschspannung und Temperatur für einen Eingangswiderstand von Rin = 100 kΩ bei
verschiedenen Bandbreiten.
den vermessen, welche in ein Dewar mit flüssigem Stickstoff abgesenkt
D werden
E können, um
2
sie zu kühlen. Es konnte dabei das Abfallen der Rauschspannung UJ (t) bei sinkender
Temperatur beobachtet werden. Die Messwerte der beiden Widerstände Rin = 10 kΩ und
Rin = 100 kΩ bei Raumtemperatur und Siedetemperatur von Stickstoff wurden in einem
Diagramm aufgetragen und eine Gerade durch die beiden Punkte gelegt. Dies ist in Abbildung (4.4) für Rin = 10 kΩ und in Abbildung (4.5) für Rin = 100 kΩ gezeigt. Auch
hier wurde der zuvor bestimmte Offset berücksichtigt und von der gesamten gemessenen
Rauschspannung subtrahiert. Dass die Messwerte tatsächlich den erwarteten linearen Zusammenhang liefert zeigt sich, indem die Nullstelle der Gerade bestimmt wird. Diese sollte
beim absoluten Temperaturnullpunkt T0 = 0 K liegen. Berechnet man die Nullstelle von
allen sechs Geraden und bildet deren Mittelwert, der mit der Standardabweichung behaftet
ist, so ergibt sich ein Wert von
T0 = (−1,0 ± 2,8) K,
was den erwarteten Wert im Rahmen der Messunsicherheit bestätigt.
(4.3)
19
4.4 Fazit
4.4 Fazit
In allen drei Versuchsteilen konnten die im Grundlagenteil (Abschnitt 2) erörterten Zusammenhänge sowohl qualitativ als auch quantitativ verifiziert werden, was insbesondere
dadurch erstaunlich ist, da die Versuchsapparatur sehr anfällig auf mechanische Vibrationen oder externe Störfelder durch z.B. Handys ist. Diese Sensibilität konnte anhand stark
fluktuierender Werte der Rauschspannung bei massiver mechanischer Erschütterung bzw.
unmittelbarer Nähe eines eingeschalteten Handys zur Versuchsapparatur beobachtet werden.
Nichtsdestotrotz konnten während des Experiments lediglich kleine Schönheitsfehler, wie
z.B. das Auftreten eines zusätzlichen RC-Tiefpasses aufgrund der Kapazität der Kabel,
was in Abschnitt 4.1 diskutiert wurde, beobachtet werden. Für eine genauere Analyse, wie
stark solche Fehler die Messwerte verfälschen wären weiterführende, deutlich aufwendigere
Messungen von Nöten, die an dieser Stelle nicht durchgeführt wurden.
Generell konnten die Phänomene des Rauschens als hervorragende Möglichkeit zur quantitativen Bestimmung der Boltzmann-Konstante kB und der Elementarladung e bestätigt
werden.
Abbildungsverzeichnis
20
Literatur
[1] Pfeifer, H.: Elektronisches Rauschen - Teil 1 Rauschquellen. Teubner-Verlag, 1959.
[2] Baak, David van, Geroge Herold und Jonathan Reichert: Noise Fundamentals
NF1-A Instructor’s Manual. TeachSpin Inc., 2495 Main Street, Suite 409, Buffalo, NY,
2010.
[3] Nyquist, H.: Thermal Agitation of Electric Charge in Conductors. Phys. Rev., 32:110–
113, July 1928.
[4] Johnson, J.B.: Thermal Agitation of Electricity in Conductors. Phys. Rev., 32:97–109,
July 1928.
[5] TeachSpin Inc.: SPLIA1-A Signal Processor / Lock-In Amplifier, 2009.
[6] Demtröder, Wolfgang: Experimentalphysik 2 - Elektrizität und Optik. Springer,
2009.
[7] Wikipedia, freie Enzyklopädie: Operationsverstärker, 31.01.2014.
[8] Nolting, Wolfgang: Grundkurs Theoretische Physik 4: Spezielle Relativitätstheorie,
Thermodynamik. Springer, 2010.
[9] Nolting, Wolfgang: Grundkurs Theoretische Physik 3: Elektrodynamik. Springer,
2007.
Abbildungsverzeichnis
2.1
2.2
2.3
2.4
4.1
4.2
4.3
4.4
4.5
Abhängigkeit der Rauschdichte von der Frequenz - weißes und rosa Rauschen 5
Schaltpläne und Durchlasskurven von RC-Hoch- und Tiefpass, sowie einer
möglichen Realisierung eines Bandpass . . . . . . . . . . . . . . . . . . . . . 7
Schaltplan des verwendeten Operationsverstärkers . . . . . . . . . . . . . . . 8
Schaltplan zur Messung des Johnson-Rauschens
D . . E. . . . . . . . . . . . . 9
Gemessene Abhängigkeit der Rauschspannung UJ (t)2 des Johnson-Rauschens
von der Bandbreite ∆f . . . . . . . . . . . . .D. . . . E. . . . . . . . . . . . . 13
Gemessene Abhängigkeit der Rauschspannung UJ (t)2 des Johnson-Rauschens
vom Widerstand Rin . . .D. . . . E
. . . . . . . . . . . . . . . . . . . . . . . . 14
2
Gemessener Rauschstrom ∆I (t) in Abhängigkeit des Photostromes IPh
16
Abhängigkeit von Rauschspannung und Temperatur für Rin = 10 kΩ . . . . 17
Abhängigkeit von Rauschspannung und Temperatur für Rin = 100 kΩ . . . 18