Übung Kostenrechnung SS 2014 - Technische Universität München
Werbung

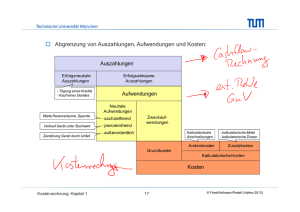
Technische Universität München Übung Kostenrechnung SS 2015 Übung 10 Break-Even-Analyse Technische Universität München Zielsetzung und Annahmen von Break-Even-Analysen Zielsetzungen: Ermittlung der Gewinnschwelle Kritische Menge Sensitivität des Gewinnes bei Absatzänderung Sensitivitätsanalyse, Grenzgewinn durch Ableitung Anlagenbeschaffung und -belegung kapitalintensiv und automatisiert vs. niedrige fixe aber hohe variable Kosten Kostenstrukturrisiko Verhältnis Fixkosten zu variablen Kosten, Operating Leverage Entscheidungsunterstützung bei Insourcing versus Outsourcing Annahmen des Grundmodells: Kosten und Erlöse hängen ausschließlich von der Ausbringungsmenge ab. Andere Einflussgrößen (bspw. Lohnkosten- und Preisänderungen) bleiben unberücksichtigt. Linearer Verlauf von Kosten und Erlösen innerhalb der betrachteten Mengen. Sprünge in den Kosten, z.B. durch notwendige Kapazitätserweiterungen, erfordern eine erweiterte Version der Break-Even-Analyse. Variable Kosten, fixe Kosten und Verkaufspreise werden als bekannt und konstant angenommen. Das Unternehmen maximiert den Gewinn und lässt einen etwaigen Zeitwert des Geldes durch unterschiedliche Zahlungszeitpunkte unberücksichtigt. Kostenrechnung: Kapitel 7 2 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München Break-Even-Analysen bei einem Produkt Ausgangsgleichung für Gewinn und Deckungsbeitrag Ermittlung Gewinn = Erlös – variable Kosten – Fixkosten = Deckungsbeitrag – Fixkosten Gesamtkosten-Umsatzmodell Erlöse/ Kosten G = p • x – kv • x – Kf = d • x – Kf mit: G p kv x Kf d Break-EvenPunkt = Gewinn = konstanter Stückpreis = konstante variable Stückkosten = Ausbringungsmenge = Fixkosten = Stückdeckungsbeitrag Gewinnzone Gesamtkosten K(x) K f kv x Verlustzone x Kostenrechnung: Kapitel 7 3 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München Aufgabe 10.1: Break-Even-Analyse Die Firma Expresso produziert Kaffeekapseln für Kaffeemaschinen. Die Kapseln werden in Stangen (Inhalt je Stange: 10 Kapseln) für 3,50 € je Stange verkauft. Die variablen Materialkosten belaufen sich auf 0,80 €, die variablen Fertigungskosten auf 0,20 € je Stange. Monatlich fallen fixe Kosten in Höhe von 1.250.000 € an. Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München a) Berechnen Sie die monatliche Break-Even-Menge sowie den monatlichen BreakEven-Umsatz. Was sagt die Break-Even-Menge inhaltlich aus? Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München b) Expresso will einen monatlichen Gewinn von 250.000 € erzielen. Welche Verkaufsmenge ist dafür pro Monat notwendig? Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München c) Unterstellen Sie, dass der Absatz in Höhe der in Teilaufgabe 3.2 berechneten Menge kontinuierlich über den Monat verteilt ist. Nach wie vielen Tagen wird die Break-Even-Menge erreicht (Annahme: 1 Monat = 30 Tage)? Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München d) Expresso plant eine neue Werbekampagne mit einem großen Hollywood-Star. Die fixen Kosten erhöhen sich dadurch pro Monat um 150.000 €, die Absatzmenge bleibt konstant auf dem Wert aus Teilaufgabe 3.2. Welchen neuen Verkaufspreis muss Expresso pro Stange verlangen, um weiterhin einen monatlichen Gewinn von 250.000 € zu erzielen? Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München e) Nehmen Sie nun an, dass Expresso die Werbekampagne nicht durchführt und die Stangen weiterhin zu einem Preis von 3,50 € verkauft. Jedoch muss der Gewinn mit einem Steuersatz von 20% versteuert werden. Welche Verkaufsmenge ist pro Monat notwendig, um weiterhin einen monatlichen Gewinn nach Steuern von 250.000 € zu erzielen? Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München Aufgabe 10.2: Break-Even-Analyse Ihr Nachbar Peter Drucker hat sich mit der Herstellung von bedruckten T-Shirts selbstständig gemacht. Da er von Ihnen weiß, dass Sie sich in den letzten Monaten intensiv mit Themen der Kostenrechnung auseinandergesetzt haben, bittet er Sie um Ihre Unterstützung bei einer Break-Even-Analyse. Peter Drucker verkauft jedes T-Shirt für 20,- €. Seine variablen Materialkosten belaufen sich auf 4,- €, die variablen Fertigungskosten auf 1,- € je T-Shirt. Jährlich fallen fixe Kosten in Höhe von 72.000 € an. Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München a) Berechnen Sie die Break-Even-Menge sowie den Break-Even-Umsatz. Was sagt die Break-Even-Menge inhaltlich aus? Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München b) Peter Drucker möchte eine Umsatzrendite von 15% erzielen. Welche Menge an verkauften T-Shirts ist dazu notwendig? Welchen Gewinn erzielt Peter Drucker bei dieser Verkaufsmenge? Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München c) Unterstellen Sie nun, dass Peter Drucker einen Gewinn mit einem Steuersatz von 35% versteuern muss. Welche Verkaufsmenge ist notwendig, um einen Zielgewinn nach Steuern von mindestens 20.000 € zu erzielen? Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013) Technische Universität München d) Welche Auswirkung haben generell folgende Sachverhalte auf die Break-EvenMenge: Steigerung der variablen Kosten je Stück, Senkung des Steuersatzes für Gewinne? Übung Kostenrechnung 2010) © Friedl/Hofmann/Pedell (Vahlen 2013)