Aufbau von Atomen
Werbung

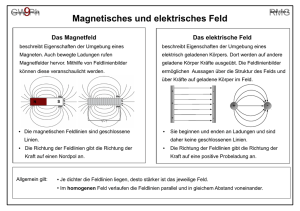
Aufbau von Atomen Ein Atom besteht aus einem positiv geladenen Atomkern und einer negativ geladenen Atomhülle. – – Träger der positiven Ladung sind Protonen, Träger der negativen Ladung sind Elektronen. – – – Atomhülle –– – + – – – – – – Für ein neutrales Atom gilt: Anzahl der Protonen = Anzahl der Elektronen Atomkern Aufbau von leitenden Stoffen Im Metall sind die positiv geladenen Atomrümpfe unbeweglich. Der Stromfluss kommt durch bewegliche Elektronen zustande. Atomrumpf Elektron Der Bandgenerator kleine Metallkugel große Metallkugel Gummiband Plastikbürste Kurbel Ladungstrennung erfolgt, wenn sich zwei unterschiedliche Nichtmetalle berühren. Tuch vor der Berührung Plastikstab Tuch Tuch während der Berührung Plastikstab Plastikstab Es werden Elektronen zwischen Tuch und Plastikstab + ausgetauscht + + – – – – – + nach der Berührung Tuch und Plastikstab sind ungeladen + + + + + ++ + + + + + + ++ + + Elektronenmangel (+) – – – – – – –– –– – –– – – –– –– – –– Elektronenüberschuss (–) Tuch und Plastikstab sind geladen. Aufbau einer Gewitterwolke 14 km Eiskristalle −− Warme, feuchte Luft steigt nach oben. 12 km 10 km 8 km 6 km 4 km 2 km + + + ++ ++ + + + + + + +++ + – ++ – – + ––– –– – – – –– – – – –– – – –– – – –– – – – – + + + – 40°C −− Es bilden sich Wassertropfen, Eiskristalle und Hagelkörner. –10°C −− Durch das schnelle Aufsteigen von Luft mit Wassertropfen und das Herabfallen schwerer Hagelkörner kommt es zur Ladungstrennung. 0°C +10°C Erdoberfläche Ladungsausgleich in Form von Blitzen + + + + + – – – – –– + + + + + + + + + + + + – –– – – – – – + + – – –– – – – – – – – – Länge von Blitzen: meist 2 – 3 km Dicke von Blitzen: meist 10 – 20 cm Dauer von Blitzen: etwa 1/1000 s Das elektrische Feld Ein elektrisches Feld existiert im Raum um elektrisch geladene Körper, in dem auf andere elektrisch geladene Körper Kräfte ausgeübt werden. + – + – + – + – Das elektrische Feld + _ + _ + – + + + + + – –– – – Kondensator als Ladungs- und Energiespeicher Auf den Platten eines Kondensators wird Ladung gespeichert. Die Speicherfähigkeit für Ladung wird durch die Kapazität C gekennzeichnet: C= C= Q– + + + Q } U A ε0 · εr · } d d Q+ + (für einen Platten­ kondensator) + U Die im elektrischen Feld des Kondensators gespeicherte Feldenergie E hängt von der Ladung Q der Platten und der Spannung U zwischen den Platten ab: E = }12 Q · U E=} 12 C · U 2 Analogien zwischen Gravitationsfeld und elektrischem Feld Gravitationsfeld Elektrisches Feld m q+ FG FE negativ geladene Platte Erdoberfläche Gravitationskraft: FG = m · g elektrische Kraft: FE = q · E Energie: Epot = m · g · h Energie: Epot = q · E · s m · g · h q · E · s ­Potenzial: V = } = g · h m ­Potenzial: φ = } q = E · s Potenzialverlauf um eine Masse Potenzialverlauf um eine ­Ladung V φ Masse m φ ~ }1r V ~ }1r r Ladung q r Bewegung geladener Teilchen in elektrischen Feldern In homogenen elektrischen Feldern wirkt auf geladene Teilchen eine konstante Kraft längs der Feldlinien: F = Q ∙ E Bewegung längs der Feldlinien (Längsfeld) Bewegung senkrecht zu den Feldlinien (Querfeld) + – + – – + – Geladene Teilchen werden beschleunigt oder abgebremst. Geladene Teilchen werden abgelenkt. Magnete und ihre Eigenschaften Magnete sind Körper, die andere Körper aus ferromagnetischen Stoffen (Eisen, Cobalt, Nickel) anziehen. Diese Stoffe sind magnetisierbar. unmagnetisches Eisen magnetisiertes Eisen Jeder Magnet hat mindestens zwei Pole (Nordpol, Südpol). gleichnamige Pole: Abstoßung Ungleichnamige Pole: Anziehung N S S N N S N S S N N S S N S N Bewegung geladener Teilchen in magnetischen Feldern In homogenen magnetischen Feldern wird auf bewegte geladene Teilchen eine Kraft ausgeübt. Bewegen sich die Teilchen senkrecht zu den Feldlinien, dann gilt: F = Q ∙ v ∙ B (Lorentzkraft) Für die geladenen Teilchen gilt die Linke-Hand-Regel: Magnetfeld zeigt in die ­Ebene hinein. Magnetfeld zeigt aus der ­Ebene heraus. Richtung des magnetischen Felds (N g S) Stromrichtung (von – nach +) Kraftrichtung – – Die Lorentzkraft wirkt bei v ⊥ B immer als Radialkraft. Damit gilt: 2 v Q ∙ v ∙ B = m ∙ } r und r=} m ∙ v Q ∙ B Geladene Teilchen im homogenen elektrischen Feld In einem homogenen elektrischen Feld wirkt auf geladene Teilchen eine konstante Feldkraft F = Q · E in Richtung der Feldlinien oder ent­ gegengesetzt zu ihnen. Im elektrischen Längsfeld (links) erfolgt ein Beschleunigen oder Abbremsen, im Querfeld (rechts) eine Ablenkung. U + – + – F + Q F – – d Positiv und negativ geladene Teilchen werden beschleunigt. Q · U = }12 m · v 2 – v + Positiv geladene Teilchen werden in Feldrichtung, negativ geladene Teilchen entgegengesetzt beschleunigt und damit abgelenkt. Geladene Teilchen im homogenen magnetischen Feld In einem homogenen magnetischen Feld wirkt auf bewegte geladene Teilchen eine Kraft senkrecht zur Bewegungsrichtung und senkrecht zur Richtung des Magnetfelds. Die Richtung der Ablenkung hängt auch von der Art der Ladung ab – v FL FL Magnetfeld in Blattebene hinein FL Der Betrag der Lorentzkraft kann mit folgender Gleichung berechnet werden: FL = Q · v · B FL – v FL FL Magnetfeld aus Blattebene heraus Die Richtung der Lorentzkraft ­ergibt sich mit der Linke-HandRegel. Elektrische Felder Ein elektrisches Feld existiert um elektrisch geladene Körper. Die Feldlinien verlaufen von + nach –. Die Richtung der Feldlinien gibt die Richtung der Kraft auf einen positiv geladenen Körper an. Die Feldlinien beginnen und e ­ nden an ­Ladungen. – + – + – – + + Die Stärke des elektrischen Felds wird mit der Größe elektrische Feldstärke E beschrieben: F E = U E = } } Q d V Einheit: ein Volt durch Meter (1 } m ) + + Ein elektrisches Feld besitzt ­Energie. Auf ein geladenes Teilchen wirkt die Feldkraft: F = Q · E F – Magnetische Felder Ein magnetisches Feld existiert um Permanentmagnete und um stromdurchflossene Leiter bzw. Spulen. Die Feldlinien verlaufen von Nord nach Süd. Die Richtung der Feldlinien gibt an, wie sich kleine Magnetnadeln im Feld ausrichten. Die Feldlinien sind geschlossene Linien. S N Die Stärke des magnetischen Felds wird mit der Größe magnetische Flussdichte B beschrieben: F B = } I · l N ) Einheit: ein Tesla (1 T = 1 } A · m – v FL Auf ein geladenes Teilchen wirkt die Lorentzkraft: FL = Q · v · B (v ⊥ B) Induktion in einem Leiter Elektromotorisches Prinzip Generatorprinzip l F F = B · l · I + l v – Ui = B · l · v Ui Bedingungen für das Entstehen einer Induktionsspannung Zeitlich konstantes Magnetfeld + – Ui Bewegung Zeitlich veränderliches Magnetfeld + – Ui Änderung der Stromstärke Alle Experimente zeigen: In einer Spule wird eine Spannung induziert, solange sich das von ihr umfasste Magnetfeld ändert. Selbstinduktion beim Ein- und Ausschalten Experiment 1 L1 Experiment 2 L2 L1 leuchtet später als L 2 auf. Beim Öffnen des Schalters leuchtet die Glimmlampe auf. Ein- und Ausschaltvorgang bei einer Spule I Einschalten I = konstant Ausschalten t U Ui = 0 t Induktionsherd –––––– Spule Glaskeramik ++++++ Magnetfeld Topfboden Die Maxwellgleichungen 1. In der Elektrostatik beginnen elektrische Feldlinien immer auf positiven Ladungen und enden auf negativen Ladungen 2. Magnetische Feldlinien sind geschlossen, Es gibt keine Quellen und Senken. 3. Eine Änderung der magnetischen Flussdichte, die eine Fläche durchsetzt, erzeugt ein elektrisches Wirbelfeld umdie Fläche herum. 4. Ein elektrischer Strom sowie eine zeitliche Änderung des elektrischen Felds, das eine Fläche durchsetzt, erzeugt um die Fläche ein magnetisches Wirbelfeld. R ε0 E dA = Σ Q R B dA = 0 R E ds = R –d B dA } d t µ0 Σ I + R d µ0 · ε0 · } E dA d t Induktion einer Wechselspannung homogenens Magnetfeld Ui }T4 }2T }34 T t In Spulen, die in einem homogenen magnetischen Feld gleichförmig rotieren, wird eine ­sinusförmige Wechselspannung induziert. Anwendungen des Induktionsgesetzes Induktion im zeitlich konstanten Magnetfeld (B = konstant) Induktion im zeitlich veränderlichen Magnetfeld (A = konstant) Anwendung: Generator Anwendung: Transformator Primärspule Sekundärspule Stator N1 N2 N Rotor S Ui U1~ ~U2 geschlossener Eisenkern aus Dynamoblechen