Testvorbereitung „Sinussatz/Kosinussatz“ - Mathematik

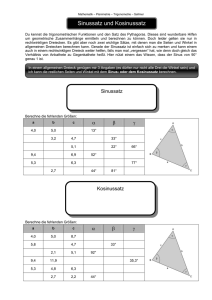
Dr. Fritsch, FGG
- Mathematik -
Klasse 10
Testvorbereitung „Sinussatz/Kosinussatz“
1.
1.1.
Gegeben sei ein beliebiges Dreieck ∆ durch die beiden Seiten = 3 und
Sinussatz
= 9 und den Winkel = 30°. Berechne die fehlende Seite und die fehlenden Winkel!
1.2.
Gegeben sei ein beliebiges Dreieck ∆ durch die beiden Seiten = 3 und
= 4 und den Winkel = 30°. Berechne die fehlende Seite und die fehlenden Winkel!
Gegeben sei ein beliebiges Dreieck ∆ durch die Seite = 5 und die beiden
Winkel = 70° und = 55°. Berechne die fehlende Seite und die fehlenden Winkel!
1.3.
1.4.
Gegeben sei ein beliebiges Dreieck ∆ durch die Seite = 6 und die beiden
2.
Kosinussatz
Winkel = 60° und = 100°. Berechne die fehlenden Seiten und den fehlenden Winkel!
2.1.
Gegeben sei ein beliebiges Dreieck ∆ durch die beiden Seiten = 6 und
= 8 und den Winkel = 20°. Berechne die fehlende Seite und die fehlenden Winkel!
Gegeben sei ein beliebiges Dreieck ∆ durch die drei Seiten = 3, = 6
und = 8. Berechne die fehlenden Winkel!
2.2.
3.1.
Ein Schiff peilt ein Seezeichen Z unter einem Winkel von 40° bezogen auf seine
(a)
Wie weit ist das Schiff jeweils zu den beiden Zeiten der Peilung vom Seezeichen Z
3.
Anwendungen
Fahrtrichtung an. Nach 6,0 liefert die Peilung einen Winkel von 65°.
entfernt? (Hinweis: Fertige eine Skizze an!)
(b)
Wie groß ist die minimale Entfernung zwischen Schiff und Seezeichen bei Weiterfahrt
Ein (gerader) kegelförmiger Sandhaufen bildet an der Spitze einen Winkel von 116°.
auf dem gleichen Kurs?
3.2.
Die Länge der Mantellinie beträgt 1,06. Welchen Durchmesser hat die Grundfläche des
Sandhaufens?
-1-
Dr. Fritsch, FGG
- Mathematik -
Klasse 10
Lösungen – Testvorbereitung „Sinussatz/Kosinussatz“
= 3 , = 9 , = 30°
1.
Sinussatz
1.1. gegeben:
Lösungsvorschlag:
=
→ sin =
∙ d.h. hier gibt es keine Lösung.
1.2. gegeben:
Lösungsvorschlag:
+
,
=
=
∙ +
,
=
, , gesucht:
, , = 1,5 > 1
'∙ ()°
(
= 3 , = 4 , = 30°
→ sin =
gesucht:
= 0,6667
-∙ ()°
(
41,8°
(Komplementärwinkel)
180° − 41,8° = 138,2°
41,8°
108,2°
Innenwinkelsumme: = 180° − 30° − 1
3=1
138,2°
11,8°
→ = arcsin 0,6667 = 1
=
,
+
→ =
1.3. gegeben:
Lösungsvorschlag:
=
=
,
+
,
+
=
=
+
=4
()°
( 5∙ 66,7°
()°
= 5,7
= 1,2
= 5 , = 70° , = 55°
= 180° − 70° − 55° = 55°
→ =
→ =
1.4. gegeben:
Lösungsvorschlag:
,∙ ( 5∙ 6)7,8°
∙ ∙ +
=
=
9 5∙ 99°
:)°
9 5∙ 99°
:)°
→ =
∙ ∙ +
=
=
; 5∙ ;)°
, , gesucht:
, , gesucht:
, , = 4,4
= 15,2
8)°
; 5∙ 6))°
8)°
gesucht:
= 4,4
= 6 , = 60° , = 100°
= 180° − 60° − 100° = 20°
→ =
(2 Lösungen)
= 17,3
2.
Kosinussatz
2.1. gegeben:
Lösungsvorschlag:
= 6 , = 8 , = 20°
= arccos
= arccos
= √ 8 + 8 − 2 ∙ cos = ?(6)8 + (8)8 − 2 ∙ 6 ∙ 8 ∙ cos 20° = 3,1
(, B CB C B )
(C8 )
(;B C(,6B C7B )
(C8∙(,6∙7)
= 40,7°
Innenwinkelsumme: = 180° − 20° − 40,7° = 119,3°
-2-
Dr. Fritsch, FGG
- Mathematik -
2.2. gegeben:
Lösungsvorschlag:
= arccos
= arccos
= 3, = 6 , = 8
(B C,B C B )
(C8, )
(, B CB C B )
(C8 )
Klasse 10
= arccos
= arccos
((B C;B C7B )
(C8∙;∙7)
(;B C(B C7B )
(C8∙(∙7)
gesucht:
= 18,6°
, , = 39,6°
Innenwinkelsumme: = 180° − 18,6° − 39,6° = 121,8°
3.
3.1.
Skizze:
Anwendungen
EEEEEE
gegeben:
=D
6 D8 = 6 , = < GD6 D8 = 40° ,
̅ = < GD8 I = 65° (Außenwinkel)
Z
S1
E
S2
EEEEE
EEEEE
=D
(a)
gesucht:
6 G , = D8 G
Lösungsvorschlag: = 180° − ̅ = 180° − 65° = 115° (Innenwinkel)
Sinussatz anwenden (Fall wsw):
Innenwinkelsumme: = 180° − 40° − 115° = 25°
,
+
=
=
(b)
gesucht:
Lösungsvorschlag:
sin =
LM
,
→
→ =
→ =
∙ +
∙ =
=
;J5∙ 669°
89°
;J5∙ -)°
89°
= 12,9 (1. Entfernung)
= 9,1
ℎ = EEEE
GI (Höhe auf c)
Anwendung des Sinus in einem rechtwinkligen Dreieck
ℎ = ∙ sin = 12,9 ∙ sin 40° = 8,3
(2. Entfernung)
(kürzeste Entfernung)
3.2. (Querschnitt des Sandhaufens = gleichschenkliges Dreieck)
gegeben:
= 116° , = = 1,06 (Mantellinie)
gesucht:
N (Durchmesser)
Lösungsvorschlag: (Anwendung des Kosinussatzes)
N = ?8 + 8 − 2 ∙ cos = ?(1,06)8 + (1,06)8 − 2 ∙ 1,06 ∙ 1,06 ∙ cos 116°
N = 1,80
-3-