Einführung in die Volkswirtschaftslehre 5. Übung
Werbung

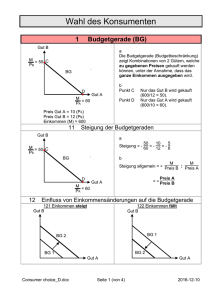
Einführung in die Volkswirtschaftslehre 5. Übung Wintersemester 2006/2007 Dipl.-Vw. Steffen Rätzel 5. Haushalts-, Produktions- und Kostentheorie 5.1 Mit Präferenzrelationen, Nutzenfunktionen und die dazugehörigen Annahmen hatten wir uns bereits beschäftigt. Die Begriffe Budgetgerade, Indifferenzkurve und Grenzrate der Substitution (GRS) spielen dabei eine wichtige Rolle. Erklären Sie die Begriffe. Welche Bedingung muss im HH-Optimum erfüllt sein? Die Budgetgerade ist der geometrische Ort aller Güterkombinationen, die für den Haushalt (HH) bei... Die Indifferenzkurve stellt alle Kombinationen der Mengen zweier Güter dar, die dem HH das gleiche... Der HH ist daher ................................. bei der Wahl der Güterbündel auf dieser Kurve. Die GRS ist - die Steigung der... - gibt an, wie viel man dem HH von Gut x geben muss, um ihn für den Verlust von... - Sie wird bestimmt durch GRS xy = y x 5.2 Zeichnen Sie die Indifferenzkurven zu folgenden Präferenzen, ermitteln Sie die GRS für jeden Fall, zeichnen Sie in jedes Diagramm eine Budgetbeschränkung und kennzeichnen Sie das Haushaltsoptimum: a) Ich trinke gern Rotwein aber niemals Weißwein b) Ich mag Rotwein und Weißwein, aber beide schmecken mir gleich gut c) Rotwein und Weißwein schmecken gemischt am besten d) Ich trinke nur eine Glas Rotwein, wenn ich auch ein Glas Weißwein trinken kann a) Weißwein Rotwein b) Weißwein Rotwein c) Weißwein Rotwein d) Weißwein Rotwein 5.3 Siegfried konsumiert nur Pizza und Cola (Pizza, Cola). Dabei liegen folgende alternativen Güterbündel auf einer Indifferenzkurve A = (1, 8); B = (2,4) und C = (3,2). a) Zeichnen Sie seine Indifferenzkurve (x-Achse Pizza, y-Achse Cola). b) Wie lautet die GRS zwischen A und B? a) 8 7 6 Bier 5 Cola 4 3 2 1 0 0 1 2 3 4 5 6 Pizza b) GRS: Für den Verzicht von einer Pizza (von 2 auf 1) genügen... 5.4 Lea verfügt über ein Einkommen von 750 Euro im Monat. Davon kauft Sie 5 Paar Schuhe. Da Sie von Schuhen allein nicht leben kann, konsumiert Sie zusätzlich Lebensmittel. Eine Einheit Lebensmittel kostet 10 Euro und ein paar Schuhe kosten 50 Euro. a) Zeichnen Sie Leas Budgetgerade und Ihre Indifferenzkurve. Lebensmittel Schuhe b) Das Schuhgeschäft in dem Lea immer ihre Schuhe kauft, unterbreitet ihr ein Angebot. Sie kann dort Mitglied werden. Für eine Mitgliedsgebühr von 200 Euro monatlich erhält sie alle Schuhe zu einem um 40 Prozent reduzierten Preis. Zeichnen Sie die neue Budgetgerade unter der Annahme, dass Lea das Angebot annimmt. c) Wird sich Lea für das Angebot entscheiden? d) Aufgrund der langen Kundenbindung bekommt Lea ein neues Angebot bei dem Sie nur noch 90 Euro als Mitgliedsbeitrag bezahlen muss. Wird Sie mit Sicherheit Mitglied werden? Wird sie (im Vergleich zu einer Nicht-Mitgliedschaft) jetzt mehr Schuhe kaufen oder weniger? Lebensmittel 75 50 5 15 In diesem Fall kann sie... Schuhe 5.5 Der Student Jack Brenner maximiert seinen Nutzen durch den Konsum von „Wodka Jelzin“ und „Schierker Feuerholz“. Seine Nutzenfunktion nimmt dabei folgende Form an U ( xW , xS ) = 4 xW xS − 5 . Der Preis für Wodka Jelzin beträgt 10 Euro und für Schierker Feuerholz 18 Euro. Jack hat ein Einkommen von 150 Euro in der Woche. a) Wie lautet die GRS für den Fall, dass Jack 3 Flaschen Wodka und 8 Flaschen Schierker trinken würde? Maximiert diese Zusammensetzung den Nutzen von Jack? ∂U ( xw , xs ) ∂xw = GRS = ∂U ( xw xs ) ∂xs Der Nutzen wird... b) Wie viel Flaschen Wodka und Schierker kauft Jack? Lösungsvorgehen: 1. Nutzenfunktion 2. Nebenbedingung (hier Budgetbeschränkung) 3. Langrange 4. Bedingung erster Ordnung 5. Berechnung 6. Ergebnis für xs einsetzen in (iii) xw* = 7 1 2 xs* = 4 1 6 1 1 Jack maximiert seinen Nutzen durch den Konsum von 7 Flaschen Wodka Jelzin und 4 Flaschen 2 6 Schierker Feuerholz. Bemerke: GRS = 4 ⋅ 71 2 = 4 ⋅ 41 6 5.6 Ein Unternehmen produziert seine Güter unter Einsatz von Kapital k und Arbeit l. Es besitzt die Produktionsfunktion: F ( k , l ) = 4 k 0 , 5l 0 , 4 a) Berechnen Sie das Grenzprodukt des Faktors Arbeit bei einem Faktoreinsatz von (4, 6). Interpretieren Sie das Ergebnis. b) Ist das Grenzprodukt fallend oder steigend im Faktor Arbeit? Was bedeutet das Ergebnis? Zur Bestimmung des Anstiegs des Grenzproduktes – bilde... c) Besitzt das Unternehmen fallende, steigende oder konstant Skalenerträge? Interpretieren Sie das Ergebnis. Skalenerträge sind Fallend Steigend wenn r = α + β Konstant 5.7 Erfried hat die Nutzenfunktion U(x, y) = 6xy + 4. Die Preise für beide Güter sind jeweils 1 € und sein Einkommen beträgt 30. Wie viel wird er von Gut x nachfragen? a) 6 b) 15 c) 30 d) Keine der Antworten ist korrekt 5.8 Tims hat die Nutzenfunktion U(x, y) = x4y. Angenommen Gut x kostet 3 Euro und Gut y kostet 2 Euro, so wird Tims Budgetgerade eine seiner Indifferenzkurven tangieren, wenn: a) 3x = 2y b) 4x = 2y c) 8y = 3x d) xy = 3/2 5.9 Ein Unternehmen produziert seine Güter unter Einsatz von zwei Inputfaktoren. Wenn sich die Kosten beider Faktoren verdoppeln: a) ändert sich das kostenminimale Faktoreinsatzverhältnis b) bleibt die Faktornachfrage konstant c) bleibt das kostenminimale Faktoreinsatzverhältnis konstant d) ohne weiter Informationen können wir keine Aussage treffen 5.10 Ein Unternehmen setzt für seine Produktion nur Arbeit ein. Das Grenzprodukt der Arbeit lautet GP = 200 − 0,8l . Der Preis für das verkaufte Produkt liegt bei 4,50 Euro und der Lohnsatz beträgt 15 €. Der Grenzerlös ergibt sich aus: a) 200 – 3,6l b) 1000 – 3,6l c) 185 – 0,8l d) 985 – 3,6l