(P/R = Lehrbuch Pindyck/Rubinfeld)

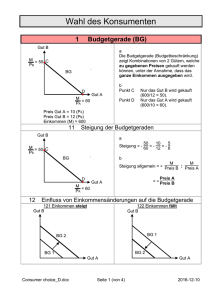
Dr. M. Ruiz HWI-B.Sc. WS1011 Fragen zur Vorl. vom 6.1.11 Seite 1 von 5 Seiten.
Frage 76
Nehmen Sie an, ein HH sieht Jever und Astra als vollkommene Substitute an (Sie mögen das völlig
anders beurteilen, aber Nutzen ist ein individuelles Konzept!), die er, unabhängig von seinen
Versorgungsniveaus, immer genau im Verhältnis 1:1 substituiert, ohne Nutzeneinbußen zu erleiden.
a) Zeichnen Sie eine Schar von Indifferenzkurven, die diese Präferenzendes HH beschreiben.
(Achtung: Es handelt sich hier nicht um den Normalfall konvexer Indifferenzkurven, sondern um einen
sehr seltenen Sonderfall!!)
b) Beschreiben Sie die Form seiner Indifferenzkurven.
Wie kann man die Form von Indifferenzkurven ganz allgemein beschreiben?
Was versteht man unter der Grenzrate der Substitution? Studieren Sie dazu die Abschnitte 3.1.5,
3.1.6 und 3.1.7 im Lehrbuch von Pindyck/Rubinfeld.
Wie groß ist die Grenzrate der Substitution (GRS) im obigen Beispiel?
c) Welchen optimalen Warenkorb aus Jever und Astra wird der HH mit einem Budget von Euro 20,wählen, wenn 1 Flasche Jever Euro 2,- kostet und 1 Flasche Astra Euro 1,- ? (Grafische Analyse der
nutzenmaximalen Konsumentscheidung im x1-x2-Diagramm).
( Auch dies ist ein Sonderfall, wie Sie mit Hilfe der Zeichnung erkennen: Das Optimum ist hier kein
Tangentialpunkt von Budgetgerade und höchster Indifferenzkurve, die Marginalbedingung für das
Optimum aus dem Langrange Ansatz ist nicht erfüllt. Es handelt sich um eine sog. Randlösung, bei
der die Marginalbedingung nicht gilt. (Lösung: 20 Flaschen Astra) (Vgl. P/R Kap. 3.3.1. Randlösungen)
Frage 77
a) Erläutern Sie den Begriff der `Grenzrate der Substitution´ (GRS) für einen Punkt auf der
Indifferenzkurve. (grafische, algebraische und verbale Lösung: Also drei unterschiedliche Lösungen!!)
b) Leiten Sie den Zusammenhang zwischen der GRS und dem Verhältnis der Grenznutzen der beiden
Güter algebraisch her.
(Lösungshinweis: Nutzenfunktion total differenzieren. Entlang der Indifferenzkurve gilt U= konstant,
also dU = 0; Daraus lässt sich das Verhältnis von x1 zu x2 entlang der Indifferenzkurve ermitteln.
Auflösen ergibt GRS = | dx1/ dx2 | = (df /dx2) / (df /dx1)
Dies ist in der Vorlesung vorgeführt worden. Partielle Differentiation der Nutzenfunktion nach den
beiden Argumenten x1 und x2 und Ermittlung des Differentials der Nutzenfunktion dU für die
tatsächlichen Änderungen dx1 und dx2 .
Vgl. dazu Vorlesung und Sydsaeter/Hammond Kap12.9 S. 513. )
c) Für beide Güter möge jeweils das 1. Gossen´sche Gesetz der abnehmenden Grenznutzen gelten,
dh die Grenznutzen eines Gutes sinken mit zunehmender Gütermenge dieses Gutes und steigen mit
abnehmender Gütermenge dieses Gutes cet. par.
Erläutern Sie mit Hilfe des Ergebnisses aus (b), warum es danach entlang einer Indifferenzkurve in
Richtung der Abzisse zu einer sinkenden GRS |dx1/dx2| kommt. (mit Grafiken; Vgl Vorlesung).
d) Begründen Sie ökonomisch, warum Indifferenzkurven im Zwei-Güter-Diagramm eine negative
Steigung haben und warum Sie in der Regel konvex zum Ursprung gekrümmt sind. (die Steigung
ergibt sich aus dem Vorzeichen von dx1/dx2 = - (df /dx2) / (df /dx1) und damit aus den Vorzeichen
von df /dx2 > 0 und df /dx1 > 0 . Achtung: Normalerweise sind die Grenznutzen positiv und daher
haben die Indifferenzkurven eine negative Steigung. Wenn aber ein Gut von zwei Gütern
ausnahmsweise negative Grenznutzen aufweist (ein "Ungut") , wie zB Lärm oder auch die
Gütereigenschaft "Risiko s" für einen risikofeindlichen Anleger, dann lassen sich daraus
ausnahmsweise Indifferenzkurven mit positiver Steigung herleiten!!!
Ein risikoaverser Anleger hat also im E(x) - s(x) -Diagramm positiv geneigte Indifferenzkurven, ein
risikoneutraler Anleger hat horizontale Indifferenzkurve (er interessiert sich nicht für s , so wie ein
Hund sich nicht für Fisch interessiert) un ein risikoliebender Anleger hat normale negativ verlaufende
Indifferenzkurven, weil er sowohl E(x) als auch s(x) schätzt. (Vgl Frage 46 und 47c vom 14.11.08)
(siehe 70b; Um diesen Effekt klar zu erkennen, muß man aber ausnahmsweise das Vorzeichen von
dx1/dx2 betrachten, dass sich hinter dem als Absolutbetrag definierten GRS verbirgt!)
e) Erläutern Sie, warum die Punkte auf einer Linearkombination zwischen einem Punkt auf einer
bestimmten Indifferenzkurve U0 ganz links und einem Punkt auf der gleichen Indifferenzkurve ganz
rechts immer auf höheren Indifferenzkurven als U0 liegen müssen, wenn die Indiffenzkurven konvex
zum Ursprung gekrümmt sind.
f) Die GRS |dS/dM| eines typischen Opel-Käufers zwischen den Eigenschaften "Styling" S und
"Motorleistung" M sei sehr klein. Erläutern Sie, was das für den Hersteller bedeutet. (Vgl. Beispiel 3.1
aus P/R , S. 115f.)
Frage 78 a) Erläutern Sie, warum im Haushaltsoptimum eines HH seine individuelle GRS |dx1/dx2|
gerade so groß sein in muss, wie die Opportunitätskosten des Konsums einer zusätzlichen Einheit von
Gut 2 bei den herrschenden Marktpreisen (p2/p1).
Dr. M. Ruiz HWI-B.Sc. WS1011 Fragen zur Vorl. vom 6.1.11 Seite 2 von 5 Seiten.
b) Wie interpretiert man die Optimalitätsbedingung in der Form f´2/p2 = f´1/p1 ?
(Lösungshinweis: Der Grenznutzen einer zusätzlichen Geldeinheit muß im Optimum bei Verwendung
für Gut 1 genau so groß sein wie bei Verwendung für Gut 2. Diese Bedingung wird bezeichnet als 2.
Gossen´sches Gesetz)
( zb. f´2/p2 =(df/dx2)/p2 = der zusätzliche Nutzen einer zusätzlichen kleinen Mengeneinheit von x2
(Dimension: Nutzeneinheiten pro Mengeneinheit) bezogen auf den Preis für eine (zusätzliche)
Mengeneinheit von x2 (Dimension: Geldeinheiten pro Mengeneinheit) = Grenznutzen einer zusätzlich
für Gut 2 ausgegebenen Geldeinheit (Dimension: Nutzeneinheiten pro Geldeinheit) Dies wird auch
bezeichnet als "Grenznutzen einer Geldeinheit in der Verwendung für Gut 2" .
Studieren Sie dazu P/R Abschn. 3.5 . Ist in der Vorlesung erläutert worden!)
Frage 79 (Zu dieser Frage studieren Sie Abschn. 3.3 P/R. )
Ein HH befindet sich in einem bestimmten Punkt B auf seiner Budgetgeraden und stellt in dieser
Situation mit Erstaunen fest, dass seine Grenzrate der Substitution von Gut 1 durch Gut 2 in diesem
Punkt B wesentlich größer ist als das mengenmäßige Tauschverhältnis (Opportunitätskosten) dieser
Güter auf dem Gütermarkt (p2/p1). (Lösungshinweis: P/R Abb. 3.13, S .128)
a) Geben Sie jeweils eine genaue inhaltliche Erläuterung der Begriffe "GRS" und
"Opportunitätskosten", und erklären Sie, wie genau der HH den oben genannten Größenunterschied
praktisch erkennen kann. Bedenken Sie bei Ihrer Erklärung: Nur wenige Konsumenten haben VWL
studiert und finden doch ihr Konsumoptimum, ohne eine Lagrange-Funktion differenzieren zu
können!!!
b) Untersuchen Sie, ob sich der HH oben gerade in seinem Optimum befindet, links davon oder rechts
davon? (mit Zeichnung und Erläuterungen)
c) In welche Richtung auf der Budgetgeraden wird der HH sich vernünftigerweise bewegen, wenn er
den oben genannten Unterschied zwischen seiner subjektiven GRS und den objektiven
Opportunitätskosten auf den Gütermärkten erkennt, aber nicht weiß, wo genau sein Optimum liegt?
(mit Begründung)
d) Erläutern Sie genau den Zähler, den Nenner und den Gesamtausdruck (df/dx1)/p1
(Lösungs-Hinweis: im Zähler steht der zusätzliche Nutzen einer zusätzlichen Mengeneinheit x1 mit der
Dimension Nutzeneinheit/Mengeneinheit; im Nenner steht der Preis einer zusätzlichen Mengeneinheit
mit der Dimension Euro/Mengeneinheit; der Gesamtausdruck (Mengeneinheiten kürzen sich heraus)
ist der zusätzliche Nutzen, den man mit einem zusätzlichen Euro erhält, wenn man diesen für das
Gut 1 ausgibt = Grenznutzen einer Geldeinheit für bei der Verwendung für Gut 1.)
e) Warum ist im Haushaltsoptimum eines HH sein Grenznutzen einer Geldeinheit bei Verwendung für
Gut 1 gleich seinem Grenznutzen einer Geldeinheit bei Verwendung für Gut 2 ? Was würde ein HH
tun, wenn sein Grenznutzen einer Geldeinheit z.B. bei Verwendung für Pullover größer wäre als bei
Verwendung für Hosen??? Was wäre das für eine Nutzensituation?
(Herleitung und praktische Erläuterung der Optimalbedingung: !!!! f´1/p1 = f´2/p2 Vgl. P/R Kapitel 3.5;
Der HH würde sein Budget umschichten, weil es noch nicht optimal ist und mehr Pullover aber
weniger Hosen kaufen)
Frage 80
Die Präferenzordnung eines HH sei beschrieben durch die Nutzenfunktion U = x11/2.x21/4 .
Die Güterpreise seien p1 = 12 und p2 = 12 .
a) Berechnen Sie die nutzenmaximalen Verbrauchsmengen für eine Konsumsumme e von
Euro 180,-. ( Hinweis: Optimalitätsbedingung aus dem Lagrange-Ansatz formulieren; Optimales
Güterkonsumverhältnis berechnen, indem man für die GRS das Verhältnis der Ableitungen
(Grenznutzen von Gut 2 zu Grenznutzen von Gut 1 bildet und gleich dem Verhältnis von Preis 2 zu
Preis 1 setzt. Die Lösung ergibt das optimale Verhältnis von x1 zu x2 .
Einsetzen des optimalen Güterverhältnisses in die Budgetgerade und Auflösen nach x1 bzw x2.
Ergebnis: x1 = 10 ; x2 = 5)
b) Wie verändern sich die Verbrauchsmengen im Haushaltsoptimum, wenn der Staat jedem
Verbraucher für Gut 2 pro Gütereinheit eine Beihilfe (Preissubvention) von Euro 6,- je ME zahlt?
(Hinweis: der Verbraucher zahlt jetzt also wegen der Subvention für Gut 2 nur noch p2 = 12- 6 = 6).
Neues Optimum bei: x1 = 10 ; x2 = 10 )
c) Wie hoch ist hier der insgesamt vom Staat zu zahlende Subventionsbetrag?
( Euro 60 : Optimale Verbrauchsmenge für Gut 2 mal Subventionsbetrag 10x6=60
Achtung: Der gesamte Subventionsbetrag hängt von der tatsächlich nachgefragten Menge x2 ab!)
d) Wie würde sich die Güternachfrage im HH-Optimum verändern, wenn der Staat dem HH den
ermittelten Subventionsbetrag aus c) nicht als Preissubvention gewährt hätte, sondern ihm statt
(
Dr. M. Ruiz HWI-B.Sc. WS1011 Fragen zur Vorl. vom 6.1.11 Seite 3 von 5 Seiten.
dessen (dh bei den alten Preisen p1 = 12 und p2 = 12 ) einen gleich großen Betrag als pauschale
Einkommenshilfe (allgemeine Einkommenssubvention) zukommen lassen würde?
(Ergebnis: dann ist e = 180 + 60 = 240 und im Optimum ist x1 = 13,33 ; x2 = 6,67 )
d) Untersuchen Sie rechnerisch, welche Art der Subventionierung der HH hier vorziehen wird.
(Einsetzen der jeweiligen Lösungen in die Nutzenfunktion : Ausrechnen: U(10;10) < U(13,33 ; 6,66)
Der HH zieht die pauschale Einkommenshilfe der Preisbeihilfe vor.)
Frage 81
a) Beschreiben Sie das allgemeine Haushaltsoptimum des HWI-Studenten Peter mit Hilfe einer Grafik.
b) Erläutern Sie das Konzept des "Grenznutzens des Geldes in alternativen Verwendungen" verbal
und mit Hilfe einer Formel. Der aktuelle Preis des eines Gutes, zB Kaviar, sei 5 Euro/gr, eine
Zunahme von 10gr auf 11gr wird von Peter in der aktuellen Situation als Nutzenzuwachs von 10
Nutzeneinheiten empfunden. Wie gross ist Peters Grenznutzen einer Geldeinheit bei einer
Verwendung für Kaviar in dieser Situation?
c) Wie groß muss Peters Grenznutzen einer Geldeinheit bei Verwendung für das zweite Gut
(Wollsocken) in der obigen Situation sein, damit Peter ganz sicher sein kann, sein Konsumoptimum
erreicht zu haben?
Frage 82
a) Zeigen Sie, wie sich für stufenweise steigendes Einkommen e1< e2< e3 .... bei gegebenen,
unveränderten Güterpreisen eine Folge von verschiedenen Haushaltsgleichgewichtspunkten im
x1-x2-Diagramm grafisch herleiten lassen. (Gleichgewichtspunkte des HH : hier Punkte der sog.
"Einkommens-Konsum-Kurve") (Hinweis: Zeichnung der sich durch e verschiebenden Budgetgeraden
und der sich jeweils ergebenden neuen Optimalpunkte. Mit vollständiger Bezeichnung aller Kurven
und relevanten Punkte). (Vgl. P/R 4.1.3 )
b) Die Nutzenfunktion eines Nachfragers sei mit U = x11/8x23/8 gegeben, die Güterpreise
seien p1 = 2 und p2 = 3 . Ermitteln Sie den Einfluß des Einkommensniveaus e auf die
Nachfragemenge nach Gut 1 und Gut 2, wenn der Nachfrager bei jedem Einkommen jeweils seinen
optimalen Konsumpunkt wählt. Beschreiben Sie die Zusammenhänge.
(Hinweis: Bestimmen Sie die nutzenmaximalen Verbrauchsmengen unter der Nebenbedingung
e = 2x1 + 3x2 für ein allgemeines Einkommensniveau e: Aus der Optimalitätsbedingung (Ergebnis
des Lagrange-Ansatzes) wird das optimale Güterverhältnis berechnet , in die Budetgleichung
eingesetzt und nach x1 bzw x2 aufgelöst. Ergebnis: x1 = (1/8).e ; x2 = (1/4).e ; Solche
Einkommens-Nachfrage-Kurven nennt man "Engel-Kurven" nach einem Statistiker Engel)
Frage 83
a) Zeigen Sie, wie sich bei schrittweiser Zunahme des Preises für Gut 1 1p1 < 2p1 < 3p1 ....eine
Folge von Haushaltsgleichgewichten im x1-x2-Diagramm grafisch herleiten lassen, wobei das
Einkommen e und der Preis p2 konstant bleiben. (Gleichgewichtspunkte des HH : hier Punkte der
sog. "Preis-Konsum-Kurve") (Zeichnung der sich um den Abzissenschnittpunkt drehenden
Budgetgeraden und der sich jeweils ergebenden Optimalpunkte. Mit vollständiger Bezeichnung aller
Kurven und relevanten Punkte) (Vgl. P/R 4.1.1. Preisänderungen)
b) Die Nutzenfunktion des HH sei wie oben wiederum U = x11/8 x23/8 , das Einkommen e= 100 und
p2 = 3. Ermitteln Sie den Einfluß des Preisniveaus p1 auf die Nachfrage des HH für das Gut 1, wenn
der HH jeweils seinen optimalen Konsumpunkt wählt. Erläutern Sie die Zusammenhänge.
(Hinweis: Bestimmen Sie die nutzenmaximalen Verbrauchsmenge für Gut 1 unter der
Nebenbedingung 100 = p1 x1 + 3x2 für ein allgemeines Preisniveau p1
Ergebnis: x1 = 25/p1 bzw p1 = 25/x1 ; Solche Preis-Nachfrage-Kurven kennen wir schon aus den
Marktanalysen, man nennt diese Kurven Marshall-Kurven nach einem Ökonomen Marshall. )
Frage 84
Wie groß ist die GRS für ein festes Güterverhältnis x1:x2 von 1:1 auf einer beliebigen Indifferenzkurve
der Nutzenfunktion U = 6x10,4x20,8 ? (GRS = 2)
(Hinweis: Die Güterniveaus x1 und x2 sind beliebig hoch, aber jeweils gleichgroß! Mit anderen Worten:
Es geht um alle Punkte, die auf einem Strahl aus dem Ursprung mit der Steigung 1 liegen.)
(Hinweis: Es handelt sich hier wieder um eine sog. Cobb-Douglas-Funktion mit besonderen
Eigenschaften: U = Ax1a x2b a,b sind positive Konstanten.
Die GRS ergibt sich natürlich wieder aus dem umgekehrten Verhältnis der Grenznutzen
(Absolutbetrag). Berechnen Sie die GRS. (Lösung: (b/a)(x1/x2) )
Die GRS auf beliebigen Indifferenzkurven ist nach dieser Lösung für Punkte, die auf einem Strahl aus
dem Ursprung liegen,konstant, weil dann x1/x2 konstant ist. Im obigen Fall ist die Grenzrate der
Substitution überall gleich (0,8/0,4) (1/1) = 2 )
Dr. M. Ruiz HWI-B.Sc. WS1011 Fragen zur Vorl. vom 6.1.11 Seite 4 von 5 Seiten.
Verwenden Sie diese schöne Eigenschaft, um 3 verschiedene Indifferenzkurven aus dieser Funktion
mit einigermaßen korrekten GRS mit Hilfe dreier Strahlen aus dem Ursprung in ein Diagramm zu
zeichnen! (Vgl. Vorlesung)
Frage 85
a) Gegeben seien die Preise p1 und p2 sowie das Einkommen e. Leiten Sie für eine Nutzenfunktion
vom Cobb-Douglas-Typ U = x1a. x2b mit den festen Koeffizienten a,b>0 nach Lagrange das
Haushaltsoptimum her und bestimmen Sie daraus die Güternachfragefunktionen des HH für x1 und für
x2. (Bestimmung der Bedingungen 1. Ordnung für ein Nutzenmaximum; Einsetzen in die
Budgetgleichung und Auflösen nach x1 bzw x2. Für diese Cobb-Douglas-Funktion des Typs
U = x1a x2b ergeben sich aus dem Lagrange-Ansatz die folgenden speziellen Nachfragefunktionen:
x1 = (e/p1)(a/(a+b)) und x2 = (e/p2)(b/(a+b))
Achtung: Diese Ergebnisse gelten nur für den Sonderfall dieser C-D-Nutzenfunktion!!! Man darf diese
Formel daher keinesfalls ohne ausführliche Prüfung und Herleitung verwenden!
b) Erläutern Sie die Auswirkungen von Änderungen von e auf x1 und auf x2. Wie groß sind die
Einkommenselastizitäten der Güternachfrage?
c) Erläutern Sie die Auswirkungen von Änderungen von p1 auf x1 und von p2 auf x2. Wie groß sind die
Preiselastizitäten der Güternachfrage?
d) Wie groß ist der Einfluß von p2 auf x1 und von p1 auf x2? Wie groß sind die Kreuzpreiselastizitäten
der Güternachfrage?
e) Überprüfen Sie Ihre Lösungen für Frage 84b und 85b mit Hilfe der Cobb-Douglas Nachfragefunktionen.
Frage 86
Zeichnen Sie die speziellen Indifferenzkurven (Skizze des jeweils typischen Verlaufes) für die
folgenden Präferenzen in jeweils ein x1-x2-Diagramm:
a) HH A ist der Auffassung, daß Gut 1 restlos durch Gut 2 ersetzt werden kann aber Gut 2 nicht
restlos durch Gut 1 ersetzt werden kann (Gut 2 ist nicht vollständig substituierbar).
(Man unterscheidet zwischen vollkommener Substitution (es liegt eine Indifferenzgerade (atypische
Indifferenzkurve) vor, nicht notwendig mit der Steigung -1) und vollständiger bzw nicht-vollständiger
Substitution. Diese zweite Eigenschaft bezieht sich auf die Frage, ob die Indifferenzkurven die x1Achse und/oder die x2-Achse erreichen oder eben nicht erreichen. Überlegen Sie einmal, für welche
beiden Güter eine vollständige Substitution nur einseitig gelingt. (x1 ist bei gegebenem Nutzenniveau
vollständig durch x2 substituierbar, aber x2 kann nicht vollständig durch x1 ersetzt werden!!!)
b) HH B isst einen Hamburger und spült ihn mit einem Bier herunter. Ohne eine weitere Einheit des
einen Gutes wird er keine weitere Einheit des anderen Gutes konsumieren. (Hinweis: Die
Indifferenzkurve von komplementären Gütern hat, genau genommen, nur einen effizienten Punkt:
Komplementäre Gütern lassen sich gegeneinander nicht substituieren.)
c) Hund Bello mag Wurst, interessiert sich aber nicht für Fisch. Skizzieren Sie seine Indifferenzkurven.
d) Kühlaggregate sind durch ein bestimmtes Verhältnis der Eigenschaften "Kühlleistung" und
"Lärmerzeugung" gekennzeichnet. Wie könnten die Indifferenzkurven (Iso-Nutzenlinien) eines Käufers
von Kühlaggregaten aussehen? ("Betriebslärm" ist ein sog. "Ungut". Die Abwesenheit von "Lärm"
kann als positive Eigenschaft "Laufruhe" aufgefaßt werden. Konstruieren Sie zunächst eine normale
Indifferenzkurve für die Güter "Kühlleistung" und "Laufruhe". Wie ändert sich die Indifferenzkurve,
wenn Sie statt "Laufruhe" auf der Achse "Betriebslärm" auftragen (die Richtung der Metrik auf der
Achse umdrehen) ?
Frage 87
Nehmen Sie an, ein HH sieht Jever und Astra als vollkommene Substitute an (Sie mögen das völlig
anders beurteilen, aber Nutzen ist ein individuelles Konzept!), die er, unabhängig von seinen
Versorgungsniveaus, immer genau im Verhältnis 1:1 substituiert, ohne Nutzeneinbußen zu erleiden.
a) Zeichnen Sie eine Schar von Indifferenzkurven, die diese Präferenzendes HH beschreiben.
(Achtung: Es handelt sich hier nicht um den Normalfall konvexer Indifferenzkurven, sondern um einen
seltenen Sonderfall!!)
b) Was versteht man unter der Grenzrate der Substitution? Wie groß ist sie im obigen Beispiel?
c) Welchen optimalen Warenkorb aus Jever und Astra wird der HH mit einem Budget von Euro 20,wählen, wenn 1 Flasche Jever Euro 2,- kostet und 1 Flasche Astra Euro 1,- ? (Grafische Analyse der
nutzenmaximalen Konsumentscheidung). ( Auch dies ist ein Sonderfall, wie Sie mit Hilfe der
Zeichnung erkennen: Das Optimum ist hier kein Tangentialpunkt von Budgetgerade und
Indifferenzkurve, die Marginalbedingung für dasOptimum aus dem Langrange Ansatz ist nicht erfüllt.
Es handelt sich um eine sog. Randlösung, bei der die Marginalbedingung nicht gilt.
Lösung: 20 Flaschen Astra) (Vgl. P/R Kap. 3.3.1. Randlösungen)
Dr. M. Ruiz HWI-B.Sc. WS1011 Fragen zur Vorl. vom 6.1.11 Seite 5 von 5 Seiten.
Frage 88 (Tutorium)
Untersuchen Sie, ob für allgemeine p1, p2 und e aus den drei unterschiedlichen Nutzenfunktionen a, b
und c jeweils die gleichen allgemeinen Gleichgewichte und damit auch identische
Nachfragefunktionen für Gut 1 einerseits und für Gut 2 andererseits herleitbar sind.
a) U = x1.x2
b) U = (x1.x2)0,5
c) U = ln(x1) + ln(x2)
ln ist der natürliche Logarithmus zur Basis e
(Lösung: In allen drei Fällen ergeben sich interessanterweise genau die gleichen EinkommensNachfragefunktionen und die gleichen Preis-Nachfragefunktionen!!! b und c sind monotone
Transformationen von a!)