Trigonometrie - toolcase.org

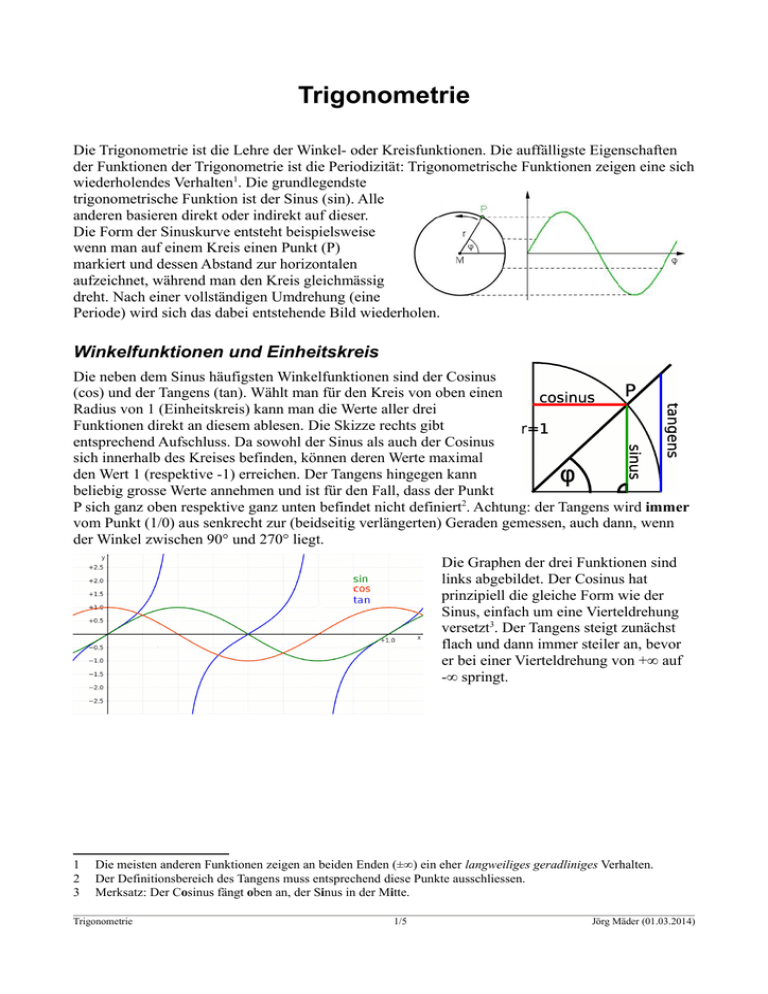
Trigonometrie
Die Trigonometrie ist die Lehre der Winkel- oder Kreisfunktionen. Die auffälligste Eigenschaften
der Funktionen der Trigonometrie ist die Periodizität: Trigonometrische Funktionen zeigen eine sich
wiederholendes Verhalten1. Die grundlegendste
trigonometrische Funktion ist der Sinus (sin). Alle
anderen basieren direkt oder indirekt auf dieser.
Die Form der Sinuskurve entsteht beispielsweise
wenn man auf einem Kreis einen Punkt (P)
markiert und dessen Abstand zur horizontalen
aufzeichnet, während man den Kreis gleichmässig
dreht. Nach einer vollständigen Umdrehung (eine
Periode) wird sich das dabei entstehende Bild wiederholen.
Winkelfunktionen und Einheitskreis
Die neben dem Sinus häufigsten Winkelfunktionen sind der Cosinus
(cos) und der Tangens (tan). Wählt man für den Kreis von oben einen
Radius von 1 (Einheitskreis) kann man die Werte aller drei
Funktionen direkt an diesem ablesen. Die Skizze rechts gibt
entsprechend Aufschluss. Da sowohl der Sinus als auch der Cosinus
sich innerhalb des Kreises befinden, können deren Werte maximal
den Wert 1 (respektive -1) erreichen. Der Tangens hingegen kann
beliebig grosse Werte annehmen und ist für den Fall, dass der Punkt
P sich ganz oben respektive ganz unten befindet nicht definiert2. Achtung: der Tangens wird immer
vom Punkt (1/0) aus senkrecht zur (beidseitig verlängerten) Geraden gemessen, auch dann, wenn
der Winkel zwischen 90° und 270° liegt.
Die Graphen der drei Funktionen sind
links abgebildet. Der Cosinus hat
prinzipiell die gleiche Form wie der
Sinus, einfach um eine Vierteldrehung
versetzt3. Der Tangens steigt zunächst
flach und dann immer steiler an, bevor
er bei einer Vierteldrehung von +∞ auf
-∞ springt.
1
2
3
Die meisten anderen Funktionen zeigen an beiden Enden (±∞) ein eher langweiliges geradliniges Verhalten.
Der Definitionsbereich des Tangens muss entsprechend diese Punkte ausschliessen.
Merksatz: Der Cosinus fängt oben an, der Sinus in der Mitte.
Trigonometrie
1/5
Jörg Mäder (01.03.2014)
Mathematische Winkelsysteme
Architekten und Ingenieure nutzen für Winkel in der Regel das Gradsystem (englisch degree,
abgekürzt: deg), das eine volle Kreisumdrehung in 360° aufteilt. Dieses System ist auch aus der
Geometrie bekannt. In der Algebra und Analysis ist zudem das Bogenmass-System (englisch
radian, abgekürzt rad) verbreitet. Dieses basiert wiederum auf dem Einheitskreis. Dieser hat nach
der Formel U =2 π r einen Umfang von 2π. Und genau dieser Wert wird einer vollen
Umdrehung zugeordnet. Ähnlich wie die Zahl e, ist dieses Winkelsystem im Alltag eher unhandlich,
erweist sich aber in verschiedenen Berechnungen4 als vorteilhaft.
Die Umrechnung zwischen diesen beiden ist recht einfach (g: Winkel in Grad, b in
180
g=b π
Bogenmass). Bei TR und Computerprogramme ist darauf zu achten, mit welchem
b=g π
Winkelsystem gearbeitet wird. Missverständnisse führen hier zu grossen Fehlern. In
180
Formeln sollte man Winkelangaben im Gradmass stets mit dem °-Zeichen versehen
(Beispiel: 45°), im Bogenmass wenn möglich als Multiplikation von π (Beispiel: 2.5π) oder mit
einem r markiert (0.56r).
In der Mathematik wird der Winkel immer im Gegenuhrzeigersinn gemessen, startend von der
rechten Hälfte der X-Achse.
Umkehrfunktionen
Alle drei trigonometrischen Funktionen haben entsprechende Umkehrfunktionen: Arcussinus
(arcsin, asin oder sin-1), Arcuscosinus (arccos, acos oder cos-1) und Arcustangens (arctan, atan oder
tan-1) . Da sin und cos nur Werte zwischen -1 und +1 liefern, sind auch nur Zahlen aus diesem
Bereich als Argumente für asin und acos zugelassen, der atan kann hingegen für alle reellen Zahlen
berechnet werden. Als Ergebnis liefern asin und atan nur Werte zwischen -90° und +90°, acos
solche zwischen 0° und 180°.
Ein TR liefert also sowohl für asin(sin (60 °)) und asin(sin (120° )) den Wert 60° zurück. Will
man aber gültige Lösungen aus einem anderen Bereich haben, muss man die Lösungen des TR
gemäss Grafik (vorherige Seite) verschieben um diese zu erhalten ( n∈ℤ, n: ... -2, -1, 0, 1, 2 ...):
sin: n⋅360 ° +α & n⋅360 ° +180 °−α cos: n⋅360 ° +α & n⋅360 °−α tan: n⋅180° +α
4
Speziell bei Differential und Integral.
Trigonometrie
2/5
Jörg Mäder (01.03.2014)
Geometrie
Vorbemerkungen zu Dreiecken
In einem Dreieck gilt bezüglich Beschriftung, dass die zu einem
Winkel gehörende Seite (α & a) gegenüber liegt. Typischerweise wir
im Uhrzeigersinn angeschrieben.
Die wichtigsten Regeln im Dreieck sind:
Winkelsumme: 180°
Fläche=
Seite⋅Höhe
2
Ist in einer Skizze kein brauchbares Dreieck sichtbar, darf man nach
Belieben Linien verlängern oder zusätzliche einzeichnen. Beispielsweise
in der Skizze links die gestrichelten, um einen rechten Winkel (rechts
unten) zu erhalten.
rechtwinkliges Dreieck
Die Skizze mit dem Einheitskreis zeigt ein rechtwinkliges Dreieck, bei dem Sinus und Cosinus je
eine Kathete bilden und der Radius die Hypotenuse. Somit gilt nach dem Satz von Pythagoras (Die
Summe der Katheten-Quadrate entspricht dem Quadrat der Hypotenuse): sin( ϕ)2 +cos (ϕ)2=1
Für ein Kreis mit Radius r≠1 gelten folgende Verallgemeinerungen:
sin(ϕ)=
Gegenkathete
Hypothenuse
cos (ϕ)=
Ankathete
Hypothenuse
tan (ϕ)=
Gegenkathete
Ankathete
Um diese Grundgesetze der Trigonometrie anwenden zu können, muss ein rechtwinkliges Dreieck
gesucht werden. Die drei Grundgesetze beinhalten einen Winkel und zwei Seiten. Sind zwei dieser
drei Werte bekannt, kann der fehlende berechnet werden. Welches der drei Gesetze zur Anwendung
kommt, kann man aus den
Skizzen rechts ablesen. Die
vierte Skizze entspricht dem
Pythagoras
Allgemeines Dreieck
Sinussatz:
sin (α) a
=
sin (β) b
Cosinussatz: c 2=a2 + b2−2 a b cos ( γ)
Diese beiden Sätze gelten im allgemeinen Dreieck5, es muss also nicht zwingend ein rechter
Winkel vorhanden sein. Somit sind auch alle Seiten und Winkel untereinander gleichwertig.
Entsprechend könnte der Sinussatz auch mit den Seiten b und c und den zugehörigen Winkeln
formuliert werden.
Der Sinussatz besteht aus zwei Winkeln und den
zugehörigen Seiten, der Cosinussatz aus einem Winkel
und allen drei Seiten (er ist eine Art Verallgemeinerung
des Satz des Pythagoras). Sind jeweils drei der vier
Grössen bekannt, kann die fehlende berechnet werden.
5
Nicht vergessen: Laut Konvention liegt die Seite a gegenüber dem Winkel α.
Trigonometrie
3/5
Jörg Mäder (01.03.2014)
Nicht mathematische Winkelsysteme
Kreise und Unterteilungen davon haben auch ausserhalb der Mathematik grosse Bedeutung. Nicht
immer werden diese aber in 360° unterteilt.
• Zeit:
Einteilung in 12 (Stunden) respektive 60 Einheiten (Minuten und Sekunden).
Im Uhrzeigersinn gemessen, oben startend.
• Geographie6
◦ Himmelsrichtung:
360° im Uhrzeigersinn, oben startend; Nord: 0°, Ost: 90°, Süd: 180° West: 270°
◦ Positionsangabe:
▪ Längengrad:
360° von West nach Ost gemessen, beim Nullmeridian (Greenwich, GB) startend
West: -180° (oder 180°W), Nullmeridian: 0°, Ost: +180° (oder 180°E, E für East)
▪ Breitengrad:
Halbkreis 180°, Von Süd nach Nord gemessen, am Äquator startend
Nordpol: +90° (oder 90°N), Äquator: 0°, Südpol: -90° (oder 90°S)
• Zählen der Umdrehungen:
Vollkreis = 1 Umdrehungen.
Richtung und Startpunkt je nach Anwendung. Häufig bei (Stell-) Motoren verwendet.
• (als Vergleich) Mathematik:
360° (Gradmass) oder 2π (Bogenmass), sehr selten 400g (Neugrad)
im Gegenuhrzeigersinn, rechts (auf der positiven Hälfte der x-Achse) startend.
6
Werte kleiner 1° werden entweder dezimal oder mit Minuten und Sekunden notiert.
15°20'30“ = 15.3416667°. Umrechnung analog zur Zeitmessung.
Trigonometrie
4/5
Jörg Mäder (01.03.2014)
Zusammengesetze Schwingungen
Jedes kontinuierliche7 periodische Signal kann als Summe von mehreren Sinusfunktionen
ausgedrückt werden. Die Überlagerung von mehreren periodischen Funktionen (Wellen) wird in der
Physik als Interferenz bezeichnet. Die blaue Kurve unten besteht aus drei Sinusschwingungen
sin( x+ π /3)+ 0.5⋅sin( 4x)+ 0.2⋅sin(6x ) , wobei die mit der tiefsten Frequenz (rot) um 60° (π/3)
verschoben ist (Phasenverschiebung, Summand in der Klammer) und die anderen beiden mit
höheren Frequenzen (Faktor in der Klammer) und kleineren Amplituden (Faktor vor der Klammer)
versehen sind.
Die Zerlegung eines periodischen Signals in seine Einzelkomponenten wird als Frequenzzerlegung
bezeichnet und wird mittels Fouriertransformation gemacht (höhere Mathematik). Der am
häufigsten eingesetzte Algorithmus ist die Fast-Fourier-Transformation (FFT).
Schwebungen
Sind die Frequenzen zweier Komponenten sehr
ähnlich, entstehen sogenannte Schwebungen.
Diese sind meist sehr störend, da sich die
beiden Signale zeitweise aufheben (Summe
nahe bei 0) oder verstärken. Dadurch fängt die
Amplitude mit einer tiefen Frequenz an zu
oszillieren.
Beispiel rechts: sin(50 x)+sin(60 x)
Hüllkurve
Oft ist man bei einem schnell schwingenden Signal nicht an den
einzelnen Schwingungen interessiert, sondern am Verhalten auf einer
etwas grösseren Zeitskala. Im Beispiel der Schwebung im lässt sich der
Form dieser Hüllkurve leicht erahnen.
7
Kontinuierlich: die Funktion weist keine Sprünge auf.
Trigonometrie
5/5
Jörg Mäder (01.03.2014)