Übung 10-I: Stichproben

!
"
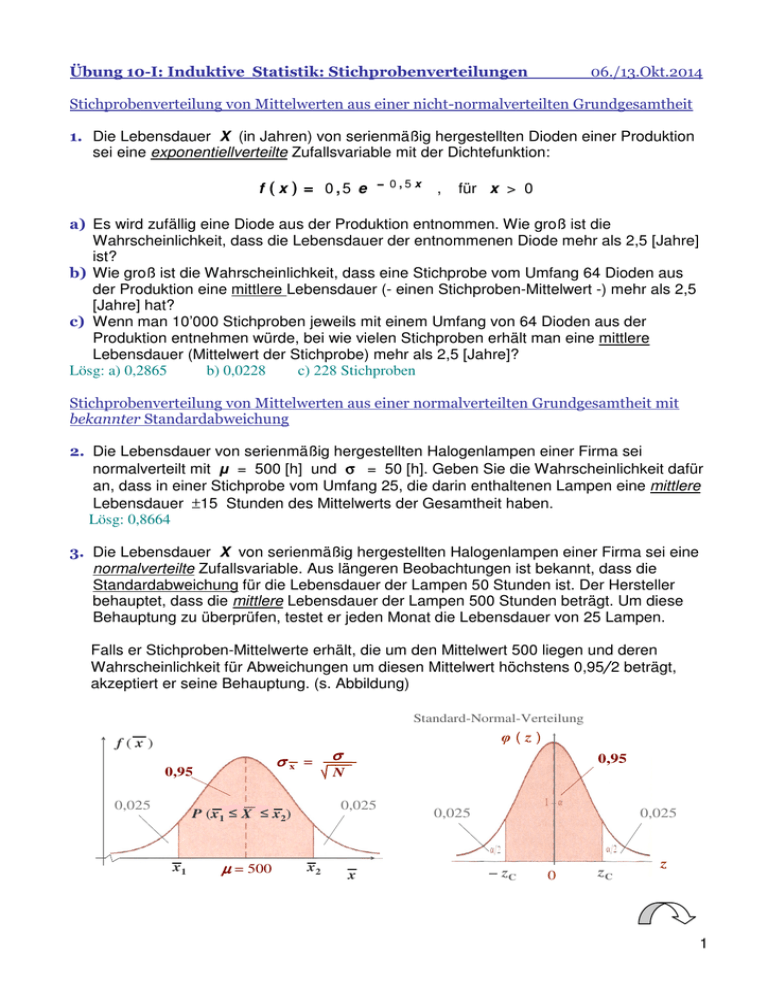
Die Lebensdauer X (in Jahren) von serienmäßig hergestellten Dioden einer Produktion
sei eine exponentiellverteilte Zufallsvariable mit der Dichtefunktion:
f (x
) = 0,5 e
− 0,5 x
,
für x > 0
Es wird zufällig eine Diode aus der Produktion entnommen. Wie groß ist die
Wahrscheinlichkeit, dass die Lebensdauer der entnommenen Diode mehr als 2,5 [Jahre]
ist?
Wie groß ist die Wahrscheinlichkeit, dass eine Stichprobe vom Umfang 64 Dioden aus
der Produktion eine mittlere Lebensdauer (- einen Stichproben-Mittelwert -) mehr als 2,5
[Jahre] hat?
Wenn man 10’000 Stichproben jeweils mit einem Umfang von 64 Dioden aus der
Produktion entnehmen würde, bei wie vielen Stichproben erhält man eine mittlere
Lebensdauer (Mittelwert der Stichprobe) mehr als 2,5 [Jahre]?
Lösg: a) 0,2865
b) 0,0228
c) 228 Stichproben
!
"
" "
Die Lebensdauer von serienmäßig hergestellten Halogenlampen einer Firma sei
normalverteilt mit
= 500 [h] und
= 50 [h]. Geben Sie die Wahrscheinlichkeit dafür
an, dass in einer Stichprobe vom Umfang 25, die darin enthaltenen Lampen eine mittlere
Lebensdauer ±15 Stunden des Mittelwerts der Gesamtheit haben.
Lösg: 0,8664
Die Lebensdauer X von serienmäßig hergestellten Halogenlampen einer Firma sei eine
normalverteilte Zufallsvariable. Aus längeren Beobachtungen ist bekannt, dass die
Standardabweichung für die Lebensdauer der Lampen 50 Stunden ist. Der Hersteller
behauptet, dass die mittlere Lebensdauer der Lampen 500 Stunden beträgt. Um diese
Behauptung zu überprüfen, testet er jeden Monat die Lebensdauer von 25 Lampen.
Falls er Stichproben-Mittelwerte erhält, die um den Mittelwert 500 liegen und deren
Wahrscheinlichkeit für Abweichungen um diesen Mittelwert höchstens 0,95 2 beträgt,
akzeptiert er seine Behauptung. (s. Abbildung)
Standard-Normal-Verteilung
(z)
f(x)
σx =
0,95
0,025
P (x1
x1
X
µ = 500
σ
0,95
N
0,025
x2)
x2
x
0,025
0,025
– zC
0
zC
z
1
Bei welchem der folgenden Fälle kann er seine Behauptung annehmen und bei welchem
muss er sie verwerfen?
wenn er bei einer Stichprobe den Mittelwert x = 516 [h] erhält?
wenn er bei einer Stichprobe den Mittelwert x = 475 [h] erhält?
#
"
+
!
$
"
"
%& "
'
()
"
*
"
"
,
Lösg:
a) Der Hersteller kann annehmen, dass seine Behauptung richtig ist.
b) Der Hersteller muss seine Behauptung verwerfen, die mittlere Lebensdauer ist geringer als 500 [h].
!
"
" "
! Die Lebensdauer X von serienmäßig hergestellten Halogenlampen einer Firma sei eine
normalverteilte Zufallsvariable. Der Hersteller behauptet, dass die mittlere Lebensdauer
der Lampen 500 Stunden beträgt. Um diese Behauptung zu überprüfen, testet er jeden
Monat die Lebensdauer von 25 Lampen.
Falls er Stichproben-Mittelwerte erhält, die um den Mittelwert 500 liegen und deren
Wahrscheinlichkeit für Abweichungen um diesen Mittelwert höchstens 0,9 2 beträgt,
akzeptiert er seine Behauptung. (s. Abb.)
Studentsche-t-Verteilung
fν (t)
0,9
–
0,05
0,05
– tC
0
tC
t
Bei welchem der folgenden Fälle kann er seine Behauptung annehmen und bei welchem
muss er sie verwerfen?
wenn er bei einer Stichprobe den Mittelwert x = 485 [h] und die Standardabweichung
s = 45 [h] erhält?
wenn er bei einer Stichprobe den Mittelwert x = 480 [h] und die Standardabweichung
s = 50 [h] erhält?
Lösg:
a) Der Hersteller kann annehmen, dass die Behauptung richtig ist.
b) Der Hersteller muss seine Behauptung verwerfen, die mittlere Lebensdauer ist geringer 500 [h]
2
3
4
5