Übungen zur Vorlesung „Technische Informatik I“, SS 2001 Hauck
Werbung
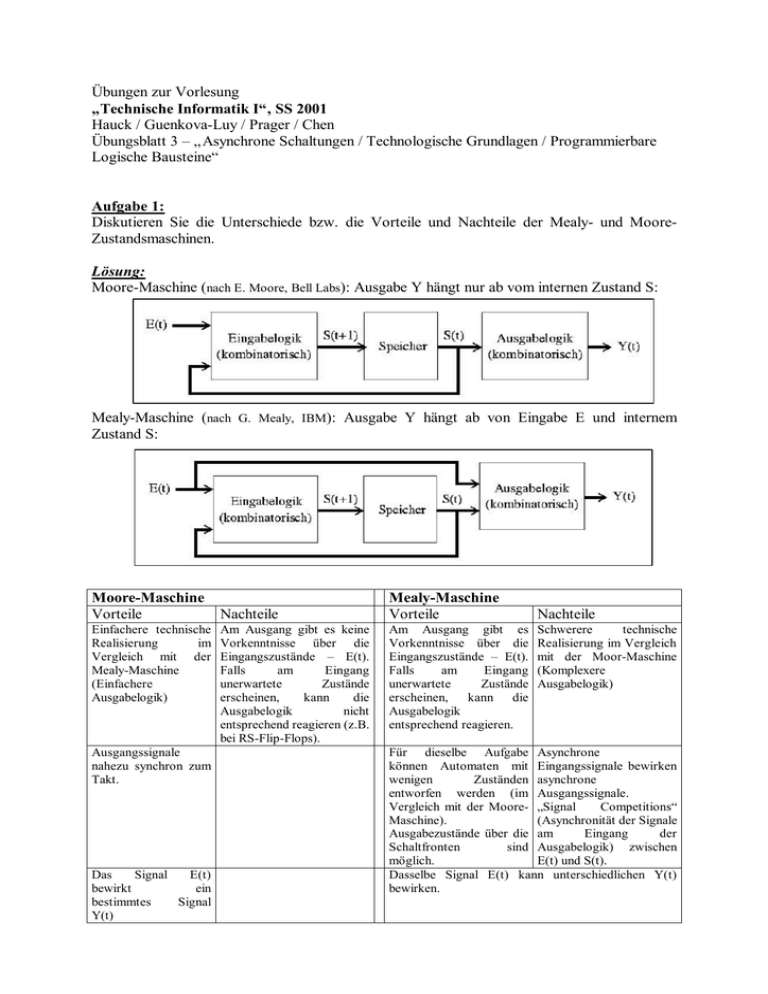
Übungen zur Vorlesung „Technische Informatik I“, SS 2001 Hauck / Guenkova-Luy / Prager / Chen Übungsblatt 3 – „Asynchrone Schaltungen / Technologische Grundlagen / Programmierbare Logische Bausteine“ Aufgabe 1: Diskutieren Sie die Unterschiede bzw. die Vorteile und Nachteile der Mealy- und MooreZustandsmaschinen. Lösung: Moore-Maschine (nach E. Moore, Bell Labs): Ausgabe Y hängt nur ab vom internen Zustand S: Mealy-Maschine (nach G. Mealy, IBM): Ausgabe Y hängt ab von Eingabe E und internem Zustand S: Moore-Maschine Vorteile Einfachere technische Realisierung im Vergleich mit der Mealy-Maschine (Einfachere Ausgabelogik) Ausgangssignale nahezu synchron zum Takt. Das Signal E(t) bewirkt ein bestimmtes Signal Y(t) Nachteile Am Ausgang gibt es keine Vorkenntnisse über die Eingangszustände – E(t). Falls am Eingang unerwartete Zustände erscheinen, kann die Ausgabelogik nicht entsprechend reagieren (z.B. bei RS-Flip-Flops). Mealy-Maschine Vorteile Am Ausgang gibt es Vorkenntnisse über die Eingangszustände – E(t). Falls am Eingang unerwartete Zustände erscheinen, kann die Ausgabelogik entsprechend reagieren. Nachteile Schwerere technische Realisierung im Vergleich mit der Moor-Maschine (Komplexere Ausgabelogik) Für dieselbe Aufgabe Asynchrone können Automaten mit Eingangssignale bewirken wenigen Zuständen asynchrone entworfen werden (im Ausgangssignale. Vergleich mit der Moore- „Signal Competitions“ Maschine). (Asynchronität der Signale Ausgabezustände über die am Eingang der Schaltfronten sind Ausgabelogik) zwischen möglich. E(t) und S(t). Dasselbe Signal E(t) kann unterschiedlichen Y(t) bewirken. Aufgabe 2: Gegeben ist die folgende Schaltung: a. b. c. d. Ist die Schaltung als synchron oder asynchron zu klassifizieren? Zeichnen Sie das Zeitdiagramm der Schaltung Stellen Sie das Übergangsdiagramm und die Übergangstabelle der Schaltung dar Was für Funktionen hat diese Schaltung? Lösung: a. Die Schaltung ist ein asynchrones Schalwerk, da die Takteingänge des zweiten und des dritten Flip-Flops nicht mit dem Systemtakt C beschaltet sind. b. Zeitdiagramm c. Übergänge Übergangsdiagramm Übergangstabelle q2(alt) q1(alt) 0 0 0 0 0 1 0 1 1 0 1 0 1 1 1 1 q0(alt) 0 1 0 1 0 1 0 1 q2(neu)=d2(alt) 0 0 0 1 1 1 1 0 q1(neu) =d1(alt) 0 1 1 0 0 1 1 0 q0(neu) =d0(alt) 1 0 1 0 1 0 1 0 d. Die Schaltung kann als Mod-8-Zähler oder als Frequenzteiler verwendet werden. Aufgabe 3: Welche Funktionalität hat die folgende CMOS-Schaltung (Begründung !) ? Die einzelnen Transistoren funktionieren folgendermaßen: n-MOS Gate-Source Spannung +5V 0V leitet sperrt Lösung: Das ist ein NOR Gatter. p-MOS Gate-Source Spannung -5V 0V leitet sperrt Für die Pegel von A und B ergeben sich folgende Konstellationen: A=0 (mit Masse verbunden): Q1 leitend, Q3 sperrt A=1 (mit VDD/Versorgungsspannung 5-15V verbunden): Q1 sperrt, Q3 leitend B=0: Q2 leitend, Q4 sperrt B=1: Q2 sperrt, Q4 leitend Wenn Q1 und Q2 leitend sind, sind Q3 und Q4 gesperrt, d.h. Y liegt an VDD, Y=1. Die Verbindung zu Masse ist durch die gesperrten Transistoren nahezu abgetrennt. Wenn Q1 oder Q2 gesperrt sind entweder Q3 oder Q4 (oder beide) leitend, wodurch Y an Masse gebunden ist, Y=0. Die Verbindung zu VDD ist dagegen durch wenigstens einen gesperrten Transistor Q1 oder Q2 getrennt. Die Transistoren verknüpfen also Y immer mit VDD oder Masse und sperren gleichzeitig zur jeweils anderen Seite, um einen Kurzschluss zu vermeiden. Aus der Beschaltung ergibt sich die Funktionalität eines NOR-Gatters. Aufgabe 4: Realisieren Sie die Funktionen A<B – A kleiner B, A=B – A gleich B, A>B – A größer B und Α<> B – A ungleich B (A und B sind 2-Bit Binärzahlen) mit den folgend gezeigten PROM, PAL und PLA. Welche Realisierung ist die günstigste? Lösung: a1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 a0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 b1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 b0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 X⇒ a<b 0 1 1 1 0 0 1 1 0 0 0 1 0 0 0 0 Y⇒ a=b 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 Z⇒ a>b 0 0 0 0 1 0 0 0 1 1 0 0 1 1 1 0 Minimierte Funktionen: X = a1⋅b1 + a 0 ⋅a1⋅b0 + a 0 ⋅b0 ⋅b1 Y = a0 ⋅a1⋅b0 ⋅b1 + a 0 ⋅a1 ⋅b0 ⋅b1 + a0 ⋅a1 ⋅b0 ⋅b1 + a 0 ⋅a1 ⋅b0 ⋅b1 Z = a1⋅b1 + a 0 ⋅b0 ⋅b1 + a0 ⋅a1 ⋅b0 W = a 0 ⋅b0 + a0 ⋅b0 + a1⋅b1 + a1 ⋅b1 a. PROM – Nichtminimierte Funktion, kleinsten Programmieraufwand a1 a0 b1 b0 W Z Y X W⇒ a<>b 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0 b. PAL – Teilweise-minimierte Funktion, mittleren Programmieraufwand a1 a0 b1 b0 W X Y Z c. PLA – Minimierte Funktion, größten Programmieraufwand a1 a0 b1 b0 W X Y Z Aufgabe 5: Gegeben ist ein programmierbarer Logik-Baustein vom Typ GAL20RA10, dessen LogikMakrozelle gemäß folgendem Bild aufgebaut ist Die zusätzlichen Flip-Flop Eingänge haben hier folgende Bedeutung: AR – Asynchronous Reset AP – Asynchronous Preset PL – Parallel Load (Daten werden von PD eingelesen) PD – Parallel Data (Dateneingang für paralleles Laden) Hinweis: Die Beschreibung des Bausteins GAL20RA10 sehen Sie als Anlage zu der Übung. a. Erklären Sie die Bedeutung der einzelnen Komponenten. Wozu dient das XORGatter(XOR(n) ist für jede Makrozelle mit 0 oder 1 programmierbar)? Welchen Sinn hat der Multiplexer am Ausgang des Flip-Flops? b. Einwerfen Sie ein JK-Flip-Flop, benutzen Sie dabei das D-Flip-Flop des GAL20RA10. Wie müssen die Komponenten des Bausteins beschaltet werden? Lösung: a. Multiplexer 0 – Flip- Flop Ausgang 1 – Direkter Ausgang der UND-Matrix Ausgang aktivieren Takt 00 und 11 Steuereingang des Multiplexers 01 Asynchronous Preset 10 Asynchronous Reset UNDMatrix Eingänge (wie PAL) Eingang (Programmiermodus) / Ausgang des Flip-Flops oder der UND-Matrix(Betriebmodus) Normaler und negierter Ausgang des Flip-Flops XOR 0 – normaler Eingang des Flip-Flops 1 – negierter Eingang des Flip-Flops b. Die Abbildungen zeigen nur Ausschnitte des Bausteins GAL20RA10 und nur die Komponenten, die für die jeweilige Lösung benutzt worden sind. Die grau gekennzeichneten Komponenten sind Zusatzkomponenten. Systematische Lösung: J K Q(t1) Q(t2) D 0 0 0 Q(t1) 0 0 0 1 Q(t1) 1 1 0 0 0 0 1 1 0 0 1 0 0 1 1 1 0 1 1 1 1 1 0 Q(t1) 1 1 1 1 Q(t1) 0 0 Nach Minimierung: J ⋅Q + K ⋅Q Alternative Lösung (unsystematisch und asynchron):