LU 11 Theorie Kongruenz und Trapez

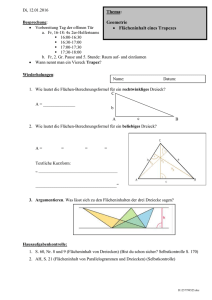
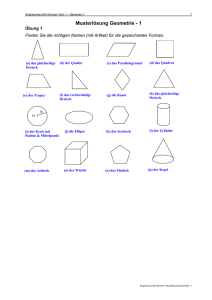
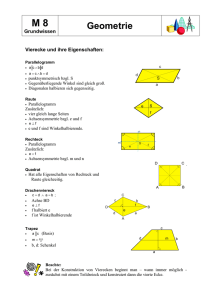
MB2 LU 11 Dreieckskonstruktionen Kongruenzsätze
Siehe auch MB1 LU 12
Zur Erinnerung:
Dreiecke werden so beschriftet:
Die grösste Seite eines Dreiecks
liegt gegenüber dem grössten Winkel!
MB2 LU 11 Dreieckskonstruktionen Kongruenzsätze
Siehe auch MB1 LU 12
Zur Erinnerung:
C
γ
Dreiecke werden so beschriftet:
b
Die grösste Seite eines Dreiecks
liegt gegenüber dem grössten Winkel!
A
α
a
C
β
B
in allen drei Seiten übereinstimmen.
in zwei Seiten und dem eingeschlossenen
Winkel übereinstimmen.
in einer Seite und den beiden anliegenden
Winkeln übereinstimmen.
in zwei Seiten und dem Winkel welcher
gegenüber der grösseren Seite liegt,
übereinstimmen.
MB2 LU 11 Entwicklung von 2 bis 8
5.
4.
3.
2.
1.
Suche Flächen, die zu den 5 nummerierten kongruent, genau deckungsgleich sind.
Notiere auf diese Flächen dieselbe Nummer.
Notiere zu jeder Nummer wie man die Fläche nennt.
1.
2.
3.
4.
5.
Stumpfwinkliges Dreieck
.
.
.
.
Flächen nennt man ähnlich, wenn sie in allen Winkeln übereinstimmen.
Flächen nennt man kongruent (deckungsgleich) wenn sie in allen Winkeln und in
allen Längen übereinstimmen.
MB2 LU 11 Entwicklung von 2 bis 8 Lös
1.
2.
3.
4.
5.
1.
5.
2.
3.
2.
1.
4.
3.
2.
1.
Suche Flächen, die zu den 5 nummerierten kongruent, genau deckungsgleich sind.
Notiere auf diese Flächen dieselbe Nummer.
Notiere zu jeder Nummer wie man die Fläche nennt.
1.
2.
3.
4.
5.
Stumpfwinkliges Dreieck
Spitzwinkliges Dreieck
Trapez
Trapez
Trapez
Flächen nennt man ähnlich, wenn sie in allen Winkeln übereinstimmen.
Flächen nennt man Kongruent (Deckungsgleich) wenn sie in allen Winkeln und in
allen Längen übereinstimmen.
MB2 LU 11 Trapezflächenformel
Figur
Formel
m
m
A=m∙h
Beschreibung
Die beiden Ecken unten werden senkrecht zur
Grundseite bis zur Mitte der Schenkel abgeschnitten
und oben angehängt. Es entsteht ein flächengleiches
Rechteck. Man Berechnet zuerst die Länge der
Mittelparallelen m. (Durchschnitt von g1 und g2 und
Berechnet die Rechteckfläche m ∙ h.
MB2 LU 11 Trapezflächenformel
Figur
Formel
Beschreibung
Doppeltes Trapez ist ein Parallelogramm mit
Grundseite (g1 + g2) und Höhe h. Man berechnet
zuerst diese Parallelogrammfläche und halbiert sie.
Der obere Teil des Trapezes wird entlang der
Mittelparallelen abgeschnitten und auf einer Seite
angehängt Es entsteht ein Parallelogramm mit
Grundseite (g1 + g2) und Höhe
diese Parallelogramfläche
h
. Man berechnet
2
Das Trapez wird in ein Parallelogramm und ein
Dreieck zerlegt. Man berechnet die
Parallelogrammfläche und die Dreieckfläche und
bildet die Summe.
g1 ̶– g2 ̶
Das Trapez wird in zwei Dreiecke zerlegt. Man
berechnet die beiden Dreieckflächen und bildet die
Summe.
m
m
A=m∙h
Die beiden Ecken unten werden senkrecht zur
Grundseite bis zur Mitte der Schenkel abgeschnitten
und oben angehängt. Es entsteht ein flächengleiches
Rechteck. Man Berechnet zuerst die Länge der
Mittelparallelen m. (Durchschnitt von g1 und g2 und
Berechnet die Rechteckfläche m ∙ h.
MB2 LU 11
Kleine Formelsammlung -
die musst du gut kennen, und mit Zeichnungen und Text erklären können !!!!
Flächenberechnungen
Rechteck
A = a ∙ b = Länge mal Breite
b
a
----------------------------------------------------------------------------------------------------------------------------------------------------
Parallelogramm
A = a ∙ h = Grundseite mal Höhe
b
h
a
----------------------------------------------------------------------------------------------------------------------------------------------------
Dreieck
A
A = a ∙ ha : 2
ha
B
= Grundseite mal Höhe durch 2
Dreieck ist ein halbes Rechteck!
C
a
----------------------------------------------------------------------------------------------------------------------------------------------------
Trapez
A=
a ⋅h c ⋅h
+
2
2
m=
A=
(a + c) ⋅ h
= (a + c) ⋅ h : 2
2
(a + c)
2
A = m⋅h
----------------------------------------------------------------------------------------------------------------------------------------------------
Drachen
A=e∙f:2
e
f
Zuerst Rechteckfläche e mal f,
dann halbieren!