3.3 Durchlaufen von Graphen

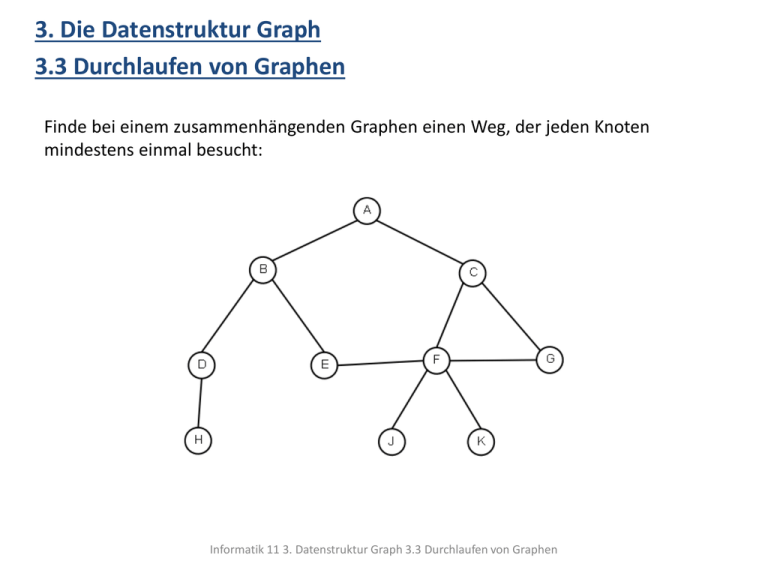
3. Die Datenstruktur Graph
3.3 Durchlaufen von Graphen
Finde bei einem zusammenhängenden Graphen einen Weg, der jeden Knoten
mindestens einmal besucht:
Informatik 11 3. Datenstruktur Graph 3.3 Durchlaufen von Graphen
3.3 Durchlaufen von Graphen
Ein möglicher Algorithmus ist die Tiefensuche :
Wähle einen Startknoten
Besuche einen der möglichen Nachbarn (bei mehreren Nachbarn z.B.
alphabetisch oder numerisch auswählen) und markiere ihn als besucht.
Besuche von diesem Knoten wieder einen Nachbarn, der noch nicht besucht
wurde.
Sind bei einem Knoten alle Nachbarn markiert oder führt kein Weg weiter, so
ist dieser fertig abgearbeitet. Gehe zu dem Nachbarknoten zurück, von dem
aus dieser Knoten besucht wurde.
Informatik 11 3. Datenstruktur Graph 3.3 Durchlaufen von Graphen
3.3 Durchlaufen von Graphen
Mögliches Ergebnis der Tiefensuche:
A  B  D H ;
H fertig; D fertig
B  E  F C  G;
G fertig; C fertig
FJ;
J fertig
FK;
K fertig
F fertig
E fertig
B fertig
A fertig
Informatik 11 3. Datenstruktur Graph 3.3 Durchlaufen von Graphen
3.3 Durchlaufen von Graphen
Algorithmus zur Tiefensuche:
Klasse GRAPH_MATRIX
void tiefensuche(String startknoten)
Wenn der Startknoten existiert (die Knotennummer ist ungleich -1), werden in dem Feld
besucht vom typ boolean alle Werte auf false gesetzt.
Anschließend ruft man die Methode besuchen auf, welche die Tiefensuche durchführt.
Klasse GRAPH_MATRIX
void besuchen(int knotennummer)
Der aktive Knoten wird durch den entsprechenden Eintrag im Feld besucht auf besucht
gesetzt und in der Konsole ausgegeben.
In der Matrix sucht man in der Zeile des aktiven Knotens nach möglichen
Nachbarknoten, d.h. vom aktiven Knoten bis zum Ende nach Einträgen ungleich -1.
Gibt es in dieser Zeile eine Kante, deren Zielknoten außerdem noch nicht besucht
wurde, geht man in die Tiefe und besucht durch rekursiven Aufruf der Methode
besuchen den Abzweigknoten.
Ist die Zeile der Matrix vollständig durchlaufen, so ist der Knoten auch fertig
abgearbeitet. Dies wird in der Konsole ausgegeben.
Informatik 11 3. Datenstruktur Graph 3.3 Durchlaufen von Graphen