ATOMPHYSIK

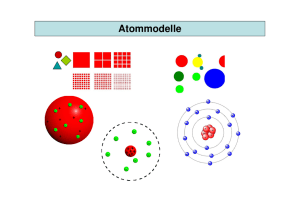
ATOMPHYSIK
Gábor Talián
Univ. Pécs, Institut für Biophysik
15-22. September 2016
PRÜFUNGSTHEMA
Die Temperaturstrahlung.
Das plancksche Wirkungsquantum.
Der photoelektrische Effekt.
Experimentelle Beobachtungen und Erklärung des
Phänomens. Die Einstein-Gleichung.
Lehrbuch: 106-113 S.
Ende XIX-en Jahrhunderts
Aufbau von Physik grundsätzlich beendet.
Erkannte Zusammenhänge und Konstanten
müssen nur genauer gemacht werden:
Im XX-en Jahrhundert wird es die Physik der
fünften Stelle nach dem Komma sein.
Das klassische physikalische Modell
Physik beruht sich auf den Gesetzen der herkömmlichen
Mechanik, den Maxwell-Gleichungen in Elektromagnetischen
Erscheinungen und der statistischen Verteilung von Energie in
thermodynamischen Systemen.
Die Bewegungsparameter und die Position der Körper – von den
größten (wie Sternen und Planeten) bis ab den kleinsten (?) – ist
theoretisch beliebig genau in jedem Moment zu berechnen.
Die Eigenschaften eines Systems sind in jedem zustand eindeutig
bestimmt und können in den nachkommenden Zuständen
ebenso erkannt und vorhergesagt werden.
Einige winzige, unangenehme Wolken
auf dem klaren Himmel der Physik
•
•
•
•
•
•
Radioaktivität
Schwarzkörperstrahlung
Photoelektrischer Effekt
Linienspektrum von Elementen (H)
Spezifische Wärme der Gase
Konstanz der Lichtgeschwindichkeit
Sie waren aber erwartet bald erklärt und in das klassische
Modell gefügt zu werden.
Die Grundstruktur der Materie:
Gibt es Atome?
• Leukipp, Demokrit
atomos (ατομος) – unteilbar
• Dalton (1803)
–
–
–
–
Stoffe bestehen aus unteilbaren Atomen
Atome können nicht geschöpft oder zerstört werden
Die Atome eines Elementes sind gleich
Die Atome verschiedener Elemente unterscheiden
sich nur in Größe und Masse
– in Verbindungen mischen sich die Atome nach
konstanten Proportionen (wie ganze Zahlen)
Massenerhaltung
Biliardkugel-Modell
• Mendelejev - periodisches System
• J.J.Thomson
(1897)
– Entdeckung des Elektrons, Einheit von negativer elektrischer Ladung
– Es entsteht aus jedem Element (Metall im Kathodenstrahlrohr)
– Seine Masse ist ~1800-fach weniger als die des leichtesten Elements (H)
– Das Atom kann nicht unteilbar bzw. der kleinste Baustein
des Stoffes sein!
„Rosinenkuchenmodell“ (1904)
• Ludwig Boltzmann
Er beging Selbstmord in 1906 (!), weil seine Kollegen ihm nicht abnehmen
wollten, dass es Atome wirklich gibt.
(heute: Einzelne Atome können mit Rastertunnelmikroskop untersucht
-„gesehen“ - werden.)
PROBLEM I. :
SCHWARZKÖRPERSTRAHLUNG
Problemstellung:
Körper können EM Strahlung
aufnehmen
und
abgeben.
Wie
kann
das
Ausstrahlungsspektrum des schwarzen Körpers erklärt
werden?
Schwarzkörperstrahlung
∙ 5,67 ∙ 10
Stefan-Bolzmann Konstante
Wilhelm Wien,
1864-1928
Ludwig Boltzmann,
1844-1906
Jozef Stefan,
1835-1893
Schwarzkörperstrahlung
„Die große Tragödie der Wissenschaft - die Erledigung einer
wunderschönen Hypothese durch eine häßliche Tatsache“
Thomas Huxley
! 6,626 ∙ 10
#
$%
Max Planck,
1858-1947
der photoelektrische Effekt
U
Albert Einstein,
1879-1955
PRÜFUNGSTHEMA
Der Rutherford-Versuch.
Das rutherfordsche Atommodell.
Die bohrschen Postulate. Das bohrsche Atommodell.
Das Teilchen-Welle Modell von de Broglie.
Der Franck-Hertz Versuch.
Lehrbuch: 106-113 S.
PROBLEM II. – LINIENSPEKTRUM VOM
WASSERSTOFF
Problemstellung:
Das
Absorptionsoder
Emissionsspektrum des Wasserstoffs besteht aus
diskreten Linien mit bestimmten Positionen bezüglich
des kontinuierlichem weißem Lichtspektrum. Es
bedeutet, dass der Wasserstoff kann Photonen nur mit
gewissen Wellenlängen/Energien aufnehmen oder
aussenden. Warum ist es so?
121,57 n m
ultraviolett
656,3 n m
102,57 n m
1875 n m
486,1 n m
97,25 n m
4050 n m
1282 n m
434 n m
2630 n m
2170 n m
1460 n m
820 n m
1094 n m
1005 n m
955 n m
410,2 n m
397 n m
388,9 n m
365 n m
91,1 n m
94,97 n m
93,78 n m
93,07 n m
92,62 n m
Das Spektrum vom Wasserstoff
sichtbar
Johann Balmer,
1825-1898
Johannes Rydberg,
1854-1919
infrarot
Wellenlänge (nm)
der Versuch von Rutherford
Ernest Rutherford,
1871-1937
„Es war so ziemlich das unglaublichste Ereignis, das mir je in meinem Leben widerfahren ist. Es
war so unglaublich, wie wenn man eine 15-Zoll-Granate auf ein Stück Seidenpapier abgefeuert
hatte, und diese wäre zurückgeprallt und hätte den Schützen getroffen“
das Planetenmodell
im Wasserstoffatom das Elektron umkreist den Atomkern
Zentripetalkraft = elektrische Kraft
(bei anderen Elementen: Wechselwirkung zwischen den Elektronen
Dreikörperproblem, usw. )
./
)
∙
&'( * ∙ + ∙ ,- 0
r
v
m F
&)1
2 ∙ 3/
0
4
. / 2 ∙ 3/
∙
* ∙ + ∙ ,- 0/
0
Klassische Physik kann die
Stabilität des Atoms nicht erklären
bohrsche Postulate
Postulat: ein Grundsatz bezeichnet für eine Theorie
oder ein formales System, der keine neuen Terme
einführt, aber nicht aus den gegebenen Definitionen
abgeleitet werden kann. Ein Postulat gilt als Axiom,
wenn sich aus ihm andere Theorien des Systems oder
der Alltagserfahrung herleiten lassen, deren Geltung
bereits bekannt ist oder beschlossen wurde.
Niels Bohr,
1885-1962
1. Elektronen bewegen sich um den Atomkern auf Kreisbahnen nach
den Gesetzen der klassischen Physik. Die Energie eines Elektrons im
Atom kann nur diskrete Werte (En) annehmen.
2. Jede Energieabgabe oder -aufnahme des Elektrons kann nur durch
Übergänge zwischen den stabilen Bahnen in Quanten erfolgen, die der
Differenz von zwei erlaubten Bahnenenergien entsprechen.
! ∙ 5 67 − 69
3. Nur wenige stabile Atombahnen des Elektrons um den Atomkern
existieren, wo es keine Energie verliert. Die Bahnen müssen die
folgende Quantenbedingung erfüllen:
: ∙;∙< =∙!
2>
Die Gesamtenergie der Bahn ist die Summe der potentiellen und der
kinetischen Energie. Elektronen in nicht erlaubten Positionen müssen
sich sofort auf die energetisch nächst niedrige stabile Bahn begeben,
und die Überschußenergie wird als EM Welle abgestrahlt.
Nur ganz bestimmte Drehimpulse sind erlaubt:
?: ∙ ; ∙ < = ∙ @
L
m
•
v
r
Teilchen als Welle
A
!
B
Louis de Broglie,
1892-1987
Kann das man auf alle Teilchen anwenden?
Ein Elektron mit 100V Beschleunigung
(v = 5.9*106 m/s)
!
6.626 ∙ 10# $ ∙ %
A
1.2 ∙ 10FK 0.12=
∙;
9.11 ∙ 10#F GH ∙ 5.9 ∙ 10I /%
Ein geworfener Baseball
(v = 40 m/s, m = 0.15 kg)
A 1.1 ∙ 10# (Atomkern: 10-14 m)
ELEKTRON: STOFF oder WELLE?
Experiment: Davisson, Germer
1926, Nobelpreis 1937
A
L
m
•
v
r
Kreislauf:
!
B
Die rydbergsche Konstante
Der Franck-Hertz Versuch (1913)
James Franck,
1882-1964
Gustav Hertz,
1887-1975
PRÜFUNGSTHEMA
Das quantenmechanische Atommodell,
Wellenfunktion.
Quantenzahlen
Der Stern-Gerlach und Eintein-de Haas Versuch.
Die heisenbergsche Unschärferelation.
Lehrbuch: 6-18 S.
PROBLEM III. – DIE WELLENNATUR DES
ELEKTRONS
Problemstellung: Wie kann etwas sowohl ein Teilchen
als auch eine Welle sein? Was ist die „wellende”
physikalische Größe in dem Elektron?
Erwin Schrödinger,
1887-1961
de-Broglie-Wellenlänge
λ=
h
=
p
h
2m E
Quantenzahlen
l ist die Nebenquantenzahl
: P ∙ P M 1 ∙
!
2∙>
m (ml) ist die magnetische Quantenzahl
: ∙
!
2∙>
Z-komponent des Drehimpulses
in einem magnetischen Feld
Spin: Eigendrehimpuls
L % ∙ % M 1 ∙
!
2∙>
s ist die Spinquantenzahl N 4//
!
L ∙
2∙>
Z-komponent des Drehimpulses in einem magnetischen Feld
ms ist die magnetische Spinquantenzahl
2N ∓4//
Stern - Gerlach Versuch
Otto Stern,
1888-1969
Walter Gerlach,
1889-1979
Einstein - de Haas Versuch
Wander Johannes de Haas,
1878-1960)
Elektronenbahnen
heisenbergsche Unschärferelation
∆p · ∆x ≥ h/4π = ħ/2
Werner Heisenberg,
1901-1976
Impuls
∆ x ∆px ≥
Ort
h
2
Plancksche Konstante
∆ y ∆p y ≥
h
2
∆z ∆pz ≥
h
2
∆ t ∆E ≥
h
2
Zwei komplementäre Zustände (hier: Impuls und Ort) lassen sich nie mit beliebiger
Genauigkeit messen
Zentrale Unterschiede von klassicher
und quantenmechanischer Sicht
Klassische Theorien
Quantenmechanik
(Newtonsche Mechanik, Maxwell Elektrodynamik)
•Deterministisch
aus maximaler Beobachtung eindeutig
auf Zukunft und Vergangenheit schliessen
•Indeterministisch
nur wirklichscheinlichkeitsaussagen
•Teilchen:
Orts&Impuls&Zeit Punkte
•Teilchen:
Wellenfunktion
•Realität lokal
•Realität nichtlokal
d.h. räumlich entfernte Teilchen sind nur über
Kräfte verknüpft, Lichtgeschwindigkeit
•Kontinuierlich:
Energie und Drehimpuls kann
jeden Wert annehmen
auch weitentferne Teilchen sind verschränkt
(Überlichtgeschwindigkeit)
•Gequantelt:
Energie und Drehimpuls haben nur diskrete Werte
PHYSIKALISCHE KONSTANTEN
Symbol und
Formel
Zahlwert
Größenordnung
und Maßeinheit
Bemerkung
Symbol und
Formel
Lichtgeschwindigkeit in Vakuum
c0, c
2,997 924 58
108 m·s–1
Zahlwert
Größenordnung
und Maßeinheit
Konstante von Avogadro
wirklich
fundamental
NA
6,022 141
99(47)
1023
mol–1
Gravitationskonstante
G
6,673
10–11 m3·kg–1·s–2
h
4,1356
10–34 J·s
10–15
eV·s
F = e·NA
wirklich
fundamental
Elementarladung
e
1,602 176 462
10–19 C
10–31 kg
me
0,510 998 902
MeV
Nicht wirklich
fundamental;
kann errechnet
werden in Prinzip
8,314 472(15)
J·mol–1·K–1
k = R/NA
1,380 6503
8,617269
10–23 J·K–1
10–5
eV·K–1
mp
10–27 kg
1,007 276 466
u
938,271 998(38)
MeV
Nicht wirklich
fundamental;
kann errechnet
werden in Prinzip
Nicht wirklich
fundamental
mehr
wirklich
fundamental
Magnetische Permeabilität in Vakuum
µ0 = 1/∑0c2
12,566 370 614
10–7 V·s·A–1m–1
Nicht wirklich
fundamental
Elektrische Susceptibilität in Vakuum
Masse des Protons in Ruhe
1,672 621 58
Nicht wirklich
fundamental
mehr
Boltzmannsche Konstante
Masse des Elektrons in Ruhe
9,109 381 88
96 485,3415(39)
C·mol–1
Universale Gaskonstante
R
wirklich
fundamental
?
vielleicht nicht
Nicht wirklich
fundamental
mehr
Faradaysche Konstante
wirklich
fundamental
Plancksche Konstante
6,626 068 76
Bemerkung
∑0 = 1/µ0c2
8,854 187 817
10–12 A·s·V–1m–1
Nicht wirklich
fundamental
DANKE FÜR IHRE AUFMERKSAMKEIT
Ψ = Wellenfunktion
•
•
•
•
•
•
•
•
Die sich ausbreitende physikalische Grösse in Materienwellen, die alle messbaren Informationen über das
Teilchen enthält
Das Elektron wird durch die Wellenfunktion repräsentiert (Ort, Zeit), wobei ψ* ψ (= ψ2) die
Wahrscheinlichkeitsdichte für das Auffinden des Teilchens am gegebenen Ort und Zeitpunkt bedeutet.
ψ2 (Aufenthaltswahrscheinlichkeitsdichte) über den ganzen Raum summiert ist 1, weil die Wahrscheinlichkeit
für das Auffinden eines existierenden Teilchens 1 sein muss.
Ψ ist eine stetige Funktion.
Die Wellenfunktion wird in der Schrödingergleichung zur Berechnungen von Energie oder des
Wahrscheinlichsten Werts einer Variablen benutzt.
Ψ ist für ein freies Teilchen eine Sinuswelle, mit einem exakt bestimmten Impuls und einem unbestimmten Ort
(siehe später).
Die Wellenfunktion beschreibt das gebundene Elektron in drei Dimensionen, somit ist sie für den Wasserstoff
Kugelsymmetrisch.
Mit Hilfe der Wellenfunktion spielt die Schrödingergleichung die Rolle der Newtonschen Gesetze von
klassischer Mechanik in atomaren und subatomaren Systemen. Sie macht Vorhersagungen über das Verhalten
eines dynamischen Systems und die Wahrscheinlichkeit von möglichen Ereignissen und Ausgängen. Kein
einzelner Ausgang ist strikt festgelegt, für eine grosse Anzahl an Ereignissen jedoch sagt die
Schrödingergleichung die präzise Verteilung der Ergebnisse voraus.
Wichtigere Quellen
http://www.grund-wissen.de/physik/atomphysik/atommodelle.html
http://www.tf.uni-kiel.de/matwis/amat/mw1_ge/index.html