BEISPIEL ZUR NORMALVERTEILUNG - gym

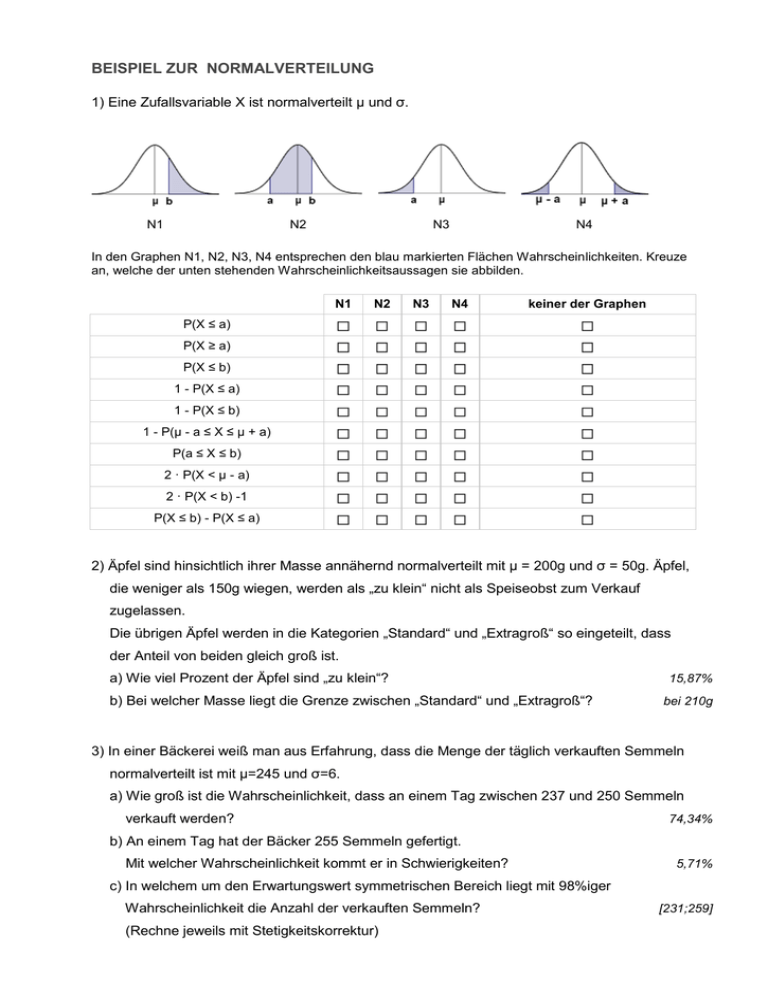
BEISPIEL ZUR NORMALVERTEILUNG
1) Eine Zufallsvariable X ist normalverteilt μ und σ.
N1
N2
N3
N4
In den Graphen N1, N2, N3, N4 entsprechen den blau markierten Flächen Wahrscheinlichkeiten. Kreuze
an, welche der unten stehenden Wahrscheinlichkeitsaussagen sie abbilden.
N1
N2
N3
N4
keiner der Graphen
P(X ≤ a)
P(X ≥ a)
P(X ≤ b)
1 - P(X ≤ a)
1 - P(X ≤ b)
1 - P(μ - a ≤ X ≤ μ + a)
P(a ≤ X ≤ b)
2 · P(X < μ - a)
2 · P(X < b) -1
P(X ≤ b) - P(X ≤ a)
2) Äpfel sind hinsichtlich ihrer Masse annähernd normalverteilt mit μ = 200g und σ = 50g. Äpfel,
die weniger als 150g wiegen, werden als „zu klein“ nicht als Speiseobst zum Verkauf
zugelassen.
Die übrigen Äpfel werden in die Kategorien „Standard“ und „Extragroß“ so eingeteilt, dass
der Anteil von beiden gleich groß ist.
a) Wie viel Prozent der Äpfel sind „zu klein“?
b) Bei welcher Masse liegt die Grenze zwischen „Standard“ und „Extragroß“?
15,87%
bei 210g
3) In einer Bäckerei weiß man aus Erfahrung, dass die Menge der täglich verkauften Semmeln
normalverteilt ist mit μ=245 und σ=6.
a) Wie groß ist die Wahrscheinlichkeit, dass an einem Tag zwischen 237 und 250 Semmeln
verkauft werden?
74,34%
b) An einem Tag hat der Bäcker 255 Semmeln gefertigt.
Mit welcher Wahrscheinlichkeit kommt er in Schwierigkeiten?
5,71%
c) In welchem um den Erwartungswert symmetrischen Bereich liegt mit 98%iger
Wahrscheinlichkeit die Anzahl der verkauften Semmeln?
(Rechne jeweils mit Stetigkeitskorrektur)
[231;259]