Serie 7

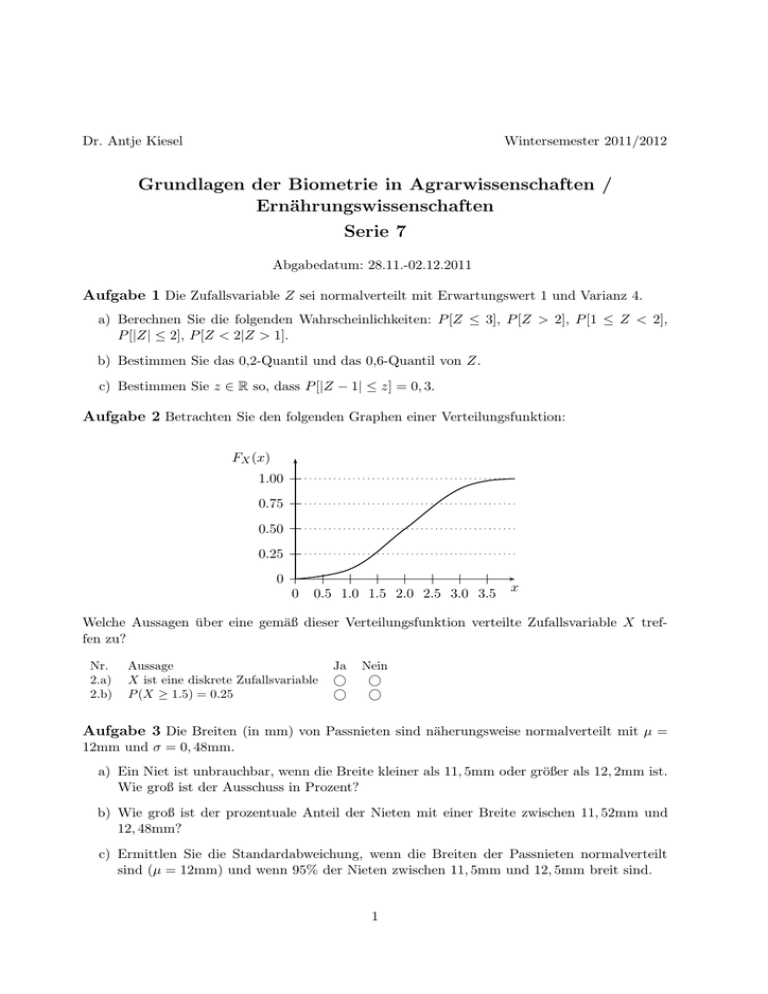
Dr. Antje Kiesel
Wintersemester 2011/2012
Grundlagen der Biometrie in Agrarwissenschaften /
Ernährungswissenschaften
Serie 7
Abgabedatum: 28.11.-02.12.2011
Aufgabe 1 Die Zufallsvariable Z sei normalverteilt mit Erwartungswert 1 und Varianz 4.
a) Berechnen Sie die folgenden Wahrscheinlichkeiten: P [Z ≤ 3], P [Z > 2], P [1 ≤ Z < 2],
P [|Z| ≤ 2], P [Z < 2|Z > 1].
b) Bestimmen Sie das 0,2-Quantil und das 0,6-Quantil von Z.
c) Bestimmen Sie z ∈ R so, dass P [|Z − 1| ≤ z] = 0, 3.
Aufgabe 2 Betrachten Sie den folgenden Graphen einer Verteilungsfunktion:
FX (x)
1.00
0.75
0.50
0.25
0
0
0.5 1.0 1.5 2.0 2.5 3.0 3.5
x
Welche Aussagen über eine gemäß dieser Verteilungsfunktion verteilte Zufallsvariable X treffen zu?
Nr.
2.a)
2.b)
Aussage
X ist eine diskrete Zufallsvariable
P (X ≥ 1.5) = 0.25
Ja
Nein
Aufgabe 3 Die Breiten (in mm) von Passnieten sind näherungsweise normalverteilt mit µ =
12mm und σ = 0, 48mm.
a) Ein Niet ist unbrauchbar, wenn die Breite kleiner als 11, 5mm oder größer als 12, 2mm ist.
Wie groß ist der Ausschuss in Prozent?
b) Wie groß ist der prozentuale Anteil der Nieten mit einer Breite zwischen 11, 52mm und
12, 48mm?
c) Ermittlen Sie die Standardabweichung, wenn die Breiten der Passnieten normalverteilt
sind (µ = 12mm) und wenn 95% der Nieten zwischen 11, 5mm und 12, 5mm breit sind.
1
Aufgabe 4 Die Zufallsvariable X habe die Varianz 1/4.
a) Schätzen Sie P [|X − E[X]| > 1] mit der Tschebyscheff-Ungleichung nach oben ab.
b) Berechnen Sie diese Wahrscheinlichkeit für den Fall, dass X
1. Poisson-verteilt
2. exponentialverteilt
3. normalverteilt
ist, und vergleichen Sie die Werte mit dem in a) erzielten Ergebnis.
2