Halos Dunkler Materie - Physikalischer Verein

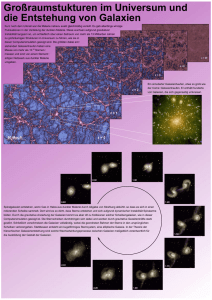
Kosmogonie
Das dunkle Zeitalter
Von der Rekombination
bis zu den
ersten Sternen
Temperatur- und Dichteverlauf
10100
PlanckAera
GUTAera
QuarkAera
Hadron LeptonAera
Aera
1080
WIMPS
entstehen
StrahlungsAera
MaterieAera
WIMPS
entkoppeln
1060
Dichte
1040
Nukleosynthese
[g/cm3]
1020
Temperatur [K]
1
Rekombination
10-20
10-40
10-50
Inflation
heute
10-40
10-30
10-20
© Dr. R. Göhring
10-10
[email protected]
1
1010
1020
V-2
Dunkle Materie
• Hot dark matter HDM
– Besteht aus (hypothetischen) Teilchen, die sich mit einer
Geschwindigkeit nahe Lichtgeschwindigkeit bewegen.
– Kandidaten wären z.B. die Neutrinos.
– Es zeigt sich, daß mit der HDM die Strukturbildung im
Universum nicht in der Form möglich ist, wie wir sie kennen.
• Cold dark matter CDM
– Besteht aus den (hypothetischen) schweren WIMPS.
– Nach der ihrer Entkopplung von der Materie und Strahlung
bestimmen die Fluktuationen der kalten Dunklen Materie die
Dichteverteilung im frühen Universum.
– Nur mit CDM kann die Strukturbildung sinnvoll erklärt werden.
© Dr. R. Göhring
[email protected]
V-3
Dichte des Universums
Dichte des Universums [g cm-3]
1010
strahlungsdominiert
1
materiedominiert
Strahlung
10-10
Materie
Rekombination
10-20
10-30
sec
10-40
1
102
104
106
108
© Dr. R. Göhring
1010
1012
ca. 100.000 a
[email protected]
1014
1016
heute
1018
V-4
Dichtefluktuation d
• Dichtefluktuationen entstehen bereits ganz zu Beginn in der
Planck-Äre aufgrund quantenmechanischer Effekte.
• Nach der Entkopplung der CDM sind diese
Dichtefluktuationen im Wesentlichen solche der Dunklen
Materie.
• Die Dichtefluktuation der Baryonen unterscheidet sich vor
der Rekombination von der der CDM:
– Zu Beginn des materiedominierten Universums ist die Dichte
der Strahlung nach wie vor größer als die der baryonischen
Materie.
– Durch die Wechselwirkung der Strahlung mit der Materie wird
die Fluktuation der Materiedichte „geglättet“.
– Erst nach der Rekombination wird die Verteilung der Baryonen
ähnlich der der Dunklen Materie.
© Dr. R. Göhring
[email protected]
V-5
Plasma-Schwingungen
•
In dem Plasma existieren
Dichteschwankungen verursacht
durch Quantenfluktuationen in der
Frühphase kurz nach dem Urknall.
•
Das Plasma – die baryonische
Materie – gerät dadurch in
Schwingungen.
•
Die Schwingung breitet sich mit
der Schallgeschwindigkeit vc des
Plasmas aus:
vc 
3
 0,6  c
•
Es können nur Plasmawolken
schwingen, die in den 380.000
Jahren mindestens einmal von
einer Schallwelle durchlaufen
wurden
Schallhorizont Ls ≈ 240.000 Lj
•
Ls ist die „Grundschwingung“ in
der Hintergrundstrahlung.
http://background.uchicago.edu/
© Dr. R. Göhring
c
[email protected]
V-6
Winkel des Schallhorizonte
• Unter welchem Winkel α sehen wir heute –
nach etwa 13,7 Milliarden Jahren – den
Schallhorizont Ls ≈ 240.000 Lj?
Ls
• Der Zeitpunkt, als das Universum
durchsichtig wurde und die
Hintergrundstrahlung entstand, entspricht
einer Rotverschiebung
z ≈ 1000
Ls
Ls
• Durch die Expansion des Universums hat
sich der damalige Schallhorizont
ausgedehnt:
Ls(heute) = (1+z)·Ls
Ls(heute) ≈ 2,4·108 Lj
• Wenn das Universum flach ist, muß der
Winkel α sich ergeben zu
α = (2,4·108)/(13,7·109) ≈ 0,018
α ≈ 1o
© Dr. R. Göhring
[email protected]
V-7
Powerspektrum
© Dr. R. Göhring
[email protected]
V-8
http://map.gsfc.nasa.gov/m_ig/030639/bentspace1.jpg
Einfluß der Krümmung K
http://background.uchicago.edu/
© Dr. R. Göhring
[email protected]
V-10
Strukturbildung nach der Rekombination
• Baryonen und Strahlung sind entkoppelt mit der Folge, daß
die Interaktion zwischen Photonen und Baryonen seltener
werden.
• Baryonen können daher in den Potentialtopf der Dunklen
Materie „fallen“ und die Verteilung von Baryonen und
Dunkler Materie wird sehr ähnlich.
• Diese Potentialtöpfe sind die Geburtsstätten der ersten
Sterne und in der Folge der Galaxien.
© Dr. R. Göhring
[email protected]
V-11
Dichtefluktuation
r(r,tx)
r
r
d(r, t x ) 
r(r, t x )  r(t x )
r(t x )
Wie entwickeln sich die Dichtefluktuationen mit der Expansion
des Universums ??
© Dr. R. Göhring
[email protected]
V-12
Gravitative Instabilität
• Ein überdichtes Gebiet mit Dr > 0, d.h. auch d > 0, erzeugt ein
stärkeres Gravitationsfeld als im kosmischen Mittel.
• Durch diese Selbstgravitation expandiert das Gebiet langsamer als
die mittlere Hubble-Expansion.
• Durch die verlangsamte Expansion nimmt die Dichte langsamer ab
als im kosmischen Mittel (~ a-3(t)r0) mit der Folge, daß der
Dichtekontrast dort ansteigt.
• Damit steigt wieder die relative Dichte und diese erzeugt ein noch
stärkeres Gravitationsfeld ……
• Umgekehrt verläuft der Prozeß in unterdichten (d < 0) Regionen.
• Die gravitative Instabilität führt zu einem Anwachsen der
Dichtefluktuationen.
© Dr. R. Göhring
[email protected]
V-13
Heutige Dichtefluktuation rückgerechnet
• Heutige Dichtefluktuation auf Skalen der Superhaufen
(~10 Mpc): d ~ 1.
• Zum Zeitpunkt der Rekombination (z ≈ 1000) müßte
demnach d ≥ 10-3 betragen haben.
• In ähnlicher Größenordnung müßte dann auch die
Temperaturfluktuation gelegen haben: DT/T ≥ 10-3.
Beobachtet wird aber DT/T ~ 10-5.
• Das spricht für die Dominanz der Dunklen Materie, die
einen größeren Dichtekontrast (unterhalb ~1o) hat und
Potentialtöpfe bilden kann, in die die Baryonen nach der
Rekombination hineinfallen können.
© Dr. R. Göhring
[email protected]
V-14
Abkopplung der dichteren Bereiche von der Expansion
(Violent Relaxation)
• Stellen wir uns einen kugelförmigen Bereich dunkler Materie vor
mit einer Überdichte d > 0 gegenüber der Umgebung mit der
mittleren Dichte.
• Wegen höheren Gravitation expandiert die Kugel langsamer als
das Universum als Ganzes mit der Folge, daß der Dichtekontrast
weiter erhöht wird.
• Die Expansionsgleichung der Kugel ist die gleiche FriedmannGleichung wie für das übrige Universum, mit dem Unterschied,
daß der Bereich eine größere Masse besitzt.
• Hat die Kugel eine entsprechend große Masse, dann kommt die
Expansion bei einem maximalen Radius zum Stillstand und
kollabiert dann.
• Die Dunkle Materie fällt nicht radial zusammen, sondern streut an
lokalen Dichteschwankungen und „virialisiert“, d.h. bildet lokale
Verdichtungen.
© Dr. R. Göhring
[email protected]
V-15
Sphärischer Kollaps


d
a(t)  H0  m   m  L  1  a2 (t)   L 
dt
 a(t)

• Den quantitativen Verlauf der
Expansion des Universums
mit dem LCDM-Modell zeigt
die blaue Kurve.
a(t)
1
 M=0,3;  L=0,7
200· M;  L=0,7
0.8
• Für einen Bereich mit der
Dichte von 200·M zeigt die
rote Kurve, wie er sich von
der allgemeinen Expansion
abkoppelt und
0.6
0.4
• schließlich kollabiert.
• Dies sind die
0.2
0
1
2
Halos Dunkler Materie
t
0
0.2
0.4
0.6
0.8
heute
• Sie sind die Geburtsstätten
der Sterne und Galaxien.
© Dr. R. Göhring
[email protected]
V-16
Bottom-up Szenario
• Die Masse eines Halos Dunkler Materie muß eine Grenzgröße
überschreiten, damit das Gas einströmen kann.
• Diese Grenzmasse ist die Jeans-Masse MJ; sie definiert die minimale
Masse eines Halos für den gravitativen Einfall des Gases:
3/2
5/2  c2s 
M  MJ 
 
6 G

1
r

T3
r
• cs ist die Schallgeschwindigkeit in dem Gas, und G die Gravitationskonstante.
• Solch ein Halo Dunkler Materie hat eine Masse von ~106 M. Er ist
die Voraussetzung für die Bildung erster Sterne.
• Bottom-up Szenario: Es bilden sich zuerst kleine Halos Dunkler
Materie, die durch Vereinigung größere bilden.
© Dr. R. Göhring
[email protected]
V-17
Millenium-Simulation
• Numerische Simulation von „Teilchen Dunkler Materie“ für einen
Ausschnitt des Universums 2005 durchgeführt am Max-PlanckInstitut für Astrophysik in Garching (V. Springel et.al.)
– Kosmologisches Modell: LCDM mit m = 0,25, L = 0,75,
Hubble-Konstante = 100·h mit h = 0,73.
– Kantenlänge des Würfels = 500h-1 Mpc (= 685 Mpc).
– Anzahl der „Teilchen“: (2160)3 ≈ 1010.
– Masse der „Teilchen Dunkler Materie“: 8,6·108h-1 M.
– Räumliche Auflösung ~5h-1 kpc (≈ 22.000 Lj ≈ 1/5 Durchmesser der
Milchstraße)
– Dauer: 28 Tage Rechenzeit auf einer IBM p690 mit 512 Prozessoren
(~0,2 TFlops).
• Das Ergebnis der Simulation sind die Positionen und die
Geschwindigkeiten der ~109 „Teilchen“ in Abhängigkeit von der
Rotverschiebung z; von z = 127 bis z = 0 (heute).
• Die Analyse dieser gigantischen Datenmenge ist mindestens so
aufwendig wie die Simulation selbst.
© Dr. R. Göhring
[email protected]
V-18
Quelle: Springel, V. et al. 2005, astro-ph/0504097
Millenium-Simulation: Ergebnisse
1
• Die Anfangsbedingungen für die Simulation
werden für sehr große „z“, d.h. große
Rotverschiebungen, festgelegt.
• Die „Teilchen“ der Dunklen Materie werden in
dem zu simulierenden Raumausschnitt so
verteilt, daß ihre Dichtefluktuation (oder das
entsprechende Leistungsspektrum) dem
theoretisch bekannten entspricht.
2
• Die sich aus der Simulation ergebenden
Informationen über die Positionen und
Geschwindigkeiten können dann z.B. nach den
Gesichtspunkten ausgewertet werden:
– Betrachtung unter dem Aspekt unterschiedlicher
räumlicher Auflösung (zoom in; Film 1) oder
– als Entwicklung der Strukturen in Abhängigkeit
von der Zeit resp. der Rotverschiebung (Film 2).
Quelle: http://www.mpa-garching.mpg.de/galform/data_vis/index.shtml
© Dr. R. Göhring
[email protected]
V-20
Millenium-Simulation: Statistische Aussagen
© Dr. R. Göhring
•
Mit den Auswertungen der
Simulation lassen sich nur
statistische Aussagen
treffen.
•
Es kann demnach kein
Ergebnis der Simulation
sein, daß z.B. in genau 2,7
Mio. Lichtjahren Entfernung
von unserer Galaxie sich
eine andere befindet, die
genau der AndromedaGalaxie entspricht.
•
Es sind nur statistische
Aussagen in der Form der
mittleren Dichtefluktuation
sinnvoll
[email protected]
V-21
Quelle:http://www.mso.anu.edu.au/2dFGRS/
© Dr. R. Göhring
[email protected]
V-22
Bildung von Galaxien
Baryonische Materie strömt in Halos Dunkler Materie ein; Galaxien können
sich aber nur dort bilden, wo das Dichtefeld einen kritischen Wert dc überschreitet (blaue gepunktete Bereiche).
d
dc
x
Man kann daher erwarten, daß die Verteilung der Galaxien im Universum
korreliert ist mit der Verteilung der Dunklen Materie.
© Dr. R. Göhring
[email protected]
V-23
Gas und Dunkle Materie
Quelle: http://www.mpa-garching.mpg.de/galform/data_vis/index.shtml
•
Die Simulation beschreibt die Entwicklung
der Dunklen Materie in Abhängigkeit von
der Zeit resp. der Rotverschiebung z.
•
Wesentlich ist dabei die Bildung der Halos
Dunkler Materie und deren Verschmelzung.
•
Das Gas – die baryonische Materie – folgt
zunächst der Dunklen Materie. Wenn aber
das Gas dicht genug ist, spielen andere
physikalische Prozesse eine Rolle –
Heizung, Kühlung, Reibung etc. –, denen
die Dunkle Materie nicht unterworfen ist.
•
Diese Prozesse müssen mit anderen
Methoden simuliert werden.
•
Die Verteilung der „leuchtenden“ Materie
folgt aber weitgehend der Verteilung der
Dunklen Materie.
© Dr. R. Göhring
[email protected]
V-24
Galaxien und Dunkle Materie
• Linke Spalte der Abb. zeigt
einen der massereichsten Halos
der Millennium-Simulation zu
verschiedenen Zeiten der
Entwicklung – bei z = 6,2 und
heute (z = 0).
• In der rechten Spalte werden die
zu diesen Zeiten vorhandenen
Galaxien in diesem Halo
dargestellt.
• Im oberen – zu dem frühen
Zeitpunkt – verdeutlichen die
blauen Punkte Galaxien mit
jungen, heißen Sternen der
Population III.
Quelle: Springel, V. et al. 2005, astro-ph/0504097
© Dr. R. Göhring
[email protected]
• Im unteren – heute – existieren
zahlreiche Galaxien mit metallreichen Sternen der Population I
und II, erkennbar an den roten
Punkten.
V-25
Statistische Befunde
• Der Vergleich statistischer
Untersuchungen von Beobachtungen
und Ergebnisse der MillenniumSimulation zeigen überzeugende
Übereinstimmungen.
• Die roten Punkte zeigen die
Messungen der 2-Punkt-Korrelation
modellierter Galaxien zum heutigen
Zeitpunkt (vergleichbar mit der
mittleren Dichtefluktuation).
• Die blauen Punkte sind die
Ergebnisse an konkreten,
beobachteten Galaxien (2dFGRS).
Quelle: Springel, V. et al. 2005, astro-ph/0504097
© Dr. R. Göhring
• Die gestrichelte Linie gibt die
Korrelationsfunktion der Dunklen
Materie wieder.
[email protected]
V-26
Erste Sterne
•
Die Entstehung erster kompakter Objekte in dem Gemisch aus im
wesentlichen Wasserstoff, Helium sowie Halos Dunkler Materie ca. 30 Mio.
Jahre nach dem Urknall (z ~ 65) bildete den entscheidenden Übergang
von der ursprünglichen „Einförmigkeit“ zur heutigen komplexen Struktur
dar.
•
Molekularer Wasserstoff – H2 – ermöglichte, daß die kollabierenden
Wolken aus Gas (Masse 105 – 106 M) soweit abkühlen konnten, daß sich
Sterne bilden konnten
– bestehend fast ausschließlich aus Wasserstoff und Helium und
– mit einer Masse von ~100 M und damit
– eine extrem kurze Lebensdauer von 2 – 3 Millionen Jahren.
•
Die Strahlung des jungen Sterns bewirkt, daß der molekulare Wasserstoff
in der Umgebung dissoziiert und der Wasserstoff ionisiert wird.
•
Die Supernova-Explosion sorgt dann dafür, daß das Gas in dem Halo mit
höheren Elementen – z.B. Kohlenstoff und Sauerstoff – angereichert
wurde und so Sterne der 2. Generation – Population III Sterne – gebildet
wurden, langlebige Sterne, die ggf. heute noch beobachtet werden
können.
© Dr. R. Göhring
[email protected]
V-27
Reionisation
Quelle: Loeb, A., 2008, astro-ph/0804.2258v1
Kühlung von atomarem Wasserstoff und Helium kann nur in Halos mit einer Masse über ~108
M erfolgen, wo das einfallende Gas aufgeheizt wird auf über 10.000 K. Diese bildeten sich bei
einer Rotverschiebung um z = 45, entspr. einem Weltalter von ca. 50 Mio. Jahre. Damit
beginnt die vollständige Reionisation und die weitere Aufheizung des intergalaktischen
Mediums über 10.000 K.
Bei diesen Temperaturen kann in dem Gas erst wieder in Halos mit einer Masse von mehr als
~109 M eine Sternbildung erfolgen. Erste Halos von der Größenordnung unserer Milchstraße
M = 1012 M bilden sich dann bei einem Weltalter von 400 Mio. Jahren (z ≈ 12).
© Dr. R. Göhring
[email protected]
V-28