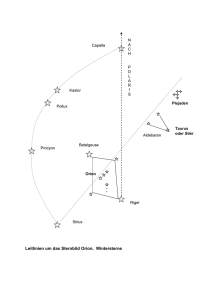
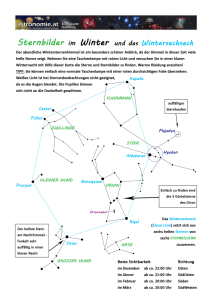
3. Schriftliche Wiederholung aus Physik Donnerstag, 27. Februar 1997
Werbung

4. Lernzielkontrolle aus Physik 2 ak – 2016 - kircher Mittwoch 4. Juni 2013 Gruppe A ACHTUNG: Fehlerhafte und unübliche Notation sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) Das Raumschiff Orion fliegt mit 0,8c von der Erde in das 16 ly entfernte System Krakatau. Beim Start sind alle Uhren (auf der Erde, auf Krakatau und auf Orion synchronisiert, d.h. alle Kalender zeigen das gleiche Datum). Orion startet am 31. Dezember 2040. Berechnen Sie, welches Datum (nur das Kalenderjahr muss angegeben werden) die Kalender in Orion, auf Krakatau und auf der Erde bei der Landung von Orion auf Krakatau zeigen 16 ly;0 1–0 2 = 20 a torion = 20 8 = 20 · 0,6 = 12 a 8c Die Kalender auf Erde und Krakatau zeigen 2060, Kalender auf Orion 2052. terde = b) 2. a) b) Raumschiff Orion fliegt von der Erde in das 16 ly entfernte System Krakatau. Der Lichtjahreszähler in Orion zeigt bei der Landung jedoch nur eine zurückgelegte Strecke von 12,8 ly an. Berechnen Sie die Geschwindigkeit mit der Orion unterwegs war. 12,8 = 16 1 – u2 u = 0,6 Orion war mit 60 % der Lichtgeschwindigkeit unterwegs Berechnen Sie, um welchen Prozentsatz sich die Masse eines Körpers ändert, wenn er sich mit 70 % der Lichtgeschwindigkeit bewegt. md = Error! md = 1,40 m0 Die Masse eines Körpers mit der Geschwindigkeit 0,7c ist 40 % höher als die Ruhemasse. In einem Experiment werden Teilchen mit der Geschwindigkeit von 10 % der Lichtgeschwindigkeit durch eine Messstrecke geschickt. Klassisch würde man eine Laufzeit von 5 ns erwarten. Berechnen Sie die tatsächliche Laufzeit dieser Teilchen. Argumentieren Sie, ob dieser Effekt mit einer Uhr, die eine Messgenauigkeit von 1 % hat, nachgewiesen werden kann. 1–0 2 tb = 5 ns 1 = 4,97 ns d.i. eine Fehler von 0,6 % also weniger als die Messungenauigkeit der Uhr, d.h. kann nachgewiesen werden. 3. a) Teilchen mit einer Halbwertszeit von 4 ns durchlaufen eine Strecke von 6 m mit einer Geschwindigkeit von 0,99c. Berechnen Sie den Anteil der Teilchen, die am Ende der Laufzeit noch vorhanden sind. Berechnen Sie diesen Anteil klassisch und relativistisch. 6 m;0 ta = = 20 ns = 5 HWZ Anteil klassisch = 0,55 = 3 % 99 · 3 · 108 m/s tb = 5 HWZ · b) 4. a) b) 1–0 992 = 0,71 HWZ Anteil relativistisch = 0,50,71 = 61,3 % In einem Teilchenbeschleuniger laufen zwei Teilchen mit den Geschwindigkeiten 0,9c aufeinander zu (Geschwindigkeiten relativ zum Labor). Berechnen Sie die Relativgeschwindigkeit dieser Teilchen zueinander. w = Error! = 0,994 also 99,4 % der Lichtgeschwindigkeit Berechnen Sie die Geschwindigkeit eines Körpers, dessen dynamische Masse um 30 % höher ist als seine Ruhemasse ist. 1,3 m0 = Error! 1,69 (1 – 2) = 1 1 – 2 = 0,591 2 = 0,409 = 0,64 v = 0,64c Fr. Huber lebt im Einsteinland (Lichtgeschwindigkeit hier c = 100 km/h). Sie fährt mit ihrem Auto aus dem Stand los und kann relativ zügig auf 50 km/h beschleunigen. Später fährt sie 95 km/h auf der Autobahn und möchte das Fahrzeug vor ihr überholen und auf 100 km/h beschleunigen. Kreuzen Sie die zutreffenden Aussagen an: Fr. Huber kann noch so sehr auf’s Gas steigen, das Auto beschleunigt kaum noch, weil die X dynamische Masse jetzt viel höher ist. Das Fahrzeug beschleunigt genau gleich wie bei 0 km/h, weil die Motorleistung natürlich gleich hoch ist. Fr. Huber kann gar nicht mehr beschleunigen, weil 95 km/h hier fast so groß wie die Lichtgeschwindigkeit ist. Fr. Huber wird 100 km/h nie erreichen, weil bei v = c die dynamische Masse unendlich groß X wird. 4. Lernzielkontrolle aus Physik 2 ak – 2016 - kircher Mittwoch 4. Juni 2013 Gruppe B ACHTUNG: Fehlerhafte und unübliche Notation sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) Das Raumschiff Orion fliegt mit 0,8c von der Erde in das 24 ly entfernte System Krakatau. Beim Start sind alle Uhren (auf der Erde, auf Krakatau und auf Orion synchronisiert, d.h. alle Kalender zeigen das gleiche Datum). Orion startet am 31. Dezember 2040. Berechnen Sie, welches Datum (nur das Kalenderjahr muss angegeben werden) die Kalender in Orion, auf Krakatau und auf der Erde bei der Landung von Orion auf Krakatau zeigen 24 ly;0 1–0 2 = 30 a torion = 30 8 = 30 · 0,6 = 18 a 8c Die Kalender auf Erde und Krakatau zeigen 2070, Kalender auf Orion 2058. terde = b) 2. a) b) Raumschiff Orion fliegt von der Erde in das 24 ly entfernte System Krakatau. Der Lichtjahreszähler in Orion zeigt bei der Landung jedoch nur eine zurückgelegte Strecke von 14,4 ly an. Berechnen Sie die Geschwindigkeit mit der Orion unterwegs war. 14,4 = 24 1 – u2 u = 0,8 Orion war mit 80 % der Lichtgeschwindigkeit unterwegs Berechnen Sie, um welchen Prozentsatz sich die Masse eines Körpers ändert, wenn er sich mit 60 % der Lichtgeschwindigkeit bewegt. md = Error! md = 1,25 m0 Die Masse eines Körpers mit der Geschwindigkeit 0,6c ist 25 % höher als die Ruhemasse. In einem Experiment werden Teilchen mit der Geschwindigkeit von 10 % der Lichtgeschwindigkeit durch eine Messstrecke geschickt. Klassisch würde man eine Laufzeit von 5 ns erwarten. Berechnen Sie die tatsächliche Laufzeit dieser Teilchen. Argumentieren Sie, ob dieser Effekt mit einer Uhr, die eine Messgenauigkeit von 2 % hat, nachgewiesen werden kann. 1–0 2 tb = 5 ns 1 = 4,97 ns d.i. eine Fehler von 1,6 % also weniger als die Messungenauigkeit der Uhr, d.h. kann nicht nachgewiesen werden. 3. a) Teilchen mit einer Halbwertszeit von 4 ns durchlaufen eine Strecke von 6 m mit einer Geschwindigkeit von 0,99c. Berechnen Sie den Anteil der Teilchen, die am Ende der Laufzeit noch vorhanden sind. Berechnen Sie diesen Anteil klassisch und relativistisch. 6 m;0 ta = = 20 ns = 5 HWZ Anteil klassisch = 0,55 = 3 % 99 · 3 · 108 m/s tb = 5 HWZ · b) 4. a) b) 1–0 992 = 0,71 HWZ Anteil relativistisch = 0,50,71 = 61,3 % In einem Teilchenbeschleuniger laufen zwei Teilchen mit den Geschwindigkeiten 0,8c aufeinander zu (Geschwindigkeiten relativ zum Labor). Berechnen Sie die Relativgeschwindigkeit dieser Teilchen zueinander. w = Error! = 0,976 also 97,6 % der Lichtgeschwindigkeit Berechnen Sie die Geschwindigkeit eines Körpers, dessen dynamische Masse um 30 % höher ist als seine Ruhemasse ist. 1,3 m0 = Error! 1,69 (1 – 2) = 1 1 – 2 = 0,591 2 = 0,409 = 0,64 v = 0,64c Fr. Huber lebt im Einsteinland (Lichtgeschwindigkeit hier c = 100 km/h). Sie fährt mit ihrem Auto aus dem Stand los und kann relativ zügig auf 50 km/h beschleunigen. Später fährt sie 95 km/h auf der Autobahn und möchte das Fahrzeug vor ihr überholen und auf 100 km/h beschleunigen. Kreuzen Sie die zutreffenden Aussagen an: Das Fahrzeug beschleunigt genau gleich wie bei 0 km/h, weil die Motorleistung natürlich gleich hoch ist. Fr. Huber kann gar nicht mehr beschleunigen, weil 95 km/h hier fast so groß wie die Lichtgeschwindigkeit ist. Fr. Huber wird 100 km/h nie erreichen, weil bei v = c die dynamische Masse unendlich groß X wird. Fr. Huber kann noch so sehr auf’s Gas steigen, das Auto beschleunigt kaum noch, weil die X dynamische Masse jetzt viel höher ist. 4. Lernzielkontrolle aus Physik 2 ak – 2016 - kircher Mittwoch 4. Juni 2013 Gruppe A ACHTUNG: Fehlerhafte und unübliche Notation sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. 2. 3. 4. a) Das Raumschiff Orion fliegt mit 0,8c von der Erde in das 16 ly entfernte System Krakatau. Beim Start sind alle Uhren (auf der Erde, auf Krakatau und auf Orion synchronisiert, d.h. alle Kalender zeigen das gleiche Datum). Orion startet am 31. Dezember 2040. Berechnen Sie, welches Datum (nur das Kalenderjahr muss angegeben werden) die Kalender in Orion, auf Krakatau und auf der Erde bei der Landung von Orion auf Krakatau zeigen b) Raumschiff Orion fliegt von der Erde in das 16 ly entfernte System Krakatau. Der Lichtjahreszähler in Orion zeigt bei der Landung jedoch nur eine zurückgelegte Strecke von 12,8 ly an. Berechnen Sie die Geschwindigkeit mit der Orion unterwegs war. a) Berechnen Sie, um welchen Prozentsatz sich die Masse eines Körpers ändert, wenn er sich mit 70 % der Lichtgeschwindigkeit bewegt. b) In einem Experiment werden Teilchen mit der Geschwindigkeit von 10 % der Lichtgeschwindigkeit durch eine Messstrecke geschickt. Klassisch würde man eine Laufzeit von 5 ns erwarten. Berechnen Sie die tatsächliche Laufzeit dieser Teilchen. Argumentieren Sie, ob dieser Effekt mit einer Uhr, die eine Messgenauigkeit von 1 % hat, nachgewiesen werden kann. a) Teilchen mit einer Halbwertszeit von 4 ns durchlaufen eine Strecke von 6 m mit einer Geschwindigkeit von 0,99c. Berechnen Sie den Anteil der Teilchen, die am Ende der Laufzeit noch vorhanden sind. Berechnen Sie diesen Anteil klassisch und relativistisch. b) In einem Teilchenbeschleuniger laufen zwei Teilchen mit den Geschwindigkeiten 0,9c aufeinander zu (Geschwindigkeiten relativ zum Labor). Berechnen Sie die Relativgeschwindigkeit dieser Teilchen zueinander. a) Berechnen Sie die Geschwindigkeit eines Körpers, dessen dynamische Masse um 30 % höher ist als seine Ruhemasse ist. b) Fr. Huber lebt im Einsteinland (Lichtgeschwindigkeit hier c = 100 km/h). Sie fährt mit ihrem Auto aus dem Stand los und kann relativ zügig auf 50 km/h beschleunigen. Später fährt sie 95 km/h auf der Autobahn und möchte das Fahrzeug vor ihr überholen und auf 100 km/h beschleunigen. Kreuzen Sie die zutreffenden Aussagen an: Fr. Huber kann noch so sehr auf’s Gas steigen, das Auto beschleunigt kaum noch, weil die dynamische Masse jetzt viel höher ist. Das Fahrzeug beschleunigt genau gleich wie bei 0 km/h, weil die Motorleistung natürlich gleich hoch ist. Fr. Huber kann gar nicht mehr beschleunigen, weil 95 km/h hier fast so groß wie die Lichtgeschwindigkeit ist. Fr. Huber wird 100 km/h nie erreichen, weil bei v = c die dynamische Masse unendlich groß wird. 4. Lernzielkontrolle aus Physik 2 ak – 2016 - kircher Mittwoch 4. Juni 2013 Gruppe B ACHTUNG: Fehlerhafte und unübliche Notation sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. 2. 3. 4. a) Das Raumschiff Orion fliegt mit 0,8c von der Erde in das 24 ly entfernte System Krakatau. Beim Start sind alle Uhren (auf der Erde, auf Krakatau und auf Orion synchronisiert, d.h. alle Kalender zeigen das gleiche Datum). Orion startet am 31. Dezember 2040. Berechnen Sie, welches Datum (nur das Kalenderjahr muss angegeben werden) die Kalender in Orion, auf Krakatau und auf der Erde bei der Landung von Orion auf Krakatau zeigen b) Raumschiff Orion fliegt von der Erde in das 24 ly entfernte System Krakatau. Der Lichtjahreszähler in Orion zeigt bei der Landung jedoch nur eine zurückgelegte Strecke von 14,4 ly an. Berechnen Sie die Geschwindigkeit mit der Orion unterwegs war. a) Berechnen Sie, um welchen Prozentsatz sich die Masse eines Körpers ändert, wenn er sich mit 60 % der Lichtgeschwindigkeit bewegt. b) In einem Experiment werden Teilchen mit der Geschwindigkeit von 10 % der Lichtgeschwindigkeit durch eine Messstrecke geschickt. Klassisch würde man eine Laufzeit von 5 ns erwarten. Berechnen Sie die tatsächliche Laufzeit dieser Teilchen. Argumentieren Sie, ob dieser Effekt mit einer Uhr, die eine Messgenauigkeit von 2 % hat, nachgewiesen werden kann. a) Teilchen mit einer Halbwertszeit von 4 ns durchlaufen eine Strecke von 6 m mit einer Geschwindigkeit von 0,99c. Berechnen Sie den Anteil der Teilchen, die am Ende der Laufzeit noch vorhanden sind. Berechnen Sie diesen Anteil klassisch und relativistisch. b) In einem Teilchenbeschleuniger laufen zwei Teilchen mit den Geschwindigkeiten 0,8c aufeinander zu (Geschwindigkeiten relativ zum Labor). Berechnen Sie die Relativgeschwindigkeit dieser Teilchen zueinander. a) Berechnen Sie die Geschwindigkeit eines Körpers, dessen dynamische Masse um 30 % höher ist als seine Ruhemasse ist. b) Fr. Huber lebt im Einsteinland (Lichtgeschwindigkeit hier c = 100 km/h). Sie fährt mit ihrem Auto aus dem Stand los und kann relativ zügig auf 50 km/h beschleunigen. Später fährt sie 95 km/h auf der Autobahn und möchte das Fahrzeug vor ihr überholen und auf 100 km/h beschleunigen. Kreuzen Sie die zutreffenden Aussagen an: Das Fahrzeug beschleunigt genau gleich wie bei 0 km/h, weil die Motorleistung natürlich gleich hoch ist. Fr. Huber kann gar nicht mehr beschleunigen, weil 95 km/h hier fast so groß wie die Lichtgeschwindigkeit ist. Fr. Huber wird 100 km/h nie erreichen, weil bei v = c die dynamische Masse unendlich groß wird. Fr. Huber kann noch so sehr auf’s Gas steigen, das Auto beschleunigt kaum noch, weil die dynamische Masse jetzt viel höher ist.